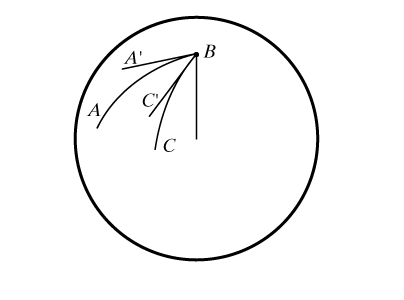- Сферические треугольники.
- Свойства сферических треугольников.
- Сфера из двух треугольников
- Математика процесса
- Техническая часть
- Увеличиваем разрешение
- Наклон
- СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ
- Основные положения сферической геометрии.
- Прямые, отрезки, расстояния и углы на сфере.
- Сферический треугольник.
- Координаты на сфере.
- 🔥 Видео
Сферические треугольники.

Свойства сферических треугольников.
Каждая сторона и угол сферического треугольника по определению меньше 180°. Геометрия на поверхности шара является неевклидовой; в каждом сферическом треугольнике сумма сторон заключена между 0 и 360°, сумма углов заключена между 180° и 540°. В каждом сферическом треугольнике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180° плюс третий угол.
Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):
- тремя сторонами,
- тремя углами,
- двумя сторонами и заключенным между ними углом,
- стороной и двумя прилежащими к ней углами.
Видео:Как нарисовать ШАР (сфера). Построение , штриховка.Скачать

Сфера из двух треугольников

И вот, однажды, когда меня мучила бессонница, я решил попробовать совместить эти два подхода: нарисовать вращающуюся сферу (с натянутой на неё картой планеты) через OpenGL, но при этом оставив её плоской.
И должен сказать, что у меня это получилось. Но обо всём по порядку.
Математика процесса
Для начала определимся с собственно задачей. Для каждой точки на экране у нас имеются две экранные координаты в декартовой системе координат, и нам необходимо найти для неё сферические координаты (фактически, широту и долготу), которые по сути и являются текстурными координатами для карты планеты.
Итак. Переход от сферической системы координат к декартовой задаётся системой уравнений (взято с Википедии):
а обратный переход — такими уравнениями:
Координату Z мы легко можем получить из X и Y, зная радиус, а сам радиус мы можем принять равным единице.
В дальнейшем договоримся о том, что приведённые выше уравнения мы слегка изменим, поменяв местами понятия Y (у нас это будет экранная вертикаль) и Z (это будет глубина сцены).
Техническая часть
Реализация идеи потребует от нас применения квада (я уже писал о том, как его использовать, поэтому повторяться не буду, тем более что ниже приведена ссылка на полный исходный код проекта), а также двух текстур: собственно карты планеты (я использовал текстуру Земли размера 2048×1024) и карты текстурных координат. Код генерации второй текстуры аккуратно повторяет математику преобразования из декартовых координат в сферические:
Отметим, что координаты X и Y переводятся из диапазона [0..texSize] в диапазон [-1..1], а текстурные координаты U и V переводятся из радианов в диапазон [0..255], после чего записываются соответственно в красную и зелёную компоненты 32-битной текстуры. Альфа-канал используется для сохранения «глубины» (координаты Z), а синий пока остаётся незадействованным. Отключение билинейной фильтрации также не случайно: на данном этапе она не даёт какого-либо эффекта (соседние точки в любом случае имеют одни и те же значения, с довольно резкими скачками), а в том, что я собираюсь показать дальше, она и вовсе будет вредна. Но об этом ниже.

Код отрисовки сцены я не привожу, т.к. в нём всё довольно тривиально (и, опять же, его можно посмотреть в полном исходнике), да и сам шейдер довольно примитивен. Самое любопытное в нём, пожалуй, то, что альфа-канал пока лишь проверяется на положительность, тогда как можно было бы задействовать его для эффекта освещения.
Получилось уже довольно неплохо, однако как-то плоско, плюс хотелось бы добавить собственно вращение планеты вокруг своей оси.

Что ж, к самой сфере претензий нет, однако картинка выглядит как-то… восьмибитно, что ли. И неудивительно: мы же записывали текстурные координаты в диапазоне [0..255] (максимум, доступный нам в обычных цветовых компонентах), а значит наша текстура может иметь не больше 256 точек в высоту (и 512 в ширину, учитывая вращение). Маловато, нужна как минимум 10-битная точность.
Увеличиваем разрешение
Сразу предупреждаю: описанный здесь код может криво работать на каких-либо устройствах, хотя мне удалось добиться нормальной отрисовки на всех устройствах, которые я смог подержать в руках. В любом случае, описанное здесь является обычным хаком.
Итак, у нас пока задейстованы две из трёх цветовых компоненты, т.е. 16 бит из 24. Ну так упакуем же данные так, чтобы каждая текстурная координата имела размер 12 бит, что позволит нам работать с текстурами размером до 4096 пикселей в высоту! Для этого изменим буквально три строчки в программе:
и напишем новый шейдер, учитывающий 12-битную схему адресации (именно в этом месте необходимо, чтобы билинейная фильтрация была отключена!):
Ну это же совсем другое дело! С небольшими изменениями (добавив масштабирование «щипком» и вращение пальцем) я эту программу показывал своим друзьям и колегам, и при этом спрашивал, сколько, по их мнению, в этой сцене треугольников. Результаты варьировались, да и сам вопрос вызывал подозрение в наличии подвоха (в этом случае респонденты шутили «один», что было недалеко от истины), но правильный ответ стабильно удивлял. И все, как один, спрашивали: а почему сферу можно крутить вокруг одной оси, но нельзя наклонять. Хм.
Наклон
А дело в том, что наклон в этой схеме реализовать существенно труднее. На самом деле, задача не является неразрешимой, и я с ней даже справился, но не обошлось без нюансов.
В сущности, задача сводится к тому, чтобы взять смещённую координату V, тогда как координата U не меняется: это происходит потому, что мы добавляем вращение вокруг оси X. План такой: преобразуем текстурные координаты в экранные (в диапазоне [-1..1]), применяем к ним матрицу поворота вокруг горизонтальной оси (для этого заранее запишем в новую константу uTilt синус и косинус угла наклона), а дальше воспользуемся новой координатой Y для выборки в нашей шаблонной текстуре. «Повёрнутая» координата Z нам тоже пригодится, с её помощью мы отзеркалим долготу для обратной стороны шарика). Экранную координату Z придётся посчитать явно, чтобы не делать две текстурных выборки из одной текстуры, заодно это повысит её точность.

Ура, наклон удался! Вот только странный шум на границе полушарий немного смущает. Очевидно, проблема кроется в недостаточной точности адресации в граничных точках (точки на самой окружности соответствуют слишком большому диапазону координат, один тексель расползается на интервал довольно заметной длины). В конце концов, мне удалось это победить, используя две сгенерированных текстуры вместо одной.
В итоге, можно приближать и крутить шарик почти так же, как в Google Earth. С тем отличием, что здесь — всего-навсего два треугольника.
Ну и, наконец, обещанное. Исходный код проекта доступен на GitHub.
Также можно скачать готовый .apk-файл.
Кстати, исходники для моих прошлых постов доступны там же.
Update: Кажется, мне всё-таки удалось добиться точного текстурирования на всех устройствах, это потребовало немного изменить порядок битов, а также немного подкорректировать округление цветов шаблонной текстуры. Теперь даже насильно сжатые текстуры должны работать более-менее нормально. Код на GitHub обновлён, новые .apk-файлы залиты.
Update 2: Всё-таки артефакт на границе полушарий был побеждён. Исходники и готовый .apk обновлены.
Кроме того, я добавил ещё один бонус: WebGL-версия этой демки доступна здесь.
Видео:Построение недостающих проекции сквозного отверстия в сфереСкачать

СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ
СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ – математическая дисциплина, изучающая геометрические образы (точки, линии, фигуры), находящиеся на сфере, и соотношения между ними.
По-видимому, первым обращением человечества к тому, что потом получит название сферической геометрии, была планетарная теория греческого математика Евдокса (ок. 408–355), одного из участников Академии Платона. Это была попытка объяснить движение планет вокруг Земли с помощью четырех вращающихся концентрических сфер, каждая из которых имела особую ось вращения с концами, закрепленными на охватывающей сфере, к которой, в свою очередь, были «прибиты» звезды. Таким образом объяснялись замысловатые траектории планет (в переводе с греческого «планета» – блуждающая). Именно благодаря такой модели древнегреческие ученые умели достаточно точно описывать и предсказывать движения планет. Это было необходимо, например, в мореплавании, а так же во многих других «земных» задачах, где нужно было учитывать, что Земля – не плоский блин, покоящийся на трех китах. Значительный вклад в сферическую геометрию внес Менелай из Александрии (ок. 100 н.э.). Его труд Сферика стал вершиной достижений греков в этой области. В Сферике рассматриваются сферические треугольники – предмет, которого нет у Евклида. Менелай перенес на сферу евклидову теорию плоских треугольников и в числе прочего получил условие, при котором три точки на сторонах сферического треугольника или их продолжениях лежат на одной прямой. Соответствующая теорема для плоскости в то время была уже широко известна, однако в историю геометрии она вошла именно как теорема Менелая, причем, в отличие от Птолемея (ок. 150), у которого в работах немало вычислений, трактат Менелая геометричен строго в духе евклидовой традиции.
Видео:FreeCad Сфера из треугольниковСкачать

Основные положения сферической геометрии.
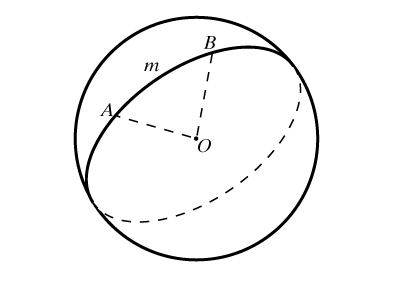
Всякая плоскость, пересекающая сферу, дает в сечении окружность. Если плоскость проходит через центр сферы, то в сечении получается так называемый большой круг. Через любые две точки на сфере, кроме диаметрально противоположных, можно провести единственный большой круг. (На глобусе примером большого круга служит экватор и все меридианы.) Через диаметрально противоположные точки проходит же бесконечное количество больших кругов. Меньшая дуга AmB (рис. 1) большого круга является кратчайшей из всех линий на сфере, соединяющих заданные точки. Такая линия называется геодезической. Геодезические линии играют на сфере ту же роль, что и прямые в планиметрии. Многие положения геометрии на плоскости справедливы и на сфере, но, в отличие от плоскости, две сферические прямые пересекаются в двух диаметрально противоположных точках. Таким образом, в сферической геометрии просто не существует понятия параллельности. Еще одно отличие – сферическая прямая замкнута, т.е. двигаясь по ней в одном и том же направлении, мы вернемся в исходную точку, точка не разбивает прямую на две части. И еще один удивительный с точки зрения планиметрии факт – треугольник на сфере может иметь все три прямых угла.
Видео:Натюрморт из геометрических предметовСкачать

Прямые, отрезки, расстояния и углы на сфере.
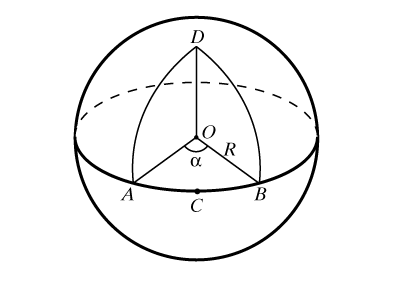
Прямыми на сфере считаются большие окружности. Если две точки принадлежат большой окружности, то длина меньшей из дуг, соединяющих эти точки, определяется как сферическое расстояние между этими точками, а сама дуга – как сферический отрезок. Диаметрально противоположные точки соединены бесконечным числом сферических отрезков – больших полуокружностей. Длина сферического отрезка определяется через радианную меру центрального угла a и радиус сферы R (рис. 2), по формуле длины дуги она равна R a. Любая точка С сферического отрезка АВ разбивает его на два, и сумма их сферических длин, как и в планиметрии, равна длине всего отрезка, т.е. РАОС + РСОВ = РАОВ. Для любой же точки D вне отрезка АВ имеет место «сферическое неравенство треугольника»: сумма сферических расстояний от D до А и от D до В больше АВ, т.е. РAOD + РDOB > РAOB, – полное соответствие между сферической и плоской геометриями. Неравенство треугольника – одно из основополагающих в сферической геометрии, из него следует, что, как и в планиметрии, сферический отрезок короче любой сферической ломаной, а значит, и любой кривой на сфере, соединяющей его концы.
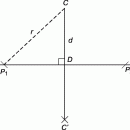
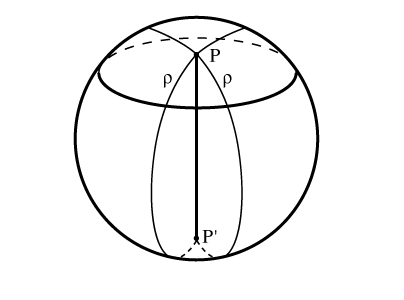
Таким же образом на сферу можно перенести и многие другие понятия планиметрии, в частности те, которые можно выразить через расстояния. Например, сферическая окружность – множество точек сферы, равноудаленных от заданной точки Р. Легко показать, что окружность лежит в плоскости, перпендикулярной диаметру сферы РР` (рис. 3), т.е. это обычная плоская окружность с центром на диаметре РР`. Но сферических центров у нее два: Р и Р`. Эти центры принято называть полюсами. Если обратиться к глобусу, то можно видеть, что идет речь именно о таких окружностях, как параллели, и сферическими центрами всех параллелей являются Северный и Южный полюса. Если диаметр r сферической окружности равен p/2, то сферическая окружность превращается в сферическую прямую. (На глобусе – экватор). В этом случае такую окружность называют полярой каждой из точек Р и P`.
Одним из важнейших понятий в геометрии является равенство фигур. Фигуры считаются равными, если одну на другую можно отобразить таким образом (поворотом и переносом), что сохранятся расстояния. Это верно и для сферической геометрии.
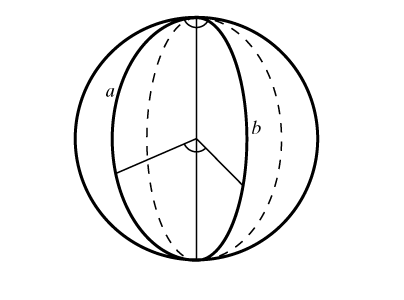
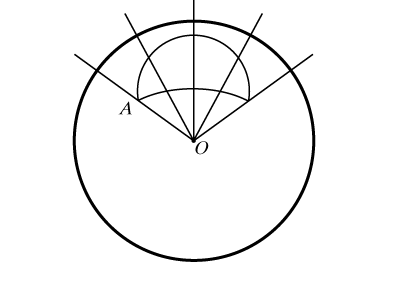
Углы на сфере определяются следующим образом. При пересечении двух сферических прямых a и b на сфере образуются четыре сферических двуугольника, подобно тому, как две пересекающиеся прямые на плоскости разбивают ее на четыре плоских угла (рис. 4). Каждому из двуугольников соответствует двугранный угол, образованный диаметральными плоскостями, содержащими a и b. А угол между сферическими прямыми равен меньшему из углов образуемых ими двуугольников.
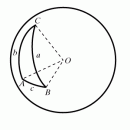
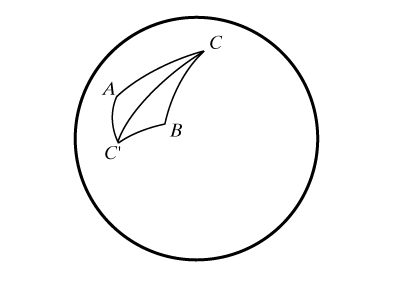
Отметим так же, что угол РABC, образованный на сфере двумя дугами большого круга, измеряют углом РA`BC` между касательными к соответствующим дугам в точке В (рис. 5) или двугранным углом, образованным диаметральными плоскостями, содержащими сферические отрезки АВ и ВС.
Точно так же, как и в стереометрии, каждой точке сферы сопоставляется луч, проведенный из центра сферы в эту точку, а любой фигуре на сфере – объединение всех пересекающих ее лучей. Так, сферической прямой соответствует содержащая ее диаметральная плоскость, сферическому отрезку – плоский угол, двуугольнику – двугранный угол, сферической окружности – коническая поверхность, ось которой проходит через полюсы окружности.
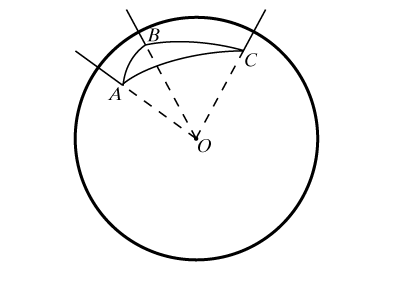
Многогранный угол с вершиной в центре сферы пересекает сферу по сферическому многоугольнику (рис. 6). Это область на сфере, ограниченная ломаной из сферических отрезков. Звенья ломаной – стороны сферического многоугольника. Их длины равны величинам соответствующих плоских углов многогранного угла, а величина угла при любой вершине А равна величине двугранного угла при ребре ОА.
Видео:Геометрия 11 класс (Урок№8 - Сфера и шар.)Скачать

Сферический треугольник.
Среди всех сферических многоугольников наибольший интерес представляет сферический треугольник. Три больших окружности, пересекаясь попарно в двух точках, образуют на сфере восемь сферических треугольников. Зная элементы (стороны и углы) одного из них, можно определить элементы все остальных, поэтому рассматривают соотношения между элементами одного из них, того, у которого все стороны меньше половины большой окружности. Стороны треугольника измеряются плоскими углами трехгранного угла ОАВС, углы треугольника – двугранными углами того же трехгранного угла (рис. 7).
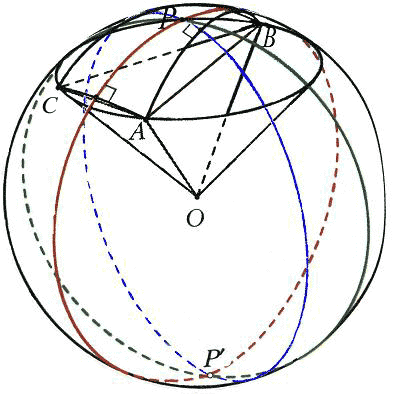
Многие свойства сферического треугольника (а они одновременно являются и свойствами трехгранных углов) почти полностью повторяют свойства обычного треугольника. Среди них – неравенство треугольника, которое на языке трехгранных углов гласит, что любой плоский угол трёхгранного угла меньше суммы двух других. Или, например, три признака равенства треугольников. Все планиметрические следствия упомянутых теорем вместе с их доказательствами остаются справедливыми на сфере. Так, множество точек, равноудаленных от концов отрезка, будет и на сфере перпендикулярной к нему прямой, проходящей через его середину, откуда следует, что серединные перпендикуляры к сторонам сферического треугольника AВС имеют общую точку, точнее, две диаметрально противоположные общие точки Р и Р`, являющиеся полюсами его единственной описанной окружности (рис. 8). В стереометрии это означает, что около любого трёхгранного угла можно описать конус. Легко перенести на сферу и теорему о том, что биссектрисы треугольника пересекаются в центре его вписанной окружности.
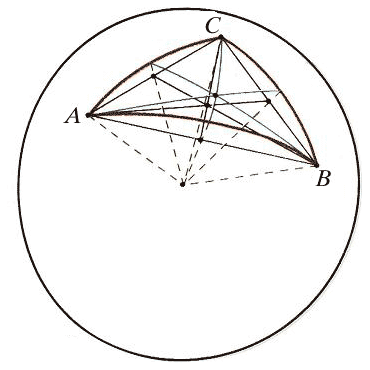
Теоремы о пересечении высот и медиан также остаются верными, но их обычные доказательства в планиметрии прямо или косвенно используют параллельность, которой, на сфере нет, и потому проще доказать их заново, на языке стереометрии. Рис. 9 иллюстрирует доказательство сферической теоремы о медианах: плоскости, содержащие медианы сферического треугольника АВС, пересекают плоский треугольник с теми же вершинами по его обычным медианам, следовательно, все они содержат радиус сферы, проходящий через точку пересечения плоских медиан. Конец радиуса и будет общей точкой трех «сферических» медиан.
Свойства сферических треугольников во многом отличаются от свойств треугольников на плоскости. Так, к известным трем случаям равенства прямолинейных треугольников добавляется еще и четвертый: два треугольника АВС и А`В`С` равны, если равны соответственно три угла РА = РА`, РВ = РВ`, РС = РС`. Таким образом, на сфере не существует подобных треугольников, более того, в сферической геометрии нет самого понятия подобия, т.к. не существует преобразований, изменяющих все расстояния в одинаковое (не равное 1) число раз. Эти особенности связаны с нарушением евклидовой аксиомы о параллельных прямых и также присущи геометрии Лобачевского. Треугольники, имеющие равные элементы и различную ориентацию, называются симметричными, таковы, например, треугольники АС`С и ВСС` (рис. 10).
Сумма углов всякого сферического треугольника всегда больше 180°. Разность РА+РВ +РС – p = d (измеряемая в радианах) – величина положительная и называется сферическим избытком данного сферического треугольника. Площадь сферического треугольника: S = R2 d где R – радиус сферы, а d – сферический избыток. Эта формула впервые была опубликована голландцем А.Жираром в 1629 и названа его именем.
Если рассматривать двуугольник с углом a, то при 226 = 2p/n (n – целое число) сферу можно разрезать ровно на п копий такого двуугольника, а площадь сферы равна 4пR 2 = 4p при R = 1, поэтому площадь двуугольника равна 4p/n = 2a. Эта формула верна и при a = 2pт/п и, следовательно, верна для всех a. Если продолжить стороны сферического треугольника АВС и выразить площадь сферы через площади образующихся при этом двуугольников с углами А, В, С и его собственную площадь, то можно прийти к вышеприведенной формуле Жирара.
Видео:№583. Стороны треугольника касаются сферы радиуса 5 см. Найдите расстояние от центра сферы до плоскоСкачать

Координаты на сфере.
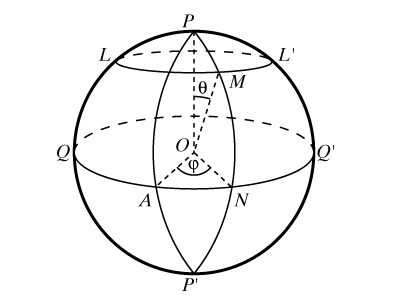
Каждая точка на сфере вполне определяется заданием двух чисел; эти числа (координаты) определяются следующим образом (рис. 11). Фиксируется некоторый большой круг QQ` (экватор), одна из двух точек пересечения диаметра сферы PP`, перпендикулярного к плоскости экватора, с поверхностью сферы, например Р (полюс), и один из больших полукругов PAP`, выходящих из полюса (первый меридиан). Большие полукруги, выходящие из P, называются меридианами, малые круги, параллельные экватору, такие, как LL`, – параллелями. В качестве одной из координат точки M на сфере принимается угол q = POM (высота точки), в качестве второй – угол j = AON между первым меридианом и меридианом, проходящим через точку M (долгота точки, отсчитываемая против часовой стрелки).
В географии (на глобусе) в качестве первого меридиана принято использовать Гринвичский меридиан, проходящий через главный зал Гринвичской обсерватории (Гринвич – городской округ Лондона), он разделяет Землю на Восточное и Западное полушария, соответственно и долгота бывает восточной либо западной и измеряется от 0 до 180° в обе стороны от Гринвича. А вместо высоты точки в географии принято использовать широту, т.е. угол NOM = 90° – q, отсчитываемый от экватора. Т.к. экватор делит Землю на Северное и Южное полушария, то и широта бывает северной либо южной и изменяется от 0 до 90°.
🔥 Видео
№584. Все стороны треугольника ABC касаются сферы радиуса 5 см. Найдите расстояние от центра сферыСкачать

🔥 ФОКУС с треугольником #shortsСкачать

Сферический избыток треугольникаСкачать

ТЕМА 2. ПОСТРОЕНИЕ КУБА, ЦИЛИНДРА, ШАРАСкачать

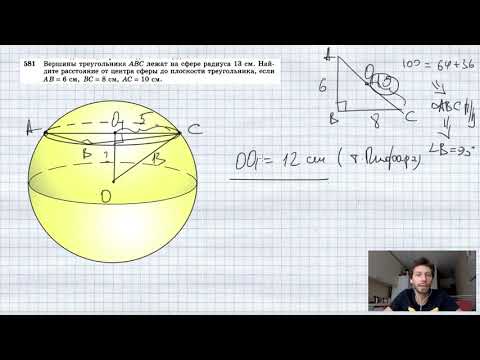
№581. Вершины треугольника ABC лежат на сфере радиуса 13 см. Найдите расстояние от центра сферы доСкачать
Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать

Сумма углов треугольника не всегда равна 180º #vertdider #veritasiumСкачать

9. Площадь сферического треугольникаСкачать

Геометрия 7 класс (Урок№9 - Треугольник.)Скачать

Как начертить КОНУС С ВЫРЕЗОМ (чертеж + аксонометрия)Скачать

Построение натуральной величины треугольника методом вращенияСкачать

Урок 3 конус, бублик, сфера, пирамида и другие геометрические фигуры в SketchUp.Скачать
Как рисовать "Свет" - А. РыжкинСкачать

Площади фигур. Сохраняй и запоминай!#shortsСкачать