Возможны два варианта построений сопряжений двух окружностей:
· Задан радиус сопряжения.
· Задана точка сопряжения на одной из окружностей.
Сопряжение может быть внешним, внутренним и смешанным.
1. Сопряжение двух окружностей дугой заданного радиуса R (Рисунок16)
При внешнем сопряжении (рисунок 16) центр сопряжения О определяется пересечением двух геометрических мест – вспомогательных окружностей радиусов R1 + R и R2 + R, проведенных соответственно из центров сопрягаемых дуг, то есть из точек О1 и О2. Точки сопряжения А и В определяются как точки пересечения заданных дуг с прямыми ОО1 и ОО2.
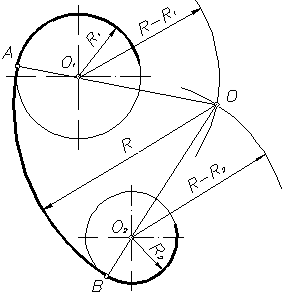
При внутреннем сопряжении (рисунок 17) центр сопряжения О определяется пересечением двух геометрических мест – вспомогательных окружностей радиусов R – R1 и R – R2, проведенных соответственно из О1 и О2 (рисунок 17).
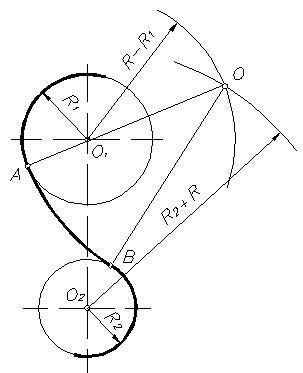
При смешанном сопряжении (рисунок 18) центр сопряжения О определяется в пересечении вспомогательных окружностей радиусов R — R1 и R + R2, проведенных соответственно из О1 и О2. Точки сопряжения А и В лежат на пересечении линий центров ОО1 и ОО2 с дугами заданных окружностей.
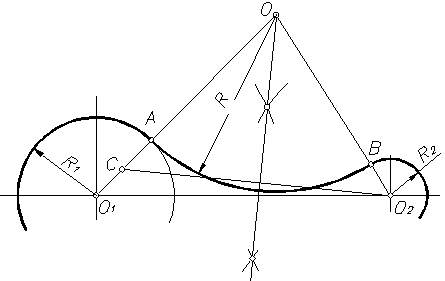
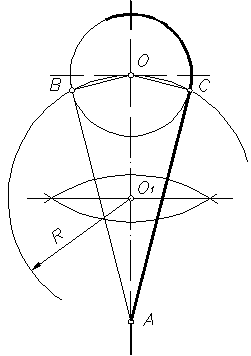
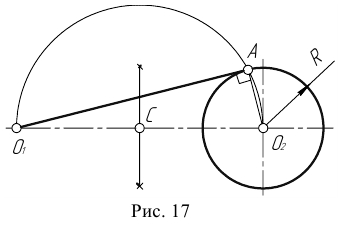
2. Сопряжение двух окружностей, если задано точка сопряжения А на одной из окружностей (рисунок 19).
Соединяют точку А с центром О1 и откладывают на этой прямой отрезок АС, равный R2. К середине отрезка СО2 восставляют перпендикуляр до пересечения с продолжением линии О1А. Точка О пересечения и является центром сопряжения. Вторая точка сопряжения В лежит на пересечении линии центров ОО2 с дугой второй окружности.
Рисунок 19
ПОСТРОЕНИЕ КАСАТЕЛЬНЫХ
Построение касательных к окружности основано на том, что касательная перпендикулярна к радиусу, проведенному в точку касания.
1. Касательная к окружности из точки А, лежащей вне окружности (рисунок 20).
Отрезок ОА, соединяющий данную точку с центром окружности, делят пополам и из полученной О1, как из центра описывают вспомогательную окружность радиусом R = О1А. Вспомогательная окружность пересекает заданную в точке С. Прямая АС является касательной к окружности, так как угол АСО прямой, как вписанный в окружность и опирающийся на ее диаметр.
2. Касательная к двум окружностям может быть внешней, если обе окружности расположены с одной стороны от нее, и внутренней, если окружности расположены с разных сторон от касательных.
2.1 Внешняя касательная к окружностям радиусов R1 и R2 (рисунок 21).
Из центра О1 большей окружности проводят вспомогательную окружность радиусом R1 – R2. Отрезок О1О2 делят пополам и проводят вспомогательную окружность радиусом R = О3О1. Точки пересечения этих окружностей соединяют с центром О1 и продолжают до пересечения с окружностью радиуса R1 в точках В и D. Эти точки являются точками касания окружности большего диаметра. Из центра О2 проводят прямые О2А и О2С, соответственно параллельные О1В и ОD, до пересечения с контуром окружности в точках А и С. Прямые АВ и СD – искомые внешние касательные к двум окружностям.
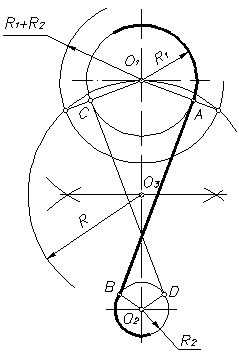
2.2 Внутренняя касательная к двум окружностям радиусов R1 и R2 (рисунок 22).
Рисунок 22
Из центра окружности О1 проводят вспомогательную окружность радиусом R1 + R2. Делят отрезок О1О2 пополам, и из полученной точки О3 проводят вторую вспомогательную окружность радиусом R = О3О1. Точки пересечения этих окружностей соединяют с центром О1 и на пересечении с окружностью радиуса R1 получают точки касания А и С. Из точки О2 проводят прямую, параллельную прямой О1А, и получают точку касания В на малой окружности. Аналогично построена точка касания D. Прямые АВ и СD – искомые внутренние касательные к двум окружностям.
- Сопряжения в инженерной графике на чертежах с примерами
- Сопряжение двух пересекающихся прямых линий
- Сопряжения прямой с окружностью
- Сопряжение двух окружностей
- Построение касательных
- Сопряжение двух параллельных прямых
- Проведение касательной к окружности
- Проведение прямой, касательной к двум окружностям
- Сопряжение дуги и прямой дугой заданного радиуса
- Сопряжение двух дуг дугой заданного радиуса
- Последовательность построения
- Построение эллипса
- 🌟 Видео
Видео:1 2 4 сопряжение окружностейСкачать

Сопряжения в инженерной графике на чертежах с примерами
Содержание:
В очертаниях технических форм часто встречаются плавные переходы от од- ной линии к другой. Плавный переход одной линии в другую, выполненный при помощи промежуточной линии, называется сопряжением. Построение сопряжений основано на следующих положениях геометрии.
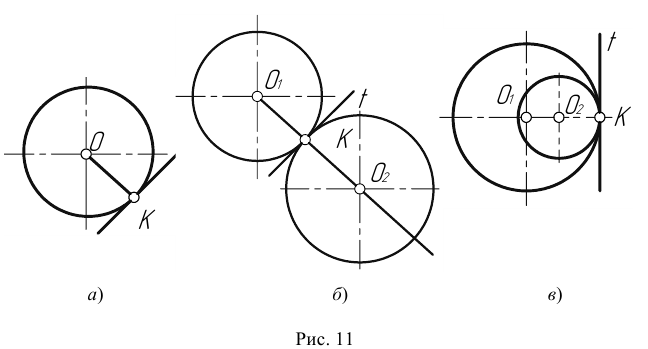
- Переход окружности в прямую будет плавным только тогда, когда заданная прямая является касательной к окружности (рис. 11а). Радиус окружности, проведенный в точку касания К, перпендикулярен к касательной прямой.
- Переход от одной окружности к другой в точке К только тогда будет плавным, когда окружности имеют в данной точке общую касательную (рис. 11б).
Точка касания К и центры окружностей
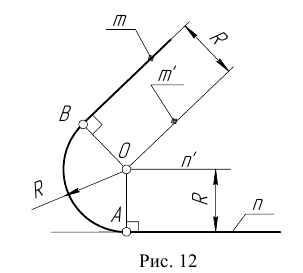
- Центром сопряжения О называется точка, равноудаленная от сопрягаемых линий (рис. 12).
- Точкой сопряжения А (В) называется точка касания двух сопрягаемых линий (рис. 12).
- Дуга сопряжения АВ – это дуга окружности, с помощью которой выполняется сопряжение (рис. 12).
- Радиус сопряжения R – это радиус дуги сопряжения (рис. 12).
Для выполнения сопряжений необходимо определить три элемента построения: 1) радиус сопряжения; 2) центр сопряжения; 3) точки сопряжения.
Видео:Внешняя касательная к двум окружностямСкачать
Сопряжение двух пересекающихся прямых линий
Пусть даны две пересекающиеся прямые m, n и радиус сопряжения R (рис. 12). Необходимо построить сопряжение данных прямых дугой окружности радиусом R.
Выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от прямой n на расстояние радиуса R сопряжения. Таким множеством является прямая
параллельная данной прямой n и отстоящая от неё на расстояние R.
- Построим множество точек центров сопряжения, удаленных от прямой m на расстояние радиуса сопряжения. Таким множеством является прямая
параллельная m и отстоящая от последней на расстояние R.
- В пересечении построенных прямых
найдем центр сопряжения О.
- Определим точку А сопряжения на прямой n. Для этого опустим из центра О перпендикуляр на прямую n . Для определения точки сопряжения В на прямой m необходимо опустить соответственно перпендикуляр из центра О на прямую m.
Проведем дугу сопряжения AB. Теперь будут определены все элементы сопряжения: радиус, центр и точки сопряжения.
Видео:Касательные к окружностиСкачать

Сопряжения прямой с окружностью
Сопряжение прямой с окружностью может быть внешним или внутренним. Рассмотрим построение внешнего сопряжения прямой с окружностью.
Пример 1. Пусть задана окружность радиусом R с центром в точке 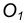
Для решения задачи выполним следующие построения:
- Построим множество точек центров сопряжения, удаленных от сопрягаемой прямой на расстояние R. Это множество задает прямая
параллельная m и отстоящая от неё на расстояние R.
- Множество точек центров сопряжения, удаленных от окружности n на рас- стояние R, есть окружность
проведенная радиусом
- Центр сопряжения О находим как точку пересечения линий
- Точку сопряжения А находим как основание перпендикуляра, проведенного из точки О на прямую m. Чтобы построить точку сопряжения В, необходимо про- вести линию центров
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
- Проведем дугу сопряжения АВ.
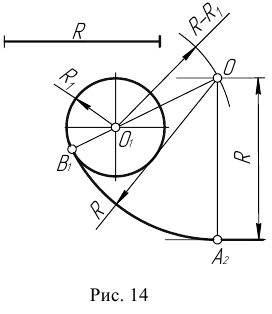
Пример 2. При построении внутреннего сопряжения (рис. 14) последовательность построений остается та же, что и в примере 1. Однако центр сопряжения определяется с помощью вспомогательной дуги окружности, проведенной из центра 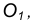
Видео:Сопряжение двух окружностей по касательной прямойСкачать

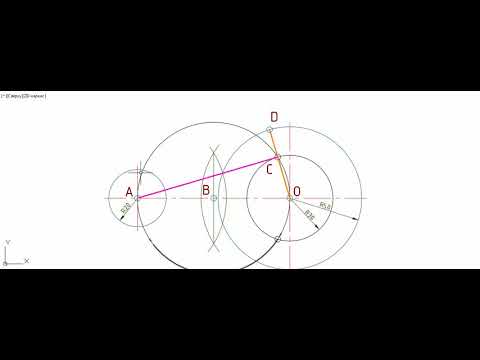
Сопряжение двух окружностей
Сопряжение двух окружностей может быть внешним, внутренним и смешанным. Пусть задан радиус сопряжения R, а центры сопряжения и точки сопряжения следует найти.
Пример 1. Построим сопряжение с внешним касанием двух данных окружностей m и n с радиусами 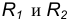
- Для нахождения центра сопряжения О проведем окружность
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
равен
- Радиусом
проведем окружность
, удаленную от данной окружности n на расстояние R.
- Найдем центр сопряжения О как точку пересечения окружностей
.
- Найдем точку сопряжения А как пересечение линии центров
с дугой m.
- Аналогично найдем точку В как пересечение линии центров
с дугой n .
- Проведем дугу сопряжения АВ.
Пример 2. Построим сопряжение с внутренним касанием двух данных окружностей m и n с радиусами 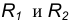
- Для нахождения центра сопряжения О проведем окружность
на расстоянии
от данной окружности m.
- Проведем окружность
на расстоянии
от данной окружности n.
- Центр сопряжения О найдем как точку пересечения окружностей
- Точку сопряжения А найдем как точку пересечения линии центров
с заданной окружностью m.
- Точку сопряжения В найдем как точку пересечения линии центров
c заданной окружностью n.
- Проведем дугу сопряжения AВ с центром в точке O.
Пример 3. На рис. 16 приведен пример построения сопряжения с внешне- внутренним касанием.
Видео:Построение внешней касательной к двум дугам окружностей. Урок11.(Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
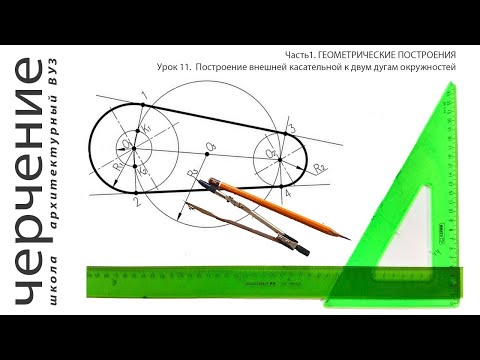
Построение касательных
Пример 1. Дана окружность с центром в точке 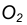
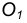
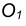
Для решения задачи выполним следующие построения.
- Соединим точку
с центром окружности
- Находим середину С отрезка
- Из точки С, как из центра, проведем вспомогательную окружность радиусом
- В точке пересечения вспомогательной окружности с заданной получим точку касания А. Соединим точку
с точкой А.
Пример 2. Построим общую касательную АВ к двум заданным окружностям радиусов 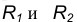
- Находим середину С отрезка
- Из точки С, как из центра, радиусом
проведем вспомогательную окружность.
- Из центра большей окружности
проведем вторую вспомогательную окружность радиусом
- Пересечение двух вспомогательных окружностей определяет точку К, через которую проходит радиус
идущий в точку касания В. 5. Для построения второй точки касания А проведем
- Соединим точки А и В отрезком прямой линии.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Нанесение размеров на чертежах
- Резьба на чертеже
- Соединения разъемные и неразъемные в инженерной графике
- Виды конструкторских документов
- Виды в инженерной графике
- Разрезы в инженерной графике
- Сечения в инженерной графике
- Выносные элементы в инженерной графике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Построение внутренней касательной к двум дугам окружностей.Урок12.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение двух параллельных прямых
Заданы две параллельные прямые и на одной из них точка сопряжения М (рис. 2.19, а). Требуется построить сопряжение.
Построение выполняют следующим образом:
- 1) находят центр сопряжения и радиус дуги (рис. 2.19, б). Для этого из точки М восставляют перпендикуляр до пересечения с прямой в точке N. Отрезок MN делят пополам (см. рис. 2.7);
- 2) из точки О – центра сопряжения радиусом ОМ = ON описывают дугу от точек сопряжения М и N (рис. 2.19, в).
Рис. 2.19. Построение сопряжения двух параллельных прямых
Видео:Построение касательной двум окружностям внешнего касанияСкачать

Проведение касательной к окружности
Даны окружность с центром О и точка А. Требуется провести из точки А касательную к окружности.
1. Точку А соединяют прямой с заданным центром О окружности.
Строят вспомогательную окружность диаметром, равным ОА (рис. 2.20, а). Чтобы найти центр О1, делят отрезок ОА пополам (см. рис. 2.7).
2. Точки M и N пересечения вспомогательной окружности с заданной – искомые точки касания. Точку А соединяют прямыми с точками М или N (рис. 2.20, б). Прямая AM будет перпендикулярна прямой ОМ, так как угол АМО опирается на диаметр.
Рис. 2.20. Проведение касательной к окружности
Видео:Построение касательной к окружности.Скачать

Проведение прямой, касательной к двум окружностям
Даны две окружности радиусов R и R1. Требуется построить прямую, касательную к ним.
Различают два случая касания: внешнее (рис. 2.21, б) и внутреннее (рис. 2.21, в).
При внешнем касании построение выполняют следующим образом:
- 1) из центра О проводят вспомогательную окружность радиусом, равным разности радиусов заданных окружностей, т.е. R – R1 (рис. 2.21, а). К этой окружности из центра О1 проводят касательную прямую Ο1Ν. Построение касательной показано на рис. 2.20;
- 2) радиус, проведенный из точки О в точку Ν, продолжают до пересечения в точке М с заданной окружностью радиуса R. Параллельно радиусу ОМ проводят радиус Ο1Ρ меньшей окружности. Прямая, соединяющая точки сопряжений М и Р, – касательная к заданным окружностям (рис. 2.21, б).
Рис. 2.21. Проведение касательной к двум окружностям
При внутреннем касании построение проводят аналогично, но вспомогательную окружность проводят радиусом, равным сумме радиусов R + R1 (рис. 2.21, в). Затем из центра О1 проводят касательную к вспомогательной окружности (см. рис. 2.20). Точку N соединяют радиусом с центром О. Параллельно радиусу ON проводят радиус O1Р меньшей окружности. Искомая касательная проходит через точки сопряжений М и Р.
Видео:Сопряжение двух пересекающихся прямых. Урок 9. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Сопряжение дуги и прямой дугой заданного радиуса
Даны дуга окружности радиуса R и прямая. Требуется соединить их дугой радиуса R1.
- 1. Находят центр сопряжения (рис. 2.22, а), который должен находиться на расстоянии R1 от дуги и от прямой. Поэтому проводят вспомогательную прямую, параллельную заданной прямой, на расстоянии, равном радиусу сопрягающей дуги R1) (рис. 2.22, а). Раствором циркуля, равным сумме заданных радиусов R + R1 описывают из центра О дугу до пересечения со вспомогательной прямой. Полученная точка О1 – центр сопряжения.
- 2. По общему правилу находят точки сопряжения (рис. 2.22, б): соединяют прямой центры сопрягаемых дуг O1 и О и опускают из центра сопряжения Ο1 перпендикуляр на заданную прямую.
- 3. Из центра сопряжения Οχ между точками сопряжения Μ и Ν проводят дугу, радиус которой R1 (рис. 2.22, б).
Рис. 2.22. Построение сопряжения окружности и прямой
Видео:Сопряжение окружностейСкачать

Сопряжение двух дуг дугой заданного радиуса
Даны две дуги, радиусы которых R1 и R2. Требуется построить сопряжение дугой, радиус которой задан.
Различают три случая касания: внешнее (рис. 2.23, а, б), внутреннее (рис. 2.23, в) и смешанное (см. рис. 2.25). Во всех случаях центры сопряжений должны быть расположены от заданных дуг на расстоянии радиуса дуги сопряжения.
Рис. 2.23. Построение сопряжения двух дуг окружностей
Построение выполняют следующим образом:
Для внешнего касания:
- 1) из центров Ο1 и О2 раствором циркуля, равным сумме радиусов заданной и сопрягающей дуг, проводят вспомогательные дуги (рис. 2.23, а); радиус дуги, проведенной из центра Ο1, равен R1 + R3; а радиус дуги, проведенной из центра O2, равен R2 + R3. На пересечении вспомогательных дуг расположен центр сопряжения – точка O3;
- 2) соединив прямыми точку Ο1 с точкой 03 и точку O2 с точкой O3, находят точки сопряжения M и N (рис. 2.23, б);
- 3) из точки 03 раствором циркуля, равным R3, между точками Μ и Ν описывают сопрягающую дугу.
Для внутреннего касания выполняют те же построения, но радиусы дуг берут равными разности радиусов заданной и сопрягающей дуг, т.е. R4 – R1 и R4 – R2. Точки сопряжения Р и К лежат на продолжении линий, соединяющих точку O4 с точками O1 и O2 (рис. 2.23, в).
Для смешанного (внешнего и внутреннего) касания (1-й случай):
- 1) раствором циркуля, равным сумме радиусов R1 и R3, из точки O2, как из центра, проводят дугу (рис. 2.24, а);
- 2) раствором циркуля, равным разности радиусов R2 и R3, из точки O2 проводят вторую дугу, пересекающуюся с первой в точке O3 (рис. 2.24, б);
- 3) из точки О1 проводят прямую линию до точки O3, из второго центра (точка O2) проводят прямую через точку O3 до пересечения с дугой в точке М (рис. 2.24, в).
Точка O3 является центром сопряжения, точки М и N – точками сопряжения;
4) поставив ножку циркуля в точку O3, радиусом R3 проводят дугу между точками сопряжения Μ и Ν (рис. 2.24, г).
Рис. 2.24. Построение сопряжения двух дуг окружностей при сочетании внешнего и внутреннего касания
Для смешанного касания (2-й случай):
- 1) две сопрягаемые дуги окружностей радиусов R1 и R2 (рис. 2.25);
- 2) расстояние между центрами О i и O2 этих двух дуг;
- 3) радиус R3 сопрягающей дуги;
- 1) определить положение центра O3 сопрягающей дуги;
- 2) найти на сопрягаемых дугах точки сопряжения;
- 3) провести дугу сопряжения
Видео:Построение общей касательной к двум окружностямСкачать

Последовательность построения
Откладывают заданные расстояния между центрами Ο1 и O2. Из центра О1 проводят вспомогательную дугу радиусом равным сумме радиусов сопрягаемой дуги радиуса R1 и сопрягающей дуги радиуса R3, а из центра O2 проводят вторую вспомогательную дугу радиусом, равным разности радиусов R3 и R2, до пересечения с первой вспомогательной дугой в точке O3, которая будет искомым центром сопрягающей дуги (рис. 2.25).
Рис. 2.25. Построение сопряжения двух дуг окружностей при смешанном касании
Точки сопряжения находят по общему правилу, соединяя прямыми центры дуг O3 и O1, O3 и O2. На пересечении этих прямых с дугами соответствующих окружностей находят точки М и N.
В технике встречаются детали, поверхности которых ограничены плоскими кривыми: эллипсом, эвольвентной окружностью, спиралью Архимеда и др. Такие кривые линии нельзя вычертить циркулем.
Их строят по точкам, которые соединяют плавными линиями с помощью лекал. Отсюда название лекальные кривые.
Эвольвента окружности приведена на рис. 2.26. Каждая точка прямой, если ее катить без скольжения по окружности, описывает эвольвенту.
Рис. 2.26. Эвольвента окружности
Рабочие поверхности зубьев большинства зубчатых колес имеют эвольвентное зацепление (рис. 2.27).
Рис. 2.27. Зубья эвольвентного профиля
Спираль Архимеда изображена на рис. 2.28. Это плоская кривая, которую описывает точка, равномерно движущаяся от центра О по вращающемуся радиусу.
Рис. 2.28. Эвольвента окружности
По спирали Архимеда нарезают канавку, в которую входят выступы кулачков самоцентрирующего трехкулачкового патрона токарного станка (рис. 2.29). При вращении конической шестерни, на обратной стороне которой нарезана спиральная канавка, кулачки сжимаются.
При выполнении этих (и других) лекальных кривых на чертеже можно для облегчения работы воспользоваться справочником.
Видео:Построение касательной к окружностиСкачать

Построение эллипса
Размеры эллипса определяются величиной его большой АВ и малой CD осей (рис. 2.30). Описывают две концентрические окружности. Диаметр большей равен длине эллипса (большой оси АВ), диаметр меньшей – ширине эллипса (малой оси CD). Делят большую окружность на равные части, например на 12. Точки деления соединяют прямыми, проходящими через центр окружностей. Из точек пересечения прямых с окружностями проводят линии, параллельные осям эллипса, как показано на рисунке. При взаимном пересечении этих линий получают точки, принадлежащие эллипсу, которые, соединив предварительно от руки тонкой плавной кривой, обводят с помощью лекала.
Рис. 2.29. Зубья эвольвентного профиля
Рис. 2.30. Построение эллипса
Практическое применение геометрических построений
Дано задание: выполнить чертеж ключа, показанного на рис. 2.31. Как это сделать?
Прежде чем начинать чертить, проводят анализ графического состава изображения, чтобы установить, какие случаи геометрических построений необходимо применить. На рис. 2.31 показаны эти построения.
Рис. 2.31. Анализ контура изображения ключа
Чтобы вычертить ключ, нужно провести взаимно перпендикулярные прямые, описать окружности, построить шестиугольники, соединив верхние и нижние их вершины прямыми, выполнить сопряжение дуг и прямых дугами заданного радиуса.
Какова последовательность этой работы?
Вначале проводят те линии, положение которых определено заданными размерами и не требует дополнительных построений (рис. 2.32, а), т.е. проводят осевые и центровые линии, описывают по заданным размерам четыре окружности и соединяют концы вертикальных диаметров меньших окружностей прямыми линиями.
Рис. 2.32. Последовательность выполнения геометрических построений при вычерчивании ключа
Дальнейшая работа по выполнению чертежа требует применения изложенных в п. 2.2 и 2.3 геометрических построений.
В данном случае нужно построить шестиугольники и выполнить сопряжение дуг с прямыми (рис. 2.32, б). Это и будет второй этап работы.
🌟 Видео
СОПРЯЖЕНИЕ ДУГ ОКРУЖНОСТЕЙ КАСАТЕЛЬНОЙ ЛИНИЕЙ [pairing 2 circles with a tangent line]Скачать
![СОПРЯЖЕНИЕ ДУГ ОКРУЖНОСТЕЙ КАСАТЕЛЬНОЙ ЛИНИЕЙ [pairing 2 circles with a tangent line]](https://i.ytimg.com/vi/PrWAEEiSuhM/0.jpg)
Сопряжение двух окружностейСкачать

Внешнее сопряжение двух дуг окружностей третьей дугой. Урок13.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Черчение. Внутреннее, внешнее и смешенное сопряжение двух окружностей.Скачать

Построение общей внешней касательной к двум окружностямСкачать

Внутренняя касательная к двум окружностямСкачать

Смешанное сопряжение двух дуг окружностей третьей дугой. Урок15.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать
Внутреннее сопряжение двух дуг окружностей третьей дугой. Урок14.(Часть1.ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

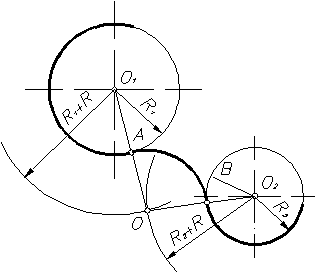

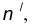 параллельная данной прямой n и отстоящая от неё на расстояние R.
параллельная данной прямой n и отстоящая от неё на расстояние R.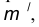 параллельная m и отстоящая от последней на расстояние R.
параллельная m и отстоящая от последней на расстояние R.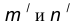 найдем центр сопряжения О.
найдем центр сопряжения О.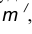 параллельная m и отстоящая от неё на расстояние R.
параллельная m и отстоящая от неё на расстояние R.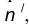 проведенная радиусом
проведенная радиусом 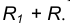
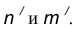
 т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.
т.е. соединить центры сопряженных дуг. В пересечении линии центров с заданной окружностью определим точку В.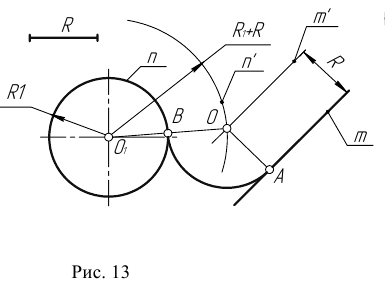
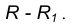
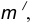 удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности
удаленную от данной окружности m на расстояние R . Так как сопряжение с внешним касанием, то радиус окружности 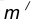 равен
равен 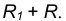
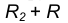 проведем окружность
проведем окружность 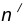 , удаленную от данной окружности n на расстояние R.
, удаленную от данной окружности n на расстояние R.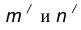 .
.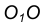 с дугой m.
с дугой m.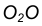 с дугой n .
с дугой n .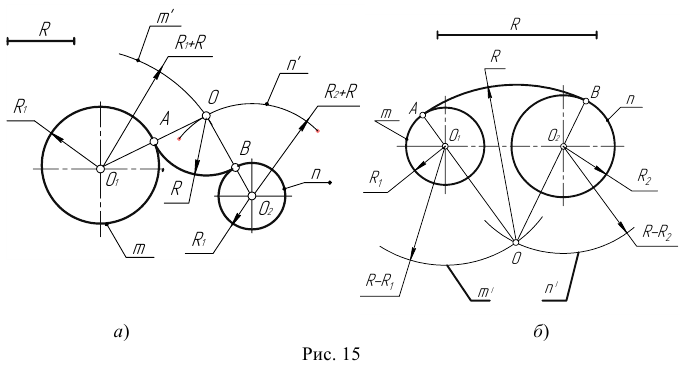
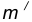 на расстоянии
на расстоянии 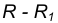 от данной окружности m.
от данной окружности m.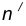 на расстоянии
на расстоянии 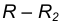 от данной окружности n.
от данной окружности n.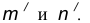
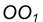 с заданной окружностью m.
с заданной окружностью m.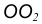 c заданной окружностью n.
c заданной окружностью n.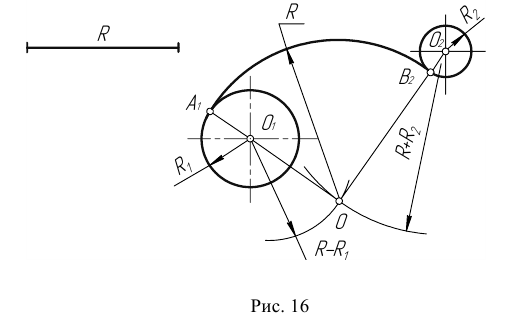
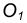 с центром окружности
с центром окружности 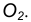
 с точкой А.
с точкой А.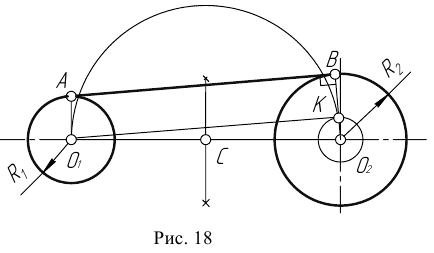
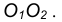
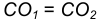 проведем вспомогательную окружность.
проведем вспомогательную окружность.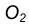 проведем вторую вспомогательную окружность радиусом
проведем вторую вспомогательную окружность радиусом 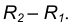
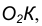 идущий в точку касания В. 5. Для построения второй точки касания А проведем
идущий в точку касания В. 5. Для построения второй точки касания А проведем