Модуль равнодействующей сил приложенных к точке движущейся по окружности

ДИНАМИКА ТОЧКИ

Определение сил по заданному движению

13.1.1Точка массой m=4 кгдвижется по горизонтальной прямой с ускорениемa=0,3t. Определить модуль силы, действующей на точку в направлении ее движения в момент времени t=3c. (3.6) Решение:Зная массу и ее ускорение, можно определить действующую на точку силу, в момент времени t=3c , ускорение будет тогда

13.1.2Ускорение движения точки массой m=27кгпо прямой задано графиком функции a=а(t). Определить модуль равнодействующей сил, приложенных к точке в момент времени t=5c. (4,05) Решение:Из графика видно что при t=5c , ускорение а=0,15м/с 2 , тогда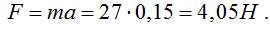

13.1.3 Деталь массой m=0,5кг скользит вниз по лотку. Под каким углом к горизонтальной плоскости должен располагаться лоток, для того чтобы деталь двигалась с ускорением а=2 м/с 2 ? Угол выразить в градусах. (11,8) Решение:Деталь движется под силой тяжести G=mg, сила под которой она движется по лотку с некоторым углом а,

13.1.4Точка массой m=14кгдвижется по горизонтальной оси Ох с ускорениемах.=lnt Определить модуль силы, действующей на точку в направлении движения в момент времени t=5c. (22,5) Решение:

13.1.5Трактор, двигаясь с ускорением а=1м/с 2 по горизонтальному участку пути, перемещает нагруженные сани массой 600кг. Определить силу тяги на крюке, если коэффициент трения скольжения саней f=0,04. (835) Решение:Необходимая сила тяги на крюке для перемещения саней с заданным ускорением 1м/с 2 :

13.1.6Тело массой m=50 кг, подвешенное на тросе, поднимается вертикально с ускорением а=0,5м/с 2 . Определить силу натяжения троса.(516) Решение:

13.1.7 Скорость движения точки m=24кг по прямой задана графиком функцииv=v(t). Определить модуль равнодействующей сил, действующих на точку. (36) Решение: из графика функции v=v(t) видно, что точка движется равноускоренно с ускорением а=1,5м/с, тогда равнодействующая сил

13.1.8 Материальная точка массой m=12кгдвижется по прямой со скоростьюv=е 0,1t . Определить модуль равнодействующей сил, действующих на точку в момент времени t=50c.(178) Решение:

13.1.9 Определить модуль равнодействующей сил, действующих на материльную точку массой m=3кг в момент времени t=6c, если она движется по оси Ох согласно уравнению х=0,04t 3 . (4,32) Решение:Ускорение точки найдем из уравнения движения (вторая производная по времени):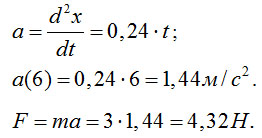

13.1.10 Материальная точка массой 1,4кг движется прямолинейно по законух=6t 2 +6t+3 . Определить модуль равнодействующей сил, приложенных к точке.(16,8) Решение:

Определение сил по заданному движению

Формула модуля равнодействующей силы

На тело могут оказывать действие не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы.

Формула равнодействующей всех сил

Пусть на тело воздействуют в один и тот же момент времени N сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Сила является векторной величиной. Следовательно, силы, действующие на тело, нужно складывать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

Формула (1) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена также как вектор ускорения тела.

Складывают векторы, используя правило треугольника (рис.1)

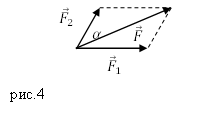
правило параллелограмма (рис.2).

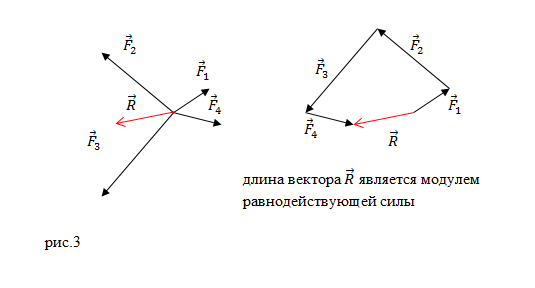
или многоугольника (рис.3):

Второй закон Ньютона и формула модуля равнодействующей

Основной закон динамики поступательного движения в механике можно считать формулой для нахождения модуля равнодействующей силы, приложенной к телу и вызывающей ускорение этого тела:

$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета тело скорость движения тела.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.

Примеры задач с решением

Задание. К материальной точке приложены силы, направленные под углом $alpha =60^circ $ друг к другу (рис.4). Чему равен модуль равнодействующей этих сил, если $F_1=40 $Н; $F_2=20 $Н?

Решение. Силы на рис. 1 сложим, используя правило параллелограмма. Длину равнодействующей силы $overline$ найдем, применяя теорему косинусов:

Вычислим модуль равнодействующей силы:

[F=sqrt<^2+^2+2cdot 40cdot 20<cos (60^circ ) >>approx 52,92 left(Нright).]

Ответ. $F=52,92$ Н

Задание. Как изменяется модуль равнодействующей силы со временем, если материальная точка массы $m$ перемещается в соответствии с законом: $s=A$, где $s$ — путь пройденный точкой; $A=const;; omega =const?$ Чему равна максимальная величина этой силы?

Решение. По второму закону Ньютона равнодействующая сил, действующих на материальную точку равна:

Следовательно, модуль силы можно найти как:

Ускорение точки будем искать, используя связь между ним и перемещением точки:

Первая производная от $s$ по времени равна:

Подставим полученный в (2.5) результат, в формулу модуля для равнодействующей силы (2.2) запишем как:

Так как косинус может быть меньше или равен единицы, то максимальное значение модуля силы, действующей на точку, составит:

Модуль равнодействующей сил приложенных к точке движущейся по окружности

На вертикальной оси укреплена горизонтальная штанга, по которой могут без трения перемещаться два груза массами m₁ = 100 г и m₂ = 300 г, связанные тонкой нерастяжимой нитью длиной l = 18 см. Определите, с какой частотой штанга вращается вокруг вертикальной оси, если натяжение нити составляет 100 Н.

Какие законы Вы используете для описания движения грузов? Обоснуйте их применение к данному случаю.

1. Рассмотрим задачу в системе отсчёта, связанной с Землей. Будем считать эту систему отсчёта инерциальной (ИСО).

2. Невесомый стрежень и грузы и образуют твёрдое тело (форма и размеры тела неизменны, расстояние между любыми двумя точками тела в силу нерастяжимости нити остаётся неизменным).

3. Изменение механической энергии твёрдого тела в ИСО равно работе внешних непотенциальных сил. На твёрдое тело «стержень и грузы» действуют внешние силы: со стороны оси, на которой вращается стержень, и потенциальные силы тяжести и . Работа силы равна нулю, так как по условию трение отсутствует. Поэтому механическая энергия твёрдого тела «стержень и грузы» сохраняется.

4. Нить, соединяющая на грузики, является невесомой, поэтому силы натяжения, действующие на каждый из грузиков, равны по модулю. Равнодействующая всех приложенных к каждому грузику сил постоянна, поэтому движение тел с постоянным по модулю ускорением.

5. Грузы считаем материальными точками, для которых применяем второй закон Ньютона.

Перейдем к решению. Запишем уравнение 2-го закона Ньютона в проекции на ось, направленную вдоль штанги к оси вращения. Для первого и второго тела соответственно

где T — сила натяжения нити, — угловая скорость вращения штанги, и — расстояния до оси вращения для первого и второго груза соответственно.

Учитывая, что расстояние между грузами находим:

Подставим найденное выражение в выражение для натяжения нити:

Отсюда частота вращения штанги:

На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m₁ = 200 г и m₂ = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.

Какие законы Вы используете для описания движения грузов? Обоснуйте их применение к данному случаю.

1. Рассмотрим задачу в системе отсчёта, связанной с Землей. Будем считать эту систему отсчёта инерциальной (ИСО).

2. Невесомый стрежень и грузы и образуют твёрдое тело (форма и размеры тела неизменны, расстояние между любыми двумя точками тела в силу нерастяжимости нити остаётся неизменным).

3. Изменение механической энергии твёрдого тела в ИСО равно работе внешних непотенциальных сил. На твёрдое тело «стержень и грузы» действуют внешние силы: со стороны оси, на которой вращается стержень, и потенциальные силы тяжести и . Работа силы равна нулю, так как в любой момент времени эта сила перпендикулярна вектору перемещения. По условию трение отсутствует, поэтому механическая энергия твёрдого тела «стержень и грузы» сохраняется.

4. Нить, соединяющая на грузики, является невесомой, поэтому силы натяжения, действующие на каждый из грузиков, равны по модулю. Равнодействующая всех приложенных к каждому грузику сил постоянна, поэтому движение тел с постоянным по модулю ускорением.

5. Грузы считаем материальными точками, для которых применяем второй закон Ньютона.

Перейдем к решению. Тела движутся по окружности под действием силы натяжения. Поскольку нить нерастяжима, то силы натяжения равны по модулю T₁ = T₂ = T. По второму закону Ньютона для каждого тела

Центростремительное ускорение тел равно В силу нерастяжимости нити сумма радиусов окружностей, по которым движется каждое тело, равно длине нити l = r₁ + r₂.

Решая совместно систему записанных уравнений, получаем: Откуда

Значит, ускорение первого тела равно

Сила натяжения нити

Подставляя численные значения величин, получаем