Геометрия подобие треугольников тест

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Тест по геометрии «Подобные треугольники» (8 класс)

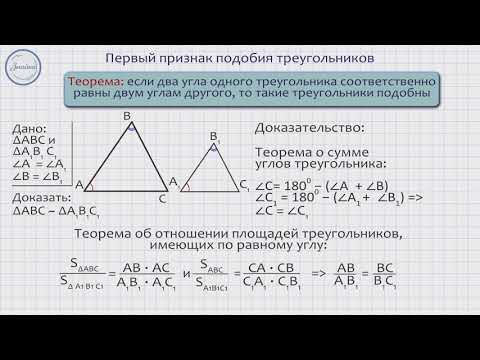
Тест можно предложить обучающимся 8 класса после прохождения темы «Отношение площадей подобных треугольников» с целью контроля за качеством усвоения понятия подобных треугольников. Тест можно предложить в качестве контроля или самоконтроля, если вывести ответы на доску. Тест и его проверка не займёт много времени на уроке.

Просмотр содержимого документа
«Тест по геометрии «Подобные треугольники» (8 класс)»

Тест по геометрии 8 класс

3. Число k, равное отношению сходственных сторон подобных треугольников, называется

а) коэффициентом подобия

б) коэффициентом сходственности

в) коэффициентом отношения

6. Отношение площадей двух подобных треугольников равно

7. Площади двух подобных треугольников равны 15 см 2 и 1215 см 2 . Найдите коэффициент подобия.

Видео:Подобие треугольников. Вся тема за 9 минут | ОГЭ по математике | Молодой РепетиторСкачать

Тесты по теме: «Подобие треугольников» (8 класс)

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

Сосковец Т.А. МБОУ СОШ №50

Тесты по теме: «Подобие треугольников» (8 класс)

Укажите условия, при которых и были бы подобны по третьему признаку.

У треугольников АВС и DEF равны углы А и D . Какого условия не достает для того, чтобы утверждать, что эти треугольники подобны по первому признаку:

В треугольниках АВС и MNK . Чему равен угол N ?

а)50 0 ; б)60 0 ; в)70 0 .

Установите по рисунку, верно ли данное утверждение:

а)ДА; б)НЕТ; в)Не возможно установить.

В треугольниках ABC и .

Соответствующие катеты двух подобных прямоугольных треугольников равны 5 дм и 10 дм. Найдите гипотенузу большего треугольника, если гипотенуза меньшего равна 7 дм.

Тест по теме: «Подобие треугольников» (8 класс)

Укажите условия, при которых и были бы подобны по первому признаку.

У треугольников АВС и DEF равны углы А и D . Какого условия не достает для того, чтобы утверждать, что эти треугольники подобны по второму признаку:

В треугольниках АВС и MNK . Чему равен угол N ?

а)35 0 ; б)75 0 ; в)80 0 .

Установите по рисунку, верно ли данное утверждение:

а)ДА; б)НЕТ; в)Не возможно установить.

В треугольниках ABC и .

Соответствующие катеты двух подобных прямоугольных треугольников равны 6 м и 18 м. Найдите гипотенузу меньшего треугольника, если гипотенуза большего равна 27 дм.

Теоретический опрос «Подобие треугольников» (8 класс)

Подобные треугольники — треугольники, у которых соответственно равны, а одного пропорциональны сторонам другого треугольника.

Коэффициент — число k, равное отношению сторон подобных треугольников.

Сходственные стороны подобных треугольников — стороны, лежащие напротив углов.

Если два одного треугольника соответственно равны . другого треугольника, то треугольники .

Если одного треугольника трём сходственным сторонам другого, то подобны.

Свойства подобных треугольников:

Отношение подобных треугольников равно квадрату подобия

Отношение равно коэффициенту подобия.

Теоретический опрос «Подобие треугольников» (8 класс)

Подобные треугольники — треугольники, у которых соответственно равны, а одного пропорциональны сторонам другого треугольника.

Коэффициент — число k, равное отношению сторон подобных треугольников.

Сходственные стороны подобных треугольников — стороны, лежащие напротив углов.

Если два одного треугольника соответственно равны . другого треугольника, то треугольники .

Если одного треугольника трём сходственным сторонам другого, то подобны.

Свойства подобных треугольников:

Отношение подобных треугольников равно квадрату подобия

Отношение равно коэффициенту подобия.

Заполните пропуски (многоточия), чтобы получилось верное высказывание.

1. Запись означает, что отрезки АВ

и CD . отрезкам MN и FT .

2. На рисунке изображен параллелограмм ABCD , поэтому подобными являются треугольники . и .

3. На рисунке АС || МК, поэтому треугольник МВК подобен треугольнику .

4. Если угол В равен . то изображенные на рисунке треугольники ABC и KNM подобны.

5. На рисунке МК || АС, АВ = 15 см, МВ = 5 см, АС = 30 см. Длина отрезка МК = . .

6. На рисунке изображена трапеция ABCD , причем АО = 27 см, ВО = 18 см, ОС = 21 см. Длина отрезка OD равна .

Площади двух подобных многоугольников равны 75 см 2 и 300 см 2 . Одна из сторон второго многоугольника равна 9 см. Поэтому сходственная сторона первого многоугольника равна .

Сходственные стороны двух подобных треугольников равны 5 дм и 10 дм. Периметр первого треугольника равен 60 дм, периметр второго треугольника равен .

9*. Известно, что ∆АВС — прямоугольный треугольник с прямым углом С, a CD — высота, проведенная из вершины С к гипотенузе АВ. Из подобия треугольников . и . следует, что AC 2 = AB * AD .

Заполните пропуски (многоточия), чтобы получилось верное высказывание.

1. Запись означает, что отрезки CD

2. На рисунке изображен параллелограмм АВС D , поэтому подобными являются треугольники . и .

3. На рисунке АВ || KD , поэтому треугольник DKC подобен треугольнику .

4. Если АС = . KN = . то изображенные на рисунке треугольники ABC и KNM подобны.

5. На рисунке МК || АС, ВК = 20 см, МК = 10 см, ВС = 30 см. Длина отрезка АС = . .

6. На рисунке изображена трапеция ABCD , причем АО = 20 см, ОС = 3 см, AD = 30 см. Длина отрезка ВС = . .

Сходственные стороны двух подобных многоугольников равны 20 см и 10 см. Площадь большего многоугольника равна 160 см 2 , площадь меньшего многоугольника равна .

Периметры подобных треугольников равны 75 см и 300 см. Одна из сторон большего треугольника равна 20 см, сходственная сторона меньшего треугольника равна .

9*. Известно, что ∆АВС — прямоугольный треугольник с прямым углом С, a CD — высота, проведенная из вершины С к гипотенузе АВ. Из подобия треугольников . и . следует, что

Установите , истинны или ложны следующие высказывания :

Два одноименных многоугольника называются подобными, если углы одного соответственно равны углам другого и сходственные стороны пропорциональны.

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

Два равносторонних треугольника всегда подобны.

Если три стороны одного треугольника соответственно пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Периметры подобных многоугольников относятся как сходственные стороны.

Стороны одного треугольника имеют длины 3 см, 4 см и 6 см. Стороны другого треугольника равны 9 см, 14 см и 18 см. Подобны ли эти треугольники?

Два равнобедренных треугольника подобны, если их углы при вершине равны, и боковые стороны пропорциональны.

Два прямоугольных треугольника подобны, если имеют по равному острому углу.

Если два угла одного треугольника равны 60° и 50°, а два угла другого треугольника равны 50° и 80°, то такие треугольники подобны.

Если каждую сторону треугольника уменьшить в 2,5 раза, то получится треугольник, подобный первоначальному.

Два ромба всегда подобны.

Два равнобедренных треугольника подобны, если их основания пропорциональны.

Установите , истинны или ложны следующие высказывания :

Два треугольника называются подобными, если их углы соответственно равны и стороны пропорциональны.

Если два треугольника имеют по равному углу, а стороны, заключающие эти углы, пропорциональны, то такие треугольники подобны.

Два квадрата всегда подобны.

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники подобны.

Стороны одного треугольника имеют длины 4 м, 5 м и 6 м. Стороны другого треугольника равны 12 м, 8 м и 10 м. Тогда эти треугольники подобны.

Площади подобных треугольников относятся как квадраты сходственных сторон.

Два параллелограмма всегда подобны.

Если два угла одного треугольника равны 45° и 75°, а два угла другого треугольника равны 60° и 45°, то такие треугольники подобны.

Два прямоугольных треугольника подобны, если катеты одного треугольника соответственно пропорциональны катетам другого.

Если каждую сторону треугольника уменьшить в 3 раза, то получится треугольник, подобный первоначальному.

Два равнобедренных треугольника подобны, если угол при основании одного треугольника равен углу при основании другого.

Два равнобедренных треугольника подобны, если их боковые стороны пропорциональны.

Признаки подобия треугольников

1. У треугольников АВС и KLM равны углы А и К. Какого условия недостаёт, чтобы утверждать, Что эти треугольники подобны по первому признаку?

1) ; 2) АВ = KL , АС = КМ; 3) ; 4) угол В равен углу L .

2. Стороны одного треугольника равны 3 см, 6 см и 7 см, а стороны подобного ему треугольника равны 15 см и 35 см. Найдите длину третьей стороны:

1) 70 см; 2) 7,5 см; 3) 30 см; 4) ответ не указан.

3. Стороны угла К пересечены прямыми АВ и СД, причём точки А и С лежат на одной стороне угла (А лежит между К и С), а В и Д – на другой стороне (В лежит между К и Д). Какой должна быть длина отрезка АС, чтобы прямые АВ и СД были параллельны, если КА = 3,6 см, КВ = 4,8 см, ВД = 2,4 см?

1) 5,4 см; 2) 1,8 см; 3) 3,2 см; 4) 2 см.

4 . ВС и АД – основания трапеции АВСД. Угол АВД равен углу ВСД. ВС = 4 см, ДС = 6 см, ВД = 8 см. Найдите АД:

1) 16 см; 2) 3 см; 3) 12 см; 4) 10 см.

5 . На сторонах АВ и ВС треугольника АВС отмечены соответственно точки К и L , так , что KL параллельно АС. Площадь треугольника К BL равна 84 см², а площадь треугольника АВС равна 336 см², АС = 30 см. Найдите К L :

1) 7,5 см; 2) 10 см; 3) 15 см; 4) ответ не указан.

Признаки подобия треугольников

1.Какие условия должны быть выполнены для того, чтобы треугольники АВС и К L М были подобны по второму признаку?

1) 2) АВ = KL , А C = KM ,; 3) ; 4)

2. Стороны одного треугольника равны 3 см, 7 см и 6 см, а две стороны подобного ему треугольника равны 10,5 см и 4,5 см. Найдите длину третьей стороны:

1) 4 см; 2) 9 см; 3) 4,5 см; 4) ответ не указан.

3. Дан треугольник АВС и внутри него отрезок КМ, параллельный АС, причём Найдите МС, если АВ = 18 см, ВК = 6 см, ВМ = 4 см:

1) 12 см; 2) 16 см; 3) 6 см; 4) 8 см.

4. В трапеции АВСД углы АВС и АСД равны. Найдите диагональ АС, если основания ВС и АД соответственно равны 24 см и 54 см:

1) 18 см; 2) 30 см; 3) 36 см; 4) 72 см.

5. Дан треугольник АВС,причём отрезок КМ параллельный АС. Площадь треугольника КВМ равна 9 см², ВМ = 6 см, МС = 2 см. Найдите площадь треугольника АВС:

1) 12 см²; 2) 16 см²; 3) 81 см²; 4) ответ не указан

«Подобие треугольников» (8 класс)

Найти подобные треугольники на чертежах:

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 952 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 675 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 311 человек из 70 регионов

Ищем педагогов в команду «Инфоурок»

Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Дистанционные курсы для педагогов

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 558 314 материалов в базе

Другие материалы

• 27.07.2019
• 1406
• 5

• 26.07.2019
• 247
• 1

• 26.07.2019
• 256
• 0

• 26.07.2019
• 441
• 10

• 25.07.2019
• 177
• 0

• 25.07.2019
• 410
• 1

• 25.07.2019
• 400
• 0

• 25.07.2019
• 866
• 12

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 27.07.2019 28312
• DOCX 774.7 кбайт
• 1252 скачивания
• Рейтинг: 3 из 5
• Оцените материал:

Настоящий материал опубликован пользователем Сосковец Татьяна Анатольевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 4 месяца
• Подписчики: 11
• Всего просмотров: 46627
• Всего материалов: 15

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Видео:Задача на подобие треугольников. А ты сможешь решить? | TutorOnline | МатематикаСкачать

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Египте нашли древние школьные «тетрадки»

Время чтения: 1 минута

Петербургская учительница уволилась после чтения на уроке Введенского и Хармса

Время чтения: 3 минуты

В Рособрнадзоре рассказали, как будет меняться ЕГЭ

Время чтения: 2 минуты

Власти Бурятии заявили о нехватке школьных учителей и воспитателей

Время чтения: 2 минуты

У 76% российских учителей оклад ниже МРОТ

Время чтения: 2 минуты

Полный перевод школ на дистанционное обучение не планируется

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Решение задач на тему "Подобные треугольники". 8 классСкачать

Тест по теме «Подобные треугольники»

тест на 2 варианта состоит из 7 вопросов с тремя вариантами ответов

Просмотр содержимого документа
«Тест по теме «Подобные треугольники»»

Тест по теме: «Подобие треугольников» (8 класс)

1). Если стороны одного треугольника пропорциональны сторонам другого треугольника, то треугольники:

2). Если треугольники подобны, то……

а) стороны равны

б) углы пропорциональны

3).У треугольников АВС и DEK равны углы А и D. Какого условия не достает для того, чтобы утверждать, что эти треугольники подобны по первому признаку:

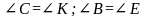
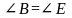
а) ; в) ;

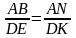
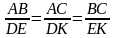
б) ; г) .

4). Углы треугольника равны 20°, 40°, А°. Угол, соответствующий углу А подобного треугольника, равен….

5). Стороны одного треугольника равны 15см, 21см, 30см. Две стороны подобного ему треугольника – 10см и 5см. Длина третьей стороны…

6).Установите, верно ли данное утверждение:

,если угол А равен углу О, АВ=10, АС=6, ОЕ=5, ОР=3.

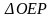
в)Не возможно установить.

7).

, АВ=4, ВС=6, АС=7, MH=8. Сторона HK равна:

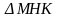
Тест по теме: «Подобие треугольников» (8 класс)

1). Если углы одного треугольника равны углам другого треугольника, то треугольники…

2). Если треугольники подобны, то…

а) стороны пропорциональны

б) стороны равны

в) углы пропорциональны

3).У треугольников АВС и DEК равны углы А и D. Какого условия не достает для того, чтобы утверждать, что эти треугольники подобны по второму признаку:

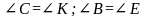
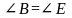
а) ; в) ;

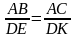
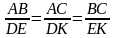
б) ; г) .

4).В подобных треугольниках АВС и MNK 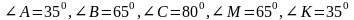. Чему равен угол N?

5).Установите, верно ли данное утверждение:

,если АВ=9,АС=12,ВС=6.ОЕ=3,ЕР=2,ОР=4.

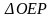
в)Не возможно установить.

_6).

, АВ=2, ВС=3, АС=1, МЕ=8. Сторона ЕК равна:

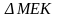
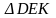
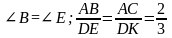
7).В треугольниках ABC и . Если ВС=12, то ЕК равна:

🎦 Видео

Подобные треугольникиСкачать

Подобные треугольники - 8 класс геометрияСкачать

8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Геометрия 8 класс (Урок№15 - Признаки подобия треугольников.)Скачать

Задача на подобие треугольников 1частьСкачать

Геометрия 8 класс. Третий признак подобия треугольниковСкачать

Подобие треугольников (ч.2) | Математика | TutorOnlineСкачать

Геометрия . Задачи на подобие треугольников. Изи.Скачать

Геометрия 8 класс (Урок№20 - Практическое приложение подобия треугольников.)Скачать

8 класс, 20 урок, Определение подобных треугольниковСкачать

Геометрия 8 класс Урок 7 Подобие Подобные треугольникиСкачать

Подобные треугольникиСкачать

Теорема ФАЛЕСА. ПОДОБИЕ ТРЕУГОЛЬНИКОВ. Контрольная № 3 Геометрия 8 класс.Скачать

Геометрия 8 класс. Первый признак подобия треугольниковСкачать

ПОДОБНЫЕ ТРЕУГОЛЬНИКИ коэффициент подобия 8 классСкачать