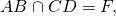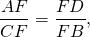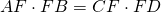Если хорды пересекаются, как этот факт можно использовать при решении задач?
Теорема
(Свойство отрезков пересекающихся хорд (пропорциональность хорд окружности))
Произведения длин отрезков пересекающихся хорд, на которые эти хорды делятся точкой пересечения, есть число постоянное.
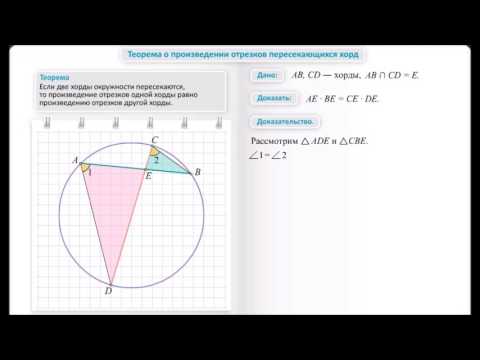
То есть, если хорды AB и CD пересекаются в точке F, то
AF ∙ FB=CF ∙ FD
Дано : окружность (O; R), AB и CD — хорды,
Доказать : AF ∙ FB=CF ∙ FD
1) Проведём отрезки BC и AD.
2) Рассмотрим треугольники AFD и CFB.
∠AFD=∠CFB (как вертикальные);
Следовательно, треугольники AFD и CFB подобны (по двум углам).
Из подобия треугольников следует пропорциональность соответствующих сторон:
то есть отрезки пересекающихся хорд пропорциональны.
По основному свойству пропорции:
Что и требовалось доказать .
При решении задач с пересекающимися хордами можно использовать не только вывод теоремы, но также полученный в ходе её доказательства факт, что пересекающиеся хорды образуют пары подобных треугольников.
Через точку M, лежащую внутри окружности, проведена хорда, которая делится точкой M на отрезки, длины которых равны 6 см и 16 см. Найти расстояние от точки M до центра окружности, если радиус окружности равен 14 см.
Дано : окружность (O; R), R=14 см, AB — хорда, M∈AB, AM=16 см, MB=6 см
Проведём через точку M диаметр CD.
По свойству отрезков пересекающихся хорд:
Пусть OM=x см (x>0). Так как радиус равен 14 см, то MD= (14-x) см, CM=(14+x) см.
Составим и решим уравнение:
Следовательно, расстояние от точки M до центра окружности равно 10 см.
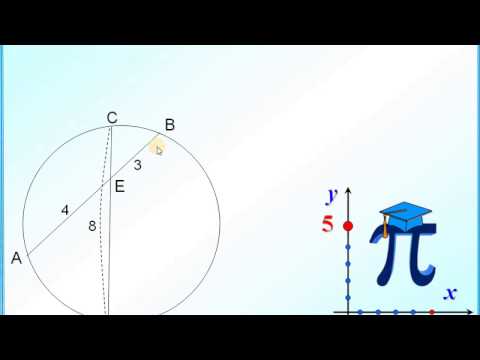
В окружности проведены хорды AB и CD , пересекающиеся в точке F. Найти длину отрезка AC, если AF=6, DF=8, BD=20.
Дано : окружность (O; R), AB и CD — хорды,
В треугольниках AFC и BFD:
∠AFC=∠BFD (как вертикальные);
∠ACF=∠DBF (как вписанные углы, опирающиеся на одну хорду AD).
Следовательно, треугольники AFC и BFD подобны (по двум углам). Поэтому
Видео:Теорема о произведении отрезков пересекающихся хорд.Скачать
Теорема о пересекающихся хордах
Теорема о пересекающихся хордах. Произведения отрезков пересекающихся хорд окружности равны.
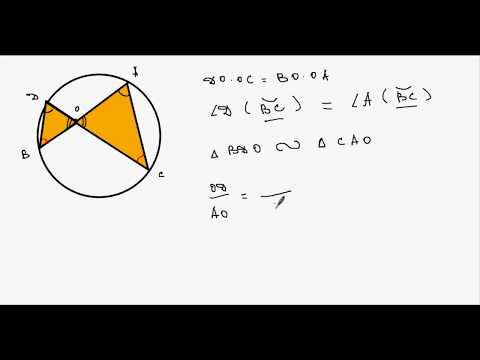
Рассмотрим треугольники AOC и DOB.
(как опирающиеся на дугу BC).
Отсюда – что и требовалось доказать.
Видео:Теорема об отрезках хорд и секущихСкачать
Это полезно
В нашей статье вы найдете всю необходимую теорию для решения задания №9 ЕГЭ по теме «Графики функций». Это задание появилось в 2022 году в вариантах ЕГЭ Профильного уровня.
Наш онлайн-курс по Физике
Все темы ЕГЭ с нуля
Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале!
Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео
Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.
Мы обязательно ответим!
Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике.
Результат будет выше, если готовиться по отработанной методике.
У нас есть онлайн-курсы как для абитуриентов, так и для преподавателей.
Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать
Теорема о произведении отрезков хорд
Теорема о произведении отрезков хорд — это утверждение элементарной геометрии, которое описывает соотношения отрезков, образованных двумя пересекающимися хордами окружности. В теореме утверждается, что произведения длин отрезков каждой из хорд равны.
Видео:11 класс, 41 урок, Две теоремы об отрезках, связанных с окружностьюСкачать
Утверждение теоремы
Для двух хорд AC и BD, пересекающихся в точке S, выполняется следующее равенство:
| A S | ⋅ | S C | = | B S | ⋅ | S D |
Обратное тоже верно, то есть если для двух отрезков AC и BD, пересекающихся в точке S, вышеприведённое равенство выполняется, то их конечные точки A, B, C и D лежат на одной окружности. Или, другими словами, если диагонали четырёхугольника ABCD пересекаются в точке S и выполняется вышеупомянутое равенство, то этот четырёхугольник является вписанным.
Видео:Математика ОГЭ Задание 24 Отрезки пересекающихся хордСкачать
Степень точки
Значения двух произведений в теореме о хордах зависит от расстояния точки пересечения S от центра окружности и называется абсолютным значением степени точки S. Более точно это можно выразить следующим образом:
где r является радиусом окружности, а d является расстоянием между центром окружности и точкой пересечения S. Это свойство следует непосредственно из применения теоремы о хордах к третьей хорде, проведённой через точку S и центр окружности M (см. рисунок).
Наряду с теоремой о секущей и касательной и теоремой о двух секущих, теорема о пересекающихся хордах представляет один из трёх основных случаев более общей теоремы о двух пересекающихся прямых и окружности — теоремы о степени точки.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Доказательство теоремы
Теорему можно доказать с помощью подобных треугольников (через теорему о вписанном угле). Рассмотрим углы треугольников ASD и BSC:
∠ A D S = ∠ B C S (углы, опирающиеся на хорду AB) ∠ D A S = ∠ C B S (углы, опирающиеся на хорду CD) ∠ A S D = ∠ B S C (вертикальные углы)
Это означает, что треугольники ASD и BSC подобны, а потому:
A S S D = B S S C ⇔ | A S | ⋅ | S C | = | B S | ⋅ | S D | <displaystyle <frac >=<frac >Leftrightarrow |AS|cdot |SC|=|BS|cdot |SD|>
🔥 Видео
теоренма об отрезках пересекающихся хордСкачать
Докажите, что произведение отрезков одной хорды равно произведению отрезков другой хордыСкачать
теорема об отрезках пересекающихся хорд и еще несколько свойств окружностиСкачать
39. Теорема об отрезках пересекающихся хордСкачать
ОГЭ 2021| Произведение отрезков двух хорд |Скачать
Произведение отрезков пересекающихся хордСкачать
Пропорциональные отрезки круга. 9 класс.Скачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Две теоремы об отрезках, связанных с окружностьюСкачать
Теорема о пероизведении отрезков пересекающихся хордСкачать
Свойство хорд, пересекающихся внутри окружностиСкачать
Задание 24 Две пересекающиеся окружностиСкачать
9 класс. Геометрия. Теорема о пропорциональности отрезков хорд и в секущих окружности. 22.05.2020.Скачать
Теорема о секущей и касательной, о секущих, о пересекающихся хордах | Теоремы об окружностях - 1Скачать
