Смещение окружности на графике

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

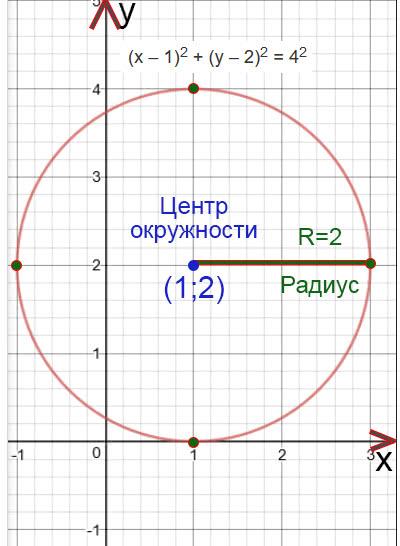
Пример №1:
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Уравнение с двумя переменными и его график. Уравнение окружности

п.1. Понятие уравнения с двумя переменными

Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.

Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.

Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).

п.2. Обобщенные правила преобразования графика уравнения

Пусть F(x; y) = 0 – исходный график некоторой функции

Симметричное отображение относительно оси OY

Симметричное отображение относительно оси OX

Центральная симметрия относительно начала координат

Параллельный перенос графика на a единиц вправо

Параллельный перенос графика на a единиц влево

Параллельный перенос графика на b единиц вниз

Параллельный перенос графика на b единиц вверх

Сжатие графика к оси OY в a раз

Сжатие графика к оси OX в b раз

F(x; by) = 0
0 Например:

Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm $$

п.4. Примеры

Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<y=frac=-frac + 2 > ) – это прямая

б) xy + 4 = 0
Выразим y из уравнения: ( mathrm<y=frac> ) – это гипербола

в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm<R=sqrt=2> )

г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<y=frac> ) – это парабола

Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<y=frac=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.

б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.

в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.

г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).

д) (mathrm<frac+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.

Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.

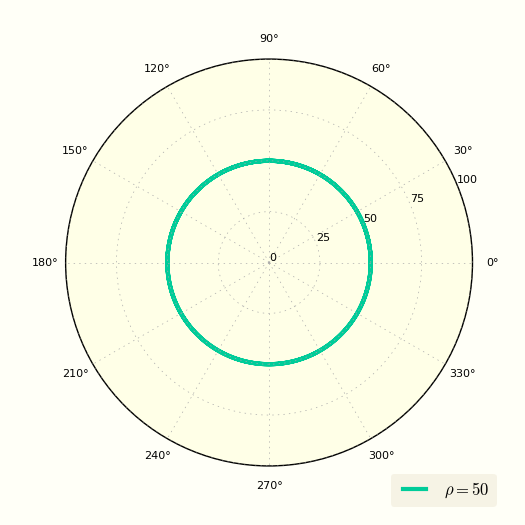
Окружность в полярных координатах

Уравнение окружности в полярных координатах выглядит очень просто

Это уравнение показывает, что ρ вообще не зависит от угла φ.

Построение окружности по простому уравнению в полярной системе координат

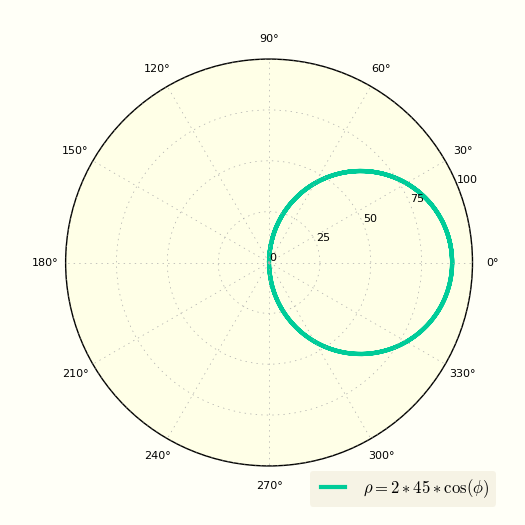
Еще одно уравнение окружности в полярных координатах

Первый пример был очень простым, теперь возьмем окружность смещенную по оси X в декартовых координатах и получим ее полярное уравнение.

Известно, что окружность в декартовой прямоугольной системе координат описывается уравнением:

Используя эти формулы и подставив их в (1) мы получим:

Уравнение окружности в полярных координатах

Изначально после подстановки имеем

И этого уравнения получается система

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.

В итоге получаем:

Построение окружности в полярной системе координат

Теперь сместим окружность по вверх, очередное уравнение окружности в полярных координатах

В данном варианте мы сместим окружность по оси Y в декартовых координатах и получим ее полярное уравнение.

При таком смещении окружность описывается уравнением:

И этого уравнения получается система

Первое уравнение системы описывает полюс окружности.

Второе описывает саму окружность в полярной системе координат.