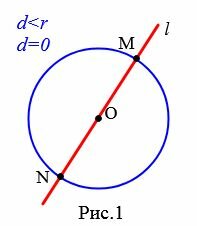
Случаи взаимного расположения прямой и окружности чертежи к ним (5 видео)

Взаимное расположение прямой и окружности

Выясним количество общих точек прямой и окружности в зависимости от их взаимного расположения. Если прямая l проходит через центр O окружности (Рис.1), то она пересекает окружность в двух точках, которые являются концами диаметра окружности.

Пусть прямая не проходит через центр окружности. Проведем перпендикуляр OH к прямой l (Рис.2, Рис.3, Рис.4). Обозначим расстояние от центра окружности до прямой l буквой d. Рассмотрим сколько общих точек будут иметь прямая и окружность в зависимости от соотношения d и r.

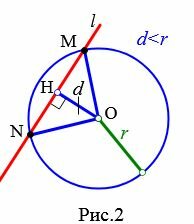Случаи взаимного расположения прямой и окружности чертежи к ним

Теорема 1. Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.

В этом случае прямая называется секущей по отношению к окружности.

Доказательство. Пусть расстояние от центра окружности до прямой меньше радиуса окружности: d Теорема 2. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.

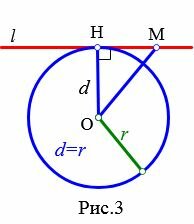Доказательство. Пусть расстояние от центра окружности до прямой равно радиусу окружности: d=r (Рис.3). В этом случае OH=r, т.е. точка H лежит на окружности и является общей точкой прямой l и окружности. Возьмем на прямой l любую точку M отличной от H. Тогда расстояние от OM больше расстояния OH=r, поскольку наклонная OM больше перпендикуляра OH к прямой l. Следовательно точка M не лежит на окружности. Получили, что точка H единственная общая точка прямой l и окружности.

Теорема 3. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

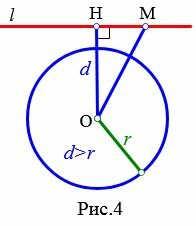Доказательство. Пусть расстояние от центра окружности до прямой больше радиуса окружности:d>r (Рис.4). Тогда ( small OH > r). Возьмем на прямой l любую точку M отличной от H. Тогда ( small OM > OH>r). Следовательно точка M не лежит на окружности. Таким образом, если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общую точку.

Видео:Окружность и прямая: варианты взаимного расположенияСкачать

Взаимное расположение прямой и окружности

Существует 3 случая взаимного расположения прямой и окружности в зависимости от соотношения между радиусом r окружности и расстоянием d прямой от центра окружности.

1. d r. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

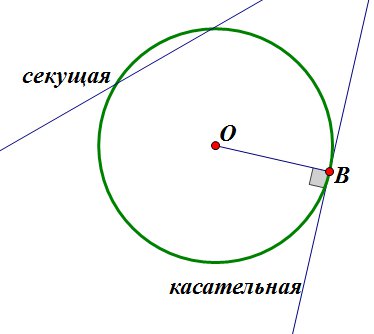
Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Прямая, имеющая с окружностью две общие точки, называется секущей.

Теоремы о касательных и секущих

Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

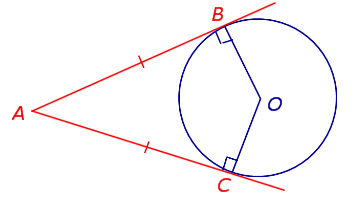
Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке: (AB=AC) .

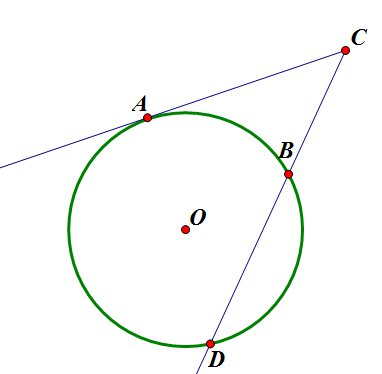
Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть: (AC^2=CDcdot BC) .

Произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть: (ACcdot BC=ECcdot DC) .

Видео:Взаимное расположение окружности и прямой. 7 класс.Скачать

Взаимное расположение прямой и окружности

Разделы: Математика

Дидактическая цель: формирование новых знаний.

Обучающие:

сформировать математические понятия: касательная к окружности, взаимное расположение прямой и окружности, добиться понимания и воспроизведения учащимися данных понятий через выполнение практической работы исследовательского характера.

Здоровьесберегающие:

создание благоприятного психологического климата на уроке;

Развивающие:

развивать у учащихся познавательный интерес, умение объяснять, обобщать полученные результаты, сравнивать, сопоставлять, делать выводы.

Воспитательные:

воспитание средствами математики культуры личности.

Формы обучения:

по содержанию – беседа, практическая работа;
по организации деятельности – индивидуальная, фронтальная.

Блоки	Этапы урока
1 блок	Организационный момент. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний.
2 блок	Постановка цели.
3 блок	Ознакомление с новым материалом. Практическая работа исследовательского характера.
4 блок	Закрепление нового материала через решение задач
5 блок	Рефлексия. Выполнение работы по готовому чертежу.
6 блок	Подведение итогов урока. Постановка домашнего задания.

Оборудование:

компьютер, экран, проектор;

раздаточный материал.

1. Математика. Учебник для 6 класса общеобразовательных учреждений; / Г.В.Дорофеев, М., Просвещение, 2009 г.

2. Маркова В.И. Особенности преподавания геометрии в условиях реализации государственного образовательного стандарта: методические рекомендации, Киров, 2010 г.

3. Атанасян Л.С. Учебник “Геометрия 7-9”.

1. Организационный момент.

Подготовка к изучению нового материала через повторение и актуализацию опорных знаний.Приветствие учеников.

Сообщает тему урока.

Выясняет, какие ассоциации возникают со словом “окружность”Записывают в тетради число и тему урока.

Отвечают на вопрос учителя.2. Постановка цели урокаОбобщает цели, сформулированные учащимися, ставит цели урокаФормулируют цели урока.3. Ознакомление с новым материалом.Организует беседу, на моделях просит показать, как могут располагаться окружность и прямая.

Организует практическую работу.

Организует работу с учебником.Отвечают на вопросы учителя.

Выполняют практическую работу, делают вывод.

Работают с учебником, находят вывод и сравнивают со своим.4. Первичное осмысление, закрепление через решение задач.Организует работу по готовым чертежам.

Работа с учебником: с. 103 № 498, №499.

Решение задачУстно решают задачи и комментируют решение.

Выполняют решение задач, комментируют.5. Рефлексия. Выполнение работы по готовому чертежуИнструктирует выполнение работы.Самостоятельно выполняют задание. Самопроверка. Подводят итоги.6. Подведение итогов. Постановка домашнего заданияУчащимся предлагается проанализировать кластер, составленный в начале урока, доработать его с учетом полученных знаний.Подводят итоги.

Учащиеся обращаются к целям, которые были поставлены, анализируют результаты: что нового узнали, чему научились на уроке

1. Организационный момент. Актуализация знаний.

Учитель сообщает тему урока. Выясняет, какие ассоциации возникают со словом “окружность”.

Чему равен диаметр окружности, если радиус равен 2,4 см?

Чему равен радиус, если диаметр равен 6,8 см?

Учащиеся ставят свои цели на урок, учитель обобщает их и ставит цели урока.

Составляется программа деятельности на уроке.

3. Ознакомление с новым материалом.

1) Работа с моделями: “Покажите на моделях, как могут располагаться прямая и окружность на плоскости”.

Сколько они имеют общих точек?

2) Выполнение практической работы исследовательского характера.

Цель. Установить свойство взаимного расположения прямой и окружности.

Оборудование: окружность, нарисованная на листе бумаги и палочка в качестве прямой, линейка.

Задание.

На рисунке (на листе бумаги) установить взаимное расположение окружности и прямой.
Измерьте радиус окружности R и расстояние от центра окружности до прямой d.
Результаты исследования запишите в таблицу.

Рисунок

Взаимное расположение

Число общих точек

Радиус окружности R

Расстояние от центра окружности до прямой d

Сравните R и d

4. Сделайте вывод о взаимном расположении прямой и окружности в зависимости от соотношения R и d.

Вывод: Если расстояние от центра окружности до прямой равно радиусу, прямая касается окружности и имеет одну общую т очку с окружностью. Если расстояние от центра окружности до прямой больше радиуса, окружность и прямая не имеют общих точек. Если расстояние от центра окружности до прямой меньше радиуса, прямая пересекает окружность и имеет с ней две общих точки.

5. Первичное осмысление, закрепление через решение задач.

1) Задания учебника: №498, № 499.

2) Определить взаимное расположении прямой и окружности, если:

1. R=16cм, d=12см
2. R=5см, d=4,2см
3. R=7,2дм, d=3,7дм
4. R=8 см, d=1,2дм
5. R=5 см, d=50мм

а) прямая и окружность не имеют общих точек;

б) прямая является касательной к окружности;

в) прямая пересекает окружность.

d-расстояние от центра окружности до прямой, R- радиус окружности.

3) Что можно сказать о взаимном расположении прямой и окружности, если диаметр окружности равен 10,3 см, а расстояние от центра окружности до прямой равно 4,15 см; 2 дм; 103 мм; 5,15 см, 1 дм 3 см.

4) Даны окружность с центром О и точка А. Где находится точка А, если радиус окружности равен 7 см, а длина отрезка ОА равна: а) 4 см; б) 10 см; в) 70 мм.

Чему научились на уроке?

Какую закономерность установили?

Выполнить на карточках следующее задание:

Проведите прямые через каждые две точки. Сколько общих точек имеет каждая из прямых с окружностью.