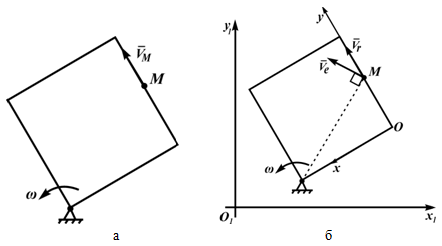
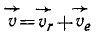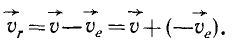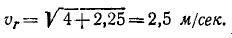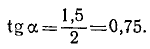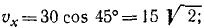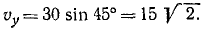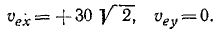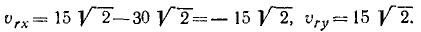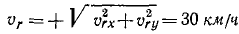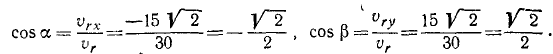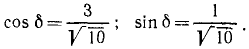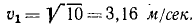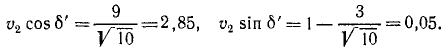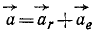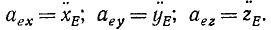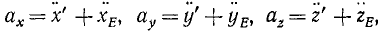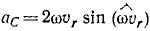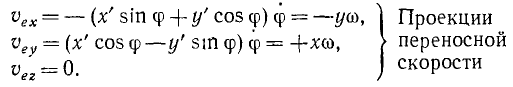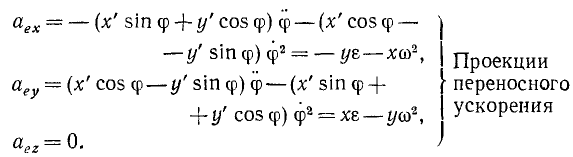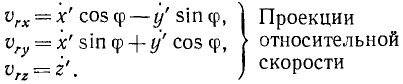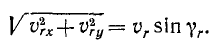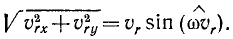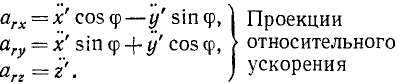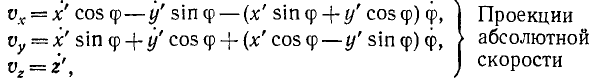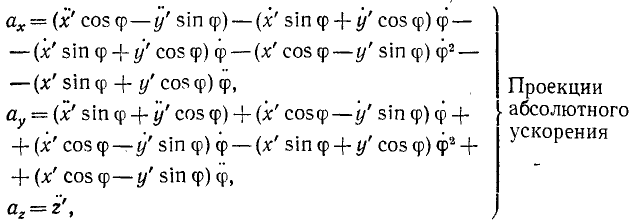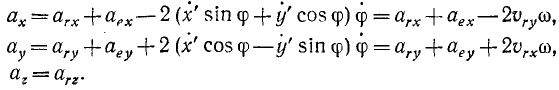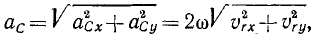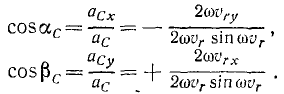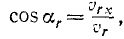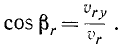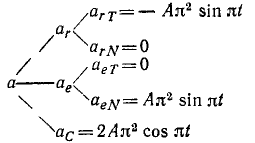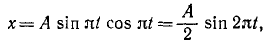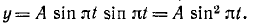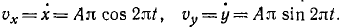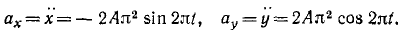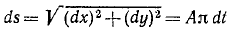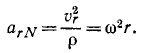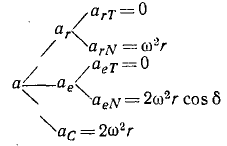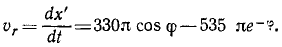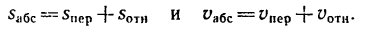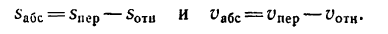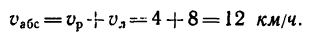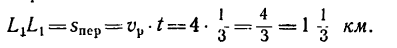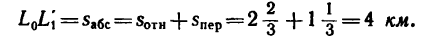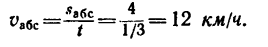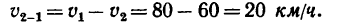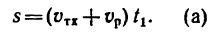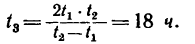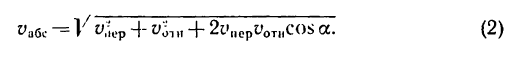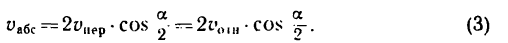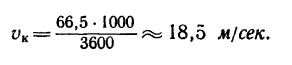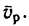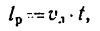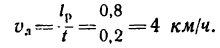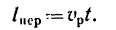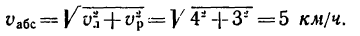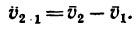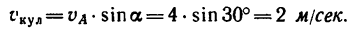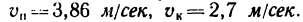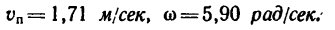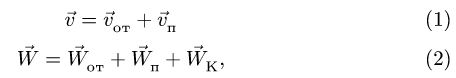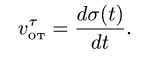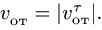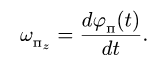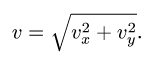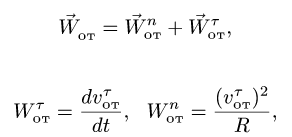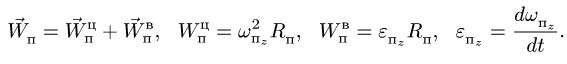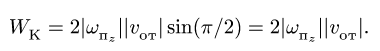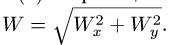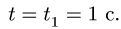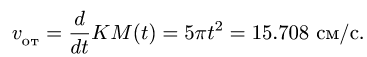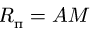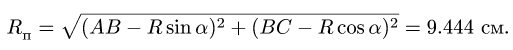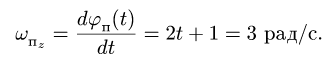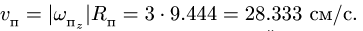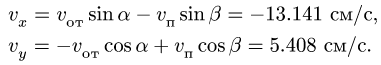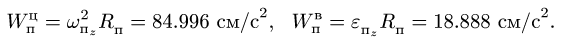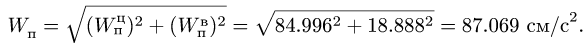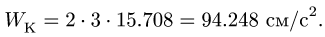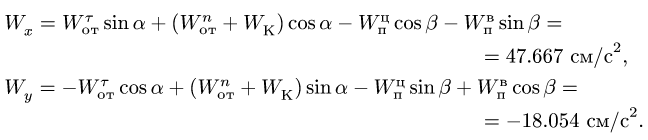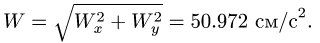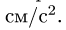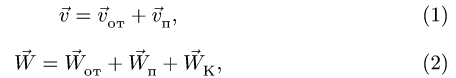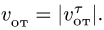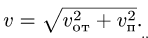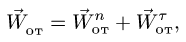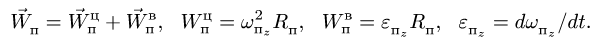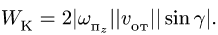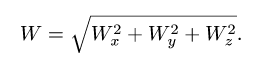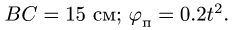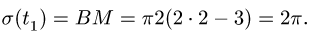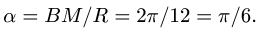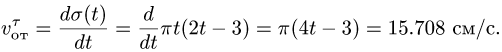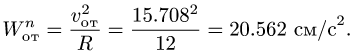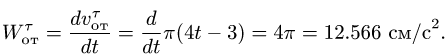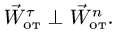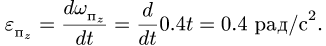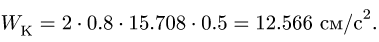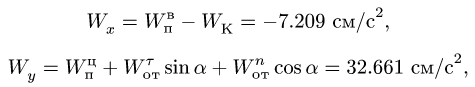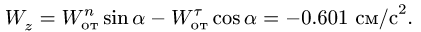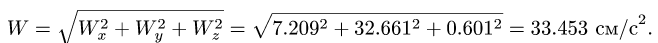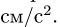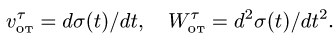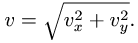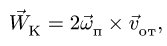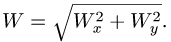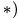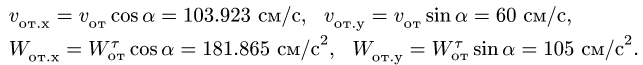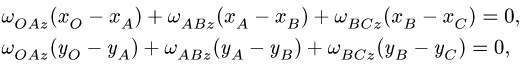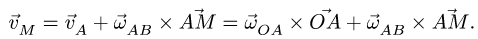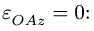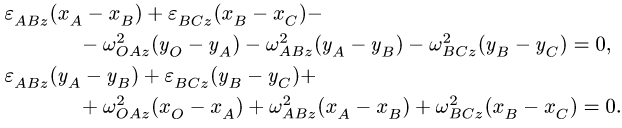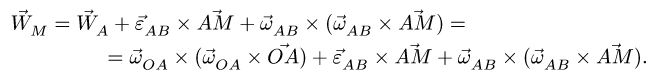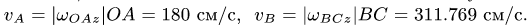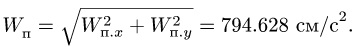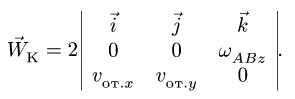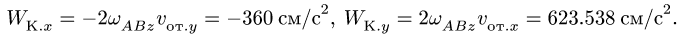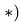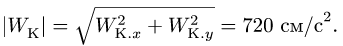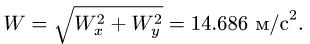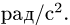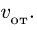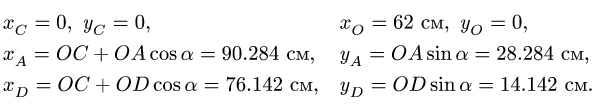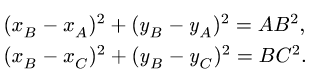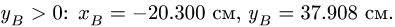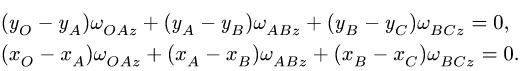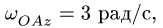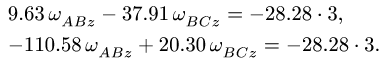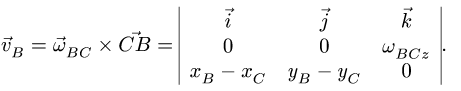Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где – кориолисово ускорение.
Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.
- Сложное (составное) движение точки
- Относительная скорость и ускорение
- Переносная скорость и ускорение
- Абсолютная скорость и ускорение
- Теорема о сложении скоростей
- Доказательство
- Теорема Кориолиса о сложении ускорений
- Доказательство
- Сложное движение точки в теоретической механике
- Сложение скоростей
- Сложение ускорений точки в общем случае переносного движения
- Ускорение Кориолиса
- Пример №1
- Пример №2
- Составное (сложное) движение. Относительное и переносное движения
- Абсолютное движение
- Относительное движение
- Переносное движение
- Составное движение
- Несколько сложнее третий пример (движение Земли)
- Теоремы параллелограмма скоростей и параллелограмма ускорений
- Относительные скорость и ускорение
- Переносные скорость и ускорение
- Параллелограмм скоростей
- Пример №3
- Пример №4
- Пример №5
- Параллелограмм ускорений
- Пример №6
- Теорема сложения ускорений точки при переносном вращательном движении (теорема Кориолиса)
- Величина ускорения Кориолиса
- При каком движении бывает ускорение Кориолиса
- Физическая причина ускорения Кориолиса
- Направление ускорения Кориолиса
- Пример №7
- Пример №8
- Задача №1
- Задача №2
- Сложное движение точки и тела
- Сложение движений точки, когда переносное и относительное движения направлены вдоль одной прямой
- Задача №3
- Задача №4
- Задача №5
- Задача №6
- Сложение движений точки, когда переносное и относительное движения направлены под углом друг к другу
- Задача №7
- Задача №8
- Задача №9
- Задача №10
- Задача №11
- Сложное движение точки в плоскости
- Задача №12
- Сложное движение точки в пространстве
- Задача №13
- Движение точки по звену механизма
- Задача №14
- Механизм с муфтой
- Задача №15
- iSopromat.ru
- 🎥 Видео
Видео:Сложное движение точки #1Скачать

Сложное (составное) движение точки
Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.
Такое движение точки называется сложным или составным.
Сложное или составное движение точки – это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.
Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).
Относительное движение точки при сложном движении – это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.
Переносное движение точки при сложном движении – это движение точки, жестко связанной телом, вызванное движением тела.
Абсолютное движение точки при сложном движении – это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.
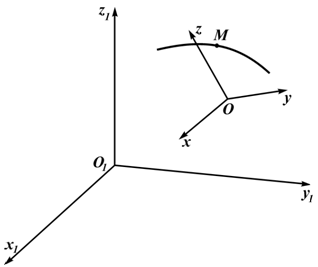
Пусть Oxyz – неподвижная система координат, On xo yo zo – подвижная система координат, жестко связанная с телом. Пусть – единичные векторы (орты), направленные вдоль осей xo , yo , zo подвижной системы координат. Тогда радиус-вектор точки M в неподвижной системе определяется по формуле:
(1) ,
где – радиус-вектор точки On – начала подвижной системы координат, связанной с телом.
Относительная скорость и ускорение
При относительном движении изменяются координаты xo , yo , zo точки относительно тела. А векторы являются постоянными, не зависящими от времени. Дифференцируя (1) по времени, считая постоянными, получаем формулы для относительной скорости и ускорения:
(2) ;
(3) .
Относительная скорость точки при сложном движении – это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела.
Относительное ускорение точки при сложном движении – это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.
Переносная скорость и ускорение
При переносном движении изменяются векторы , определяющие положение тела. Относительные координаты точки xo , yo , zo являются постоянными. Дифференцируя (1) по времени, считая xo , yo , zo постоянными, получаем формулы для переносной скорости и ускорения:
(4) ;
(5) .
Переносная скорость точки при сложном движении – это скорость точки, жестко связанной с телом, вызванная движением тела.
Переносное ускорение точки при сложном движении – это ускорение точки, жестко связанной с телом, вызванное движением тела.
Производные по времени от – это скорость и ускорение начала подвижной системы координат On : ; .
Найдем формулы для производных по времени от векторов . Для этого возьмем две произвольные точки твердого тела A и B . Их скорости связаны соотношением:
(см. страницу “Скорость и ускорение точек твердого тела”). Рассмотрим вектор , проведенный из точки A в точку B . Тогда
.
Дифференцируем по времени и применяем предыдущую формулу:
.
Итак, мы нашли формулу для производной по времени от вектора, соединяющего две точки тела:
.
Поскольку векторы жестко связаны с телом, то их производные по времени определяются по этой формуле:
(6) , , .
Подставляем в (4):
.
Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.
Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела:
,
где – угловое ускорение тела.
Абсолютная скорость и ускорение
При абсолютном движении изменяются как векторы , определяющие положение тела, так и относительные координаты точки xo , yo , zo .
Абсолютная скорость точки при сложном движении – это скорость точки в неподвижной системе координат.
Абсолютное ускорение точки при сложном движении – это ускорение точки в неподвижной системе координат.
Видео:Cложное движение точки. ТермехСкачать

Теорема о сложении скоростей
При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
.
Доказательство
Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4).
(1) ;
(7)
.
Видео:Термех. Кинематика. Сложное движение точкиСкачать

Теорема Кориолиса о сложении ускорений
При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
,
где
– кориолисово ускорение.
Доказательство
Дифференцируем (7) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (3) и (5).
(7) .
.
В последнем члене применим (6) и (2).
.
Тогда
.
Автор: Олег Одинцов . Опубликовано: 23-10-2015
Видео:Сложное движение точкиСкачать

Сложное движение точки в теоретической механике
Содержание:
Абсолютная и относительная производные от вектора:
При рассмотрении сложного движения точки в общем случае переносного движения приходится рассматривать изменение векторных величин с течением времени по отношению к системам отсчета, движущимся друг относительно друга. Одно изменение имеет векторная величина относительно подвижной системы отсчета, движущейся относительно другой, неподвижной, и другое — относительно неподвижной системы отсчета. Неподвижной системой отсчета считается система, движение которой относительно других систем отсчета не рассматривается.
Введем обозначения производных от векторных величин при рассмотрении их изменения относительно различных систем отсчета, движущихся друг относительно друга. Для любого вектора
Установим зависимость между полной и относительной производными по времени вектора 
Рис. 87
Изменение вектора 
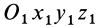
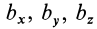
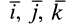
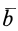
Первые три слагаемых учитывают изменение вектора 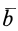
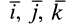
Производные по времени единичных векторов определим по формулам Пуассона
так как эти векторы не изменяются от поступательного движения со скоростью 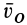
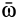
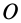
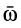
Получена формула зависимости производных векторов 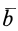
Известно, что произвольное движение системы координат как свободного твердого тела можно представить как поступательное движение вместе с полюсом, например с точкой 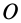
Рассмотрим частные случаи.
1. Если вектор 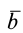
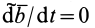
Это формула для производной от вектора постоянного модуля, доказанная ранее для радиуса-вектора при вращении вокруг неподвижной оси. Она справедлива для любого вектора при произвольном движении подвижной системы осей координат. В рассматриваемом случае 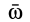
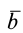
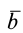
2. Если вектор 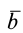
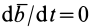
3. Если 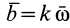
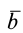
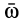
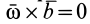
В частности, если 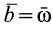
Полная и локальная производные также равны друг другу в те моменты времени, в которые вектор 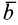
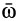
Видео:Математика это не ИсламСкачать

Сложение скоростей
Если 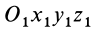
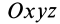
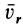
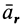
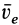
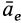
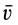
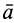
Движение подвижной системы осей координат относительно неподвижной можно охарактеризовать скоростью ее поступательного движения 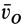
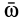
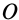
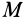
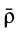
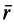
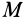
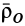
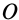
Рис. 88
Продифференцируем по времени это векторное тождество, учитывая изменения векторов относительно неподвижных осей координат, т. е. вычислим полные производные. Получим
По определению, 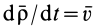
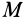
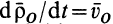
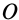
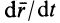
Относительная производная 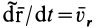
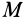
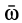
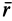
является скоростью точки свободного твердого тела, скрепленного с подвижной системой координат, с которой в данный момент совпадает точка 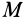
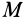
т. е. скорость абсолютного движения точки равна векторной сумме переносной и относительной скоростей.
Сложение ускорений точки в общем случае переносного движения
Абсолютное ускорение точки определим вычислением полной производной по времени от абсолютной скорости (6). Имеем
Для полных производных от векторов 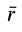
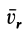
получим для абсолютного ускорения
В этой формуле первые три слагаемых составляют ускорение точки свободного твердого тела в общем случае его движения вместе с подвижной системой осей координат относительно неподвижной. Первое слагаемое 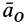
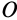
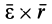
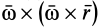
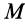
Ускорение 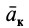
Формула (9) выражает теорему сложения ускорений точки, или кинематическую теорему Кориолиса: абсолютное ускорение точки является векторной суммой трех ускорений — переносного, относительного и Кориолиса.
Переносное ускорение рассматривалось при изучении движения свободного твердого тела. Относительное ускорение изучалось в кинематике точки. Его можно выразить в двух формах в зависимости от способа задания относительного движения. При координатном способе задания в декартовых координатах
где 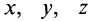
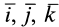
где 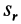
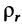
где касательное переносное ускорение
причем 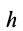
Абсолютное ускорение в этом случае
Ускорение Кориолиса
Рассмотрим ускорение Кориолиса и его свойства. Оно определяется формулой (10)
Угловую скорость вращательной части движения подвижной системы отсчета, т. е. угловую скорость переносного движения, заменили на 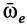
Ускорение Кориолиса является результатом взаимного влияния двух движений: переносного и относительного. Часть его 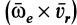
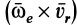
Модуль ускорения Кориолиса в соответствии с (10) определяется выражением
Для определения ускорения Кориолиса очень удобно правило Н. Е. Жуковского. Оно основано на формуле (10). Пусть имеем точку 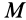
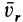
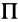
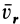
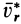
Ускорение Кориолиса выразится в форме
Рис. 89
Учитывая (10) и (12′), получаем правило Жуковского: модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направление ускорения Кориолиса, следует вектор проекции относительной скорости 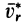
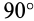
Рассмотрим случаи обращения в нуль ускорения Кориолиса. Из (12) следует, что 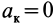
, т. е. переносное движение является поступательным;
, т. е. в те моменты времени, в которые происходит изменение направления относительного движения;
, т. е. когда скорость относительного движения
параллельна угловой скорости переносного вращения
.
Следует отметить, что при различном разложении одного и того же абсолютного движения точки на переносное и относительное получим разные ускорения Кориолиса.
Пример №1
Шар радиусом 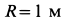
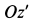
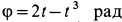
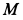
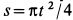
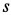
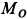
Определить абсолютные скорость и ускорение точки 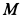
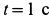
Решение. За переносное движение точки примем вращение ее вместе с шаром вокруг оси 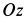
Определим положение точки 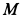
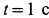
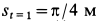
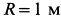
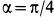
Вычислим угловые скорость и ускорение переносного движения. Получаем 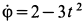
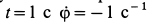
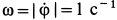
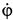
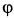
Так как 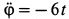
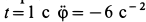
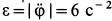
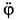
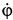
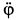
Рис. 90
Абсолютную скорость точки определяем по формуле
Скорость переносного движения при
Скорость относительного движения точки 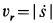
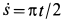
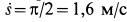
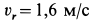
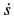
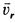
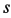
В рассматриваемом случае 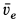
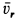
Так как переносное движение является вращением шара вокруг неподвижной оси, то абсолютное ускорение точки определяем по формуле
Переносное нормальное ускорение
Ускорение 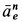
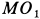
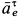
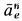
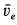
Относительное нормальное ускорение
Ускорение 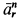
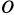
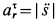
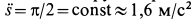
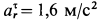
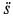
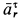
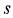
Ускорение Кориолиса определяем по правилу Жуковского. Его модуль 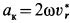
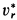
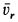
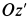
После этого находим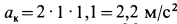
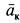
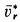
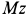
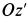
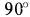
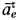
Для определения абсолютного ускорения выбираем прямоугольные оси координат 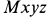
Числовое значение абсолютного значения
Пример №2
Колечко 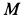
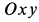
где 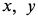
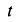
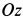
Рис.91
Определить в момент 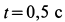
Решение. Положение колечка в момент времени 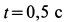
Примем движение колечка вместе с вращающимся стержнем за переносное. Тогда его движение по стержню будет относительным движением.
Вычислим проекции на оси координат абсолютных скорости и ускорения колечка для произвольного момента времени. Имеем:
Для момента времени 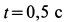
По проекциям изображаем векторы абсолютных скорости и ускорения в рассматриваемый момент времени (рис. 92). По теореме сложения скоростей для колечка,
Скорость переносного движения 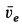
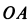
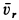
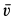
Угловая скорость вращения стержня определяется по формуле
В соответствии с направлением 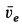
В частном случае переносного вращательного движения по теореме сложения ускорений для абсолютного ускорения имеем
Рис. 92
Вычисляем отдельные составляющие абсолютного ускорения 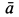
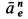
Ускорение 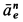
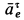
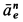
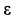
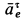
Нормальная составляющая относительного ускорения 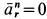
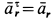
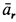
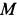
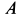
Ускорение Кориолиса 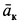
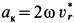
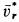
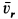
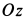
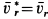
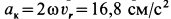
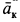
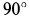
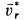
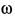
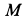
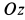
Выбираем оси координат 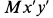
- для
- для
.
Из этих уравнений определяем неизвестные ускорения:
Ускорение 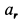
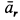
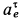
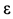
Рис. 93
Видео:Сложное движение точки. Решение задачи. Авторы: Ермишин Степан, Ходунов Алексей, Хужаев ДмитрийСкачать

Составное (сложное) движение. Относительное и переносное движения
Абсолютным движением называют движение точки или системы точек по отношению к основной системе отсчета.
Абсолютное движение
Механическое движение выражается в изменении с течением времени взаимных положений тел (или частей тела). Такое изменение можно отметить только относительно других тел. Так, река течет вдоль берегов, биллиардный шар катится по биллиардному столу, пароход пересекает экватор. Реальные или условные тела (берега, биллиардный стол, экватор), по отношению к которым мы определяем положения других движущихся тел (воды, шара, парохода) и которые мы принимаем за системы отсчета, тоже не неподвижны. Так, системы отсчета, только что приведенные нами в виде примера, находятся на поверхности нашей планеты и вместе с ней вращаются вокруг земной оси, движутся вокруг Солнца и совершают множество других движений. Но и предметы, не связанные непосредственно с Землей, тоже не неподвижны—Солнце движется относительно звезд, которые движутся относительно друг друга.
Однако для целей механики далеко не всегда нужно иметь неподвижную систему отсчета. Так, например, если мы передвигаем какой-либо груз с носа корабля на корму, то нас может интересовать движение груза по палубе независимо от движения корабля. В подобных случаях в кинематике можно условно принять за неподвижную любую систему отсчета и назвать ее основной системой отсчета. Движение же точки (или системы точек) по отношению к основной системе отсчета называют абсолютным движением.
Относительным движением называют движение точки или системы точек по отношению к подвижной системе отсчета
Относительное движение
Встречаются случаи, когда приходится изучать движение (точки или тела) по отношению к системе отсчета, которая сама передвигается относительно другой системы, принятой за основную. При рассмотрении движения точки или тела по отношению к двум системам отсчета ту из этих систем, которая движется относительно основной системы отсчета, называют подвижной системой отсчета.
Так, например, перемещение корабля в море, измеренное при помощи лага, не учитывает снос корабля морским течением. Лагом измеряют движение корабля относительно воды. Можно представить себе подвижную систему координат, плывущую вместе с водой по течению, т. е. передвигающуюся относительно другой системы отсчета, принятой за основную. Движения корабля можно рассматривать по отношению к двум системам отсчета: по отношению к подвижной системе (связанной с водой) и к основной (связанной с материками, принимаемыми за неподвижные). Движение корабля по отношению к подвижной системе координат, измеряемое лагом, будем называть относительным движением корабля. Вообще относительным движением будем называть движение (точки, тела или системы точек) по отношению к подвижной системе отсчета. Относительное движение изучают обычно в тех случаях, когда приходится учитывать не только движение данного объекта по отношению к подвижной системе отсчета, но и движение самой системы отсчета.
Переносным движением называют движение подвижной системы отсчета по отношению к основной системе отсчета
Переносное движение
Так, в данном примере, чтобы знать движение корабля относительно берегов, надо кроме движения корабля относительно воды знать также и движение самой воды, т. е. движение подвижной системы отсчета относительно основной. Движение подвижной системы отсчета по отношению к основной системе отсчета называют переносным движением.
Во многих задачах кинематики переносным бывает движение среды, в которой находится тот объект, движение которого нужно изучить. В только что рассмотренном примере течение воды действительно переносит корабль. Еще один пример: человек идет по поезду. Движение поезда является переносным движением для человека, а движение человека относительно вагонов является относительным. Поезд переносит (в буквальном смысле слова) человека. Но иногда переносное движение не является движением среды, которая увлекает с собой данный объект. Например, рассматривая движение Земли вокруг ее оси и вокруг Солнца, мы можем первое из этих движений считать относительным, а второе — переносным, хотя нет такой среды, которая вращалась бы вокруг Солнца, увлекая с собой и Землю.
Составным движением называют абсолютное движение точки или системы точек, составляемое из их относительного и переносного движений
Составное движение
В первых двух примерах движение объекта (корабля, человека) состоит из двух движений, которые мы назвали относительным и переносным. В третьем примере Земля совершает движение, которое мы искусственно разложили на относительное и переносное. Часто, чтобы упростить изучение какого-либо сложного движения, это движение искусственно раскладывают на более простые, называя одно из них относительный!, другое—переносным. Независимо от того, состоит ли движение в действительности из относительного и переносного или же мы искусственно, для упрощения расчетов, считаем его состоящим из двух движений, мы будем называть сложным или составным движением абсолютное движение точки или системы точек, состоящее (или составляемое) из относительного движения по отношению к подвижной системе отсчета и переносного движения вместе с подвижной системой отсчета.
Если в cocтавном движении мы мысленно прекратим одно из составляющих движений, то получим второе составляющее движение. При решении некоторых задач бывает удобно пользоваться таким приемом:
- чтобы определить относительное движение, мысленно остановим переносное;
- чтобы определить переносное движение, мысленно остановим относительное.
Возвращаясь к первому из только что разобранных примеров, мысленно остановим морское течение; корабль будет двигаться относительно воды, но не будет относиться течением; останется только одно движение — относительное. Остановим теперь собственный ходкорабля, но предоставим воде продолжать свое течение, и корабль поплывет по течению; останется только одно движение корабля —переносное.
Также легко выделить относительное и переносное движения во втором примере. Остановим мысленно поезд, но предоставим человеку идги по вагону, и получим относительное движение человека; остановим мысленно человека в его движении по поезду, но не будем останавливать поезд, и найдем переносное движение человека.
Движение точки, тела или системы точек часто рассматривают как составное, мысленно раскладывая его на два или несколько движений более простых
Несколько сложнее третий пример (движение Земли)
Здесь нет движения среды, переносящей Землю, подобно морскому течению, переносящему корабль. Мы лишь мысленно приняли движение Земли за составное, искусственно разложили его на переносное и относительное, чтобы упростить его, чтобы более наглядно себе его представить и легче понять. Мы можем вообразить подвижную систему координат, связанную с Землей и движущуюся относительно основной системы, связанной с Солнцем и звездами, и считать, что движение Земли состоит из переносного и относительного. Поскольку движение земного шара (движение по отношению к основной системе) мы искусственно рас: сматриваем как составное, постольку от нас самих зависит, как разложить это движение на переносное и относительное. Мы можем считать, что подвижная система отсчета движется поступательно или вращательно. В зависимости от этого, конечно, изменится и относительное движение. Земля совершает 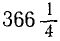
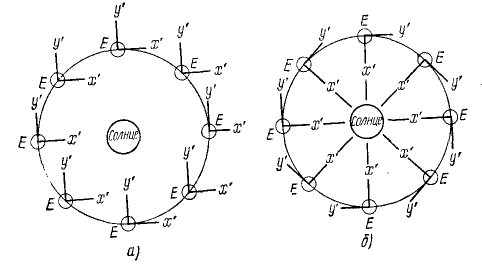
Рис. 114
Такой искусственный метод разложения движения на относительное и переносное широко применяют в различных областях механики. Л. Пуансо в предисловии ко второму изданию своей книги «Элементы статики» (1824) писал даже о невозможности представить наглядно движение тел иначе, как в виде одновременного перемещения и вращения.
Очень часто движение раскладывают не на два, а на большее число составляющих движений. Напомним, что мы уже так поступали, изучая движение точки как составное из трех прямолинейных движений, параллельных осям координат.
Теоремы параллелограмма скоростей и параллелограмма ускорений
Относительными скоростью и ускорением точки называют ее скорость и ускорение по отношению к подвижной системе отсчета
Относительные скорость и ускорение
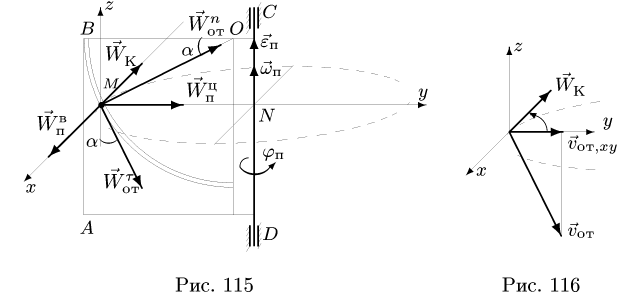
Пусть некоторая точка M (рис. 115) движется относительно системы координат.x’Ey’z’. Если бы эту систему координат мы считали неподвижной, то движение, скорость и ускорение точки по отношению к этим координатам мы называли бы абсолютными. Но пусть система координатных осей x’Ey’z’ по условиям задачи движется относительно основной системы отсчета xОyz. В таком случае скорость и ускорение точки M относительно системы координат x’Ey’z’ называют относительными.
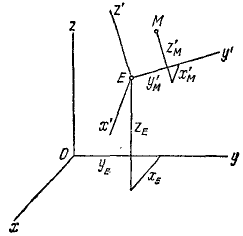
Рис. 115
- относительной скоростью точки называют скорость точки по отношению к подвижной системе отсчета1;
- относительным ускорением точки называют ускорение точки по отношению к подвижной системе отсчета.
Мы будем обозначать относительную скорость буквой υ с индексом r (от латинского слова relativus—относительный). Относительное ускорение будем обозначать буквой а с тем же индексом r.
Для обозначения проекций относительных скорости и ускорения будем ставить рядом с индексом r второй индекс. Так, υrx есть проекция относительной скорости на ось Ox; arN—относительное нормальное ускорение.
Переносными скоростью и ускорением точки называют абсолютные скорость и ускорение той точки подвижной системы отсчета, с которой в данное мгновение совпадает движущаяся точка
Переносные скорость и ускорение
Чтобы определить переносное движение точки М, прекратим мысленно ее относительное движение, закрепив ее относительно координатных осей х’Еу’z’ в том положении, которое она занимает в данное мгновение. Таким образом, мы будем считать, что точка M неизменно скреплена с осями х’Еу’z’ , но оси продолжают двигаться относительно основной системы координат xOyz вместе с точкой М. Тогда скорость и ускорение точки M относительно основных осей координат явятся скоростью и ускорением точки M в ее переносном движении.
- переносной скоростью точки M называют абсолютную скорость той точки подвижной системы отсчета, с которой в данное мгновение совпадает движущаяся точка М;
- переносным ускорением точки M называют абсолютное ускорение той точки подвижной системы отсчета, с которой в данное мгновение совпадает движущаяся точка М.
Мы будем обозначать переносную скорость точки буквой υ с индексом е (от французского слова entrainer—увлекать за собой), а переносное ускорение—буквой а с тем же индексом. Для обозначения проекций переносных скорости и ускорения на какую-либо ось будем ставить рядом с индексом е индекс, соответствующий оси.
Вектор абсолютной скорости равен сумме векторов относительной и переносной скоростей:
Параллелограмм скоростей
Ознакомившись с понятиями относительной и переносной скоростей точки, найдем зависимость между этими скоростями и абсолютной скоростью, т. е. скоростью точки по отношению к основной системе отсчета.
Пусть подвижная система координат x’Ey’z’ (рис. 116) движется поступательно. В таком случае оси Ex’, Ey’ и Ez’ будут оставаться параллельными своему начальному направлению. Для простоты выкладок пусть эти оси направлены параллельно осям основной системы координат. Тогда во все время движения будем иметь:
Ex’ ||Ox; Ey’||Oy; Ez’||Oz.
Рассмотрим сначала относительное движение точки M и для этого остановим мысленно движение подвижной системы отсчета.
Напишем уравнения движения точки M относительно подвижной системы отсчета:
x’ = x'(t). y’=y'(t), z’ = z'(t). (102)
Продифференцировав по времени и обозначая, как обычно, точкой производные по времени, найдем проекции относительной скорости на подвижные оси координат:
Так как оси подвижной системы координат параллельны соответствующим осям основной системы, то проекции относительной скорости на оси Ex’, Ey’ и Ez’ соответственно равны проекциям на параллельные им оси Ox, Oy и Oz основной системы отсчета:
Зная проекции относительной скорости, легко найдем по формулам (64) и (62) величину и направление полной относительной скорости.
Чтобы определить переносное движение, мысленно остановим движение точки относительно подвижной системы координат, но предоставим самой подвижной системе x’Ey’z’ продолжать движение.
Напишем по (77) уравнения переносного поступательного движения:
Продифференцировав равенства (77), получим проекции переносной скорости точки М, которые при поступательном движении системы равны проекциям скорости точки Е:
Величину и направление вектора полной переносной скорости точки M легко найти по формулам (64) и (62).
Для определения абсолютной скорости точки M найдем сначала ее координаты х, у и г. Применив формулу преобразования начала координатных осей при сохранении направления осей, получим
Точка M находится в составном движении, следовательно, х, у и г изменяются с течением времени, причем первые члены правых частей этих равенств изменяются согласно (102), а вторые—согласно (77). Продифференцировав по времени, получим проекции абсолютной скорости точки М:
Эти равенства показывают, что проекция абсолютной скорости на какую-либо ось равна сумме проекций относительной и переносной скоростей на ту же ось. Следовательно, вектор абсолютной скорости точки равен сумме векторов относительной скорости и переносной скорости той же точки:
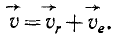
Поэтому доказанную теорему называют теоремой параллелограмма скоростей.
Равенства (103) и (103′) выражают связь между тремя скоростями (абсолютной, относительной и переносной) одной и той же точки и позволяют определить любую из этих скоростей, если известны две другие,Они доказаны в предположении, что переносное движение поступательное, но справедливы при всяком переносном движении, как это будет показано в § 31.
Из равенств (103) непосредственно получаем:
- проекция относительной скорости точки на какую-либо ось равна разности проекций абсолютной и переносной скоростей той же точки на ту же ось;
- проекция переносной скорости точки на какую-либо ось равна разности проекций абсолютной и относительной скоростей той же точки на ту же ось.
Из векторного равенства (103) получаем
Отсюда вытекает следующее правило: чтобы найти относительную скорость точки, надо сложить вектор абсолютной скорости точки с вектором, равным по модулю, но обратным по направлению вектору ее переносной скорости. Аналогично, чтобы найти переносную скорость точки, надо сложить вектор абсолютной скорости точки с вектором, равным по модулю, но обратным по направлению вектору ее относительной скорости.
Пример №3
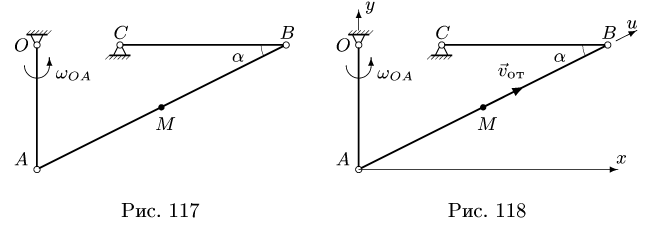
Вертикально падают дождевые капли со скоростью 2 м/сек. Пешеход идет справа налево со скоростью 1,5 м/сек. Найти скорость дождя по отношению к пешеходу (рис. 117, а).
Решение. В данной задаче за основную систему отсчета примем Землю. Подвижная система отсчета связана с пешеходом. Вертикальная скорость дождя является абсолютной скоростью (υ = 2 м/сек); переносной скоростью υe является скорость подвижной системы отсчета, т. е. скорость человека, направленная влево и равная 1,5 м/сек. Чтобы найти вектор относительной скорости, сложим вектор абсолютной скорости (рис. 117,6) с вектором, который по величине равен переносной скорости, а по направлению противоположен ей, т. е. направлен слева направо:
Вектор относительной скорости составляет с вертикалью угол а, тангенс которого равен
Пример №4
Корабль плывет на юг со скоростью 42,3 км/ч. Второй корабль идет курсом на юго-восток со скоростью 30 км/ч. Найти величину и направление скорости второго корабля, определяемую наблюдателем, находящимся на палубе первого корабля. При вычислении принять 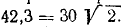
Решение. Задача аналогична предыдущей, но решать ее будем не в векторной, а в координатной форме, для чего перепишем (103) в следующем виде:
Построим основную систему координат, связанную с Землей, направив ось Ox на юг, а ось Оу— на восток, (рис. 118). Подвижную систему отсчета свяжем с первым кораблем, так как относительно первого корабля надо определить скорость второго. Проекции абсолютной скорости второго корабля на оси основной системы таковы:
Переносным движением мы называем движение подвижной системы отсчета по отношению к основной. Поэтому в данной задаче переносной скоростью является скорость первого корабля. Ее проекции следующие:
Подставляя эти значения в написанные выше уравнения, найдем проекции относительной скорости:
По проекциям находим модуль:
и направляющие косинусы относительной скорости:
Следовательно, относительная скорость второго корабля составляет углы по 45 о C положительным направлением оси Oy и с отрицательным направлением оси Ох, т. е. направлена на северо-восток.
Ответ, υr = 30 км/ч н направлена на северо-восток.
Пример №5
Ширина АВ реки (рис. 119,а) равна 900 м, и берега ее параллельны. Моторная лодка, выйдя из пункта В, держала курс перпендикулярно берегам и достигла противоположного берега через 5 мин, но не в пункте А, находящемся против В, а в пункте С, лежащем на 300 м ниже по течению. Во втором рейсе та же моторная лодка, выйдя из того же пункта В, взяла курс под углом О к BA (начальное направление на пункт D, лежащий на 300 м выше пункта А по течению) и сохраняла свое направление (угол δ), но подошла к правому берегу в пункте Е, лежащем ниже А.
Считая скорость лодки относительно воды постоянной и пренебрегая изменением течения воды у берегов, определить расстояние AE, скорость течения, скорость лодки относительно воды и скорости υ1 и υ2 лодки относительно беретов в обоих рейсах.
Решение. Возьмем начало основной системы координат в точке В, направив ось абсцисс перпендикулярно к берегу по BA, а ось ординат — вниз по течению реки (для решения задачи пользуемся формулами 103). Скорость лодки относительно этой системы является абсолютной. Подвижная система координат движется поступательно вместе с водой и скорость течения реки является переносной скоростью лодки.
Тогда, имея в виду, что АC = 300 м = DA, для первого рейса (рис. 119,6)
и для второго рейса (рис. 119, в)
В первом рейсе лодка держала курс перпендикулярно берегам и в относительном движении проплыла 900 я за 5 мин = 300 сек. Следовательно, υr=3 м/сек.
За то же время ее снесло течением на 300 м, а потому υe=l м/сек.
Подставляя эти значения в уравнения, составленные для первого рейса, и деля второе из этих уравнений на первое, найдем
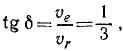
Из тех же уравнений найдем скорость лодки относительно берегов (т. е. абсолютную скорость) в первом рейсе:
Величина относительной скорости лодки, определенная по ‘данным первого рейса, не изменится и во втором, так как по условию задачи скорость лодки относительно воды постоянна. Также не изменится и переносная скорость лодки — скорость течения реки. Подставляя найденные значения в уравнения, составленные для второго рейса, получим
Из этих уравнении найдем: υ2 = 2,85 м/сек и sin δ’ = 0,018.
Умножая АB = 900 м на tg δ’, найдем AE.
Если переносное движение поступательное, то вектор абсолютного ускорения точки равен сумме векторов ее относительного и переносного ускорений
Параллелограмм ускорений
В отличие от теоремы параллелограмма скоростей, применимой при всяком переносном движении, аналогичная теорема параллелограмма ускорений справедлива только в том случае, если переносное движение поступательное.
Пусть точка совершает составное движение, причем подвижная система отсчета x’Ey’z’ движется поступательно по отношению к основной системе хОуz. Пусть соответствующие оси обеих координатных систем параллельны друг другу, это упростит доказательство.
Проекции относительной скорости точки нами уже определены. Продифференцировав эти равенства по времени, найдем проекции относительного ускорения точки:
Величину и направление полного относительного ускорения можно определить по формулам (66) и (67).
Продифференцировав по времени равенства (78), найдем проекции ускорения точки в переносном поступательном движении:
Величину и направление полного переносного ускорения можно определить по формулам (66) и (67), применимым для всякого ускорения точки, независимо от того, является это ускорение абсолютным, относительным или переносным.
Чтобы определить проекции абсолютного ускорения точки (в рассматриваемом случае переносного поступательного движения), надо продифференцировать по времени равенства (103). Получим
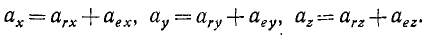
Из этих равенств видно, что если переносное движение поступательное, то проекция абсолютного ускорения точки на ось состоит из суммы проекций на ту же ось относительного и переносного ускорений точки. Следовательно, вектор абсолютного ускорения точки в этом случае равен геометрической сумме двух векторов—относительного и переносного ускорений:
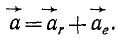
В этом заключается теорема параллелограмма ускорений.
Равенства (104) и (104′) выражают связь между абсолютным, относительным и переносным ускорениями точки в случае, если переносное движение поступательное, и позволяют определить какое-либо одно из этих ускорений по двум другим.
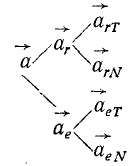
Если относительное и переносное движения заданы в естественной форме, то для определения ускорений приходится сначала определять их нормальную и касательную составляющие. Так, для определения относительного ускорения надо определить относительное касательное и относительное нормальное ускорения, а уж потом по формулам (75) и (76)—полное относительное ускорение. Аналогично для определения переносного ускорения определяют переносные касательное и нормальное ускорения, а затем полное переносное ускорение. Для получения полного абсолютного ускорения нужно взять геометрическую сумму полного относительного и полного переносного ускорений, которые составляют между собой, вообще говоря, угол, отличный от прямого.
Приводим схему разложения полного абсолютного ускорения точки для случая переносного поступательного движения. При решении задач на параллелограмм ускорений бывает полезно написать эту схему и заполнять ее справа налево:
Часто определяют абсолютное ускорение по его проекциям ах, ay, az на оси основной системы координат и, получив проекции результирующего вектора 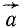
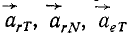
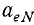
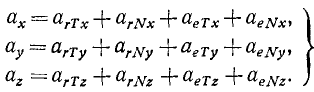
Эти равенства являются лишь некоторым видоизменением равенств (104).
Если переносное движение не поступательное, то абсолютное ускорение точки состоит из суммы трех векторов: относительного ускорения, переносного ускорения и ускорения Кориолиса. Доказательство теоремы Кориолиса дано в § 31.
Пример №6
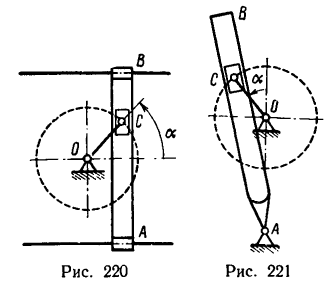
Кривошипио-кулнсный механизм приводного молота (рис. 120, а) состоит из прямолинейной поступательно движущейся кулисы АВ, в прорези которой скользит звено C (камень), соединенный шарнирно с кривошипом ОС длины e, вращающимся с постоянной угловой скоростью ω. Найти скорость и ускорение кулисы как функции угла поворота кривошипа.
Решение. Будем рассматривать движение камня C как составное, состоящее из относительного движения по прорези кулисы и переносного движения вместе с кулисой. Для решения воспользуемся формулами (103) и (104). Примем неподвижный шарнир О за начало основной системы координат, направив ось Ox вправо и ось Oy вверх (рис. 120,6). Подвижную систему координат неизменно соединим с кулисой, взяв начало в точке E и направив ось Ex’ по прорези вправо, a Ey’- вверх. Движение подвижной системы координат, как и движение кулисы, поступательное. Ось Ex’ передвигается к неподвижной оси Ох, а ось Ey’ скользит по оси Оу.
Абсолютное движение камня есть круговое поступательное движение по отношению к основной системе координат. Для определения абсолютных скорости и ускорения обратим внимание на то, что точка C (шарнир) принадлежит не только камню, но и кривошипу, а потому абсолютная скорость точки C равна ωr. (см. рис. 120, б), а ее проекции:
Абсолютное ускорение точки C равно ω 2 r, а его проекции (рис. 120, в):
ах = — ω 2 r sin ωt и ay = ω 2 r cos ωt.
Эти равенства можно было бы получить, продифференцировав предыдущие.
Относительное движение камня — это возвратно-поступательное движение по прорези вправо и влево. Такое движение камня мы видели бы, если бы сами двигались вместе с кулисой, не замечая ее движения. Камень движется по горизонтальной оси Ex’, а потому
Проекции относительного ускорения:
Переносное движение камня (движение подвижной системы отсчета относительно основной) —возвратно-поступательное движение кулисы вверх и вниз. Поэтому проекции переносных скорости и ускорения на вертикальную ось Oy равны модулям скорости и ускорения со знаком «-(-» или «—», а на горизонтальную ось Ох—равны нулю. Имеем
Из трех движений камня нас интересует переносное движение (движение кулисы). Определив проекции переносной скорости
и подставив найденные значения, получим переносную скорость из уравнений
Таким образом, переносная скорость камня (скорость кулисы) определена.
Для определения переносного ускорения мы могли бы продифференцировать по времени выражение, полученное для переносной скорости (так как переносное движение прямолинейно-поступательное). Но мы применим более общий метод — определим из (104) проекции переносного ускорения:
подставим в эти уравнения найденные нами значения проекций переносного и абсолютного ускорений камня:
0 = — ω 2 r sin ωt-ar, ae = ω 2 r cos ωt.
Таким образом, переносное ускорение ае камня равно ω 2 r cos ωt. Оно же является ускорением кулисы.
Ответ. υ = ωr sιnωt; a = ω 2 r cos ωt.
Теорема сложения ускорений точки при переносном вращательном движении (теорема Кориолиса)
При составном движении точки в случае непоступательиого переносного движения возникает добавочное ускорение, называемое ускорением Кориолиса:
Величина ускорения Кориолиса
Теорема параллелограмма ускорений пригодна только в частном случае, если подвижная система отсчета движется поступательно. Если же переносное движение не поступательное, то у абсолютного ускорения появляется еще одна составляющая, называемая ускорением Кориолиса, или поворотным ускорением. Выведем формулы, позволяющие определить абсолютное ускорение при всяком составном движении точки.
Пусть точка M (рис. 121) движется относительно подвижной системы x’0y’z’ и это движение определяется какими-либо уравнениями
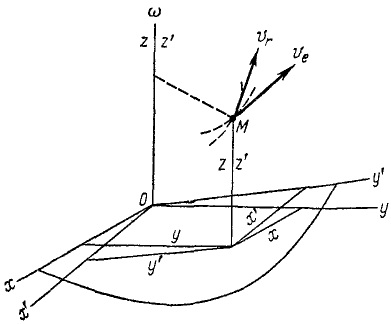
Рис. 121
Пусть подвижная система отсчета вращается вокруг оси Oz основной системы согласно уравнению T==T (О-
Сохраним и в этом параграфе расположение осей координат (см. рис. 101, стр. 165), при котором оси Oz’ и Oz подвижной и неподвижной систем совпадают между собой и с осью вращения, а плоскость х’Оу’ находится в плоскости хОу. Тогда координаты точки M в основной системе определятся соотношениями
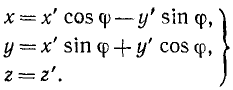
Эти равенства (107) отличаются от уже известных нам равенств (88) тем, что здесь координаты х’, у’ и z’ переменны, тогда как в равенствах (88) они были постоянны.
Если мы мысленно остановим точку M в ее относительном движении, т. е. будем считать ее координаты х’, у’ и z’ постоянными, но сохраним переносное вращение, то, дифференцируя равенства (88) по времени, найдем знакомые нам выражения (89) проекций вращательной скорости, которая в данном случае явится переносной скоростью точки М:
Дифференцируя вторично, найдем проекции переносного ускорения, которые выражаются также известными нам формулами (95):
Чтобы определить относительное движение, мысленно остановим переносное, т. е. будем считать 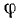
Заметим попутно, что, возводя каждое из этих равенств в квадрат, складывая и извлекая квадратный корень, мы определили бы величину относительной скорости (рис. 122). Если же мы возведем в квадрат и сложим лишь два первых равенства, то, извлекая корень, мы получим, очевидно, величину проекции относительной скорости на плоскость хОу:
Напомним, что вектор угловой скорости 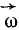
Это соотношение скоро нам понадобится.
Чтобы получить проекции относительного ускорения, надо продифференцировать по времени выражения, полученные для проекций относительной скорости, по-прежнему считая φ постоянной. Имеем
Чтобы определить проекции абсолютной скорости точки М, надо продифференцировать уравнения (107) по времени, считая все величины переменными. Имеем
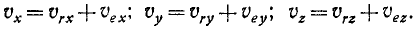
Мы получили теорему параллелограмма скоростей, которая, следовательно, остается в силе и при вращательном переносном движении.
Чтобы определить проекции абсолютного ускорения, возьмем вторые производные, опять-таки считая все величины переменными. Имеем:
Таким образом, в выражениях проекций абсолютного ускорения, вдобавок к проекциям относительного и переносного ускорений, появляется еще одно слагаемое, выражающее проекции добавочного ускорения ac:
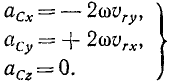
Это добавочное ускорение называют ускорением Кориолиса.
Определим величину ускорения Кориолиса:
или, заменив корень полученным выше значением, находим окончательно
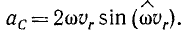
Мы вывели формулу (109) в предположении, что переносное движение вращательное. Она остается без изменений и при всяком ином непоступательном переносном движении.
Итак, если переносное движение не поступательное, то абсолютное ускорение точки равно геометрической сумме трех составляющих: относительного ускорения, переносного ускорения и ускорения Кориолиса:
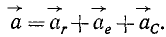
В случае, если переносное движение непоступательное, необходимо дополнить ускорением Кориолиса и схему (105), которая принимает следующий вид:
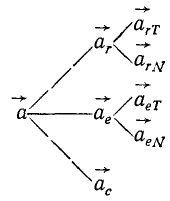
Пользоваться этой схемой при решении задач надо так же, как и схемой (105), заполняя ее справа и геометрически складывая составляющие.
Ускорение Кориолиса существует только при составном движении, если переносное движение непоступательное
При каком движении бывает ускорение Кориолиса
В выражение (109) ускорения Кориолиса входят множителями относительная скорость точки, угловая скорость подвижной системы отсчета и синус угла между векторами этих скоростей. Но относительная скорость бывает только при составном движении. Поэтому и ускорение Кориолиса может быть только при составном движении. Если нет относительной скорости точки, т. е. если υr = 0, то не может быть и ускорения Кориолиса. Однако ускорение Кориолиса бывает не при всяком составном движении точки. Так, если переносное движение поступательное и ω = 0, то нет и ускорения Кориолиса. Из формулы (109) видно, что и в составном движении точки, и при переносном вращательном движении ускорение Кориолиса равно нулю, если относительная скорость параллельна оси вращения. Так, например, корабль, плывущий по меридиану, имеет ускорение Кориолиса, если рассматривать его движение как составное из относительного движения корабля и переносного движения Земли. Это ускорение равно удвоенному произведению скорости корабля на угловую скорость Земли и на синус географической широты (рис. 123) и равнялось нулю в то время, когда корабль пересекал экватор и его относительная скорость была параллельна вектору угловой скорости Земли.
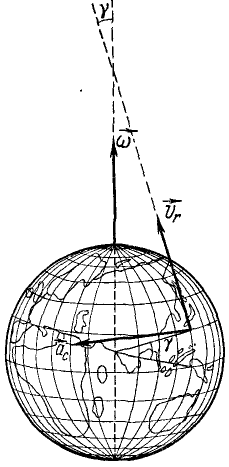
Рис. 123
Физическая причина ускорения Кориолиса заключается в изменении вектора переносной скорости от относительного движения и вектора относительной скорости от переносного движения
Физическая причина ускорения Кориолиса
Постараемся уяснить физические причины, вызывающие ускорение Кориолиса, для чего представим себе два прямолинейных отрезка O1A1 и O2A2 (рис. 124), рис. 123 по которым движутся точки B1 и B2. Штрихами отмечены положения этих отрезков и точек через промежуток времени Δ t. Первый из отрезков движется поступательно, второй вращается вокруг O2.
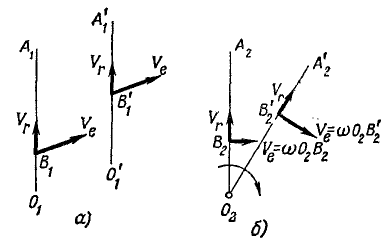
Рис. 124
Существуют две физические причины ускорения Кориолиса:
1. Переносная скорость точки B1 не зависит от положения ее на отрезке O1A1, так как, по свойству поступательного движения, скорости всех точек прямой O1X1 между собой равны. Напротив, величина переносной скорости точки B2 равна ω . O2B2 и всецело зависит от ее положения. Переносная скорость точки B2 меняется от ее относительного движения. Чем быстрее движется точка B2 по прямой O2A2 и чем быстрее вращается эта прямая, тем значительнее изменяется переносная скорость точки B2. Таким образом, изменение скорости точки в данное мгновение (т. е. ускорение точки), вызванное указанной причиной, пропорционально величине агносительной и угловой скоростей. В этом заключается один из факторов, порождающих ускорение Кориолиса.
2. Направление относительной скорости точки B1 не меняется, так как, по свойству поступательного движения, прямая O1A1 передвигается параллельно самой себе. Напротив, направление относительной скорости точки B2 непрерывно изменяется по мере вращения O2А2. Даже при прямолинейном относительном движении направление относительной скорости изменяется (вследствие переносного вращения). Изменение вектора скорости точки в данное мгновение (ускорение), вызванное этой причиной, тоже пропорционально величине относительной и угловой скоростей, В этом заключается другой фактор, порождающий ускорение Кориолиса. Ускорение Кориолиса как бы поворачивает вектор относительной скорости в направлении переносного вращения. По этой причине его иногда называют поворотным ускорением.
Вектор ускорения Кориолиса перпендикулярен векторам угловой и относительной скоростей
Направление ускорения Кориолиса
При выводе формулы ускорения Кориолиса мы убедились, что проекция этого ускорения на Oz равна нулю. Отсюда следует, что вектор ускорения Кориолиса лежит в плоскости, перпендикулярной к оси вращения, или, иными словами, к вектору угловой скорости, который направлен по оси вращения Oz.
Уточним теперь направление ускорения Кориолиса в плоскости, перпендикулярной к осп вращения, и обозначим углы, составляемые им с осью Ox и Оу, через αc и βc. Направляющими косинусами являются:
Углы, составляемые относительной скоростью точки с теми же осями, обозначим через ar и βr:
Сравнивая направляющие косинусы ускорения Кориолиса с направляющими косинусами относительной скорости, находим, что удовлетворяется известное из аналитической геометрии условие перпендикулярности двух направлений—сумма произведений соответствующих направляющих косинусов равна нулю:
следовательно, ускорение Кориолиса перпендикулярно не только к угловой, но и к относительной скорости точки М.
Отсюда вытекает следующее правило: для определения направления ускорения Кориолиса надо спроецировать вектор относительной скорости на плоскость, перпендикулярную Oz (оси вращения), и затем повернуть эту проекцию вокруг оси вращения на 90° в сторону переносного вращения. Следовательно, если переносное вращение происходит в положительном направлении, то проекцию υrxy относительной скорости надо повернуть на 90° против хода стрелки часов, а если переносное вращение происходит в отрицательном направлении, то по ходу стрелки. Это определяется самой сущностью поворотного ускорения, поворачивающего вектор относительной скорости в направлении переносного вращения. К тому же результату мы пришли бы, сравнивая знаки направляющих косинусов ускорения Кориолиса и относительной скорости.
Таким образом, ускорение Кориолиса по величине и направлению можно выразить удвоенным векторным произведением угловой скорости и относительной скорости:
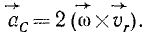
Если относительное движение точки происходит в плоскости, перпендикулярной оси переносного вращения, то угол между векторами угловой и относительной скоростей равен 90°, его синус равен единице и выражение ускорения Кориолиса упрощается:
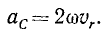
В этом частном, но очень распространенном в технике случае для определения направления ускорения Кориолиса не нужно проецировать вектор относительной скорости точки, а достаточно повернуть его на 90° в плоскости движения точки в сторону переносного вращения. Поясним это следующей задачей.
Пример №7
Стержень OA вращается вокруг оси, перпендикулярной к плоскости чертежа (рис. 125) в точке О. Вдоль стержня движется ползун В. Указать направление ускорения Кориолиса.
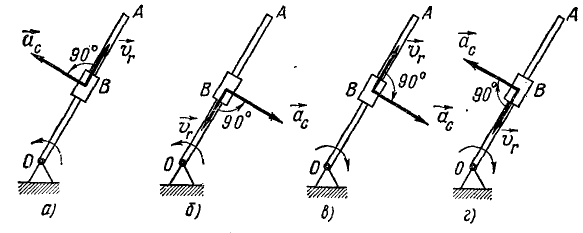
Рис. 125
Решение. Ускорение Кориолиса всегда перпендикулярно к угловой скорости к оси вращения и к относительной скорости. Следовательно, ускорение Кориолиса лежит в плоскости чертежа и перпендикулярно к стержню. Четыре возможных случая изображены на рис. 125, а, б, в, г.
Пример №8
Прямая трубка (рис. 126) равномерно вращается с угловой скоростью ω = π рад/сек вокруг осн Oz, перпендикулярной к плоскости чертежа в точке О. Шарик M совершает гармонические колебания вдоль трубки по закону x’ = ОM = A sin πt. Определить ускорение шарика при t=4 сек.
Решение. Будем рассматривать движение шарика как составное, состоящее из движения относительно трубки и движения вместе с трубкой (рис. 126, а). Для решения задачи воспользуемся схемой (110′) (см. стр. 206).
Чтобы определить относительное движение, мысленно остановим переносное вращение трубки. Уравнение относительного движения шарика есть
В относительном движении шарик имеет касательное ускорение
Относительное движение в данном случае прямолинейное, поэтому относительное нормальное ускорение αrN=0.
Переносное движение обусловлено вращением трубки. Мысленно остановим шарик, предоставив трубке вращаться. Напишем уравнение равномерного вращения трубки, положив φo = 0:
Переносной скоростью шарика является вращательная скорость той точки среды (трубки), в которой в это мгновение находится шарик:
причем в этом выражении время t соответствует тому мгновению, в которое мысленно остановлен шарик, а потому t здесь нельзя рассматривать как переменную величину.
Переносное вращение равномерное, и переносное касательное ускорение равно нулю:
aeT = εr = 0.
Переносное центростремительное ускорение
aeN = ω 2 r — Aπ 2 sin πt,
где t имеет заданное значение, соответствующее данному мгновению, в которое мысленно остановлено относительное движение.
Кроме этих составляющих абсолютного ускорения, имеется ускорение Кориолиса, так как переносное движение вращательное:
Эти составляющие абсолютного ускорения вносим в схему (110′):
В мгновение t = 4 сек имеем:
Таким образом, абсолютное ускорение в это мгновение состоит из ускорения Кориолиса a = ac = 2Aπ 2 .
При t = 4 сек точка M совпадала с точкой О (x’ = A sin 4π = 0) и имела относительную скорость + Аπ, направленную в положительном направлении Ox’. Чтобы определить направление ускорения Кориолиса, надо повернуть вектор относительной скорости на 90° в сторону вращения трубки, т. е. против хода часовой стрелки.
При t = 4 сек угол поворота трубки φ = 4π и ось Ox’ совпадала с осью Ох. Следовательно, в это мгновение ускорение Кориолиса направлено по положительной оси Оу.
Если мы не станем рассматривать движение шарика как составное, а изучим его непосредственно по отношению к основной системе отсчета, то получим, разумеется, тот же результат.
Составим уравнения движения шарика в основной системе координат (рис. 126, б):
Дифференцируя эти уравнения по времени, найдем проекции скорости:
Дифференцируя по времени второй раз, найдем проекции ускорения:
Мы получили те же значения ускорения точки, не пользуясь ускорением Кориолиса. Из этого примера видно, что ускорение Кориолиса бывает лишь при составном движении точки.
Для определения траектории шарика в основной системе отсчета исключим время из уравнений движения. Из второго уравнения находим 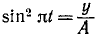
Это уравнение окружности с центром в точке x = 0, 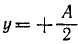
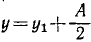
Найдем уравнение движения шарика M по этой окружности:
dx = Аπ cos 2πt dt; dy = Аπ sin 2πt dt;
Следовательно, шарик движется по своей траектории равномерно со скоростью υ= Аπ; при t = 4 сек он находится в наинизшей точке окружности, а нормальное ускорение 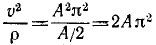
Резюмируя, убеждаемся, что движение шарика (как и движение всякого тела) можно представить различными способами и ускорение шарика в заданное мгновение (t = 4 сек) можно выразить различными формулами.
Можно представить его как составное, состоящее из колебаний шарика вдоль трубки и одновременного вращения трубки. Тогда ускорение 2Аπt 2 шарика в заданное мгновение является ускорением Кориолиса.
Можно представить то же движение шарика уравнениями в декартовых координатах, а ускорение 2Аπt 2 — проекциями на оси координат.
Можно, наконец, это движение шарика определить как равномерное движение со скоростью υ = Аπ по окружности радиуса 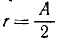
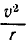
Различные способы лишь выражают объективно существующее движение и позволяют определить его характеристики.
Ответ. a = 2Аπt 2 .
Задача №1
Окружность радиуса г равномерно вращается по ходу стрелки часов с угловой скоростью ω вокруг оси, перпендикулярной к ней в одной из ее точек C (рис. 127, а). По окружности движется точка M со скоростью υr = ωr, обходя окружность против вращения часовой стрелки. Определить ускорение точки М.
Решение. Движение точки будем рассматривать как составное, состоящее из относительного равномерного движения по окружности и переносного равномерного вращения самой окружности.
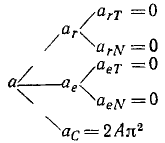
Напишем схему (110′) и будем заполнять ее справа (см. стр. 208).
Чтобы определить относительное движение точки М, мысленно остановим вращение окружности. Относительная скорость равна υr = ωr и направлена по касательной к окружности. Относительное касательное ускорение αrT = 0, а относительное нормальное направлено к центру О окружности и равно
Чтобы определить переносное движение, мысленно закрепим точку M на окружности. Проведем хорду MC (рис. 127, б) и обозначим через δ угол, составляемый ею с диаметром, проходящим через С. Так как окружность вращается равномерно, то αeT = 0 и
αeN = ω 2 CM = ω 2 2r cos δ
и направлено по хорде MC к точке С.
Величина ускорения Кориолиса в нашем случае равна
Переносное вращение происходит по ходу стрелки часов, следовательно, для определения направления ускорения Кориолиса повернем вектор относительной скорости на 90° по ходу стрелки часов.
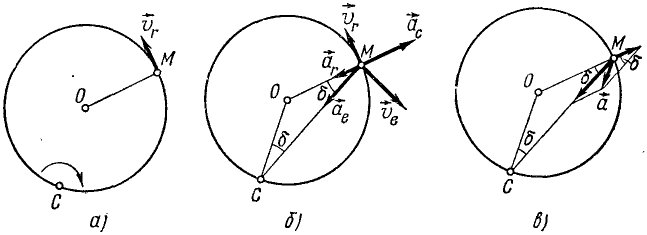
Рис. 127
Скорости и ускорения точки изображены на рис. 127, б, а ускорения записаны по схеме (110′):
Чтобы определить абсолютное ускорение точки М, надо сложить его составляющие. Сложив ускорение Кориолиса с противоположным ему по направлению нормальным относительным ускорением, найдем, что результирующий вектор этих двух ускорений равен ω 2 r и направлен в сторону ускорения Кориолиса:
2ω 2 r-ω 2 r = ω 2 r.
Чтобы сложить этот результирующий вектор с вектором переносного ускорения, воспользуемся теоремой косинусов (рис. 127, в). Имеем
a 2 = (ω 2 r) 2 + (2ω 2 r cos δ) 2 — 2 (ω 2 r) (2ω 2 r cos δ) cos δ = (ω 2 r) 2 .
Как видно из чертежа (рис. 127, в), абсолютное ускорение направлено параллельно ОС независимо от угла δ, т. е. независимо от положения точки M на окружности. Иными словами, независимо от положения точки M на окружности вектор ее абсолютного ускорения равен вектору ускорения центра окружности в его движении вокруг оси С.
Задача №2
В ручке молочного сепаратора по ее длине просверлен цилиндрический канал, закрытый с одной стороны металлической пластинкой (звонком) (рис. 128). В канале помещен металлический шарик. Если вращать ручку с недостаточной скоростью (менее 45 об/мин), то шарик ударится о звонок и даст соответствующий сигнал. Определить ускорение Кориолиса сигнального шарика, если ручка сепаратора наклонена к своей оси вращения под углом 75°, рабочий вращает ручку, делая 45 об/мин, а шарик движется по каналу по закону х’= 220 sin φ + 357e -φ мм.
Решение. Вектор угловой скорости ручки направлен по оси вращения, а относительная скорость шарика —вдоль канала, составляя с ним угол 75°. Ускорение Кориолиса определяем по формуле (105). Угловая скорость 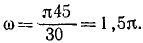
Чтобы определить относительную скорость, надо продифференцировать по времени уравнение движения, в котором φ=ωt=1,5πt.
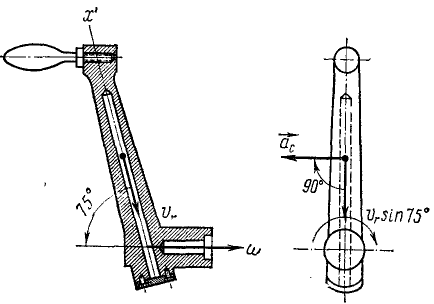
Рис. 128
Таким образом, имеем
αс = 2 • 1, 5π (330π cos φ—535πe — φ) 0,966.
Ответ. Ускорение Кориолиса равно 9420 cos φ—15300e -φ мм/сек 2 и направлено перпендикулярно к ручке и к ее оси.
Видео:Сложное движение точки. Задача 1Скачать

Сложное движение точки и тела
При решении задач, в которых рассматривается сложное движение точки или тела, необходимо уметь правильно расчленить сложное (составное), или так называемое абсолютное движение, на переносное и относительное.
При расчленении сложного движения рекомендуется учитывать следующее. Абсолютное (составное) движение происходит относительно неподвижной системы координат. Обычно эту систему координат связывают с Землей или с неподвижными относительно Земли предметами: зданием, деревом, полотном дороги и т. д.
Переносное движение точки или тела происходит вместе с некоторой материальной средой (телом), внутри или на поверхности которой находится рассматриваемое в задаче тело или рассматриваемая точка. Таким образом, переносное движение — это движение
материальной среды вместе с точкой также относительно неподвижной системы координат.
Относительное движение точки или тела — это перемещение их внутри материальной среды, или по ее поверхности, независящее от движения самой материальной среды.
В тех случаях когда заданы движения двух (или более) тел (точек) относительно неподвижной системы координат и необходимо определить движение одного из этих тел относительно другого, удобно пользоваться теми же приведенными выше соображениями.
Тело, относительно которого требуется рассмотреть движение, мысленно остановим, а неподвижную систему координат заставим двигаться по его закону, но в обратном направлении. Тогда для второго тела это движение станет переносным, а движение второго тела — относительным. После этого очень просто понять, как будет двигаться второе тело по отношению к первому.
Этот последний прием использован при решении задач 177-36 и 184-37 и обычно его используют при рассмотрении планетарных механизмов (см. ниже § 40-9).
Решение всех задач на сложное движение необходимо иллюстрировать рисунком.
Сложение движений точки, когда переносное и относительное движения направлены вдоль одной прямой
При изучении сложного движения точки будем рассматривать только перемещение и скорость.
Если переносное и относительное движения направлены вдоль одной прямой, то:
- перемещение точки в абсолютном движении равно алгебраической сумме перемещений в переносном и относительном движениях;
- скорость точки в абсолютном движении равна алгебраической сумме переносной и относительной скоростей.
Условимся направление переносного перемещения и соответственно направление переносной скорости считать положительными. Тогда относительное перемещение и соответственно относительная скорость будут также положительными, если они направлены в ту же сторону, что и переносное. Если же относительное перемещение (и скорость) имеют направление, противоположное переносному, то будем считать их отрицательными.
Таким образом, при совпадении направлений переносного и относительного движений
При противоположных друг другу направлениях переносного и относительного движений
Задача №3
Вниз по течению реки равномерно плывет лодка, приводимая в движение гребным винтом от мотора. Скорость течения реки 4 км/ч, скорость лодки, сообщаемая ей гребным винтом по отношению к воде, составляет 8 км/ч. Определить скорость лодки относительно берегов и расстояние, которое проходит лодка вдоль берегов за 20 мин.
Решение иллюстрировать рисунком, считая берега реки на данном участке прямолинейными и параллельными.
1. Лодку принимаем за материальную точку, а водную массу реки —за материальную среду.
Движение лодки относительно берегов или, иначе говоря, движение лодки, наблюдаемое с берега, — это абсолютное движение.
Переносное движение лодки—ее перемещение вместе с рекой; скорость 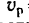
Относительное движение— перемещение лодки по поверхности воды, создаваемое гребным винтом; скорость относительного движения 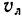
2. Так как в данном случае переносное и относительное движения направлены в одну и ту же сторону, то скорость лодки относительно берегов (абсолютная скорость)
3. За время 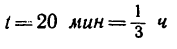
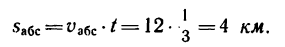
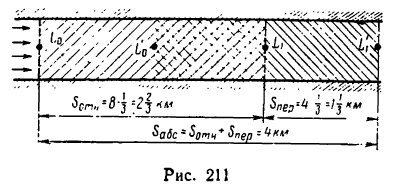
4. Иллюстрируем решение задачи следующим образом (рис. 211).
Изобразим на рисунке тот участок водного пространства, который проходит лодка независимо от того, перемещается этот участок воды или нет. За 20 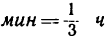
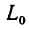
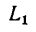
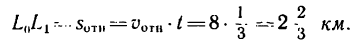
За эти же 20 мин, или
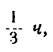
переместится на расстояние
Таким образом, лодка, находившаяся в начале рассматриваемого движения относительно берегов в точке 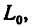
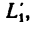
Следовательно, скорость абсолютного движения
Задача №4
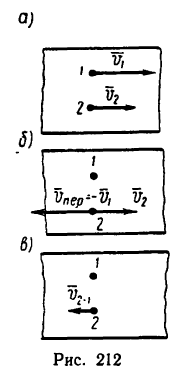
Два автомобиля 1 и 2 движутся параллельно друг другу в одну и ту же сторону со скоростями 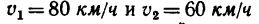
1. Ответ «по соображению» получается мгновенно: 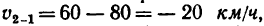
2. Объясним это решение с точки зрения теории сложного движения точки. Условно остановим первый автомобиль. Но тогда, чтобы не изменились условия движения, необходимо мысленно представить, что полотно дороги под вторым автомобилем и вместе с ним получает движение в обратную сторону со скоростью 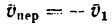
Находясь в условном переносном движении со скоростью 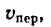
Поэтому результирующая обеих скоростей 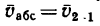
Как видно на рис. 212, а, результирующая направлена в сторону, противоположную скорости
Задача №5
Расстояние s = 90 км между двумя пристанями, расположенными на роке, теплоход проходит без остановки в одном направлении (по течению) за 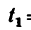
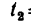
1. Теплоход, который принимаем за материальную точку, двигаясь по течению, имеет абсолютную скорость (скорость относительно берегов):
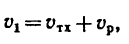
где 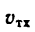
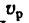
При движении против течения абсолютная скорость теплохода 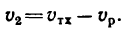
2. Движение теплохода по течению описывается уравнением (рис. 213, а)
Движение теплохода против течения происходит по уравнению (рис. 213, б)
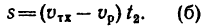
2. Решаем полученную систему уравнения. Из (а) и (б) 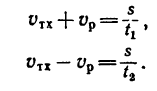
Сложим правые и левые части этих уравнений: 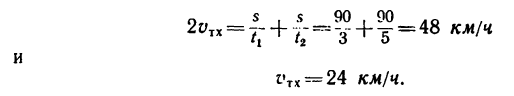
Вычитаем из верхнего равенства нижнее: 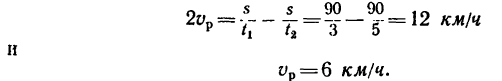
Таким образом, собственная скорость теплохода составляет 24 км/ч и скорость течения реки равна 6 км/ч.
Следующую задачу рекомендуется решить самостоятельно.
Задача №6
Расстояние между двумя пристанями, расположенными на реке, теплоход, двигаясь равномерно без остановки, проходит по течению реки за 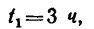
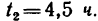
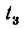
Задачу надо решить в общем виде, а потом подставить числовые значения.
Ответ.
Сложение движений точки, когда переносное и относительное движения направлены под углом друг к другу
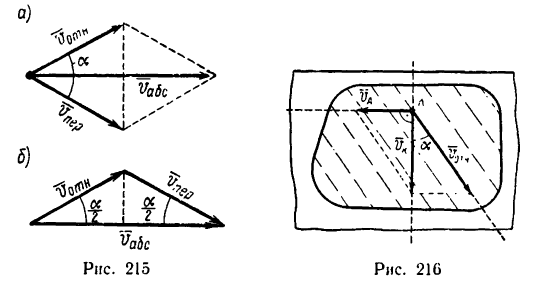
Когда переносное и относительное движения направлены под углом друг к другу, то перемещения и скорости складываются геометрически.
Таким образом, абсолютная скорость точки 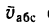
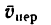
т. е. либо как диагональ параллелограмма, построенного на переносной и относительной скоростях (рис. 214, а), либо как замыкающий вектор треугольника скоростей (рис. 214, б).
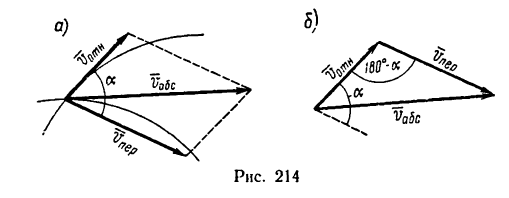
При решении задач на определение скоростей наиболее удобно применять графо-аналитический способ (см. § 3-1 настоящего пособия).
Если применяется правило параллелограмма, то модуль абсолютной скорости определяется по формуле, выведенной из теоремы косинусов
Если применяется правило треугольника, то модуль абсолютной скорости определяется по теореме синусов.
Направление абсолютной скорости по отношению к 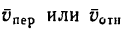
В частном случае, когда параллелограмм скоростей превра шается в прямоугольник или когда треугольник скоростей получается прямоугольным, для решения задачи используются тригонометрические функции и теорема Пифагора (см. ниже задачи 181-37, 182-37, 185-37).
Бели в частном случае 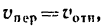
Задача №7
Вертикально падающие капли дождя оставляют на боковых стеклах автомобиля полосы под углом 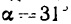
1. Изобразим движение капли дождя на рисунке (рис. 216). Капли падают вертикально, следовательно, скорость ик какой-либо капли К относительно Земли является скоростью абсолютного (составного) движения. И эту скорость 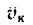
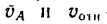
2. Получившийся параллелограмм скоростей диагональ делит на два прямоугольных треугольника. Рассмотрев любой из этих треугольников, найдем
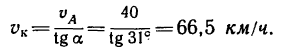
Переводим полученную скорость падения капель в м/сек:
Задача №8
От одного берега реки к другому плывет лодка, держа курс перпендикулярно к берегам. Ширина реки 800 м лодка достигает противоположного берега через 12 мин после начала переправы. За это время лодку сносит вниз по течению на расстояние 600 м. Определить скорость течения реки; собственную скорость лодки: скорость лодки относительно берегов. Скорость течения у берегов и на середине реки считать одинаковой.
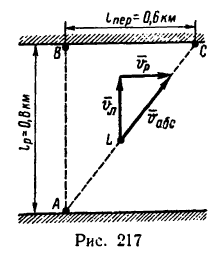
1. Изобразим на рисунке движение лодки (рис. 217). Представим, что лодка отплывает из точки А на правом берегу. Если бы
не было течения, она достигла бы противоположного берега в точке В; известно, что ширина реки 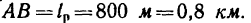
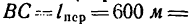
Обозначим точкой L положение лодки через некоторое время после начала движения. Скорость лодки относительно берегов — абсолютная скорость 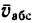
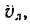
2. Допустим, что нет течения реки, тогда лодка будет перемещаться относительно берегов так же, как и относительно воды, по прямой АВ и ее движение опишется уравнением
где t — время переправы (t=12 мин =0,2 ч).
Отсюда находим собственную скорость лодки (скорость лодки относительно воды — относительную скорость)
3. Если лодка будет плыть, подчиняясь только течению реки, ее движение опишется уравнением
Из этого уравнения найдем скорость течения реки:
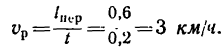
4. Теперь из прямоугольного треугольника скоростей (см. рис. 217) легко найти скорость лодки относительно берегов — абсолютную скорость:
Задача №9
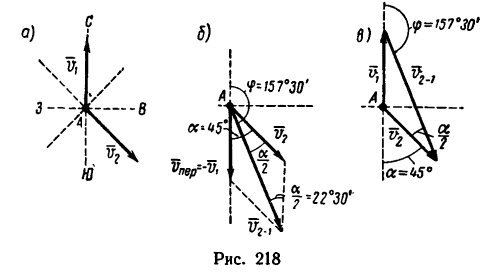
Трассы двух воздушных лайнеров пересекаются над поселком А. Первый лайнер летит точно на север, второй лайнер — на юго-восток. Скорости 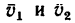
Решение 1—методом «остановки» одного из тел.
1. Обозначим точкой А поселок, над которым» в определенный момент находятся оба лайнера. Покажем страны света: С —север, Ю — юг, В —восток и 3 —запад. Изобразим скорости лайнеров относительно Земли: 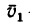
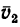
2. Так как нужно определить скорость второго лайнера относительно первого, то мысленно первый лайнер остановим над пунктом А, а воздушной среде вместе со вторым лайнером сообщим скорость 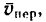
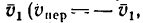
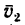
3. Сложив по правилу параллелограмма скорости 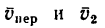
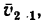
4. Так как скорости лайнеров 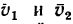
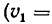
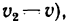
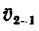
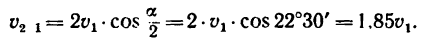
Таким образом, второй лайнер движется относительно первого со скоростью, численно равной и, как видно из рис. 218, б, удаляется от него на юго-юго-запад, т. е. под углом 157°30′ (903 + 45° + 22‘30′) к направлению скорости первого лайнера.
* Когда будет определен этот угол, его нужно сравнить с углом между векторами 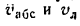
Решение 2 —методом разности скоростей.
1. Из выражения геометрической суммы скоростей
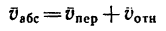
следует, что 
2. Для определения скорости второго лайнера относительно первого примем за абсолютную скорость 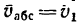
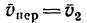
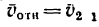
3. Чтобы произвести вычитания векторов, необходимо конец вычитаемого вектора 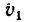
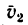
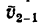
4. В результате построения имеем равнобедренный треугольник скоростей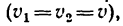
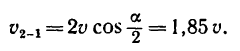
Угол 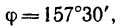
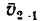
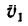
Задача №10
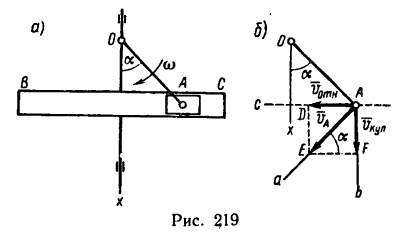
В кривошипно-кулисном механизме с поступательно движущейся кулисой ВС кривошип ОА (расположенный позади кулисы) длиной l= 400 мм вращается с постоянной угловой скоростью 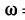
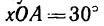
1. В данном случае движение точки А вместе с кривошипом можно считать сложным, т. е. получающимся в результате сложения:
а) движения точки А вместе с кулисой в ее возвратно-поступательном (переносном) движении вдоль оси х;
б) относительного движения точки А вместе с камнем, движущимся возвратно-поступательно в прорези кулисы в направлении, перпендикулярном к оси х.
2. Абсолютная скорость точки А, модуль которой легко определяется по формуле 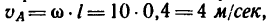
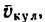
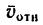
3. Изобразим скорость 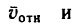
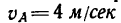
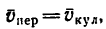
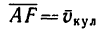
4. 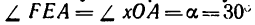
Таким образом, в данный момент кулиса перемещается вниз со скоростью 2 м,сек.
Чтобы лучше проанализировать движение кулисы, необходимо знать, когда кулиса двигается ускоренно, когда замедленно, при каких положениях кривошипа кулиса имеет максимальную скорость и чему равна эта скорость, при каких положениях кривошипа скорость кулисы равна нулю?
Следующие задачи рекомендуется решить самостоятельно.
Задача №11
Кривошип 0С=30 см вращается равномерно с угловой скоростью 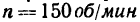
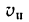
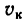
Задача 187-37. Кривошип ОС = 20 см вращается равномерно с угловой скоростью n = 180 об/мин и приводит в движение качающуюся кулису АВ при помощи ползуна С, двигающегося в прорези кулисы. Определить скорость 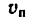
Ответ.
Сложное движение точки в плоскости
постановка задачи. Геометрическая фигура вращается вокруг оси, перпендикулярной ее плоскости по известному закону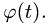
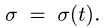
Сложное движение точки М представляется в виде суммы относительного и переносного. Характерной особенностью этой задачи является то, что траектории относительного, переносного и абсолютного движения лежат в одной плоскости. Ось z, на которую проектируются векторы переносной угловой скорости и переносного углового ускорения, перпендикулярна этой плоскости и направлена на наблюдателя. Угол поворота считается положительным, если со стороны оси 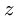
Искомые величины получаем из векторных равенств:
где 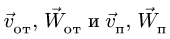
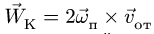
1. Вычисляем значение дуговой координаты 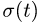
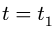
2. Дифференцируя 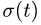
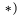
Вектор 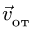
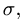
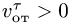
3. Вычисляем радиус траектории переносного движения 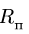
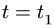
4. Находим переносную скорость 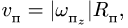
Вектор 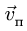
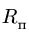
5. Определяем вектор абсолютной скорости, вычисляя компоненты 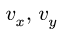
6. Вычисляем относительное ускорение. В случае криволинейной относительной траектории
где
R — радиус кривизны относительной траектории в точке М. Для прямолинейной траектории относительного движения 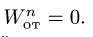
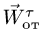
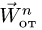
7. Вычисляем переносное ускорение:
Вектор 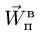
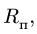
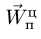
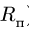
8. Находим ускорение Кориолиса 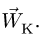
Направление вектора ускорения Кориолиса можно определить по правилу Жуковского 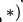
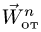
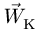
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат. Модуль абсолютного ускорения
Задача №12
Прямоугольник ABCD вращается вокруг оси, проходящей через вершину А, по закон 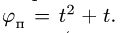
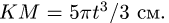
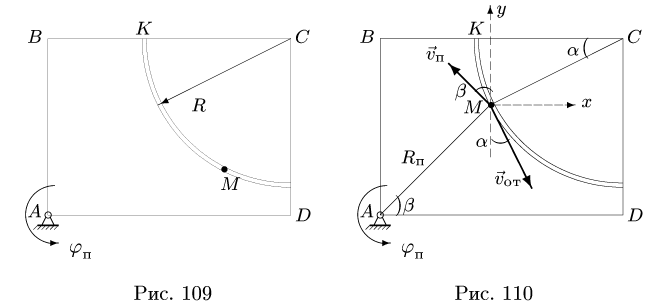
Найти абсолютную скорость и абсолютное ускорение точки М при
Движение точки М представим в виде относительного движения по круговому каналу и переносного движения вместе с вращающимся прямоугольником.
1. Вычисляем значение дуговой координаты 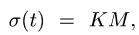
Гл.9.Сложное движение точки
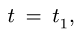
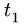
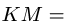
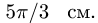
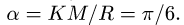
2. Дифференцируя 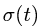
Вектор 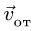
3. Вычисляем радиус траектории переносного движения
4. Находим переносную скорость 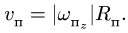
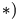
Отсюда
5. Определяем вектор абсолютной скорости по формуле (1). Модуль абсолютной скорости 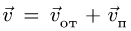
это равенство на неподвижные оси координат х, у (можно воспользоваться также теоремой косинусов):
Тригонометрические функции угла 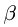
Модуль абсолютной скорости 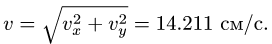
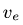
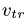
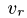
6. Вычисляем относительное ускорение. Ускорение точки, движущейся относительно прямоугольника по окружности, имеет нормальную и тангенциальную составляющую:
Модуль относительного ускорения
Вектор ускорения 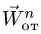
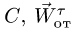
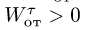
7. Вычисляем переносное ускорение 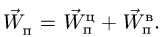
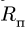
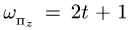
Вектор 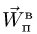
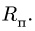
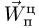
8. Находим ускорение Кориолиса 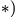
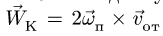
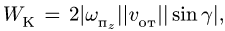
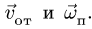
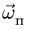
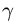
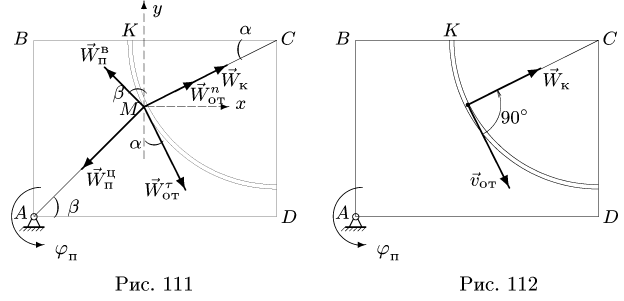
Направление вектора ускорения Кориолиса получаем по правилу Жуковского — поворотом на 90° вектора относительной скорости 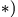
по направлению переносного вращения, т.е. против часовой стрелки (рис. 112).
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат (рис. 111):
Находим модуль ускорения:
Ответы заносим в таблицу. Радиус траектории переносного движения — в см, скорости — в см/с, ускорения — в
Сложное движение точки в пространстве
Постановка Задачи. Геометрическая фигура вращается по заданному закону вокруг неподвижной оси, лежащей в ее плоскости. По каналу, расположенному на фигуре, движется точка М по известному закону 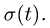
Искомые величины получаем из векторных равенств
где 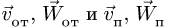
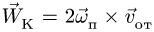
1. Вычисляем значение дуговой координаты 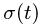
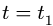
2. Дифференцируя 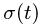
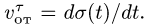
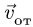
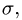
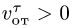
3. Вычисляем радиус траектории переносного движения 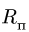
4. Находим модуль переносной скорости 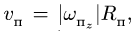
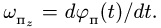
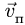
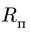
5. Определяем величину абсолютной скорости
6. Вычисляем относительное ускорение. В случае криволинейной относительной траектории
где 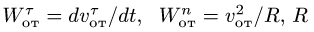
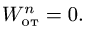
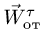
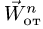
7. Вычисляем переносное ускорение:
Вектор 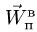
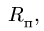
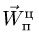
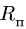
8. Величину вектора ускорения Кориолиса определяем по формуле
Направление вектора ускорения Кориолиса можно определить по правилу Н.Е. Жуковского поворотом на 90° проекции вектора относительной скорости на плоскость, перпендикулярную 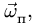
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат. Ось 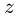
Задача №13
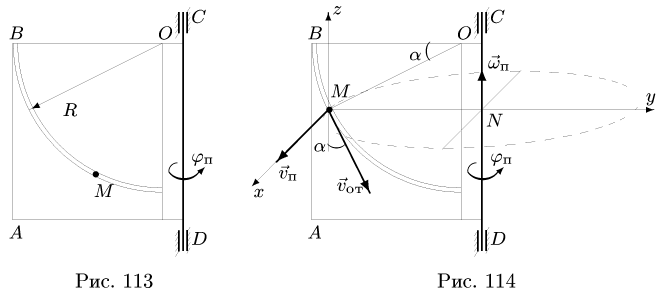
Прямоугольник ABCD вращается вокруг неподвижной оси, проходящей по стороне DC (рис. 113). По круговому каналу радиуса R = 12 см с центром в точке О, расположенному на прямоугольнике, движется точка М по закону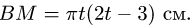
1. Вычисляем значение дуговой координаты 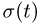
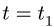
Находим центральный угол, соответствующий дуге ВМ:
Изображаем точку в этом положении (рис. 114).
9.2.Сложное движение точки в пространстве
2. Дифференцируя 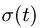
3. Траекторией переносного движения является окружность с центром N. Относительна скорость точки М направлена по касательной к этой окружности. Траектория лежит в плоскости ху, перпендикулярной к оси вращения 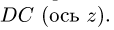
4. Находим переносную скорость. Вычисляем угловую скорость вращения прямоугольника ABCD:
Вычисляем переносную скорость
5. Определяем величину абсолютной скорости. Вектор 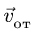
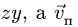
6. Вычисляем относительное ускорение. Находим нормальную составляющую ускорения точки, движущейся по окружности радиуса R:
Оба вектора лежат в плоскости 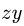
7. Вычисляем компоненты переносного ускорения. Прямоугольник вращается с угловой скоростью 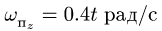
Вектор 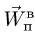
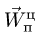
8. Величину вектора ускорения Кориолиса определяем по формуле 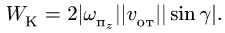
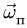
Угол 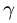
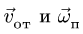
Для того, чтобы найти направление вектора ускорения Кориолиса, воспользуемся правилом Жуковского (рис. 116). Проецируем вектор относительной скорости 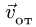
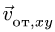
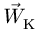
9. Вычисляем абсолютное ускорение по формуле (2) в проекциях на оси координат:
Окончательно, абсолютное ускорение точки М
Ответы заносим в таблицу. Радиус траектории переносного движения — в см, скорости — в см/с, ускорения — в
Движение точки по звену механизма
Постановка Задачи. Плоский шарнирно-стержневой механизм приводится в движение кривошипом, который вращается с заданной угловой скоростью. Вдоль одного из стержней по известному закону движется тючка М. Найти абсолютную скорость и абсолютное ускорение точки М.
Представляем движение точки в виде суммы относительного движения по звену механизма и переносного движения вместе со звеном.
1. Вводим неподвижную систему координат ху, совмещая се начало с положением одного из шарниров механизма в заданный момент времени. Вдоль стержня, по которому движется точка, располагаем подвижную ось 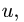
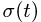
2. Дифференцируя 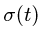
Зная угол между осями 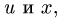
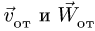
3. Решаем задачу о скоростях точек многозвенного механизма, используя аналитические методы (§ 8.3, с. 179, § 8.5, с. 188). Вычисляем вектор скорости той точки механизма, в которой в данный момент находится подвижная точка М. Эта скорость является переносной скоростью для точки М.
4. Определяем вектор абсолютной скорости, 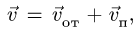
5. Решаем задачу об ускорениях точек многозвенного механизма, используя аналитические методы (§ 8.4, с. 183, § 8.5, с. 188). Вычисляем вектор ускорения той точки механизма, в которой в данный момент находится подвижная точка М. Это ускорение является переносным для точки М.
6. Находим ускорение Кориолиса:
где 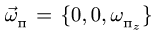
7. Находим абсолютное ускорение, 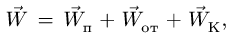
Задача №14
Плоский шарнирно-стержневой механизм ОABC приводится в движение кривошипом OA =60 см, который вращается с постоянной угловой скоростью 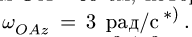
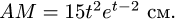
Положение механизма при 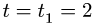
Абсолютное движение точки представляем в виде суммы относительного движения по звену АВ и переносного движения вместе с ним. Переносные скорость и ускорение являются соответственно скоростью и ускорением той точки звена, в которой в данный момент располагается точка М.
1. Вводим неподвижную систему координат ху, совмещая ее начало с положением шарнира А механизма в заданный момент времени. Вдоль стержня АВ, по которому движется точка, располагаем подвижную ось 
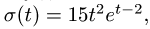
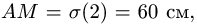
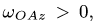
2. Дифференцируя 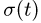
Угол между осями 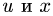
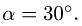
3. Решаем задачу о скоростях точек многозвенного механизма, используя уравнения трех угловых скоростей (§ 8.3, с. 179):
где по условию 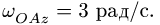
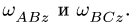
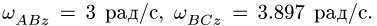
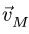
равенства
Переписываем это равенство в виде 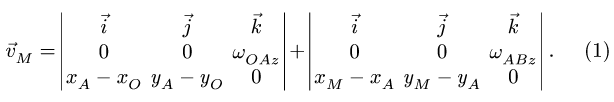
Получаем
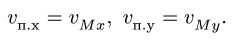
Модуль переносной скорости
4. Определяем проекции.
и модуль абсолютной скорости:
5. Решаем задачу об ускорениях точек многозвенного механизма, используя уравнения трех угловых ускорений (уравнение (2), с. 184), где
Находим 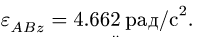
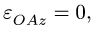
Раскрывая векторные произведения по аналогии с (1), вычисляем
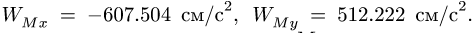
*) Можно выполнить простую геометрическую проверку вычисления 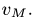
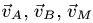
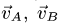
Модуль переносного ускорения
6. Находим ускорение Кориолиса 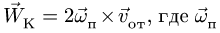
Модуль ускорения Кориолиса
7. Вычисляем абсолютное ускорение
и его модуль
Результаты заносим в таблицу. Скорости в м/с, ускорения — в 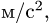
Механизм с муфтой
Постановка Задами. Плоский механизм с одной степенью свободы состоит из шарнирно соединенных стержней и муфты, скользящей по направляющему стержню и шарнирно закрепленной на другом стержне или на неподвижном шарнире. Задана угловая скорость ведущего звена механизма. Найти скорость муфты относительно направляющего стержня.
1. Представляем движение муфты М в виде суммы относительного движения по направляющему стержню механизма и переносного движения вместе с этим стержнем. Траекторией относительного движения муфты является прямая. Задачу решаем, используя координатную запись векторных соотношений для скоростей при плоском движении. Выбираем систему координат и определяем координаты всех шарниров механизма и муфты.
2. Мысленно снимаем муфту с механизма и находим скорости шарниров и угловые скорости звеньев получившегося механизма (§ 8.1, с. 158, § 8.3, с. 179, § 8.5, с. 188).
3. Записываем уравнение сложения скоростей: 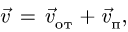
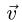
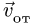
Это векторное уравнение содержит две неизвестные величины. Одна из них — искомый модуль вектора относительной скорости 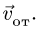
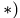
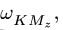
Если муфта скользит по стержню КМ, угловая скорость 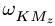
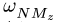
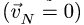
Если муфта шарнирно закреплена на стержне NM с известной угловой скоростью 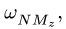
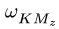
Если муфта закреплена на неподвижном шарнире, то абсолютная скорость равна нулю
3. Решаем векторное уравнение (1). Определяем
Задача №15
Плоский механизм с одной степенью свободы состоит из шарнирно соединенных стержней и муфты D, скользящей по направляющему стержню (кривошипу) OA. Муфта шарнирно закреплена на стержне BD. Кривошип вращается против часовой стрелки с постоянной угловой скоростью 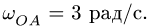
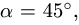
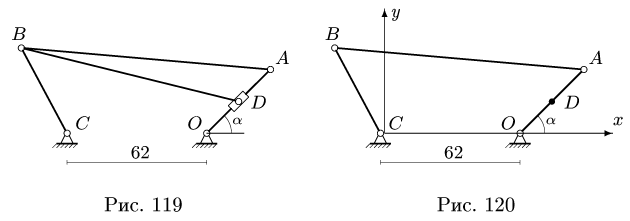
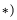
1. Представляем движение муфты М в виде суммы относительного движения по направляющему стержню OA и переносного движения вместе с .этим стержнем. Выбираем систему координат и определяем координаты всех шарниров механизма и муфты. Помещаем начато координат в точку С (рис. 120) и вычисляем координаты:
Координаты точки В найдем из системы уравнений
Система имеет два решения (задача о точках пересечения двух окружностей с радиусами АВ и ВС). Выбираем то решение, у которого
Нелинейную систему уравнений удобно решать на компьютере, например, в системе Maple V. Программа решения имеет вид
Числа заносятся в десятичной форме: АВ: =111.0 и т.д.
2. Мысленно снимаем муфту с механизма (рис. 120) и находим скорости шарниров и угловые скорости звеньев получившегося механизма. Записываем уравнения трех угловых скоростей четырехзвенника ОABC (§8.3, с. 179):
При
Получаем решение: 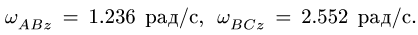
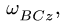
Компоненты скорости имеют следующие значения:
3. Записываем уравнение сложения скоростей 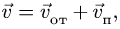
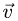
Это уравнение содержит две неизвестные величины. Одна из них — искомый модуль вектора относительной скорости 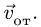
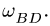
где 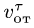
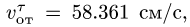
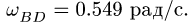
Замечание. Эту задачу можно решить по крайней мере ещё двумя способами. Во-первых, методами аналитической геометрии можно найти расстояние 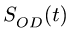
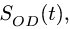
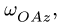
Замечание. В ответах, помимо искомой относительной скорости, даны промежуточные результаты — скорости точек А, Б и D. Причем в вариантах 1,2,7,8 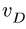
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Сложение движение твердого тела
- Кинематика сплошной среды
- Аксиомы классической механики
- Дифференциальные уравнения движения материальной точки
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Мгновенный центр вращения
- Вращение твердого тела вокруг неподвижной точки
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

iSopromat.ru
Сложным называют движение точки по отношению к двум или нескольким системам отсчета.
Законы Ньютона сформулированы для движения точки по отношению к инерциальным системам отсчета. Для определения кинематических параметров точки при движении относительно произвольно движущейся системы отсчета вводится теория сложного движения.
На рисунке 3.1 показаны:
- условно принимаемая за неподвижную система отсчета O1x1y1z1;
- движущаяся относительно неподвижной система отсчета Oxyz;
- точка M, перемещающаяся по отношению к подвижной системе отсчета.
Движение точки M в данном случае является сложным. Её движение по отношению к подвижной системе отсчета называют относительным движением.
Движение той точки подвижной системы отсчета, в которой в данный момент находится движущаяся точка, по отношению к неподвижной системе отсчета называют переносным движением. Движение точки M по отношению к неподвижной системе отсчета называют абсолютным движением.
По аналогии с этими определениями будут называться относительные, переносные и абсолютные скорости и ускорения точки. Для их обозначения в относительном движении часто всего используется индекс r (relative – относительный) — Vr , ar; в переносном движении индекс e (entrained — увлекать за собой) — Ve , ae.
Ниже приведен пример сложного движения точки — M.
На рисунке 3.2,а показан квадрат, вращающийся в плоскости чертежа вокруг неподвижной точки. По стороне квадрата движется точка M. Она участвует в двух движениях, поэтому можно ввести две системы отсчета: неподвижную, например, O1x1y1z1 — по отношению к которой вращается квадрат и подвижную Oxyz, скрепленную с квадратом, по оси Oy которой движется точка M (рисунок 3.2,б).
Движение точки M по стороне квадрата (по оси Oy скрепленной с квадратом подвижной системы) является относительным — скорость в этом движении Vr.
Вращение точки M вместе с квадратом — переносное движение, скорость в этом движении — Ve. Абсолютное движение является результатом сложения переносного и относительного движений.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
🎥 Видео
Кинематика. 4.3. Сложное движение точки на примере диска. Определение абсолютной скорости точки.Скачать

Сложное движение точки. Часть 1Скачать

Кинематика точки Движение по окружностиСкачать
Сложное движение точкиСкачать

Сложное движение точки #2Скачать

Физика - движение по окружностиСкачать

Сложное движение точки #3Скачать

Ускорение Кориолиса. Авторы: Шабалин Руслан, Швецов ВиталийСкачать

Сложное движение точки, Леннаучфильм, 1978Скачать

Термех. Сложное движение точки. Определение абсолютной скорости и ускорения.Скачать

Определение абсолютной скорости и абсолютного ускорения точкиСкачать
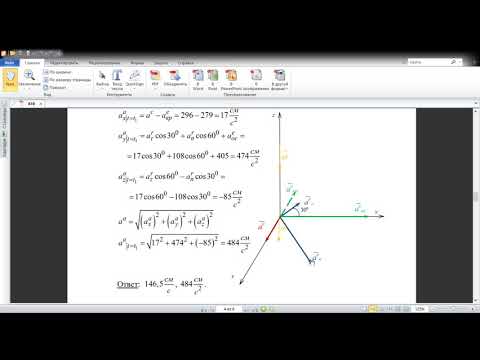
Вращательное движение. 10 класс.Скачать

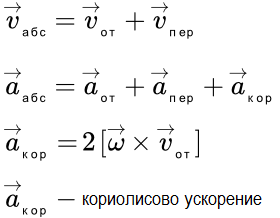
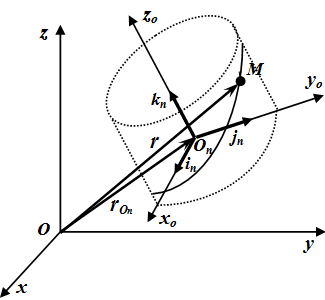
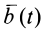
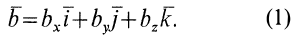
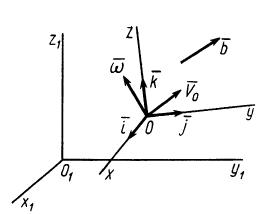
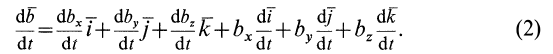
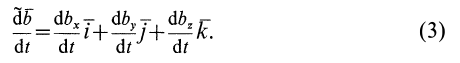
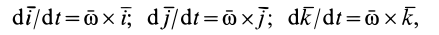
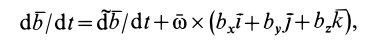
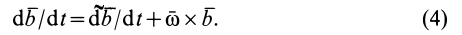
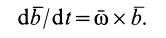
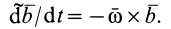
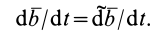
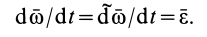
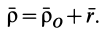
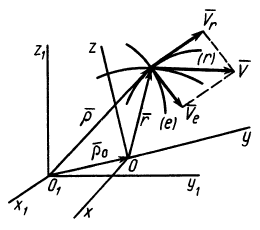
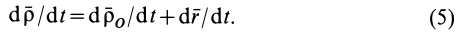
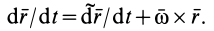

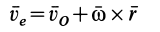

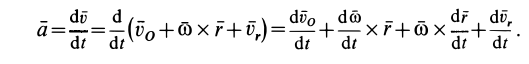
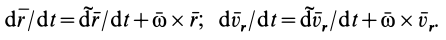
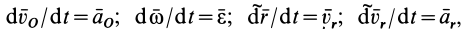
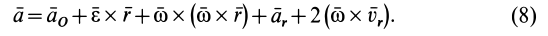


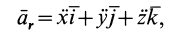
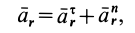
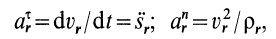
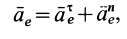
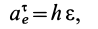
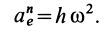
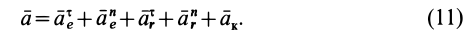
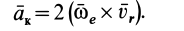
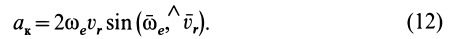
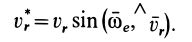

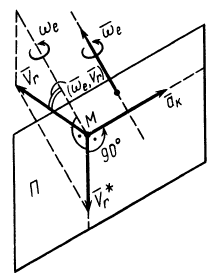
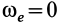 , т. е. переносное движение является поступательным;
, т. е. переносное движение является поступательным;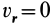 , т. е. в те моменты времени, в которые происходит изменение направления относительного движения;
, т. е. в те моменты времени, в которые происходит изменение направления относительного движения;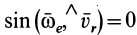 , т. е. когда скорость относительного движения
, т. е. когда скорость относительного движения 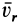 параллельна угловой скорости переносного вращения
параллельна угловой скорости переносного вращения 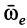 .
.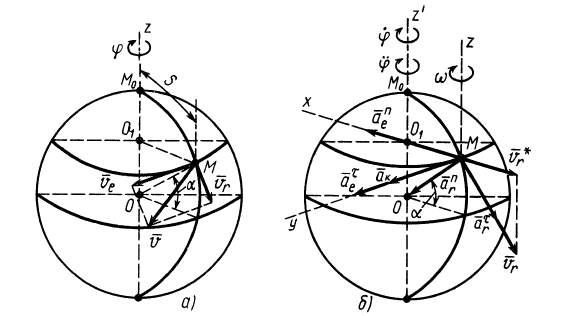
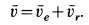
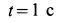
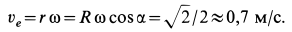
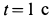
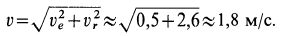

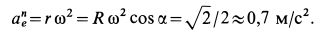
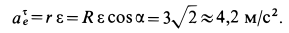
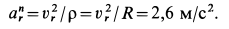
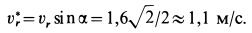
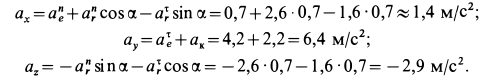
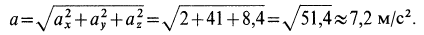
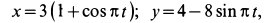
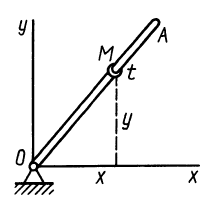
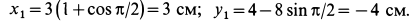
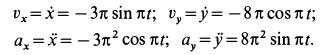
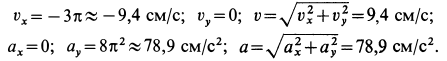
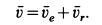
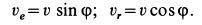
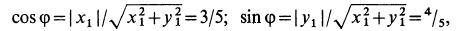
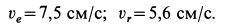
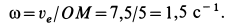
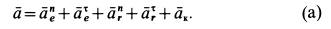
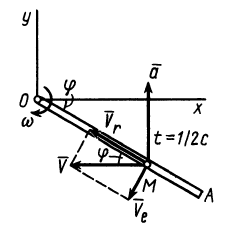
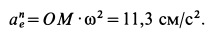
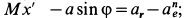
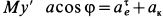 .
.