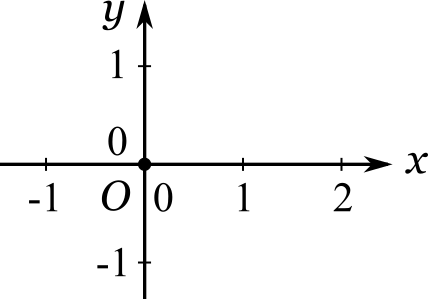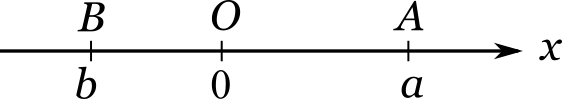Сложение векторов в полярной системе координат (5 видео)

4.11. Координаты и векторы

Прямоугольная декартова система координат

Рассмотрим на плоскости числовую прямую (x) с началом отсчета в точке (O) . Повернем эту прямую вокруг точки (O) на угол (+90°) и обозначим ее новое положение через (y) (мы поставили знак плюс перед значением угла, чтобы подчеркнуть, что поворот осуществляется в положительном направлении, то есть против часовой стрелки). Первоначальное положение числовой прямой мы, однако, не исключаем из нашего рассмотрения и сохраняем за ним прежнее обозначение (x) .

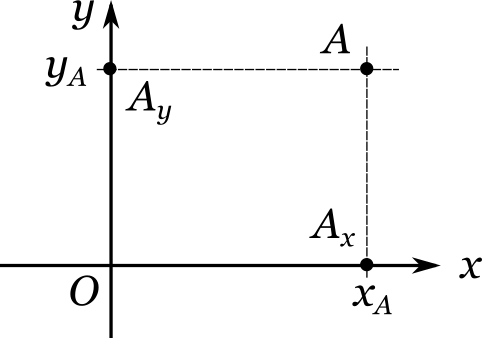
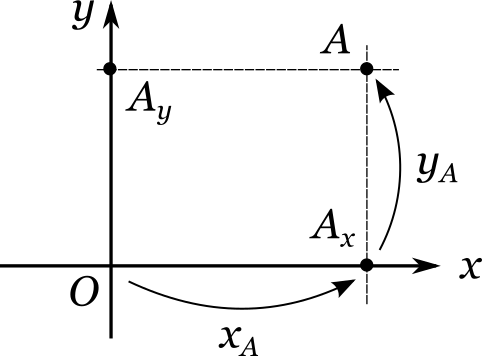
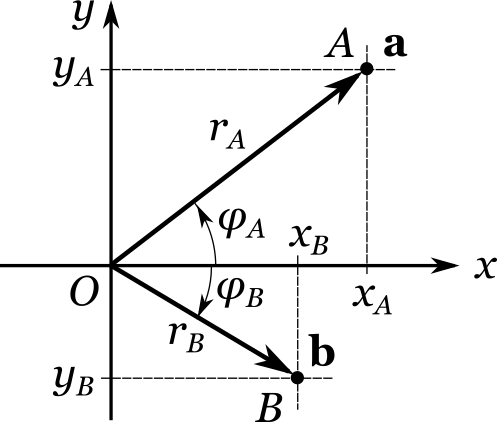
Полученная конструкция носит название прямоугольной системы координат. Иногда ее также называют декартовой системой координат (в честь французского математика Рене Декарта). С ее помощью очень удобно задавать положение любой точки на плоскости. Действительно, возьмем произвольную точку (A) и опустим из нее перпендикуляр на каждую из прямых (x) и (y) . Обозначим соответствующие точки пересечения через (A_x) и (A_y) . Они называются проекциями точки (A) на оси (x) и (y) . Пусть положение точки (A_x) вдоль числовой прямой (x) характеризуется числом (x_A) , а положение точки (A_y) вдоль прямой (y) — числом (y_A) . Тогда пара чисел ((x_A, y_A)) называется прямоугольными (или декартовыми) координатами точки (A) .

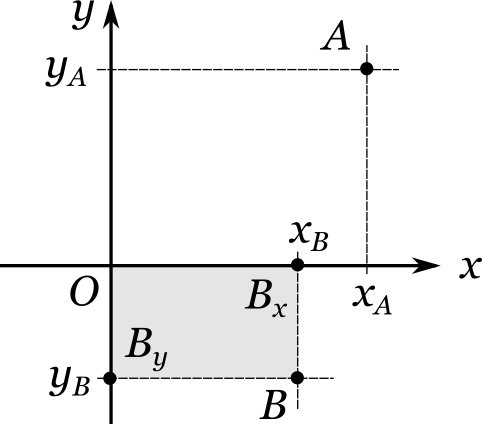
Теперь допустим, что нам даны два произвольных действительных числа (x_B) и (y_B) и известно, что они являются декартовыми координатами некоторой точки (B) . По этим данным мы теперь легко можем найти саму точку (B) . Вначале найдем ее проекции: отметим на оси (x) точку (B_x) , положение которой вдоль этой оси задается числом (x_B) , а на оси (y) отметим точку (B_y) , положение которой задается числом (y_B) . Затем проведем через проекции (B_x) и (B_y) прямые, параллельные соответственно осям (y) и (x) :

У нас получился параллелограмм. Его вершина, расположенная напротив вершины (O) , и есть, очевидно, искомая точка (B) .

Плоскость, снабженная прямоугольной системой координат, называется координатной плоскостью. Мы только что выяснили, что между точками координатной плоскости и парами действительных чисел существует взаимно-однозначное соответствие: каждой точке (A) соответствует строго определенная координатная пара ((x_A, y_A)) , а каждой координатной паре ((x_B, y_B)) соответствует строго определенная точка (B) . Тут всё очень похоже на то, как устроена числовая прямая — с той только разницей, что для задания точки на числовой прямой требуется одно действительное число, а для задания точки на координатной плоскости требуется два действительных числа. По этой причине прямую иногда называют одномерным пространством, а плоскость — двухмерным пространством.

Отметим, что порядок следования чисел в паре координат имеет принципиальное значение: так, координаты ((1, 2)) задают вовсе не ту же самую точку, что и координаты ((2, 1)) . Первая координата в паре ((x_A, y_A)) называется абсциссой, а вторая — ординатой. В соответствии с этим, прямую (x) часто называют осью абсцисс, а прямую (y) осью ординат. Точка пересечения координатных осей, обозначаемая обычно буквой (O) , называется началом координат. Вместо слов «точка (A) с координатами ((x_A, y_A)) » часто пишут просто «точка (A(x_A, y_A)) » или же, еще короче, «точка ((x_A, y_A)) ».

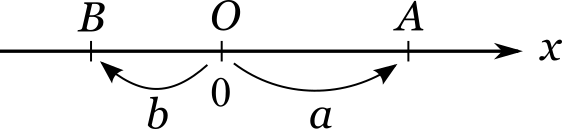
Давайте начертим числовую прямую с началом отчета в точке (O) и рассмотрим ее хорошенько:

Здесь возле одних и тех же засечек по одну сторону от прямой стоят обозначения точек (O) , (A) и (B) , а по другую сторону — соответствующие им числа (0) , (a) и (b) . Чем же числа отличаются от точек? Отличие состоит в том, что число — это не сама точка, а скорее краткая инструкция, как найти ее местоположение. Числовую прямую правильнее было бы рисовать следующим образом:

Обычно так не рисуют лишь по той причине, что чертеж в этом случае получается более громоздким. Число (a) описывает смещение, переводящее точку (O) в точку (A) , и тем самым задает положение точки (A) на числовой прямой. Это смещение может быть как положительным, так и отрицательным. Принципиальным моментом тут является то, что числа можно складывать между собой, а точки — нельзя.

В случае координатной плоскости дело обстоит очень похожим образом, только вместо чисел здесь фигурируют координатные пары. Координаты ((x_A, y_A)) можно рассматривать как инструкцию для определения местонахождения соответствующей точки (A) . Для этого надо встать в начало координат, точку (O) . Затем сделать (x_A) единичных шагов в том направлении, в котором указывает ось (x) (если число (x_A) отрицательно, то фактически движение осуществляется в противоположном направлении), а после этого сделать (y_A) единичных шагов в направлении, в котором указывает ось (y) . В результате мы оказываемся в точке (A) .

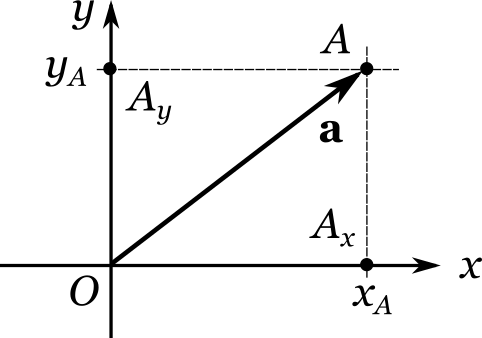
((x_A, y_A)) , — которая описывает смещение, переводящее точку (O) (начало координат) в точку (A) .—>Однако же, когда речь идет о координатной плоскости, вместо слова «инструкция» более принято употреблять другое слово, а именно вектор. На чертежах, во избежание излишней громоздкости, векторы изображают не в виде двух отдельных шагов, как это мы сделали выше, а в виде одного прямолинейного отрезка-стрелки:

Векторам часто присваивают буквенное обозначение. Вектор () , соответствующий точке (A) , имеет те же координаты ((x_A, y_A)) , что и сама точка. Применительно к векторам координаты также называют компонентами. Между вектором и парой его компонентов можно ставить знак равенства: ( = (x_A, y_A)) . Букву, обозначающую вектор, обычно выделяют на печати полужирным шрифтом, чтобы его нельзя было спутать с обычным числом. В рукописных текстах, где применение полужирного шрифта было бы не слишком практичным, над обозначением вектора принято ставить стрелочку: (vec a) . Иногда для лучшего зрительного восприятия координаты вектора записывают в столбик:

Заметим, что понятия координат и векторов применимы, в принципе, и в случае, когда мы рассматриваем одномерную числовую прямую: положение точки на прямой часто называют ее одномерной координатой, а смещение вдоль прямой является фактически одномерным вектором. Одномерная координата, как и одномерный вектор — это обычные действительные числа.

Полярная система координат

Представим себя на месте человечка, которому надо добраться из начала координат (O) в некоторую точку (A(x_A, y_A)) . В этой ситуации инструкция, записанная в виде декартовых координат, нас бы, наверное, не очень обрадовала. Ведь если мы вначале будем идти в направлении оси (x) , а потом в направлении оси (y) , то мы проделаем не самый близкий путь. Нет уж, — скажем мы, — вы лучше с самого начала укажите нам точное направление на точку (A) и сообщите, сколько шагов надо сделать: так-то мы доберемся быстрее.

Что ж, такая возможность тоже имеется.

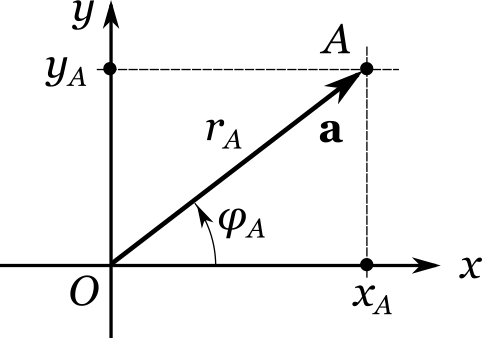
Направление можно задать, например, с помощью углового смещения (varphi_A) , отсчитываемого от положительного направления оси (x) . Величина (varphi_A) носит название полярного угла или полярной координаты. Число шагов — это не что иное, как расстояние (r_A) между началом координат и точкой (A) . Иначе говоря, (r_A = |OA|) . Величину (r_A) называют иногда радиальной координатой. Новая инструкция записывается в виде пары ((r_A, varphi_A)) , которая называется полярными координатами точки (A) .

Мы, однако же, договорились вместо слова «инструкция» говорить «вектор». Таким образом, вектор () , соответствующий точке (A) , — это совокупность направления, задаваемого углом (varphi_A) , и расстояния (r_A) , которое надо проделать в этом направлении.

Но мы еще совсем недавно отождествляли вектор () с парой декартовых координат ((x_A, y_A)) . Что же такое вектор на самом деле? Тут важно то, что обе инструкции — как «декартова» ((x_A, y_A)) , так и «полярная» ((r_A, varphi_A)) , — хотя и отличаются в деталях, описывают одно и то же смещение, и в этом смысле они являются разными представлениями одного и того же вектора () . Впрочем, во избежание путаницы, знак равенства между вектором () и его полярными координатами ((r_A, varphi_A)) писать не принято.

Заметим, что если (r_A = 0) , то полярному углу (varphi_A) можно приписать любое значение. В остальных случаях, как нетрудно убедиться, между точками на плоскости и их полярными координатами имеется взаимно-однозначное соответствие. А значит, полярные и декартовы координаты также связаны между собой взаимно-однозначным соответствием: по полярным координатам можно единственным образом восстановить декартовы, и наоборот, по декартовым координатам можно единственным образом восстановить полярные.

Сложение и вычитание векторов

Смещение, инструкция о котором записана в векторе, можно, разумеется, применить не только к началу координат (O) , но и вообще к произвольной точке, лежащей на плоскости. Пусть нам даны два вектора () и () , соответствующие точкам (A) и (B) .

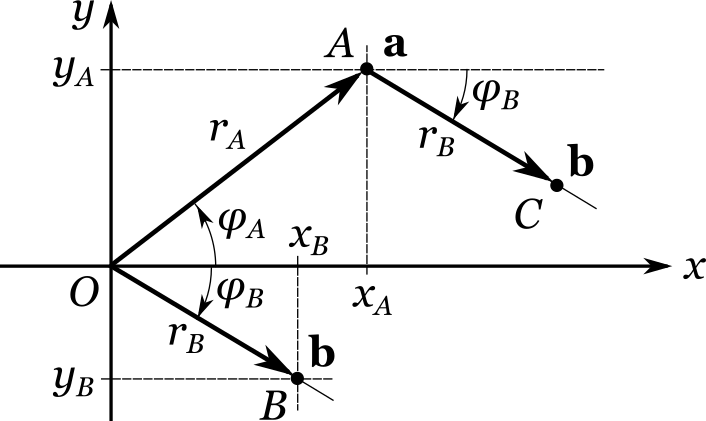
Сместим точку (A) в соответствии с инструкцией, заложенной в векторе () . Но в нашем распоряжении две инструкции — «декартова» ((x_B, y_B)) и «полярная» ((r_A, varphi_A)) . Какой лучше воспользоваться? Если мы ищем графическое решение с помощью чертежа, то «полярная» инструкция оказывается удобнее.

Из исходной точки (A) проведем луч параллельно лучу (OB) и пройдем по нему расстояние, равное длине отрезка (OB) . Мы попадем в некоторую точку (C) , которая, собственно, и является результатом проделанного смещения. Однако если мы теперь захотим рассчитать ее полярные координаты, то обнаружится, что это очень непростая задача. Попробуем проделать то же самое смещение, следуя «декартовой» инструкции.

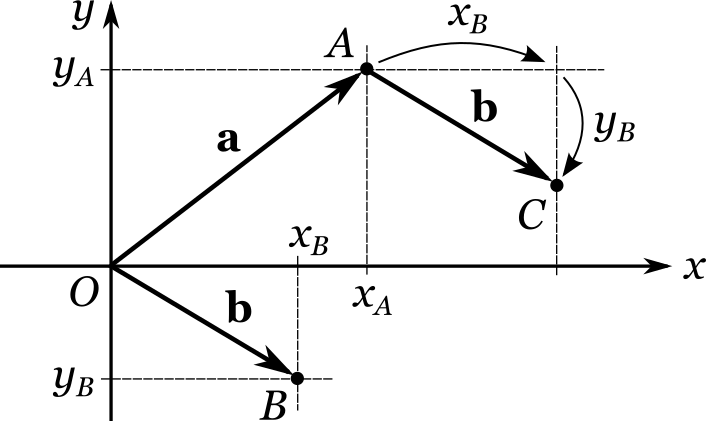
Для этого, исходя из точки (A) , сделаем (x_B) шагов в направлении оси абсцисс и (y_B) шагов в направлении оси ординат (опять-таки, если число шагов отрицательно, движение фактически осуществляется в противоположную сторону). Поскольку инструкции по сути эквивалентны, мы окажемся всё в той же точке (C) . Однако, так как на этот раз мы имеем дело с декартовыми координатами, вычислить их не составляет труда.

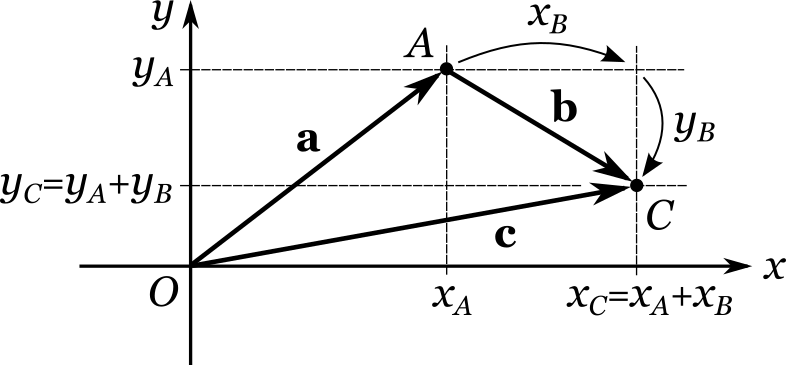
Как хорошо видно из рисунка, точке (C) соответствует вектор

В таких случаях говорят, что вектор () является суммой векторов () и () :

Вместе с тем, координаты вектора () можно представить в виде

Вектор () естественно назвать разностью векторов () и () :

Чтобы хорошенько запомнить определения суммы и разности векторов, выпишем их еще раз, обведя в рамку:

Вектор ( — = big(beginx_C — x_A\y_C — y_Aendbig)) , переводящий точку (A) в точку (C) , принято также обозначать как (overrightarrow) . В этих обозначениях определение сложения и вычитания принимает вид:

(begin overrightarrow = overrightarrow + overrightarrow,\ overrightarrow = overrightarrow — overrightarrow. end)

Здесь под точкой (O) подразумевается, как и прежде, начало координат, но данные равенства, разумеется, сохранятся, если ее заменить на любую другую точку (D) :

(begin overrightarrow = overrightarrow + overrightarrow,\ overrightarrow = overrightarrow — overrightarrow. end)

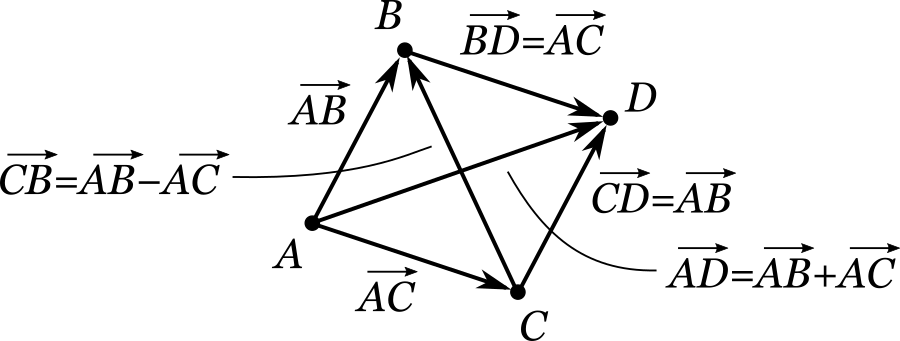
Задача () Пусть на координатной плоскости заданы три точки (A) , (B) и (C) . Изобразить в виде отрезков-стрелок векторы ( overrightarrow + overrightarrow ) и ( overrightarrow — overrightarrow ) .

Одно из возможных решений представлено на рисунке.

Для нахождения разности нам не понадобилось делать никаких дополнительных построений: оказалось достаточным просто соединить имеющиеся точки (C) и (B) . Для нахождения же суммы пришлось построить дополнительную точку (D) , такую чтобы четырехугольник (ACDB) представлял собой параллелограмм.

Очевидно, что сложение векторов обладает свойствами коммутативности и ассоциативности:

На практике это означает, что суммирование большого числа векторов можно производить в любой последовательности. Также естественно считать, что

Вообще, умножение вектора ( = (x_a, y_a)) на произвольное действительное число (k) определяется как

В частности, для всякого вектора ( = (x_a, y_a)) определен противоположный ему вектор, равный

Для векторов, переводящих точку (A) в точку (B) и обратно, справедливо равенство

Как несложно убедиться,

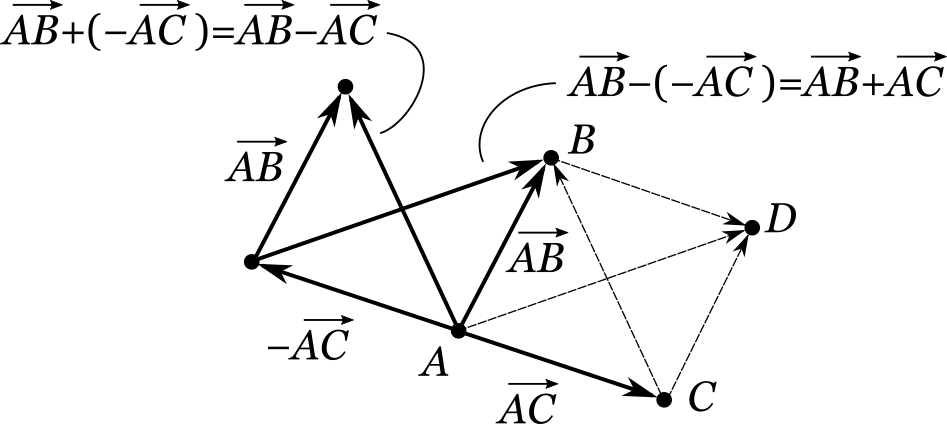
На основании этих равенств мы можем предложить еще одно решение рассмотренной ранее задачи (4.11.1) , в которой требовалось по заданным точкам (A) , (B) и (C) построить векторы ( overrightarrow + overrightarrow ) и ( overrightarrow — overrightarrow ) :

Отметим также, что умножение вектора на число обладает свойством дистрибутивности:

Это легко проверить непосредственно с помощью определений, по которым производятся операции с векторами.

Переход между разными системами прямоугольных координат

Мы рассмотрели случай, когда на плоскости задана одна единственная прямоугольная система координат. Но на самом деле таких систем может быть сколь угодно много.

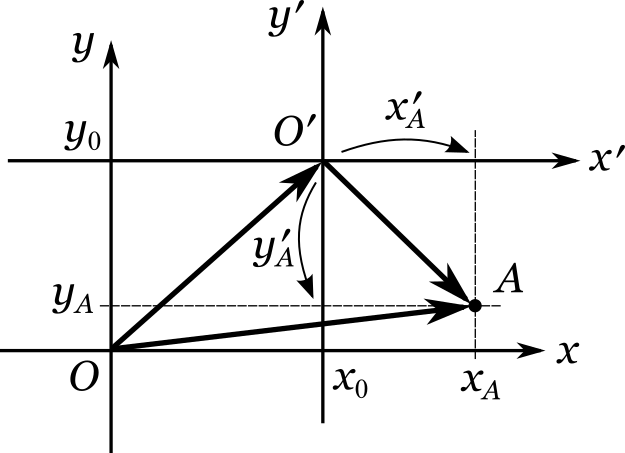
Задача () Пусть на плоскости заданы две прямоугольные системы координат. Первая — с началом в точке (O) и осями (x) и (y) . Вторая — с началом в точке (O’) (читается: «о-штрих») и осями (x’) и (y’) , причем ось (x’) сонаправлена с осью (x) первой системы. Координаты точки (A) в первой системе равны ((x_A, y_A)) . Каковы ее координаты ((x_A’, y_A’)) во второй системе, если изветно, что (overrightarrow = (x_0, y_0)) ?

Координаты точки (A) в первой системе, очевидно, совпадают с координатами вектора (overrightarrow) , а координаты этой же точки во второй системе совпадают с координатами вектора (overrightarrow) . Эти векторы связаны между собой соотношением

(overrightarrow = overrightarrow + overrightarrow) или же (overrightarrow = overrightarrow — overrightarrow) .

Отсюда получаем ответ:

(beginx_A’\y_A’end = overrightarrow = begin x_A \ y_A end — begin x_0 \ y_0 end = beginx_A — x_0\y_A — y_0end ) .

Запомним этот результат хорошенько, потому что нам предстоит часто использовать его в будущем.

Конспект

(1) . Система прямоугольных координат на плоскости: две числовые оси (x) и (y) , расположенные так, что ось (y) повернута относительно оси (x) на (+90°) и начала отсчета обеих осей совпадают с точкой пересечения (O) .

(2) . Если построить проекции произвольной точки (A) на числовые прямые (x) и (y) , то их положение на этих прямых будет характеризоваться некоторыми числами (x_A) и (x_B) , соответственно. Пара чисел ((x_A, y_A)) носит название прямоугольных координат точки (A) . Первая координата в паре ((x_A, y_A)) называется абсциссой, а вторая — ординатой.

(3) . Полярные координаты ((r_A, varphi_A)) точки (A) : если мы находимся в начале координат (O) , то это — во-первых, расстояние (r_A = |OA|) до точки (A) , а во-вторых, направление на эту точку (иначе говоря, направление луча (OA) ), которое задается угловым смещением (varphi_A) , отсчитываемым от оси (x) .

(4) . Вектор ( = overrightarrow) : инструкция по перемещению начала координат (O) в точку (A) , которая может быть задана как в виде прямоугольных координат ( = big(beginx_A\y_Aendbig)) , так и в виде полярных координат ((r_A, varphi_A)) . Применима не только к точке (O) , но и к любой другой точке (B) . Если при этом точка (B) перемещается в точку (C) , то это записывают как (overrightarrow = overrightarrow = ) .

(5) . Пусть координаты векторов ( = big(beginx_a\y_aendbig)) , ( = big(beginx_b\y_bendbig)) и ( = big(beginx_c\y_cendbig)) связаны между собой соотношением

Тогда вектор () называетеся суммой вектров () и () , а вектор () — разностью векторов () и () :

(6) . Для любых трех точек (A) , (B) и (C) справедливо:

(overrightarrow = overrightarrow + overrightarrow) ,

(overrightarrow = overrightarrow — overrightarrow) .

(8) . Свойства сложения и вычитания векторов похожи на свойства сложения и вычитания чисел:

(9) . Преобразование прямоугольных координат при переходе в новую систему: если оси обоих систем сонаправлены, а начало новой системы сдвинуто относительно старой на вектор (big(beginx_0\ y_0endbig)) , то новые координаты (big(beginx_A’\ y_A’endbig)) точки (A) выражаются через старые (big(beginx_A\ y_Aendbig)) как (big(beginx_A’\y_A’endbig) = big(beginx_A — x_0\y_A — y_0endbig)) .

Содержание

Полярная система координат: основные понятия и примеры
Полярная система координат: основные понятия и обозначения
Связь полярных координат с декартововыми координатами
Задачи о точках в полярной системе координат
Полярная система координат (полярные координаты)
🎬 Видео

Видео:Сложение и вычитание векторов через координаты. Практическая часть. 11 класс.Скачать

Полярная система координат: основные понятия и примеры

Видео:Полярная система координатСкачать

Полярная система координат: основные понятия и обозначения

Если уж речь зашла о полярной системе координат, то вообразите себя полярниками, стоящими на Северном полюсе. Или на Южном (это не так важно). Пусть в точке полюса находится начало линейки. В точку полюса также положим начало карандаша, а весь карандаш полностью прилегает к линейке. Теперь повернём карандаш так, чтобы его начало оставалось там же, на полюсе, а между ним и линейкой образовался некоторый угол поворота. Конец карандаша оказался в некоторой точке, назовём её M. Вот мы и получили полярные координаты точки M: длина карандаша и угол, на который был повёрнут карандаш. А теперь об этом же в более строгих и точных определениях.

Полярная система координат определяется заданием некоторой точки O, называемой полюсом, исходящего из этой точки луча OA (обозначается также и как Ox), называемого полярной осью, и масштаба для изменения длин. Кроме того, при задании полярной системы координат должно быть определено, какие повороты вокруг точки O считаются положительными (на чертежах обычно положительными считаются повороты против часовой стрелки).

Итак, выберем на плоскости (рисунок выше) некоторую точку O (полюс) и некоторый выходящий из неё луч Ox. Кроме того, укажем единицу масштаба. Полярными координатами точки M называются два числа ρ и φ, первое из которых (полярный радиус ρ) равно расстоянию точки M от полюса O, а второе (полярный угол φ, который называют также амплитудой) — угол, на который нужно повернуть против часовой стрелки луч Ox до совмещения с лучом OM.

Точку M с полярными координатами ρ и φ обозначают символом M(ρ, φ) .

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Связь полярных координат с декартововыми координатами

Установим связь между полярными координатами точки и её декартовыми координатами. Будем предполагать, что начало декартовой прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью. Пусть точка M имеет декартовы координаты x и y и полярные координаты ρ и φ.Тогда

Полярные координаты ρ и φ точки M определяются по её декартовым координатам следующим образом:

Для того, чтобы найти величину угла φ, нужно, используя знаки x и y, определить квадрант, в котором находится точка M, и, кроме того, воспользоваться тем, что тангенс угла φ равен .

Приведённые выше формулы называются формулами перехода от декартовых координат к полярным.

Одно из наиболее частых применений полярных координат в высшей математике — решения двойных интегралов в полярных координатах.

Видео:Сложение и вычитание векторов через координаты. Практическая часть. 11 класс.Скачать

Задачи о точках в полярной системе координат

Пример 1. В полярной системе координат на плоскости даны точки

Найти полярные координаты точек, симметричных этим точкам относительно полярной оси.

Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полярной оси точки будет как и у данной точки. Как видно из рисунка в начале урока, при построении симметричной относительно полярной оси точки данную точку нужно повернуть вокруг полярной оси на тот же угол φ. Следовательно, в полярной системе координат второй координатой симметричной точки будет угол для исходной точки, взятый с противоположным знаком, то есть -φ. Итак, полярные координаты точки, симметричной данной относительно полярной оси будут отличаться лишь второй координатой, и эта координата будет с противоположным знаком. Полярные координаты искомых симметричных точек будут следующими:

Пример 2. В полярной системе координат на плоскости даны точки

Найти полярные координаты точек, симметричных этим точкам относительно полюса.

Решение. При симметрии длина луча не меняется. Следовательно, первая координата — длина луча — у симметричной относительно полюса точки будет как и у данной точки. Симметричная относительно полюса точка получается вращением исходной точки на 180 градусов против часовой стрелки, то есть на угол π. Следовательно, вторая координата точки, симметричной данной относительно полюса рассчитывается как φ + π (если в результате получится числитель больше знаменателя, то вычтем из полученного числа один полный оборот, то есть 2π). Получаем следующие координаты точек, симметричных данным относительно полюса:

Пример 3. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В полярной системе координат даны точки

Найти декартовы координаты этих точек.

Решение. Используем формулы перехода от полярных координат к декартовым:

Получаем следующие декартовы координаты данных точек:

Пример 4. Полюс полярной системы координат совпадает с началом декартовых прямоугольных координат, а полярная ось совпадает с положительной полуосью абсцисс. В декартовой прямоугольной системе координат даны точки

Найти полярные координаты этих точек.

Решение. Определяем первую из полярных координат по формуле , а тангенс угла φ — второй из полярных координат как . Получаем следующие полярные координаты данных точек:

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Полярная система координат (полярные координаты)

Полярная система координат на плоскости — это совокупность точки , называемой полюсом , и полупрямой , называемой полярной осью . Кроме того, задается масштабный отрезок для измерения расстояний от точек плоскости до полюса. Как правило, на полярной оси выбирается вектор , приложенный к точке , длина которого принимается за величину масштабного отрезка, а направление вектора задает положительное направление на полярной оси (рис.2.28,а).

Положение точки в полярной системе координат определяется расстоянием ( полярным радиусом ) от точки до полюса (т.е. ) и углом ( полярным углом ) между полярной осью и вектором . Полярный радиус и полярный угол составляют полярные координаты точки , что записывается в виде . Полярный угол измеряется в радианах и отсчитывается от полярной оси:

— в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;

— в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.

Полярный радиус определен для любой точки плоскости и принимает неотрицательные значения . Полярный угол определен для любой точки плоскости, за исключением полюса , и принимает значения , называемыми главными значениями полярного угла . В некоторых случаях целесообразно считать, что полярный угол определен с точностью до слагаемых , где . В этом случае значениям полярного угла для всех соответствует одно и то же направление радиус-вектора.

С полярной системой координат можно связать прямоугольную систему координат , начало которой совпадает с полюсом, а ось абсцисс (точнее положительная полуось абсцисс) — с полярной осью. Ось ординат достраивается перпендикулярно оси абсцисс так, чтобы получилась правая прямоугольная система координат (рис.2.28,б). Длины базисных векторов определяются масштабным отрезком на полярной оси.

Наоборот, если на плоскости задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим полярную систему координат <связанную с данной прямоугольной).

Выведем формулы, связывающие между собой прямоугольные координаты точки , отличной от точки , и ее полярные координаты . По рис.2.28,б получаем

Эти формулы позволяют найти прямоугольные координаты по известным полярным координатам. Обратный переход выполняется по формулам:

Последние два равенства определяют полярный угол с точностью до слагаемых , где . При из них следует, что . Главное значение полярного угла находится по формулам (рис.2.29):

Пример 2.9. В полярной системе координат :

а) изобразить координатные линии ;

б) изобразить точки с полярными координатами . Найти главные значения полярных углов этих точек;

в) найти прямоугольные координаты точек .

Решение. а) Координатные линии представляют собой окружности соответствующих радиусов, а линии и — полупрямые (рис.2.30,а).

б) Построим точки и (рис.2.30,б,в). Их координаты отличаются полярным углом, однако, имеют одно и то же главное значение . Следовательно, это одна и та же точка, которая совпадает с точкой , изображенной на рис.2.30,а.

в) Учитывая пункт «б», найдем прямоугольные координаты точки . По формулам (2.17) получаем:

1. Главное значение полярного угла можно выбрать иначе, например, .

2. Расстояние между двумя точками и (длина отрезка ) вычисляется по формуле

что следует из теоремы косинусов (рис.2.31).

3. Ориентированная площадь параллелограмма (рис.2.31), построенного на радиус-векторах и , находится по формуле

Она положительна, если (при этом ориентация пары радиус- векторов и правая), и отрицательна, если varphi_2″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAEcAAAASBAMAAAD73d5oAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMAwPxBoV0BgTEhELHR4JFxAbyQhgAAASJJREFUKM9jYCAdsEYRoyqmCqvwUgYGa1E4jy3mJczQCQzLRRZAOY8ZWBUPTUCoCvSEMGYzcJ0VcoCwOQUY1jZwFyAZbegBppwZ+Bw41CBC/AFALjuyIgZrCZCJxxgmMjBAFTFO4NrAwGLAwIlQNAWkiNkB6BCgNcYgZzE2sAYw9CSYX0cYJJwAVsQmwMAdsO7LDSCHbxt3A8dlhpniMIdDncSlwbGB7SHDbwZHEOdskalTAAMDTFEM1HMMnxyda6UYPjEUgThLlJRAeqGK4MHEwHpJ6T6I9gHzvNsY4IpYkQK8yQrkNg4NMEefAaEIGXwCqWFY2ADWrIxD0UGw+yVYQRS7Gg5FYBv4gq3B8QKONzvdSnRFBmA7lRQJJx22NKDLACxqN6Lf3w5xAAAAAElFTkSuQmCC» style=»vertical-align: middle;» /> (ориентация пары радиус-векторов и левая).

Пример 2.10. Даны полярные координаты и точек и (рис.2.32). Требуется найти:

а) скалярное произведение ;

б) длину отрезка ;

в) внешнее произведение ;

г) площадь треугольника ;

д) координаты середины отрезка в прямоугольной системе координат, связанной с данной полярной.

Решение. а) По определению скалярного произведения находим

б) Находим длину отрезка (см. пункт 2 замечаний 2.8):

в) Внешнее произведение находим как ориентированную площадь параллелограмма, построенного на векторах и :

Площадь положительная, так как векторы и образуют правую пару .

г) Площадь треугольника находим как половину площади параллелограмма, построенного на радиус-векторах и .

д) По формулам (2.17) находим прямоугольные координаты точек и :

а затем координаты середины отрезка (см. пункт 3 замечаний 2.1):

Пример 2.11. На координатной плоскости отмечена точка . Найти:

а) полярные координаты точки , образа точки при повороте радиус-вектора на угол вокруг начала координат (рис.2.33);

б) полярные координаты точки , образа точки при инверсии плоскости относительно окружности единичного радиуса с центром в начале координат (см. пример б преобразований плоскости в разд. 2.2.4).

Решение. а) Найдем полярные координаты точки . По формулам (2.17), учитывая рис.2.29, получаем:

так как точка лежит в четверти.

При повороте радиус-вектора вокруг полюса на угол полярный радиус не изменяется, а полярный угол увеличивается. Следовательно, полярные координаты точки : , , причем — главное значение полярного угла .

б) При инверсии относительно окружности радиуса полярные координаты образа выражаются через полярные координаты прообраза следующими формулами:

Поэтому, учитывая пункт «а», находим (для ):