Часто в задачах источников магнитного поля несколько. Тогда возникает вопрос о суммарном векторе магнитной индукции в интересующей нами точке пространства. В общем, принцип суперпозиции звучит как: суммарный вектор магнитной индукции в точке есть векторная сумма векторов магнитной индукции от каждого из источников или формульно:
- где
- — вектор полной магнитной индукции в точке,
- — векторная сумма векторов магнитной индукции от каждого из источников.
Рис. 1. Принцип суперпозиции магнитных полей
Пусть даны два магнитных поля, индукция которых в некой точке А равны и (рис. 1.1). Полный вектор магнитной индукции суммарного поля найдём из (1) как: . Нахождение суммарного вектора — вопрос математического сложения векторов. Воспользуемся правилом параллелограмма для нахождения суммарного вектора (рис. 1.2). Для нахождения модуля этого вектора чаще всего пользуются или теоремой Пифагора, или теоремами синусов/косинусов. В случае нескольких источников магнитного поля (несколько векторов), для получения общего вектора необходимо их всех векторно сложить (к сожалению, это иногда трудновато, но можно).
Принцип суперпозиции магнитных полей
теория по физике 🧲 магнетизм
Если в некоторой точке пространства накладываются магнитные поля, то результирующий вектор магнитной индукции находят как геометрическую сумму вектором магнитной индукции, составляющих магнитное поле:
Частные случаи принципа суперпозиции полей
| Сложение векторов магнитной индукции, направленных вдоль одной прямой | |
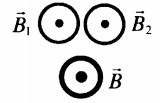 | Если → B 1 ↑ ⏐ ⏐ ↑ ⏐ ⏐ → B 2 , то: |
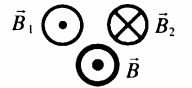
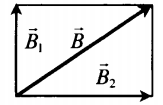
B = √ B 1 2 + B 2 2
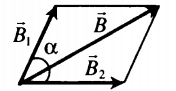
B = √ B 1 2 + B 2 2 − 2 B 1 B 2 cos . ( 180 ° − α )
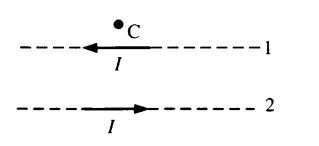
Пример №1. По двум тонким прямым проводникам, параллельным друг другу, текут одинаковые токи I (см. рисунок). Как направлено (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) создаваемое ими магнитное поле в точке С?
Чтобы определить направление результирующего вектора магнитной индукции, сначала определим направление линий магнитной индукции в точке С для каждого из полей. Применив правило буравчика, получим, что силовые линии первого поля направлены в точке С от нас, а второго поля — к нам. Но точка С находится на разных расстояниях от проводников. Она ближе к проводнику 1. Поскольку магнитное поле ослабевает с увеличением расстояния, то модуль вектора магнитной индукции первого поля в точке С будет больше вектора магнитной индукции второго поля. Поскольку они не компенсируют друг друга, и первое поле в этой точке сильнее второго, то результирующий вектор магнитной индукции в точке С направлен в сторону от наблюдателя.
На рисунке показаны сечения двух параллельных прямых длинных проводников и направления токов в них. Сила тока в проводниках одинакова. Куда направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор индукции созданного проводниками магнитного поля в точке А, расположенной на равном расстоянии от проводников? Ответ запишите словом (словами).
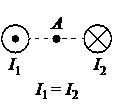
Алгоритм решения
Решение
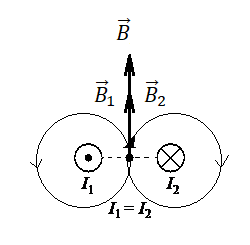
Направление вектора магнитной индукции в точке А для обоих проводников можно определить с помощью правила буравчика. Мысленно направим буравчик по направлению тока в первом проводнике. Тогда получим, что силовые линии магнитного поля направлены против хода часовой стрелки. Поэтому вектор → B 1 магнитной индукции в точке А направлен относительно рисунка вверх.
Поскольку во втором проводнике направление тока противоположно направлено току в первом проводнике, силовые линии создаваемого им магнитного поля направлены по ходу часовой стрелки. Но так как точка А относительно этого проводника расположена не справа, а слева, то вектор → B 2 магнитной индукции в ней тоже направлен вверх.
Поскольку сила тока в обоих проводниках одинаковая, результирующий вектор магнитной индукции в точке А равен удвоенному вектору магнитной индукции поля, создаваемого каждым из этих проводников. В этом случае он направлен вверх так же как векторы → B 1 и → B 2 .
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показаны сечения двух параллельных длинных прямых проводников и направления токов в них. Сила тока I1 в первом проводнике больше силы тока I2 во втором. Куда направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор индукции магнитного поля этих проводников в точке А, расположенной точно посередине между проводниками? Ответ запишите словом (словами).
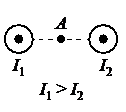
Алгоритм решения
Решение
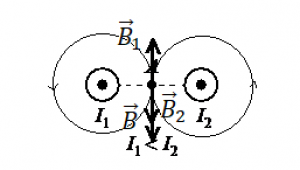
Направление вектора магнитной индукции в точке А для обоих проводников можно определить с помощью правила буравчика. Мысленно направим буравчик по направлению тока в первом проводнике. Тогда получим, что силовые линии магнитного поля направлены против хода часовой стрелки. Поэтому вектор → B 1 магнитной индукции в точке А направлен относительно рисунка вверх.
Поскольку во втором проводнике направление тока совпадает с направлением тока в первом проводнике, силовые линии создаваемого им магнитного поля тоже направлены против хода часовой стрелки. Но так как точка А относительно этого проводника расположена не справа, а слева, то вектор → B 2 магнитной индукции в ней направлен вниз.
Поскольку сила тока в первом проводнике больше, он создает более сильное магнитное поле. Следовательно, модуль вектора → B 1 магнитной индукции больше модуля вектора → B 2 . Тогда вектор, являющийся их геометрической суммой, будет направлен вверх.
pазбирался: Алиса Никитина | обсудить разбор | оценить
На рисунке показаны сечения двух параллельных длинных прямых проводников и направления токов в них. Как направлен относительно рисунка (вправо, влево, вверх, вниз, к наблюдателю, от наблюдателя) вектор магнитной индукции в точке А, находящейся точно посередине между проводниками, если сила тока I2 во втором проводнике больше силы тока I1 в первом проводнике? Ответ запишите словом (словами).
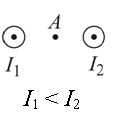
Алгоритм решения
Решение
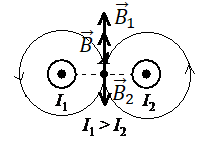
Направление вектора магнитной индукции в точке А для обоих проводников можно определить с помощью правила буравчика. Мысленно направим буравчик по направлению тока в первом проводнике. Тогда получим, что силовые линии магнитного поля направлены против хода часовой стрелки. Поэтому вектор → B 1 магнитной индукции в точке А направлен относительно рисунка вверх.
Поскольку во втором проводнике направление тока совпадает с направлением тока в первом проводнике, силовые линии создаваемого им магнитного поля тоже направлены против хода часов стрелки. Но так как точка А относительно этого проводника расположена не справа, а слева, то вектор → B 2 магнитной индукции в ней направлен вниз.
Поскольку сила тока во втором проводнике больше, он создает более сильное магнитное поле. Следовательно, модуль вектора → B 2 магнитной индукции больше модуля вектора → B 1 . Тогда вектор, являющийся их геометрической суммой, будет направлен вниз.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Сложение векторов магнитной индукции
где μ0 = 4p·10 -7 Гн/м — магнитная постоянная.
Формула (3.6.1) записана в системе СИ. Это соотношение было установлено в 1820 г. Андре Ампером и носит название закона Ампера.
С помощью формулы (3.6.1) устанавливается единица силы тока в системе СИ: 1 А определяется как сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м в вакууме, вызвал бы между этими проводниками силу, равную 2·10 -7 Н на каждый метр длины.
Взаимодействие токов осуществляется посредством поля, которое называется магнитным . Для исследований магнитного поля применяют пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров. Ориентацию контура в пространстве характеризует вектор нормали к его плоскости, причем положительным считают направление нормали, связанное с направлением тока по правилу правого винта (Рис. 3.6.1).
Рис. 3.6.1. Пробный контур
Если внести пробный контур в магнитное поле, то обнаружится, что поле оказывает на контур ориентирующее действие, поворачивая его в определенном направлении. Это направление и принимают за направление магнитного поля в данной точке. Если контур повернуть так, чтобы направления нормали и поля не совпадали, возникает вращающий момент, стремящийся вернуть контур в равновесное положение. Величина этого момента зависит от угла a между нормалью и направлением тока, достигая наибольшего значения Ммакс при α=90°, и обращается в нуль при α=0°.
Введем магнитный момент контура:
| (3.6.2) |
где S — площадь контура.
Тогда, исходя из опыта, можно записать:
| (3.6.3) |
где для количественной характеристики магнитного поля введена физическая величина, называемая магнитной индукцией .
Соотношение (3.6.3) определяет модуль вектора В. Следовательно, выполняется:
| (3.6.4) |
Направление вектора совпадает с направлением нормали к пробному контуру. Поле этого вектора наглядно представляют с помощью линий магнитной индукции.
Из сказанного следует, что вектор характеризует силовое действие магнитного поля.
3.6.2. Закон Био-Савара-Лапласа.
Магнитные поля прямого и кругового токов
Для расчета магнитной индукции поля в результате обобщения экспериментальных данных Био и Савара Лаплас предложил формулу:
| (3.6.5) |
где i — сила тока, — вектор, совпадающий с элементарным участком тока и направленный так же, как и ток, — вектор, проведенный от элемента тока в ту точку, где производится наблюдение поля (Рис. 3.6.2).
Рис. 3.6.2. К закону Био-Савара-Лапласа
Направление вектора задается векторным произведением в (3.6.5), т.е. этот вектор направлен перпендикулярно плоскости, в которой лежат вектора и , причем так, что, если смотреть из конца вектора , то поворот от вектора к производится против часовой стрелки. Единицей магнитной индукции в СИ является 1 Тл (Тесла).
Модуль вектора можно вычислить с помощью формулы:
| (3.6.6) |
где α — угол между векторами и .
Рассмотрим поле, создаваемое током, текущим по бесконечному прямому проводу (Рис. 3.6.3).
Рис. 3.6.3. К расчету магнитного поля бесконечного прямого проводника
Все векторы в данной точке имеют одинаковое направление (перпендикулярно плоскости чертежа и за него).
Поэтому сложение этих векторов можно заменить сложением их модулей. Пусть точка, для которой вычисляется поле, находится на расстоянии b от проводника. Из Рис. 3.6.3 ясно, что:
| (3.6.7) |
Подставим этот результат в формулу (3.6.6):
| (3.6.8) |
Угол α изменяется от 0 до π. Следовательно, получим:
| (3.6.9) |
Линии магнитной индукции поля прямого проводника представляют собой систему концентрических окружностей (Рис. 3.6.4).
Рис. 3.6.4. Магнитное поле прямого проводника
Рассмотрим поле, создаваемое током, текущим по проводнику в виде окружности радиуса R (Рис. 3.6.5).
Рис. 3.6.5. К расчету поля кругового тока
Найдем магнитную индукцию в центре окружности. Каждый элемент тока создает в центре индукцию, направленную вдоль положительной нормали к контуру. Ее направление определяется по правилу правого винта. Поэтому вычисление магнитной индукции сводится к сложению модулей. Поскольку α = π/2, то из формулы (3.6.6) следует:
| (3.6.10) |
Интегрируя (3.6.10) по всему контуру, получим:
| (3.6.11) |
Найдем магнитную индукцию на оси кругового тока, на расстоянии х от плоскости, в которой лежит контур (Рис. 3.6.6).
Рис. 3.6.6. Магнитное поле на оси кругового тока
Векторы перпендикулярны к плоскостям, проходящим через векторы и . Следовательно, они образуют симметричный конус. Ясно, что результирующий вектор должен быть направлен по оси контура. Каждый из векторов вносит вклад , который по модулю равен:
| (3.6.12) |
Угол между векторами и — прямой, поэтому выполняется:
| (3.6.13) |
Интегрируя по всему контуру с током и учитывая, что , получим:
| (3.6.14) |
При х = 0 эта формула переходит в (3.6.11) для индукции магнитного поля в центре кругового тока.
3.6.3. Магнитное поле в веществе
Если несущие ток проводники находятся в какой-либо среде, магнитное поле заметно изменится. Это объясняется тем, что любое вещество является магнетиком, т.е. способно под действием магнитного поля приобретать магнитный момент (намагничиваться). Намагниченное вещество создает магнитное поле ´, которое складывается с полем, обусловленным токами 0. Оба поля в сумме дают результирующее усредненное (макроскопическое) поле в среде:
| (3.6.15) |
Для объяснения явления намагничивания тел Ампер предположил, что в атомах вещества циркулируют круговые токи. Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего поля молекулярные токи ориентированы беспорядочным образом, вследствие чего их результирующее магнитное поле равно нулю. Под действием поля магнитные моменты атомов приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается. — его суммарный магнитный момент становится отличным от нуля. Возникает поле ´.
Намагниченность вещества характеризуют магнитным моментом единицы объема. Эту величину называют вектором намагниченности . В общем случае имеем:
| (3.6.16) |
где ΔV — физически бесконечно малый объем, взятый в окрестности рассматриваемой точки, — магнитный момент отдельной молекулы.
Суммирование производится по всем молекулам, заключенным в объеме ΔV.
Найдем поток вектора через произвольную замкнутую поверхность:
| (3.6.17) |
Опыт показывает, что линии магнитного поля, в отличие от линий напряженности электрического поля, всегда замкнуты. Поэтому интеграл в (3.6.17) должен быть равен нулю, поскольку каждая из линий магнитной индукции пересекает замкнутую поверхность четное число раз — входит в поверхность столько же раз, сколько и выходит. Следовательно, выполняется:
| (3.6.18) |
Это равенство выражает теорему Гаусса для вектора магнитной индукции: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю .
Для описания магнитных свойств магнетиков удобно использовать вспомогательную величину — напряженность магнитного поля :
| (3.6.19) |
Единица измерения в СИ — 1 А/м. Величина напряженности магнитного поля зависит только от суммы макроскопических токов и не зависит от молекулярных токов. В свою очередь, намагниченность зависит только от суммы молекулярных токов. Как показывает опыт, намагниченность пропорциональна величине напряженности магнитного поля:
| (3.6.20) |
где χ — материальная характеристика способности тел намагничиваться, называемая магнитной восприимчивостью .
Подставляя (3.6.20) в (3.6.19), получим:
| (3.6.21) |
где μ = 1 + χ — магнитная проницаемость вещества.
Из (3.6.21) получается простое соотношение:
| (3.6.22) |
которое называют материальным уравнением магнитостатики.
Для вакуума χ = 0, μ = 1, и уравнение (3.6.22) будет иметь вид:
| (3.6.23) |
Как в уравнении (3.6.22), так и в уравнении (3.6.23) поле имеет смысл внешнего магнитного поля. Перепишем (3.6.19) в виде:
| (3.6.24) |
Сравнивая (3.6.24) с (3.6.15), с учетом (3.6.23) имеем:
| (3.6.25) |
Подставляя (3.6.23) в (3.6.21), имеем:
| (3.6.26) |
Отсюда следует важный вывод: относительная магнитная проницаемость показывает, во сколько раз усиливается магнитное поле в магнетике по сравнению с вакуумом.
© ФГОУ ВПО Красноярский государственный аграрный университет, 2015