Сколько окружностей можно провести через три точки

Через три точки А, В и С , не лежащие на одной прямой (через вершины >>

Сколько окружностей можно провести через 3 точки, не лежащие на одной прямой? Через три точки, не лежащие на одной прямой, можно провести окружность и притом только одну. Доказательство.

Слайд 20 из презентации «Окружность»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Окружность.ppt» можно в zip-архиве размером 557 КБ.

Окружность

«Построение касательной к окружности» — Решение. Касательная к окружности. Хорда. Взаимное расположение прямой и окружности. Окружность и прямая имеют одну общую точку. Окружность. Окружность и прямая. Теорема об отрезках касательных. Общие точки. Повторение. Диаметр.

«Длина окружности 6 класс» — Сейчас волшебный дворец находится под охраной ЮНЕСКО. История числа ?. Творческих успехов! Длина окружности. Актуализация знаний. На готовых моделях окружностей определить длины окружности и диаметра с помощью нити. Диаметр земного шара приближенно равен 12,7 тыс. км. 23. Конкурс «Мозаика презентаций».

«Окружность 7 класс» — Отрезок, соединяющий две точки окружности, называется ее хордой. Построения циркулем и линейкой. Вводная беседа «В мире окружностей». Цели урока. Провести окружность произвольного радиуса. По готовым рисункам определить радиусы, хорды, диаметры, дуги. Окружность произвольного радиуса. У круга есть одна подруга.

«Окружность и круг геометрия» — Окружность. А знаешь ли ты: Длина окружности. L=2?R. Историческая справка. Площадь круга. Окружность и круг. Фигура, ограниченная окружностью, называется кругом. Круг.

«Окружность и круг урок» — Заключение. Изучение нового материала Закрепление изученного материала Подведение итогов урока. Дополнительные задачи. План урока: Вступительное слово учителя, объявление темы и цели урока. Задачи. Математика. Найдите радиус окружности, проходящей через центры данных окружностей. Содержание. Тест для подготовки к ЕГЭ.

«Окружность и круг» — Точку называют центром окружности. Круг. Дуга. Категория — высшая. Любимое занятие-чтение. МАТЕМАТИКА-5 Тематическое планирование Ход урока Автор Ресурсы. Тренировочные упражнения. Часть окружности называется дугой.

Сколько окружностей можно провести через три точки

Какие из следующих утверждений верны?

1) Через любые три точки проходит не более одной окружности.

2) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.

3) Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются.

4) Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

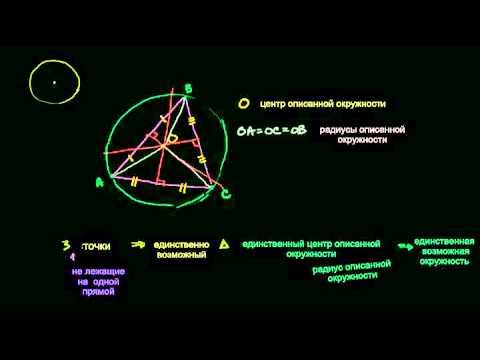
1) «Через любые три точки проходит не более одной окружности.» — верно, Через любые три точки, не лежащие на одной прямой, проходит единственная окружность. Если точки лежат на одной прямой, то окружность провести невозможно. Тем самым, через любые три точки можно провести не более одной окружности.

2) «Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти окружности не имеют общих точек.» — верно, если расстояние от центра до прямой меньше радиуса, то окружности имеют две общие точки, если окружности касаются то окружности имеют одну общую точку, если расстояние больше радиуса, то окружности не имеют общих точек.

3) «Если радиусы двух окружностей равны 3 и 5, а расстояние между их центрами равно 1, то эти окружности пересекаются» — неверно, окружность, радиус которой равен 3, лежит внутри окружности с радиусом 5.

4) «Если дуга окружности составляет 80°, то вписанный угол, опирающийся на эту дугу окружности, равен 40°.» — верно, вписанный угол измеряется половиной дуги,на которую он опирается.

Сколько окружностей можно провести через три точки

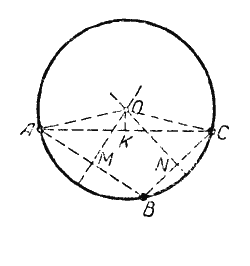
Пусть нам даны три точки А, В и С, не лежащие на одной прямой (см. рис.).

Соединим эти точки отрезками АВ и ВС. Чтобы найти точки равноудалённые от точек А и В разделим отрезок АВ пополам и через середину (точку М) проведём прямую перпендикулярную к АВ. Каждая точка этого перпендикуляра одинаково удалена от точек А и В.

Чтобы найти точки, равноудалённые от точек В и С, разделим отрезок ВС пополам и через его середину (точку N) проведемпрямую, перпендикулярную ВС. Каждая точка этого перпендикуляа одинаково удалена от точек В и С.

Точка О пересечения этих перпендикуляров будет находиться на одинаковом расстоянии от данных точек А, В и С (АО = ВО = СО). Если мы, приняв точку О за центр круга, радиусом, равным АО, проведём окружность, то она пройдёт через все данные точки А, В и С.

Точка О является единственной точкой, которая может служить центром окружности, проходящей через три точки А, В и С, не лежащие на одной прямой, так как два перпендикуляра к отрезкам АВ и ВС могут пересечься только в одной точке. Значит, задача имеет единственное решение.

Примечание. Если три точки А, В и С будут лежать на одной прямой, то задача не будет иметь решения, так как перпендикуляры к отрезкам АВ и ВС будут параллельны и не будет существовать точки, одинаково удаленной от точек А, В, С, т. е. точки, которая могла бы служить центром искомой окружности.

Если соединить отрезком точки А и С и середину этого отрезка (точку К) соединить с центром окружности О, то ОК будет перпендикулярна к АС (рис.), так как в равнобедренном треугольнике АОС ОК является медианой, поэтому ОК ⊥ АС.

Следствие. Три перпендикуляра к сторонам треугольника, проведённые через их середины пересекаются в одной точке.

📹 Видео