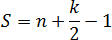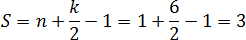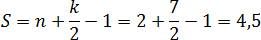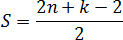Сколько других узлов сетки лежат на этой окружности (8 видео)

Глава 3. Сколько узлов на отрезке?

Применение формулы Пика для вычисления площадей некоторых фигур не совсем удобно. Очень уж чётким должен быть чертёж и очень внимательно нужно его рассматривать, чтобы определить, лежит ли данный узел внутри фигуры или же попал на её границу. Как точно сосчитать число узлов на границе? Поскольку граница состоит из отрезков, то нас интересует количество узлов сетки, лежащих на произвольном отрезке с концами в узлах.

Сделаем сначала небольшое наблюдение. Пусть А и В – узлы сетки. Обозначим через С первый узел, встречавшиеся после А на отрезке АВ (значит, между А и С больше нет узлов). Построим прямоугольный треугольник А С D с гипотенузой А С и катетами, лежащими на линиях сетки (рис.1).

Если С ≠ В, то сместим этот треугольник вдоль

отрезка АВ на расстояние А С . Получим равный

ему треугольник С С D .

Следовательно, С – узел, и между С и С нет узлов. Ясно,

что если эту процедуру продолжить, мы когда-нибудь

получим в качестве очередной точки С точку В – узел

сетки. Рассматривая большой прямоугольный треугольник

ARB с гипотенузой АВ, приходим к равенствам: Рис. 1

AR = (k+1) · AD ,

BR = (k+1) · С D , (1)

AB = (k+1) · A С ‌

Теперь мы можем выяснить, сколько узлов Рис. 2. лежит между точками А и В(конечно, мы считаем, что А и В не лежат на одной линии сетки). Построим прямоугольный треугольник ARB с вершинами в узлах сетки и с гипотенузой АВ (рис.2).

Пусть AR = р, BR = q. Понятно, что р и q – целые положительные числа.

Теорема. Если р и q взаимно просты, то между А и В на отрезке АВ нет узлов сетки. Если же наибольший общий делитель р и q равен n , где n > 1 (НОД (р, q ) = n > 1), то на отрезке АВ между точками А и В расположены ровно ( n – 1) узлов сетки.

Доказательство. 1) Пусть числа p и q взаимно просты. Если между А и В были k узлов (k ≥ 1), то, взяв ближайший к А узел С , мы получим по формулам (1): p =(k+1) · AD , q = (k +1) · С D , то есть р и q имеют общий делитель k + 1, больший 1. Но ведь они взаимно просты!

2)Пусть НОД (р,q) = n > 1. Поделив отрезки AR и BR на n равных частей, мы опять приходим к рис.1, где С , С , …, С – какие-то узлы сетки и k=n – 1. Таким образом, в этом случае между точками А и В есть хотя бы n – 1 узел. Почему их не может быть больше, чем n – 1? В этом случае между узлами А и С были бы и другие узлы. Пусть С¢ – ближайший к А узел. Тогда АС´

Сколько клеток рассекает на две части диагональ прямоугольника m×n, где m и n – взаимно простые числа?

Заметим, что диагональ такого прямоугольника не проходит через узлы. Будем считать, что диагональ идёт из левого нижнего угла прямоугольника. Самой первой она рассекает левую нижнюю угловую клетку (клетку № 1), потом она попадёт в клетку № 2 (рис.4), и так далее. Пусть диагональ уже пересекла k клеток. Так как она ни разу не проходит через узел, то всегда можно однозначно указать, какую клетку она рассечёт после клетки с номером k.

Итак, мы получили «цепочку», идущую из левого нижнего угла в правый верхний. Нам надо понять,

Рис. 4 чему равно число клеток в этой цепочке. Дадим каждой клетке адрес (t, s), если она расположена в горизонтальном ряду с номером t и вертикальном ряду с номером s. Левый нижний угол получает адрес (1,1), а правый верхний – (m,n). Теперь остаётся заметить, что при переходе от клетки с номером k в нашей цепочке к клетке с номером k+1 сумма чисел t и s в адресе возрастает точно на 1. Значит,

чтобы перейти от клетки с адресом (1,1) к клетке с адресом (m,n), надо сделать ровно m + n – 2 шагов, пройдя, таким образом, m + n – 1 клеток.

Итак, ответ к задаче 3 – число клеток равно 2002.

Объединим задачи 2 и 3.

Пусть m и n – произвольные натуральные числа.

Сколько клеток рассекает диагональ

Пусть d = НОД (m×n). Как и при решении задачи 2,

мы видим, что вдоль диагонали исходного

прямоугольника образуется d маленьких прямоугольников ´ . Стороны этих маленьких прямоугольников уже взаимно просты, поэтому их диагонали рассекают по + – 1 клеток каждая. Значит, диагональ исходного прямоугольника рассечёт ( + – 1) · d = m + n – d клеток.

Теперь при желании мы можем без труда сосчитать, сколько клеток рассекут диагонали следующих прямоугольников: 36×56, 105×24, 2003×111.

Заключение

Предметом исследования явилось применение формулы Пика при решении задач, на нахождение площади фигур, изображённых на клетчатой бумаге.

При выполнении работы были решены задачи на нахождение площади многоугольников, изображённых на клетчатой бумаге различными способами: непосредственного применения формул, геометрическим и с помощью формулы Пика. Анализ решений показал, что применение формулы Пика даёт возможность решать задачи на нахождение площади многоугольника, изображённого на клетчатой бумаге быстро и легко. Это позволяет экономить время на ЕГЭ по математике.

Эта работа вызвала у нас интерес, и мы надеемся, что наши выводы, полученные в результате наших исследований, помогут выпускникам одиннадцатых классов при сдаче ЕГЭ по математике.В результате нашей работы мы расширили свои знания о решении задач на клетчатой бумаге, определили для себя классификацию исследуемых задач, убедились в их многообразии.

Мы научились вычислять площади многоугольников, нарисованных на клетчатом листке, встретились с совсем новыми, необычными «расстояниями», узнали, как раскраска клеточек помогает решать многие задачи.

Рассмотренные нами задания имеют различный уровень трудности – от простых до олимпиадных. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных.

Работа по данной теме позволила нам преодолеть психологический барьер и поверить в свои силы, что является важнейшим фактором успешного решения олимпиадных и экзаменационных задач, выступления перед аудиторией с теоретическим материалом по математике.

Мы пришли к выводу, что тема, которая нас заинтересовала, достаточно многогранна, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны.

Список используемой литературы

1. Болотин И. Б., Добрышина Л. Ф. Смоленские математические олимпиады школьников (готовимся к ЕГЭ). Смол. гос. ун-т; Смоленск: СмолГУ, 2008.

2.Васильев Н.Б. Вокруг формулы Пика, журнал «Квант» №12,1974 г., с.39-43.

3. Геометрия на клетчатой бумаге. Малый МЕХмат МГУ. Режим доступа: http://mmmf.msu.ru/archive/20082009/KanunnikovKuznetsov/2.html

4. Григорьева Г. И . Подготовка школьников к олимпиадам по математике: 5 – 6 классы. Метод. пособие. – М.: Глобус, 2009.

5. Дынкин Е. Б., Молчанов С. А., Розенталь А. Л . Математические соревнования. Арифметика и алгебра. – М.: Наука, 1970.

6. Жарковская Н. М., Рисс Е. А . Геометрия клетчатой бумаги. Формула Пика // Математика, 2009, № 17, с. 24-25

7. Задачи открытого банка заданий по математике ФИПИ, 2010 – 2011. Режим доступа: http://mathege.ru/or/ege/ShowProblems.html?posMask=32

8. Игнатьев Е. И . В царстве смекалки. – М.: Наука, 1982.9. Кенгуру – 2010. Задачи, решения, итоги. Режим доступа: http://russian-kenguru.ru/load

9. Прасолов В. В . Задачи по планиметрии. – М.: МЦНМО, 2000.

11. Рисс Е. А . Математический клуб «Кенгуру» Выпуск № 8 (изд. второе). – Санкт-Петербург, 2009.

12. Смирнова И. М., Смирнов В. А . Геометрия на клетчатой бумаге. – М.: Чистые пруды, 2009.

13. Смирнова И. М., Смирнов В. А . Геометрические задачи с практическим содержанием. – М.: Чистые пруды, 2010.

14. Смирнов В. А. ЕГЭ. Математика. Задача В6. Планиметрия. Р/т. – М.: МЦНМО, 2011.

15. Трошин В. В. Занимательные дидактические материалы по математике. Сборник заданий. Выпуск 2. – М.: Глобус, 2008.

16. Гарднер М. Математические чудеса и тайны. – М.: Наука, 1986.

Содержание

Метод узлов в задаче B5
Важное замечание по площадям
Окружности на клетчатой бумаге
Задача
Подсказка 1
Подсказка 2
Подсказка 3
Решение
Послесловие
🌟 Видео

Видео:№8. Верно ли утверждение: а) если две точки окружности лежат в плоскостиСкачать

Метод узлов в задаче B5

Существует замечательная формула, которая позволяет считать площадь многоугольника на координатной сетке почти без ошибок. Это даже не формула, а настоящая теорема. На первый взгляд, она может показаться сложной. Но достаточно решить пару задач — и вы поймете, насколько это крутая фишка. Так что вперед!

Для начала введем новое определение:

— это любая точка, лежащая на пересечении вертикальных и горизонтальных линий этой сетки.

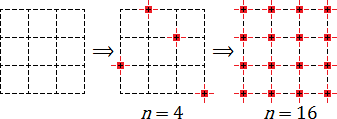
На первой картинке узлы вообще не обозначены. На второй обозначены 4 узла. Наконец, на третьей картинке обозначены все 16 узлов.

Какое отношение это имеет к задаче B5? Дело в том, что вершины многоугольника в таких задачах всегда лежат в узлах сетки. Как следствие, для них работает следующая теорема:

Теорема. Рассмотрим многоугольник на координатной сетке, вершины которого лежат в узлах этой сетки. Тогда площадь многоугольника равна:

где n — число узлов внутри данного многоугольника, число узлов, которые лежат на его границе (граничных узлов).

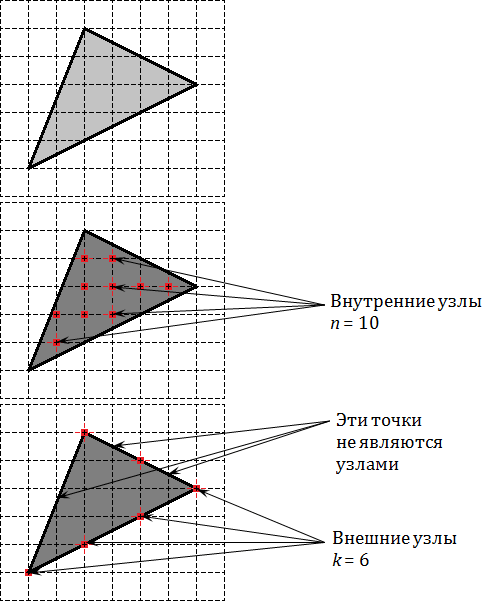
В качестве примера рассмотрим обычный треугольник на координатной сетке и попробуем отметить внутренние и граничные узлы.

На первой картинке дан обычный треугольник. На второй отмечены его внутренние узлы, число которых равно На третей картинке отмечены узлы лежащие на границе, их всего

Возможно, многим читателям непонятно, как считать числа Начните с внутренних узлов. Тут все очевидно: закрашиваем треугольник карандашом и смотрим, сколько узлов попало под закраску.

С граничными узлами чуть сложнее. Граница многоугольника — замкнутая ломаная, которая пересекает координатную сетку во многих точках. Проще всего отметить какую-нибудь «стартовую» точку, а затем обойти остальные.

Граничными узлами будут только те точки на ломаной, в которых одновременно пересекаются

Собственно, ломаная;
Горизонтальная линия координатной сетки;
Вертикальная линия.

Посмотрим, как все это работает в настоящих задачах.

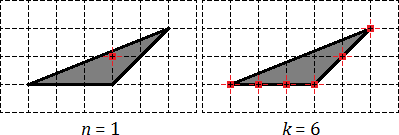
Задача. Найдите площадь треугольника, если размер клетки равен 1 x 1 см:

Для начала отметим узлы, которые лежат внутри треугольника, а также на его границе:

Получается, что внутренний узел всего один: Граничных узлов — целых шесть: три совпадают с вершинами треугольника, а еще три лежат на сторонах.

Теперь считаем площадь по формуле:

Вот и все! Задача решена.

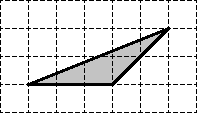
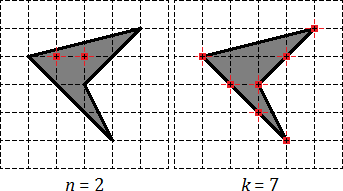
Задача. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см на 1 см. Ответ дайте в квадратных сантиметрах.

Снова отмечаем внутренние и граничные узлы. Внутренних узлов всего Граничных узлов: из которых 4 являются вершинами четырехугольника, а еще 3 лежат на сторонах.

Остается подставить числа в формулу площади:

Обратите внимание на последний пример. Эту задачу реально предлагали на диагностической работе в 2012 году. Если работать по стандартной схеме, придется делать много дополнительных построений. А методом узлов все решается практически устно.

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Важное замечание по площадям

Но формула — это еще не все. Давайте немного перепишем формулу, приведя слагаемые в правой части к общему знаменателю. Получим:

Числа n и k — это количество узлов, они всегда целые. Значит, весь числитель тоже целый. Мы делим его на 2, из чего следует важный факт:

Площадь всегда выражается целым числом или дробью. Причем в конце дроби всегда стоит «пять десятых»: 10,5; 17,5 и т.д.

Таким образом, площадь в задаче B5 всегда выражается целым числом или дробью Если ответ получается другим, значит, где-то допущена ошибка. Помните об этом, когда будете сдавать настоящий ЕГЭ по математике!

Видео:Окружности №1 в ЕГЭ | Профильная математика ЕГЭ 2024 | УмскулСкачать

Окружности на клетчатой бумаге

Видео:A и B сидели на трубе... | Что такое окружность Аполлония?Скачать

Задача

а) Постройте окружность, проходящую ровно через 12 узлов клетчатой бумаги.
б) Постройте окружность, проходящую ровно через 6 узлов клетчатой бумаги.
в) Постройте окружность, проходящую ровно через 5 узлов клетчатой бумаги.

Видео:МАТЕМАТИК ФУФАЕВ: Перельман, Казино, Мультивселенная, Золотое сечениеСкачать

Подсказка 1

Обратите внимание, что если центр окружности сам является узлом клетчатой бумаги, то количество лежащих на этой окружности узлов кратно четырём. Если же центр окружности находится в середине стороны какой-либо клеточки, то на такой окружности будет расположено чётное число узлов. Это относится и к тем случаям, когда окружность вообще не проходит через узлы клетчатой бумаги, потому что ноль делится как на 2, так и на 4 (и вообще на любое натуральное число).

Видео:Определение центра дуги окружности, построение окружности по 3 точкамСкачать

Подсказка 2

Будем считать, что расстояние между соседними узлами клетчатой бумаги равно единице. Тогда на ней можно задать систему координат таким образом, чтобы множество всех узлов в точности совпадало со множеством всех точек, обе координаты которых целочисленны.

а) Воспользуйтесь тем фактом, что если центр окружности радиуса r является началом координат, то количество лежащих на ней узлов клетчатой бумаги есть число целочисленных решений уравнения

б) Если r 2 — нечётное целое число, то в каждой паре вида (x, y), являющейся решением уравнения (1), одно из чисел чётное, а другое — нечётное, причём количество пар, в которых первое число нечётное, равно количеству пар, в которых второе число нечётное.

в) В качестве центра такой окружности можно выбрать точку (1/3, 0).

Видео:ЕГЭ-2020. №16. Вневписанная окружность🚀 Ортоцентр. Теорема Карно, Бланшета, Чевы, Менелая🔥Скачать

Подсказка 3

Попробуйте изучить окружности, квадраты радиусов которых имеют вид 5 k , 5 k /4 и 5 k /9 соответственно.

Видео:Все о вписанных и описанных окружностях с нуля | PARTAСкачать

Решение

а) Рассмотрим уравнение

Его решениями являются двенадцать пар чисел вида (±5, 0), (0, ±5), (±3, ±4) и (±4, ±3). Нетрудно убедиться простым перебором, что других целочисленных решений данное уравнение не имеет. Следовательно, на окружности радиуса 5 с центром в начале координат лежит ровно 12 узлов клетчатой бумаги (рис. 1).

б) Пусть центр окружности радиуса 5/2 расположен в точке (1/2, 0). Тогда эта окружность задаётся уравнением

Домножая обе части равенства на 4, можно перейти к такому соотношению:

Если же сделать переобозначения вида a = (2x – 1) и b = 2y, то мы придём к уравнению вида a 2 + b 2 = 25. Оно, как мы знаем из пункта а), имеет в точности 12 целочисленных решений (потому что это решения уравнения (2)), причём ровно в половине из них число a нечётное, а число b — чётное. Значит, уравнение (3) обладает в точности шестью целочисленными решениями. А именно, ему удовлетворяют следующие пары чисел: (3, 0), (–2, 0), (2, ±2) и (–1, ±2). Таким образом, на окружности радиуса 5/2 с центром в точке (1/2, 0) лежит ровно 6 узлов клетчатой бумаги (рис. 2).

в) Внимательный читатель наверняка заметил, что решение пункта б), по существу, вытекало из пункта а). Более того, можно было рассмотреть задачу в более общем виде и доказать такое утверждение: если на окружности радиуса r, центр которой находится в начале координат, лежит 4n узлов клетчатой бумаги и число r 2 — нечётное, то на окружности радиуса r/2 с центром в точке (1/2, 0) расположено 2n узлов. Ниже на примере нашей задачи мы покажем, как подобным методом получить окружность, на которой лежит ровно n узлов.

Для начала рассмотрим окружность с центром в начале координат, радиус которой равен 25. Эта окружность задаётся уравнением

которому, как нетрудно проверить, удовлетворяют двадцать пар целочисленных решений: (±25, 0), (0, ±25), (±7, ±24), (±24, ±7), (±15, ±20) и (±20, ±15). То есть на этой окружности находится ровно 20 узлов клетчатой бумаги.

Теперь рассмотрим окружность радиуса 25/3, центром которой является точка (1/3, 0). Задающее её уравнение имеет вид

что после соответствующих преобразований превращается в соотношение

Как и в пункте б), сделав замену a = (3x – 1), b = 3y, мы получим уравнение a 2 + b 2 = 625, решения которого нам известны. Осталось понять, какие из них нам подходят, а какие — нет. Но это оказывается довольно просто: если c делится на 3, то из каждой четвёрки решений вида (c, d), (c, –d), (d, c), (–d, c) подходит ровно одно. В нашем случае, это (–8, 0), (–2, ±8), (7, ±5). И таким образом, на окружности, которая задана уравнением (5), лежит ровно 5 узлов клетчатой бумаги (рис. 3).

Замечание. Глядя на пять красных точек, изображённых на рис. 3, читатель может подумать, что если последовательно соединить их друг с другом, получится правильный пятиугольник. Однако это не так: у этого пятиугольника между собой равны только три стороны, а две другие немножко меньше. В действительности на клетчатой бумаге расположить правильный пятиугольник нельзя. Как и любой другой правильный многоугольник, за исключением квадрата.

Видео:Нахождение точек на числовой окружности. Дуги окружности 10 класс.Скачать

Послесловие

Придумав решение самостоятельно или ознакомившись с изложенным выше, читатель, наверное, задастся таким вопросом: правда ли, что какое натуральное число n мы ни возьмём, найдётся такая окружность, на которой лежит ровно n узлов клетчатой бумаги? Оказывается, это действительно так, причём методы построения этих окружностей не слишком отличаются от тех, которые мы уже видели. Вкратце изложим суть дела.

Ключевым моментом решения проблемы является следующая лемма.

Лемма. Уравнение x 2 + y 2 = 5 k имеет ровно 4(k + 1) целочисленных решений для любого целого неотрицательного k.

(На самом деле представленная лемма является частным случаем более общего факта. Именно, пусть r(n) обозначает число всевозможных способов представления натурального n в виде суммы квадратов пары целых чисел. Тогда можно доказать, что r(n) = d₁(n) – d₃(n), где d₁(n) и d₃(n) — числа, отвечающие количеству делителей n вида (4k + 1) и (4k + 3) соответственно.)

Для доказательства мы проверяем сначала, что утверждение леммы справедливо при k = 0 и k = 1. В самом деле, уравнение x 2 + y 2 = 1 имеет четыре целочисленных решения: (0, ±1) и (±1, 0). А уравнение x 2 + y 2 = 5 обладает ровно восемью корнями: (±2, ±1) и (±1, ±2).

Потом в дело вступает принцип математической индукции. С его помощью можно доказать, что при всех целых k > 1 уравнение x 2 + y 2 = 5 k имеет ровно восемь таких решений (x, y), что x и y не делятся на 5. Точно так же, как и корни уравнения x 2 + y 2 = 5, эти восемь пар чисел получаются друг из друга перестановкой x и y и изменениями знаков. А вместе с 4(k – 1) парами вида (5a, 5b), где (a, b) — решения уравнения a 2 + b 2 = 5 k –2 , они дают нам в точности 4(k + 1) решений исходного уравнения.

Теперь, вооружившись леммой, мы легко сможем дать ответ на поставленный вопрос. Из соображений симметрии ясно, что если расположить центр окружности в узле клетчатой бумаги (например, в начале координат), то количество лежащих на ней узлов будет делиться на четыре. А из леммы сразу вытекает, что если квадрат радиуса такой окружности равен 5 k , то на этой окружности лежит ровно 4(k + 1) узлов. В частности, на окружности x 2 + y 2 = 25 расположено ровно 12 узлов клетчатой бумаги.

В качестве примера окружности, на которой лежит произвольное наперёд заданное чётное число узлов клетчатой бумаги, мы можем взять окружность, заданную уравнением:

(6)

Чтобы убедиться в том, что она годится (то есть что на ней лежит 2(k + 1) узлов), достаточно повторить рассуждения из решения пункта б) и применить лемму. Если же хочется провести окружность через нечётное число узлов, то можно взять такую:

(7)

Используя лемму и свойства делимости на 3, можно доказать, что на ней лежит ровно (2k + 1) узлов, а выбирая подходящее k, это количество можно сделать любым наперёд заданным нечётным числом.

Окружности, которые задаются уравнениями (6) и (7), называются окружностями Шинцеля, по имени польского математика Анджея Шинцеля (Andrzej Schinzel). Отметим, что для данного натурального числа n эти уравнения задают, вообще говоря, не самую маленькую окружность с n узлами клетчатой бумаги на ней. Например, так происходит с n = 1 (очевидно, можно предъявить окружность сколь угодно маленького радиуса) или с n = 4 (здесь ясно, что существует окружность радиуса 1/√2. Менее тривиальный пример: n = 9. Соответствующая окружность Шинцеля имеет радиус 625/3, однако на окружности с центром (1/3, 0) и радиусом 65/3 также лежит ровно 9 узлов клетчатой бумаги.

Существуют также и менее тривиальные комбинации точек. Так, на рис. 4 изображена окружность с центром в точке (1/5, 2/5) и радиусом — на ней лежат четыре узла клетчатой бумаги: (–6, –2), (1, 7), (5, 5) и (2, –6). А на окружности с центром в точке (1/7, 2/7) и радиусом находятся пять узлов: , , , и (рис. 5).

Описание множества окружностей, которые проходят ровно через n узлов клетчатой бумаги для заданного натурального числа n, — пока нерешённая задача. Предполагается, что окружность, проходящая более чем через три узла, — достаточно редкое явление, то есть если провести окружность через три случайно выбранных узла клетчатой бумаги, то через четвёртый она пройдёт с малой вероятностью.

С этой задачей также связан вопрос об изображении круга на экране монитора. Будем считать, что экран представляет собой прямоугольный лист клетчатой бумаги, а круг на экране — объединение тех клеточек (пикселей), которые пересекаются со внутренностью круга. Тогда вопрос заключается в том, сколько различных изображений на экране имеет круг данного радиуса. Например, на рис. 6 представлено три различных изображения круга радиуса 4/5 (сторона клеточки, соответственно, равна единице). Полного ответа на этот вопрос пока тоже нет.

При подготовке данной публикации использовалась статья В. Вавилова и А. Устинова Окружности на решетках («Квант» №6, 2006), в которой обсуждаются некоторые свойства целочисленных решеток и расположение окружностей на них.