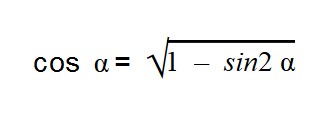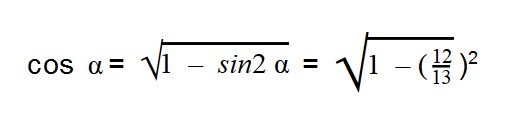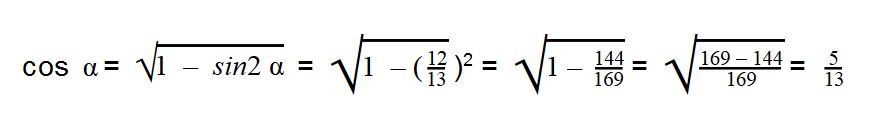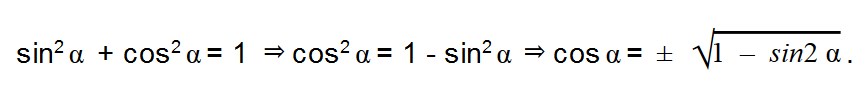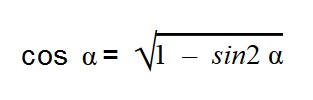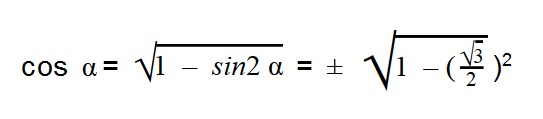Знание — сила. Познавательная информация
- sinx=0
- Тригонометрический круг: вся тригонометрия на одном рисунке
- А теперь подробно о тригонометрическом круге:
- Основное тригонометрическое тождество
- Связь между sin и cos одного угла
- Тангенс и котангенс через синус и косинус
- Связь между тангенсом и котангенсом
- Тангенс и косинус, котангенс и синус
- Примеры решения задач
- 📹 Видео
Видео:Как найти значения синуса и косинуса, НЕ запоминая!Скачать

sinx=0
Эта ассоциация позволяет легко запомнить, где синус равен 0, и быстро решить уравнение sin x=0.
Как обычно, частные случаи синуса рассматриваем на единичной окружности.
Используем ассоциацию косинус-колобок. Оба начинаются с ко-, в названии cos x буква o тоже косвенно на колобка указывает. Колобок движется по горизонтали. На координатной плоскости движение по горизонтали происходит вдоль оси x.
Поэтому cos x — это x, соответственно, sin x — это y.
Таким образом, чтобы найти, где синус равен 0, нужно выяснить, в каких точках y=0.
Раз y=0, то движения вверх-вниз не происходит.
На единичной окружности условию sin x=0 удовлетворяют две точки: 0 и π.
Чтобы из одной точки попасть в другую, надо пройти половину окружности, то есть π.
Поскольку таких точек, в которых синус равен 0, бесконечное множество, прибавляем не π, а πn, где n — целое число (то есть n принадлежит Z): x=0+πn.
Следовательно, решение уравнения sin x=0, есть множество точек
Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
Видео:Тригонометрическая окружность. Как выучить?Скачать

А теперь подробно о тригонометрическом круге:
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Основное тригонометрическое тождество
О чем эта статья:
9 класс, 10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Связь между sin и cos одного угла
Вы уже наверняка знаете, что тождественный — это равный.
Основные тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Это значит, что любую из этих функций можно найти, если известна другая функция.
Ключ к сердцу тригонометрии — основное тригонометрическое тождество. Запомните и полюбите его, чтобы отношения с тригонометрией сложились самым наилучшим образом:
sin 2 α + cos 2 α = 1
Из основного тождества вытекают равенства тангенса и котангенса, поэтому оно — ключевое.
Равенство tg 2 α + 1 = 1/cos 2 α и равенство 1 + сtg 2 α + 1 = 1/sin 2 α выводят из основного тождества, разделив обе части на sin 2 α и cos 2 α.
В результате деления получаем:
Поэтому основному тригонометрическому тождеству уделяется максимум внимания. Но какая же «метрия» может обойтись без доказательств. Видите тождество — доказывайте, не раздумывая.
sin 2 α + cos 2 α = 1
Сумма квадратов синуса и косинуса одного угла тождественно равна единице.
Чтобы доказать тождество, обратимся к теме единичной окружности.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат. Радиус единичной окружности равен единице.
Докажем тождество sin 2 α + cos 2 α = 1
- Итак, нам известны координаты точки A (1; 0).
Произвольный угол α, тогда cos α = x0 = ОB.
- Синус угла (sin α) — это отношение противолежащего катета к гипотенузе.
- Косинус угла (cos α) — это отношение прилежащего катета к гипотенузе.
Это значит, что точка A1 получает координаты cos α, sin α.
Образовался прямоугольный треугольник OA1B.
|OB| = |x|.
Гипотенуза OA1 имеет значение, равное радиусу единичной окружности.
|OA1| = 1.
Применяя полученное выражение, записываем равенство по теореме Пифагора, поскольку получившийся угол — прямой:
|A1B| 2 + |OB| 2 = |OA1| 2 .
Записываем в виде: |y| 2 + |x| 2 = 1 2 .
Это значит, что y 2 + x 2 = 1.
sin угла α = y
cos угла α = x
Вставляем данные угла вместо координат точек:
OB = cos α
A1B = sin α
A1O = 1
Что и требовалось доказать.
Основное тригонометрическое тождество связывает синус угла и косинус угла. Зная одно, вы легко можете найти другое. Нужно лишь извлечь квадратный корень по формулам:
- sin α = ±
- cos α = ±
Как видите, перед корнем может стоять и минус, и плюс. Основное тригонометрическое тождество не дает понять, положительным или отрицательным был исходный синус/косинус угла.
Как правило, в задачках с подобными формулами уже есть условия, которые помогают определиться со знаком. Обычно такое условие — указание на координатную четверть. Таким образом без труда можно определить, какой знак нам требуется.
Видео:ЗНАЧЕНИЯ СИНУСА И КОСИНУСА НА ОКРУЖНОСТИСкачать

Тангенс и котангенс через синус и косинус
- Синус угла — это ордината y.
- Косинус угла — это абсцисса x.
- Тангенс угла — это отношение ординаты к абсциссе.
- Котангенс угла — это отношение абсциссы к ординате.
Из всего этого множества красивых, но не сильно понятных слов, можно сделать вывод о зависимости одного от другого. Такая связь помогает отдельно преобразовывать нужные величины.
- tg α =
- ctg α =
Исходя из определений:
- tg α =
=
- ctg α =
=
Это позволяет сделать вывод, что тригонометрические тождества

задаются sin и cos углов.
Отсюда следует, что тангенс угла — это отношение синуса угла к косинусу. А котангенс угла — это отношение косинуса к синусу.
Отдельно стоит обратить внимание на то, что тригонометрические тождества

верны для всех углов α, значения которых вписываются в диапазон.
- Например, выражение
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
применимо для любого угла α, не равного π * z, где z — это любое целое число.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео:17 вариант-ЕГЭпрофиль-Реальный-с Оформлением на 100Скачать

Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
- Тождество записывается в следующем виде:
tg α * ctg α = 1.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
ctg α = x/y
 и
и  ,
, получаем:

Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Видео:Таблица значений тригонометрических функций - как её запомнить!!!Скачать

Тангенс и косинус, котангенс и синус
Все тождества выше позволяют сделать вывод, что тангенс угла связан с косинусом угла, а котангенс угла — с синусом.
Эта связь становится очевидна, если взглянуть на тождества:
- tg 2 α + 1 =
Сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла.
- 1 + ctg 2 α =
Сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла.
Вывести оба этих тождества можно из основного тригонометрического тождества:
sin 2 α + cos 2 α = 1.
- Для этого нужно поделить обе части тождества на cos 2 α, где косинус не равен нулю.
- В результате деления получаем формулу tg 2 α + 1 =
- Если обе части основного тригонометрического тождества sin 2 α + cos 2 α = 1 разделить на sin 2 α, где синус не равен нулю, то получим тождество:
1 + ctg 2 α =.
- Отсюда можно сделать вывод, что тригонометрическое тождество tg 2 α + 1 =
применимо для любого угла α, не равного
+ π + z, где z — это любое целое число.
- А тригонометрическое тождество 1 + ctg 2 α =
применимо для любого угла, не равного π * z, где z — это любое целое число.
Хорошо бы выучить все формулы и запомнить формулировки тождеств наизусть. Чтобы это сделать, сохраняйте себе табличку с основными формулами.
Основные тригонометрические тождества
sin 2 α + cos 2 α = 1
tg 2 α + 1 =
1 + ctg 2 α =
Чтобы тратить еще меньше времени на решение задач, сохраняйте таблицу значений тригонометрических функции углов, которые чаще всего встречаются в задачах.
Видео:Тригонометрия. Значения синуса и косинуса углов 0°,90°,180°, 270 °, 360° . 10-11 классСкачать

Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:
Вычисляем:
Нам известны значения sin α и cos α, поэтому можно легко найти тангенс, используя формулу:
Таким же образом, используя формулу, вычисляем значение котангенса:
Задачка 2. Найдите значение cos α,
если:
- Чтобы решить задачу, необходимы следующие тригонометрические тождества:
Выражаем cos α из тригонометрической единицы:
Далее подставляем значения sin α:

Подставляем значения sin α:
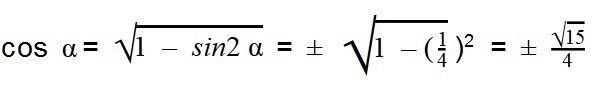
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
📹 Видео
Синус, косинус, тангенс и котангенс углов от 0 до 180 градусов.Скачать
Как видеть тангенс? Тангенс угла с помощью единичного круга.Скачать

ТРИГОНОМЕТРИЯ ЗА 10 МИНУТ — Синус, Косинус, Тангенс, Котангенс // Подготовка к ЕГЭ по МатематикеСкачать

10 класс, 13 урок, Синус и косинус Тангенс и котангенсСкачать

🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Как запомнить значения синусов и косинусов?! #математика #синус #косинус #геометрия #егэ #shortsСкачать

Как просто запомнить, что такое sin, cos, tg?! #косинус #синус #тангенс #математика #огэ #егэСкачать

Тригонометрическая окружность для непонимающихСкачать

Формулы приведения - как их легко выучить!Скачать

Простейшие тригонометрические уравнения. y=sinx. 1 часть. 10 класс.Скачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

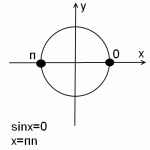





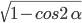
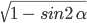
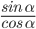
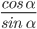
 =
= 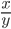 =
= 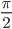 + π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.
+ π + z, где z — это любое целое число. В противном случае, в знаменателе будет стоять 0.