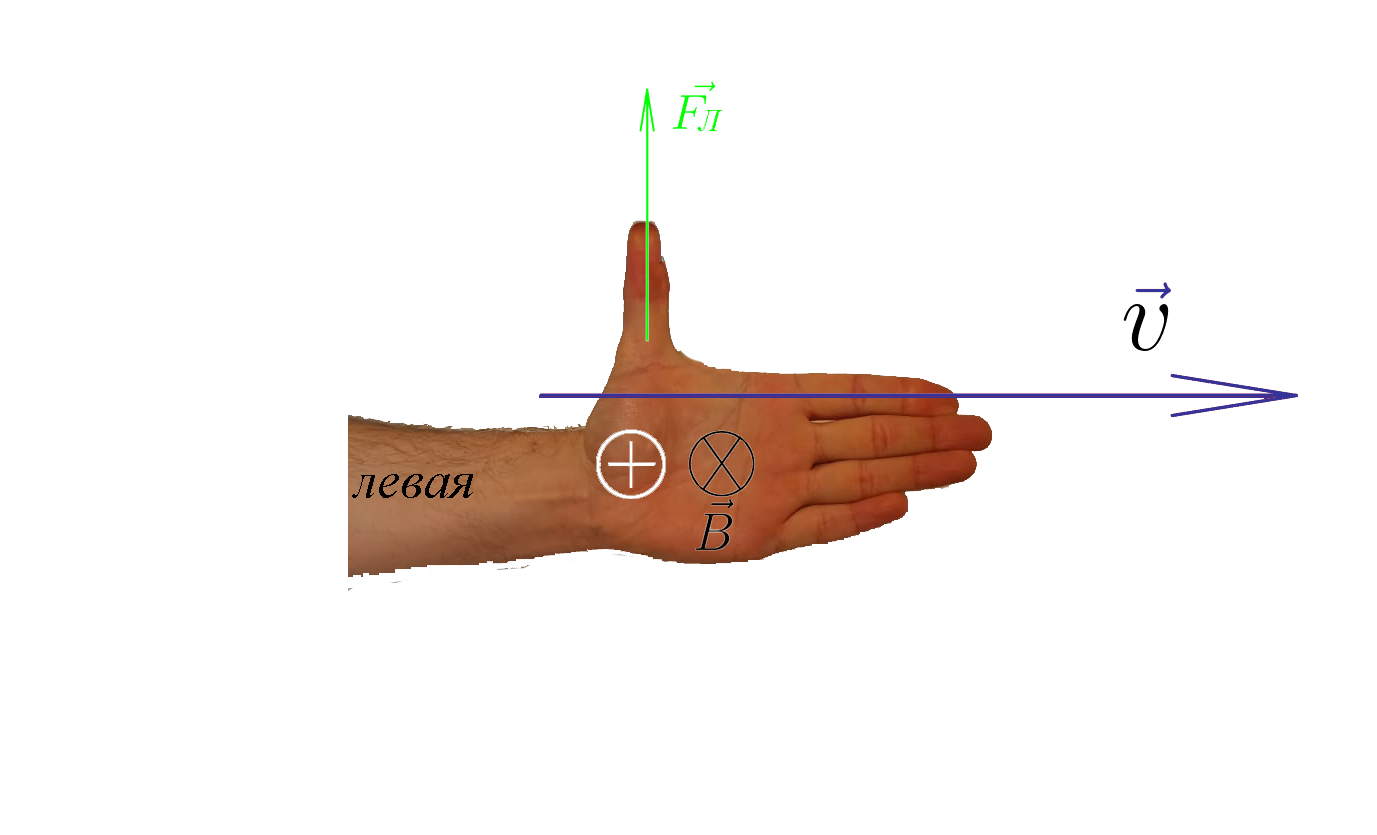
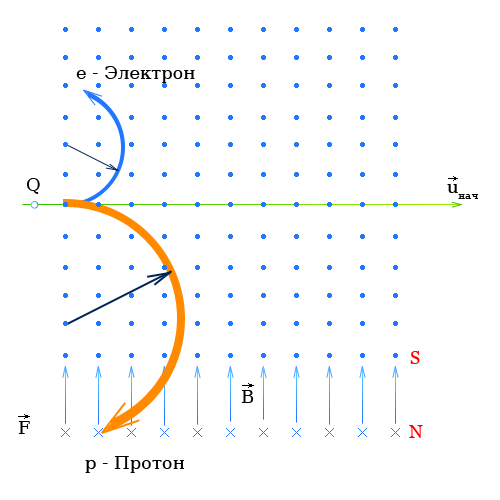
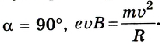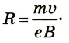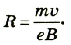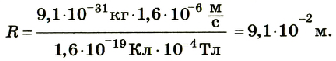- Сила Лоренца действующая на электрон
- Вычислить, найти силу Лоренца действующую на электрон или протон
- Радиус траектории электрона в магнитном поле
- Сила Лоренца действующая на протон
- Радиус траектории протона в магнитном поле
- Сила Лоренца — основные понятия, формулы и определение с примерами
- Сила Лоренца:
- Как определить направление силы Лоренца
- Что такое сила Лоренца
- Пример решения задачи
- Сила Лоренца .
- Направление силы Лоренца, действующей на положительно заряженную частицу .
- 🎥 Видео
Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

Сила Лоренца действующая на электрон
В частном случае носителем заряда является электрон. Тогда в формулу (5) в качестве Q следует подставить
При определении направления движения электронов с помощью правила левой руки следует учитывать, что направление движения электронов противоположно техническому направлению тока.
Величина и направление силы Лоренца определяются соотношением
где $vector$, $vector$ и $vector$ образуют правую систему.
Для электронов, движущихся перпендикулярно магнитному полю, формула упрощается:
Так как сила действует перпендикулярно скорости и направлению поля, она создает центростремительное ускорение, т.е. изменяет направление скорости, не меняя ее величины. Поэтому электрон движется в магнитном поле по окружности.
Видео:Галилео. Эксперимент. Сила ЛоренцаСкачать

Вычислить, найти силу Лоренца действующую на электрон или протон
Видео:Сила ЛоренцаСкачать

Радиус траектории электрона в магнитном поле
Для определения радиуса круговой траектории электрона приравняем силу Лоренца и центростремительную силу.
| r | радиус круговой траектории электрона, | метр |
|---|---|---|
| me | 9,11 · 10 -31 кг — масса электрона, | кг |
| e | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость электрона, | м/с |
| B | магнитная индукция, | Тесла |
то, приравнивая обе силы, получаем
При больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя электронов me, а необходимо учитывать релятивистское увеличение массы.
Видео:Движение электронов в магнитном поле - Сила ЛоренцаСкачать

Сила Лоренца действующая на протон
Электрический заряд протона равен по модулю заряду электрона, но имеет положительный знак.
При определении направления движения протонов с помощью правила левой руки направление движения протонов совпадает с техническим направлением тока и с картинкой.
Таким образом электрон и протон влетая в магнитное поле в одном направлении будут отклоняться в разные стороны.
Величина силы действующая на электрон и на протон будет одинакова (определяется формулой №3), но поскольку протон гораздо тяжелее электрона, радиус закручивания для протона будет больше.
Видео:Действие магнитного поля на движущийся заряд. Сила Лоренца | Физика 11 класс #3 | ИнфоурокСкачать

Радиус траектории протона в магнитном поле
| r | радиус круговой траектории протона, | метр |
|---|---|---|
| mp | 1,67 · 10 -27 кг — масса протона, | кг |
| p | 1,602 · 10 -19 Кл — элементарный электрический заряд, | Кулон |
| v | скорость протона, | м/с |
| B | магнитная индукция, | Тесла |
Радиус траектории для протона будет вычисляться по аналогичной формуле
Из этой формулы видно что при одинаковых скоростях электрона и протона радиус траектории протона будет значительно больше, чем у электрона пропорционально отношению масс этих частиц
Аналогично при больших значениях скорости (выше примерно 2 · 10 7 м/с) в расчетах нельзя использовать массу покоя протонов mp, а необходимо учитывать релятивистское увеличение массы.
Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Сила Лоренца — основные понятия, формулы и определение с примерами
Содержание:
Сила Лоренца:
Центростремительное (нормальное) ускорение появляется при криволинейном движении тела и характеризует скорость изменения направления скорости с течением времени. Оно вычисляется по формуле
Согласно закону Ампера на проводник с током в магнитном поле действует сила, которую можно рассматривать как результат действия магнитного поля на все движущиеся в проводнике заряды. Отсюда можно сделать вывод, что магнитное поле оказывает силовое действие на каждый движущийся заряд.
По закону Ампера на проводник длиной
Поскольку электрический ток — направленное движение заряженных частиц, то силу тока можно представить в виде 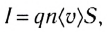
где q — величина заряда одной частицы, n — концентрация заряженных частиц (число частиц в единице объема проводника), 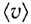
Тогда 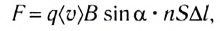
где 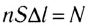
Разделив модуль силы F на число частиц N, получим модуль силы, действующей на один движущийся заряд со стороны магнитного поля:
где v — модуль скорости движущегося заряда.
Выражение для силы, с которой магнитное поле действует на движущийся заряд, в 1895 г. впервые получил голландский физик Хендрик Антон Лоренц. В его честь эта сила называется силой Лоренца:
Видео:Правило рук 👋 КАК ЛЕГКО определять НАПРАВЛЕНИЕ ЛИНИЙ МАГНИТНОГО ПОЛЯ??Скачать

Как определить направление силы Лоренца
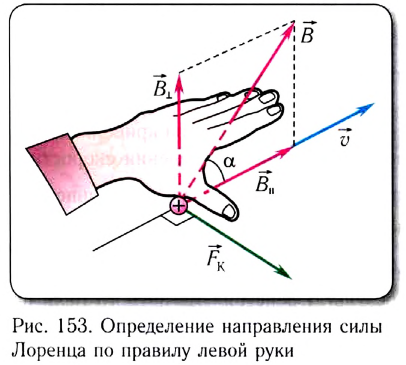
Направление силы Лоренца определяется по правилу левой руки (рис. 153):
если левую руку расположить так, чтобы перпендикулярная к скорости 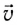
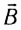
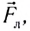
Поскольку сила Лоренца перпендикулярна вектору скорости, то она не может изменить модуль скорости, а изменяет только ее направление и, следовательно, работы не совершает.
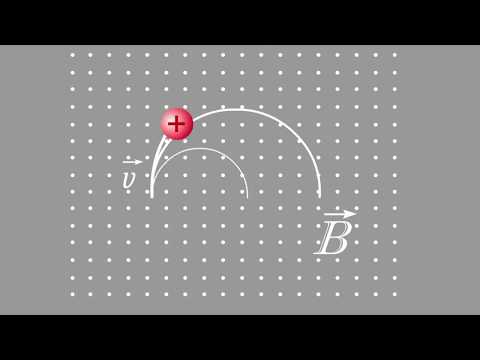
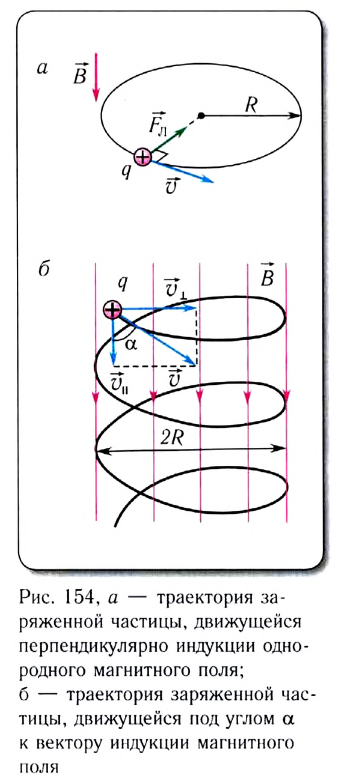
Таким образом, если поле однородно, то при движении частицы перпендикулярно к магнитной индукции поля ее траекторией будет окружность (рис. 154, а), плоскость которой перпендикулярна к магнитному полю.
Ускорение частицы 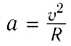
и радиус окружности
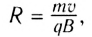
описываемой частицей в магнитном поле.
Если скорость направлена под углом к индукции магнитного поля, движение заряда можно представить в виде двух независимых движений (рис. 154, б):
- равномерного вдоль поля со скоростью
(
— составляющая вектора скорости, параллельная вектору индукции
магнитного поля);
- по окружности радиусом R в плоскости, перпендикулярной к вектору
, с постоянной по модулю скоростью
(
— составляющая вектора скорости, перпендикулярная вектору индукции
магнитного ноля).
В результате сложения обоих движений возникает движение по винтовой линии, ось которой параллельна магнитному полю (см. рис. 154, б). Период этого движения определяется по формуле
Действие силы Лоренца широко применяется в различных электротехнических устройствах:
- электронно-лучевых трубках телевизоров и дисплеев;
- ускорителях заряженных частиц (циклотронах);
- масс-спектрометрах — приборах, определяющих отношение зарядов частиц к их массе по радиусу окружности, описываемой ими в магнитном поле;
- магнитогидродинамических генераторах ЭДС (МГД-генератор — устройство для генерации электрических токов, использующее проводящие жидкости, движущиеся в магнитном поле).
Видео:Сила ЛоренцаСкачать

Что такое сила Лоренца
Силой Лоренца FЛ называют силу, действующую на электрически заряженную частицу, двигающуюся в электромагнитном поле, определяя действия на нес электрической» и магнитного полей одновременно. Это выражается формулой:
где 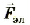
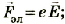
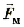
Сила Лоренца действует на движущуюся электрически заряженную частицу в электромагнитном поле.
Для упрощения рассмотрим случай, когда 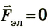
Выясним, как можно рассчитать силу, действующую на движущуюся заряженную частицу в магнитном поле. Как известно, электрический ток в проводнике — это упорядоченное движение заряженных частиц. Согласно электронной теории сила тока рассчитывается по формуле:
где I — сила тока; е — заряд частицы; 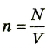
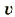
Действие магнитного поля на проводник с током является действием магнитного поля на все движущиеся заряженные частицы. Поэтому формулу силы Ампера можно записать с учетом выражения силы тока в электронной теории:
Если учесть, то
Если сила Ампера является равнодействующей всех сил, действующих на N частиц, то на одну частицу будет действовать сила в N раз меньше:
Это и есть формула для расчета магнитной составляющей силы Лоренца:
Магнитная составляющая силы Лоренца
Анализ этой формулы позволяет сделать выводы, что:
- магнитная составляющая силы Лоренца действует только на движущуюся частицу (
≠ 0);
- магнитная составляющая не действует на движущуюся частицу, которая движется вдоль линии магнитной индукции (а = 0).
Направление магнитной составляющей силы Лоренца, как и силы Ампера, определяется по правилу левой руки. При этом необходимо учитывать, что это справедливо для положительно заряженных частиц. Если определять направление силы Лоренца, действующей на электрон или другую отрицательно заряженную частицу, то, применяя правило левой руки, нужно мысленно изменять направление движения на противоположное.
Сила Лоренца направлена всегда под некоторым углом к скорости частицы, поэтому она придает ей центростремительное ускорение (рис. 2.15).
Для случая, если
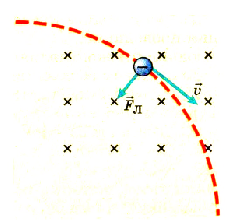
Рис. 2.15. Сила Лоренца придает частице центростремительное ускорение
Таким образом, заряженная частица, попадая в магнитной поле, начинает двигаться по дуге окружности. При иных значениях α ≠ О траектория движения частицы в магнитном поле приобретает форму спирали.
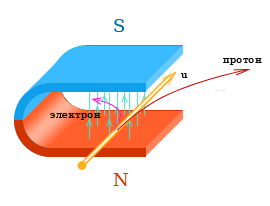
Наблюдать действие силы Лоренца можно с помощью электронно-лучевой трубки, которая есть во многих осциллографах (рис. 2.16), Если включить питание осциллографа, то на его экране можно увидеть светлое пятно, появившееся в месте падения электронов на экран. Если теперь сбоку поднести к трубке постоянный магнит, то пятно сместится, что подтверждает действие магнитного поля на движущиеся электроны.
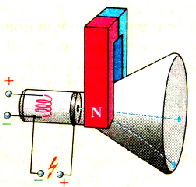
Рис. 2.16. Магнитное поле смещает электронный пучок в трубке осциллографа
Действие силы Лоренца применяется во многих приборах и технических установках. Так, смещение электронного луча, который «рисует» изображение на экране вакуумного кинескопа телевизора или дисплея компьютера, совершается магнитным полем специальных катушек, в которых проходит электрический ток, изменяющийся во времени по определенному закону,
В научных исследованиях применяют так называемые циклические ускорители заряженных частиц, в них магнитное поле мощных электромагнитов удерживает заряженные частицы на круговых орбитах.
Весьма перспективными для развития электроэнергетики являются магнито-гидродипамические генераторы (МГД-генераторы) (рис. 2.17). Поток высокотемпературного газа (плазмы), который образуется при сгорании органического топлива и имеет высокую концентрацию ионов обоих знаков, пропускается через магнитное ноле.
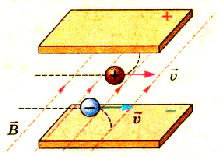
Puc. 2.17. Схема, объясняющая действие МГД-генератора
Вследствие действия силы Лоренца ионы отклоняются от прежнего направления движения и оседают на специальных электродах, сообщая им определенный заряд. Полученную при этом разность потенциалов можно использовать для получения электрического тока. Такие установки в будущем могут существенно повысить КПД тепловых «электростанций за счет выработки дополнительной электроэнергии при прохождении газов, которые после выхода из топки имеют довольно высокую температуру и высокую ионизацию, через MГД-генераторы.
Пример решения задачи
Электрон влетает в однородное магнитное поле с индукцией 10 -4 Тл перпендикулярно к линиям магнитной индукции. Его скорость 1.6 . 10 6 м/с. Найти радиус окружности, по которой движется электрон.
| Дано: В = 10 -4 Тл,  = 1,6 ∙ 10 -6 м/с, = 1,6 ∙ 10 -6 м/с, е = 1,6 • 10 -19 Кт, 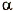 = 90°. = 90°. | Peшение Сила Лоренца в данном случае действует под прямым углом к скорости движения электрона, не изменяя его скорости. Поэтому она придает электрону центростремительное ускорение. Таким образом, можно записать: 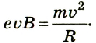 |
| R-? |
Отсюда
Подставим значения физических величин:
Ответ: электрон будет двигаться по круговой орбите, радиус которой 9,1 ∙ 10 -2 м.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Правило Буравчика в физике
- Шунт и добавочное сопротивление
- Электродвижущая сила
- Электрические измерительные приборы
- Закон Ома для полной цепи
- Закон Ома для цепи переменного тока с последовательным соединением сопротивлений
- Сила и закон Ампера
- Закон взаимодействия прямолинейных параллельных проводников с током
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Сила Ампера | Сила Лоренца | ЕГЭ Физика | Николай НьютонСкачать

Сила Лоренца .
Сила Лоренца действует на заряженную частицу, движущуюся в магнитном поле.
( F_л=Bqv cdot sin alpha )
(B) -магнитная индукция, единица измерения Тесла [Тл]
(q) — заряд частицы, единица измерения Кулон [Кл] )
(v) — скорость частицы
( alpha )- угол между вектором магнитной индукции ( vec ) и вектором скорости частицы ( vec )
Видео:Магнитное поле движущихся зарядов 1980 гСкачать

Направление силы Лоренца, действующей на положительно заряженную частицу .
Если вектор магнитной индукциии входит в ладонь левой руки, а четыре пальца сонаправлены с направлением вектора скорости положительно заряженной частицы, то отогнутый на ( 90^0 ) большой палец показывает направление силы Лоренца действующей на эту частицу.
Задача 1. (Сила Лоренца)
Пылинка, имеющая заряд (q=10^ Кл) движется в магнитном поле с индукцией (B=20 Тл) . Скорость пылинки перпендикулярна линиям магнитной индукции и равна (100 м/с ) Вычислить значение силы Лоренца, действующей на пылинку со стороны магнитного поля. Дать ответ в миллиньютонах.
🎥 Видео
Действие магнитного поля на движущийся заряд Сила Лоренца Урок 81Скачать

сила Лоренца | правило левой руки | физика 11 классСкачать

Урок 278. Задачи на силу Лоренца - 1Скачать

Физика. 10 класс. Сила Лоренца. Движение заряженной частицы в магнитном поле /12.04.2021/Скачать

3800 задач для школьников. Сила Лоренца 13.51-13.64Скачать

Урок 279. Задачи на силу Лоренца - 2Скачать
Сила Лоренца в электрогенераторе и электродвигателеСкачать

Электрон в магнитном полеСкачать

15. Сила Ампера. Сила Лоренца. Правило левой руки. ( русс яз)Скачать

Использование силы ЛоренцаСкачать
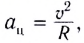
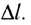
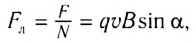

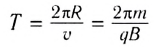
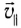 (
( 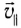 — составляющая вектора скорости, параллельная вектору индукции
— составляющая вектора скорости, параллельная вектору индукции 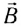 магнитного поля);
магнитного поля);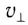 (
( 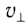 — составляющая вектора скорости, перпендикулярная вектору индукции
— составляющая вектора скорости, перпендикулярная вектору индукции 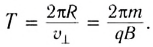
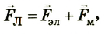
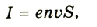
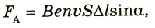
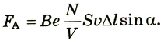
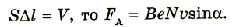
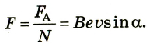
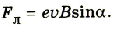

 ≠ 0);
≠ 0);