Правила построения сечений многогранников:
1) проводим прямые через точки, лежащие в одной плоскости;
2) ищем прямые пересечения плоскости сечения с гранями многогранника, для этого
а) ищем точки пересечения прямой принадлежащей плоскости сечения с прямой, принадлежащей одной из граней (лежащие в одной плоскости);
б) параллельные грани плоскость сечения пересекает по параллельным прямым.
Примеры построения сечений:
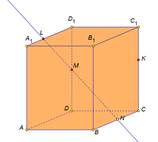
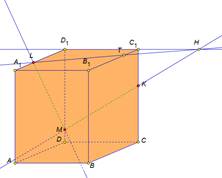
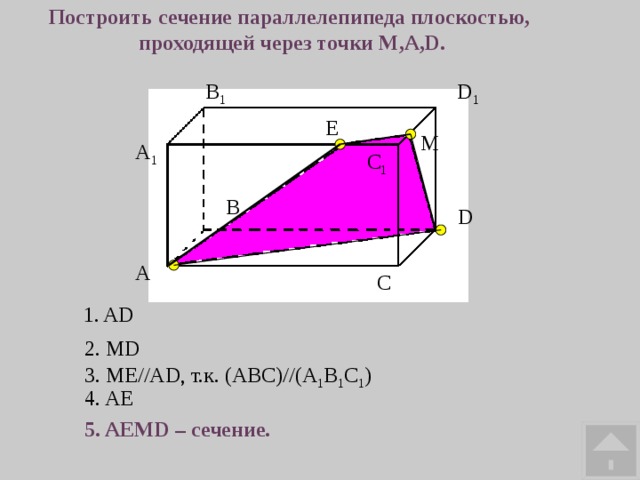
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Построим сечение, проходящее через точки M, N, L.
Соединим точки M и L, лежащие в плоскости AA1D1D.
Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.
Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.
Соединим точки K и M, лежащие в одной плоскости AA1B1B.
Найдем прямую пересечения плоскости сечения с плоскостью DD1C1C:
пересечем прямую ML (принадлежащую сечению) с ребром DD1, они лежат в одной плоскости AA1D1D, получим точку X2;
пересечем прямую KN (принадлежащую сечению) с ребром D1C1, они лежат в одной плоскости A1B1C1D1, получим точку X3;
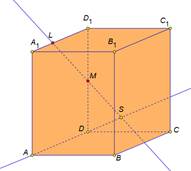
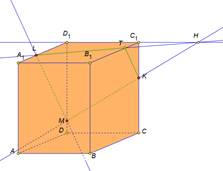
Точки X2 и X3 лежат в плоскости DD1C1C. Проведем прямую X2 X3 , которая пересечет ребро C1C в точке T, а ребро DC в точке P. И соединим точки L и P, лежащие в плоскости ABCD.
MKNTPL — искомое сечение.
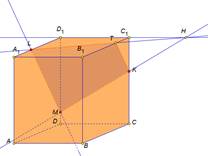
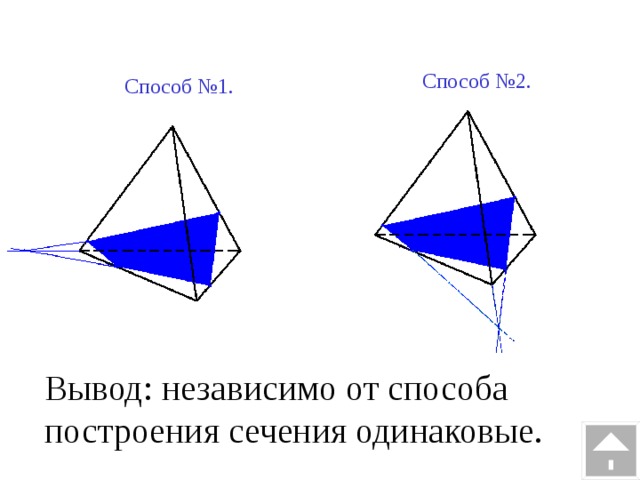
Рассмотрим ту же самую задачу на построение сечения, но воспользуемся свойством параллельных плоскостей. Это облегчит нам построение сечения.

Соединим точки M и L, лежащие в плоскости AA1D1D.

Через точку N, проведем прямую NT параллельную прямой ML. Прямые NT и ML лежат в параллельных плоскостях по свойству параллелепипеда.

Пересечем прямую ML ( принадлежащую сечению) с ребром A1D1, они лежат в одной плоскости AA1D1D. Получим точку X1.

Точка X1 лежит на ребре A1D1, а значит и плоскости A1B1C1D1, соединим ее сточкой N, лежащей в этой же плоскости.
X1 N пересекается с ребром A1B1 в точке К.

Соединим точки K и M, лежащие в одной плоскости AA1B1B.

Проведем прямую TP через точку T, параллельно прямой KM ( они лежат в параллельных плоскостях).

Соединим точки P и L ( они лежат в одной плоскости).

Видео:10 класс, 14 урок, Задачи на построение сеченийСкачать

Виды сечений параллелепипеда
Решение задач на построение сечений
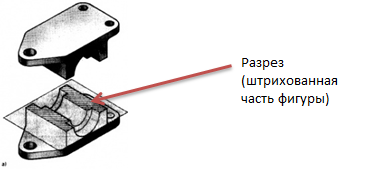
| Подумайте, какой школьный предмет позволяют научиться правильно выполнять и оформлять чертежи, познакомится с различными графическими способами передачи сведений об объектах предметного мира. Правильно! Это черчение. Для изготовления деталей на заводе используются точные чертежи этих деталей в разрезе. Разрезы используются для показа внутренней формы изделия. Разрезом называется изображение, полученное при мысленном рассечении детали одной или несколькими секущими плоскостями. В разрезах показывается то, что получается в секущей плоскости. | На экране изображение  На экране изображение На экране изображение  На экране рисунок На экране рисунок
| ||||||||||||
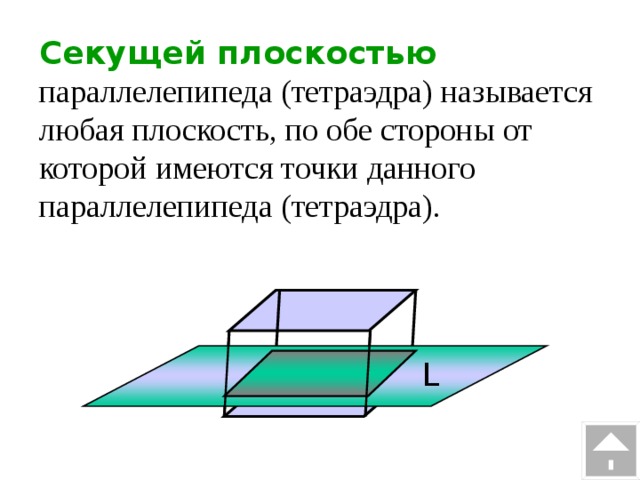
| При решении геометрических задач связанных с тетраэдром и параллелепипедом тоже иногда необходимо построить разрез фигуры. Только полученное изображение в геометрии называется сечением. Давайте разберёмся, что называется сечением тетраэдра и параллелепипеда. | |||||||||||||
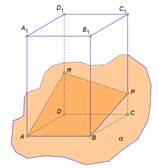
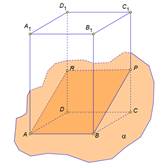
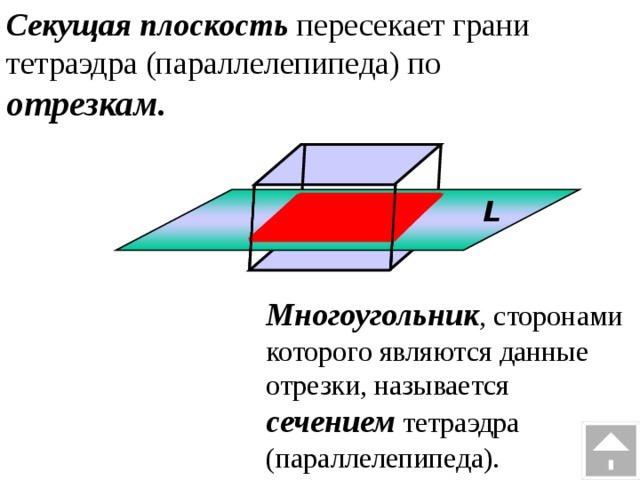
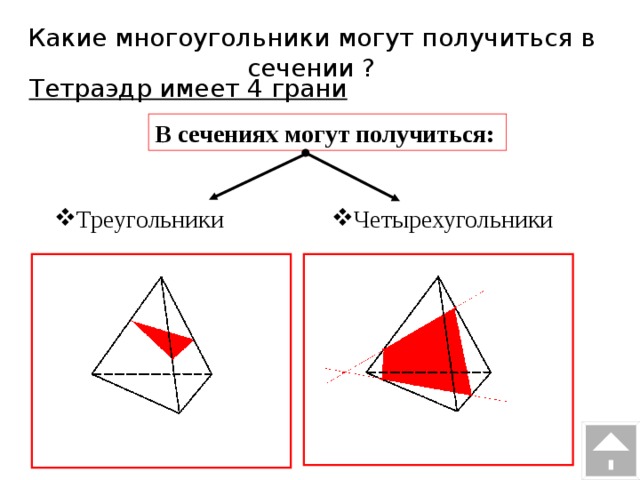
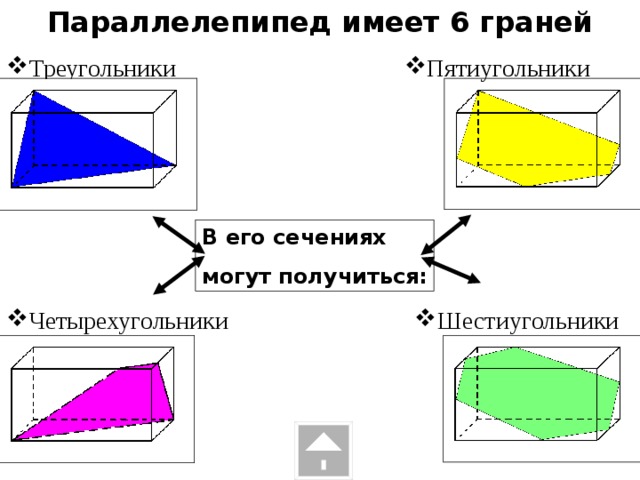
| Секущая плоскость α пересекает грани тетраэдра по отрезкам АЕ, ЕС, АС. Треугольник АЕС, сторонами которого являются эти отрезки, называется сечением тетраэдра. Тетраэдр имеет четыре грани, значит его сечениями могут быть только треугольники и четырехугольник. При пересечении параллелепипеда секущая плоскость также оставляет следы на его боковых гранях в виде отрезков. Отрезки образуют многоугольник, который называется сечением параллелепипеда. Так как у параллелепипеда шесть граней, то в сечении может получиться фигура треугольник, на рисунке вы это видите. Четырехугольник Пятиугольник и шестиугольник . При построении сечений очень легко нарушить геометрические факты, теоремы. Например, данное сечение параллелепипеда плоскостью содержит ошибку. Если плоскость пересекает две параллельные плоскости, то линии их пересечения параллельны. Значит, отрезок АВ и отрезок RP на чертеже должны быть изображены параллельно. А мы наблюдаем, что это не так . Но и отрезки AR и BP тоже не параллельны, хотя лежат в параллельных плоскостях. Значит плоскость α, должна пересекать грани АА1D1D и BB1C1C по параллельным прямым. Исправим ошибки. Или на данном чертеже прямая LM пересекает ребро ВC в точке N. Но это невозможно. Прямая LM принадлежит плоскости АА1D1D, а прямая ВС не лежит в данной плоскости, значит они не могут пересекаться, они скрещивающиеся прямые. Так прямая LM не может пересекать DC, ВВ1 , а вот c прямой AD они пересекаются. Исправим ошибку на чертеже. | На экране текст и изображение: Сечение тетраэдра 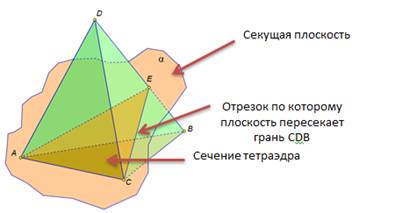 На экране изображение и текст: Виды сечений тетраэдра На экране изображение и текст: Виды сечений тетраэдра
На экране изображение и текст: Сечение параллелепипеда На экране изображение и текст: Виды сечений параллелепипеда
На экране изображение: На экране обновляется изображение На экране обновляется чертёж | ||||||||||||
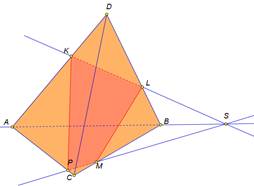
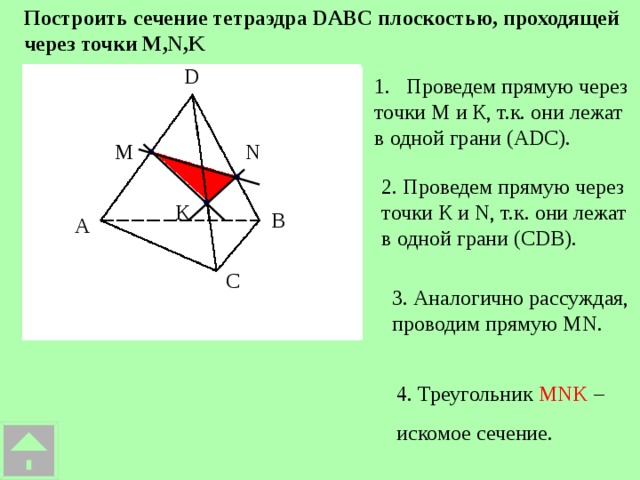
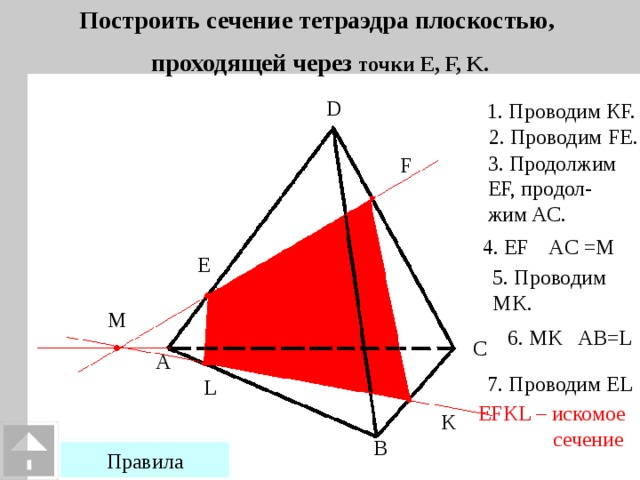
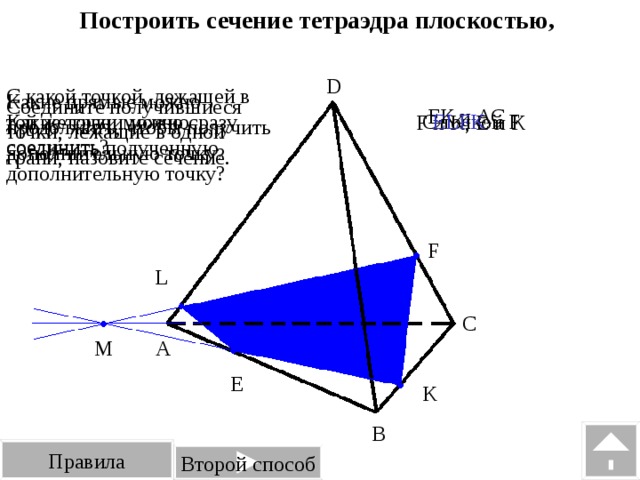
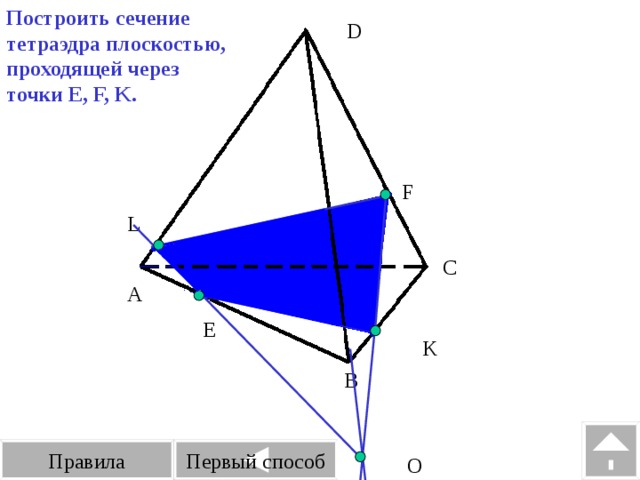
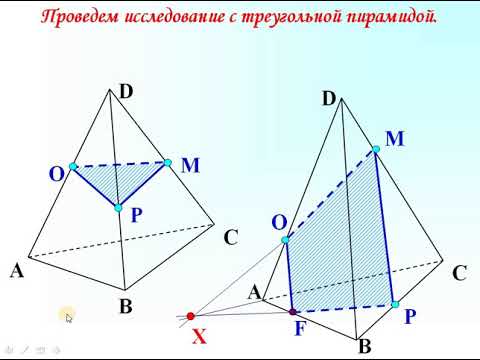
| Рассмотрим примеры построения различных сечений. Дан тетраэдр АВСD . На его рёбрах отмечены точки K,L,M. Построить сечение тетраэдра плоскостью, проходящей через точки K,L,M. Изобразим тетраэдр и данные точки. При построении сечений нужно помнить один факт, что если две плоскости имеют общие точки, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Так у нас секущая плоскость проходит чрез точки M,L, а они лежат в плоскости CDB, значит ML-линия пересечения плоскостей. Аналогично прямая KL является линией пересечения секущей плоскости и грани ADB Для того чтобы построить линию пересечения с гранью АВС нужны две точки. Точка М уже у нас есть. Для построения второй точки. Продлим до пересечения прямые KL и АВ. Отметим их общую точку S. Точка S принадлежит секущей плоскости, так как ей принадлежит прямая KL и принадлежит грани АВС, так как ей принадлежит прямая АВ. Значит секущая плоскость пересекает плоскость АВС по прямой MS. Построим эту прямую. Отметим точку P- точку пересечения прямой с ребром АС. Отрезок PM- след от сечения грани плоскостью α. Мы получили в результате две точки K и Р В грани АDC. Отрезок КР есть линия пересечения секущей плоскости и грани. Проведем этот отрезок. Четырехугольник KLMP-искомое сечение. | На экране текст. Дан тетраэдр АВСD . На его рёбрах отмечены точки K,L,M. Построить сечение тетраэдра плоскостью, проходящей через точки K,L,M. На экране изображение. 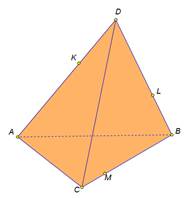 На экране изображение. На экране изображение. 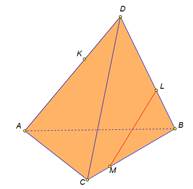 На экране изображение. На экране изображение. 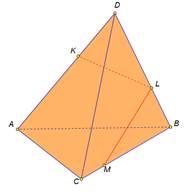 На экране изображение. На экране изображение. 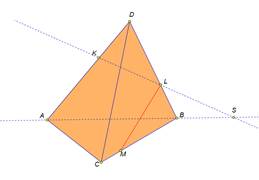 На экране изображение. На экране изображение. 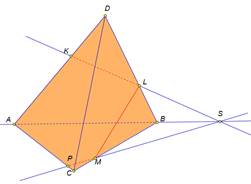 На экране изображение. На экране изображение. 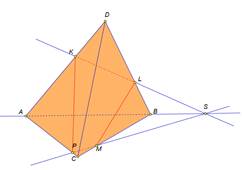 На экране изображение На экране изображение
| ||||||||||||
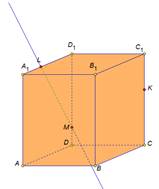
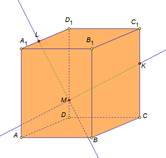
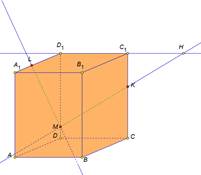
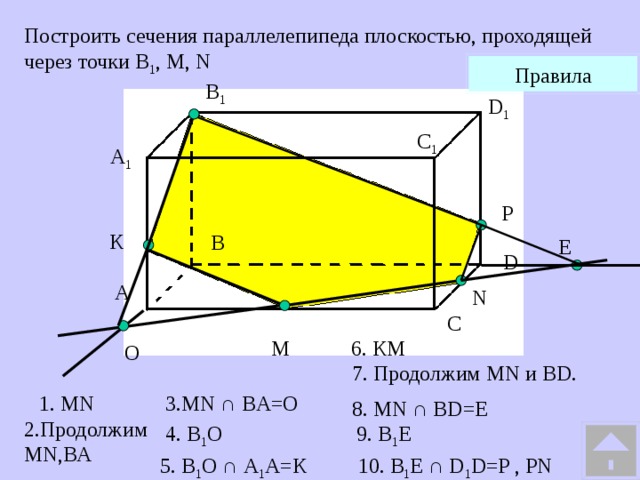
| Рассмотрим задачу на построение сечения параллелепипеда. На рёбрах параллелепипеда даны точки K,L,M. Построить сечение параллелепипеда плоскостью KLM. Построим данный параллелепипед и отметим указанные точки. Так как точки L и M принадлежат грани АА1D1D и секущей плоскости, значит прямая LM их линия пересечения, а отрезок LM след от сечения грани АА1D1D секущей плоскостью. Аналогично в грани DD1C1C построим прямую MK и выделим отрезок MK. В грани А1B1C1D1 есть только одна точка L, для построения второй точки продлим до пересечения прямые D1C1 и MK. Отметим их общую точку H. Точка H принадлежит секущей плоскости, так принадлежит прямой MK. И принадлежит грани A1B1C1D1, так как принадлежит прямой D1C1. Проведем прямую LH. Отметим точку T точку пересечения прямой с ребром B1C1. Выделим отрезок LT это будет след от сечения плоскость. Так как точки T и К принадлежат секущей плоскости и грани ВВ1С1С, то отрезок ТК будет следом от сечения в этой грани. Выделим получившийся четырехугольник KMLT. Это искомое сечение. Рассмотренные задачи относятся к классу задач на построение и имеют свои этапы решения: анализ, построение, доказательство. Мы рассмотрели только этап построения, так как наша цель– научиться строить искомое сечение. | На экране текст: На рёбрах CC1,A1D1, DD1 параллелепипеда АВСDA1B1C1D1 отмечены точки K,L,M соответственно. Построить сечение параллелепипеда плоскостью KLM. На экране изображение: 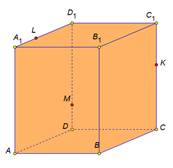 На экране изображение: На экране изображение:
На экране изображение и и текст:
На экране изображение и текст:
На экране изображение и текст:
На экране изображение:
На экране изображение:
Комментарий: задачи разобраны очень подробно, оформлены, четко структурированы. были небольшие опечатки по ходу решения. Видео:СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать  Построение сечений в тетраэдре и параллелепипеде. Построение сечений в тетраэдре и параллелепипеде. Просмотр содержимого документа |









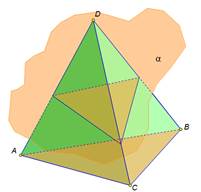 В сечении тераэдра плоскостью лежит треугольник
В сечении тераэдра плоскостью лежит треугольник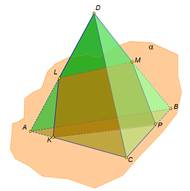 В сечении тетраэдра плоскостью лежит четырёхугольник
В сечении тетраэдра плоскостью лежит четырёхугольник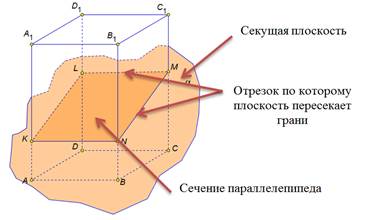
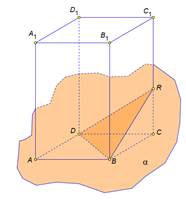 В сечении паралелепипеда плоскостью лежит треугольник
В сечении паралелепипеда плоскостью лежит треугольник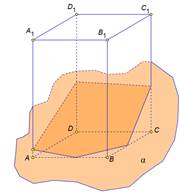 В сечении паралелепипеда плоскостью лежит пятьугольник
В сечении паралелепипеда плоскостью лежит пятьугольник