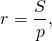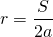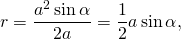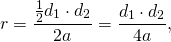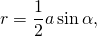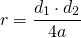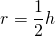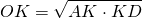В данной публикации мы рассмотрим определение, свойства и признаки (с рисунками) одной из основных геометрических фигур – ромба.
- Определение ромба
- Свойства ромба
- Свойство 1
- Свойство 2
- Свойство 3
- Свойство 4
- Свойство 5
- Признаки ромба
- Ромб. Формулы, признаки и свойства ромба
- Признаки ромба
- Основные свойства ромба
- Сторона ромба
- Формулы определения длины стороны ромба:
- Диагонали ромба
- Формулы определения длины диагонали ромба:
- Периметр ромба
- Формула определения длины периметра ромба:
- Площадь ромба
- Формулы определения площади ромба:
- Окружность вписанная в ромб
- Формулы определения радиуса круга вписанного в ромб:
- Вписанная в ромб окружность
- 💥 Видео
Видео:Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать
Определение ромба
Ромб – это фигура на плоскости; разновидность параллелограмма, у которого все четыре стороны равны и попарно параллельны. Обычно ромб обозначается названиями его вершин (например, ABCD), а длина его стороны – строчной латинской буквой (например, a).
Примечание: квадрат является частным случаем ромба.
Видео:№700. Докажите, что в любой ромб можно вписать окружность.Скачать
Свойства ромба
Свойство 1
Противоположные углы ромба равны между собой, а сумма соседних углов составляет 180°.
Свойство 2
Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам.
В результате пересечения диагоналей ромб делится на 4 прямоугольных треугольника: ΔAEB, ΔBEC, ΔAED и ΔDEC.
Свойство 3
Диагонали ромба являются биссектрисами его углов.
Свойство 4
Сторону ромба a можно найти через его диагонали d1 и d2 (согласно теореме Пифагора).
- a – гипотенуза любого из 4 прямоугольных треугольников (например, ΔBEC );
- половины диагоналей d1 и d2 – катеты треугольников.
Свойство 5
В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Радиус вписанной в ромб окружности r вычисляется по формуле:
Видео:4K Как вписать окружность в ромб, видео 2023-2024 годСкачать
Признаки ромба
Параллелограмм является ромбом только в том случае, если для него верно одно из следующих утверждений:
- Его диагонали пересекаются под прямым углом.
- Если его диагонали являются биссектрисами его углов.
- Две смежные стороны равны (следовательно, все стороны равны).
Примечание: Любой четырехугольник, стороны которого равны, является ромбом.
Видео:Задача 6 №27914 ЕГЭ по математике. Урок 132Скачать
Ромб. Формулы, признаки и свойства ромба
 |  |
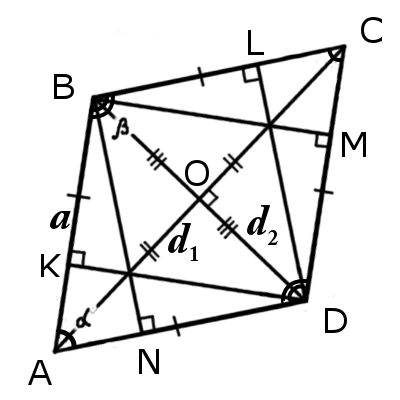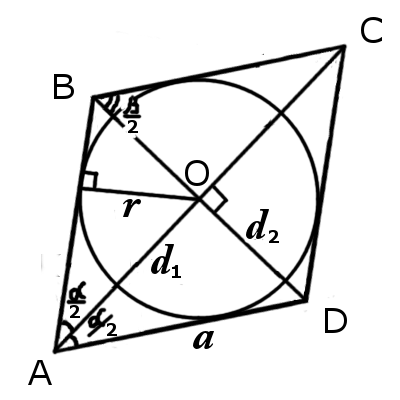| Рис.1 | Рис.2 |
Видео:Площадь ромба. Легче понять...Скачать
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Видео:ОКРУЖНОСТЬ (радиус окружности, вписанной в ромб) ЧАСТЬ 11Скачать
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
4. Формула стороны ромба через две диагонали:
| a = | √ d 1 2 + d 2 2 |
| 2 |
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
| a = | d 1 |
| √ 2 + 2 cosα |
| a = | d 2 |
| √ 2 — 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
8. Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Видео:Радиус вписанной в ромб окружности (6701)Скачать
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 — 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 — 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Видео:Задача 6 №27913 ЕГЭ по математике. Урок 131Скачать
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Видео:Геометрия 8 класс (Урок№6 - Прямоугольник. Ромб. Квадрат.)Скачать
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
| S = | 1 | d 1 d 2 |
| 2 |
5. Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4 r 2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Видео:Ромб и квадрат | Геометрия 7-9 класс #46 | ИнфоурокСкачать
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2 a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √ S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d 1 · d 2 |
| 4 a |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Видео:Окружность вписана в треугольник так,что образует у вершины ромбСкачать
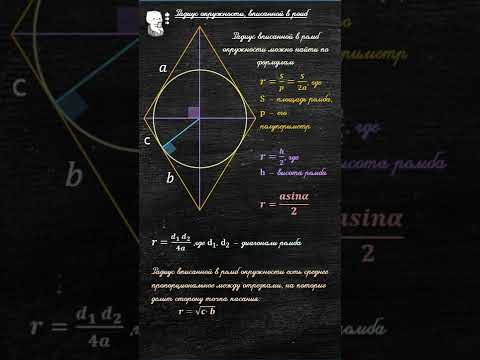
Вписанная в ромб окружность
Какими свойствами обладает вписанная в ромб окружность? Как найти её радиус?
Центр вписанной в ромб окружности — точка пересечения его диагоналей.
Радиус вписанной в ромб окружности можно найти по общей формуле
где S — площадь ромба, p — его полупериметр.
Так как полупериметр ромба равен p=2a, где a — сторона ромба, эту формулу можно записать как
С учётом формул для нахождения площади ромба:
где α — угол ромба (причем α может быть как острым, так и тупым).
где d1и d2 — диагонали ромба.
Таким образом, еще две формулы радиуса вписанной в ромб окружности:
Так как диаметр вписанной окружности равен высоте ромба, радиус равен половине высоты ромба:
Если известно, что точка касания вписанной окружности делит сторону ромба на отрезки, то радиус можно выразить через длины этих отрезков.
Так как диагонали ромба взаимно перпендикулярны и радиус, проведённый в точку касания, перпендикулярен стороне, то по свойству высоты прямоугольного треугольника из треугольника AOD имеем
Следовательно, радиус вписанной в ромб окружности есть среднее пропорциональное между отрезками, на которые делит сторону точка касания:
💥 Видео
В любой ромб можно вписать окружность. | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать
Вписанная и описанная окружность - от bezbotvyСкачать
Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать
Вписанные и описанные окружности. Вебинар | МатематикаСкачать
Геометрия Один из углов ромба равен 60, а большая диагональ равна 24 см. Найдите радиус окружностиСкачать
Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать
№696. Докажите, что если в параллелограмм можно вписать окружность, то этот параллелограмм — ромб.Скачать
Один отрезок - диагональ четырёхугольника, диаметр окружности, высота ромбаСкачать
