Разделы: Математика
На итоговых уроках по геометрии времени на то, чтобы прорешать задачи по всему курсу в целом практически не остается. А в КИМы ЕГЭ традиционно включаются задачи, решение которых требует знаний планиметрии по теме «Вписанные и описанные окружности». Поэтому предложенный материал поможет не только вспомнить данную тему, но и систематизировать ранее полученные знания по решению планиметрических задач на вписанные и описанные окружности, а также подготовиться к решению подобных задач в ЕГЭ. При этом предполагается, что ученик хотя бы на минимальном уровне владеет всем курсом школьной геометрии (планиметрии).
Первым и важнейшим этапом решения геометрической задачи является построение чертежа. Нельзя научиться решать достаточно содержательные задачи, не выработав прочных навыков по изготовлению «хороших» чертежей, не выработав привычки (даже рефлекса) – не начинать решать задачу, пока не сделан «большой и красивый» чертеж. В качестве основного метода решения геометрических задач выдвигается алгебраический метод с составлением последующего алгоритма. Ставя во главу угла алгебраический метод, необходимо предостеречь от чрезмерного увлечения алгеброй и счетом, не забывать о том, что речь идет все же о геометрических задачах, а поэтому, работая над задачей, следует искать геометрические особенности, учиться смотреть и видеть геометрию. Выделив два слагаемых, определяющих умение решать геометрические задачи, – чертеж плюс метод, добавим сюда третье – владение определенными теоремами и опорными задачами, известными геометрическими фактами.
I. Необходимые теоремы и опорные задачи для окружности, вписанной в треугольник и четырехугольник, и окружности, описанной около треугольника и четырехугольника. (Приложение 1)
II. Решение задач по готовым чертежам (удобно воспользоваться кодоскопом).
При этом ученики устно объясняют ход решения задач, формулируют теоремы и опорные задачи, применяемые при решении задач по готовым чертежам.
Готовый чертеж
Дано
Найти
Решение
Ответ
PABC = ?
AB = BC = 12
MC = CN = 7, AC = 14, AK = AN = 7,
PABC = 12 + 12 + 14 = 38
Ответ: PABC = 38
AB = 6,
АО =
PABC = ?
1)
 ,
, 
2) АВ = ВС,
 , т.к. ВО – биссектриса
, т.к. ВО – биссектриса 3)
 АВС – равносторонний, PABC = 6 • 3 = 18
АВС – равносторонний, PABC = 6 • 3 = 18 Ответ: PABC = 18
АВ = 3,
ВД = 4
1. Доказать: NM
 AD
AD 2. R = ?
 AN и AC
AN и AC  DN, т.е. AC и DB – высоты
DN, т.е. AC и DB – высоты  АND, тогда NK – высота, т.к. они пересекаются в одной точке.
АND, тогда NK – высота, т.к. они пересекаются в одной точке. Значит NM
 AD.
AD. 2. AD =
 = 5, R =
= 5, R = 
Ответ: R = 2,5
 АВС, R =
АВС, R =  = 1,5
= 1,5 Ответ: R = 1,5
ОК = 5
R = ?
 .
.  BKO – прямоугольный, ВК = AK = 12,
BKO – прямоугольный, ВК = AK = 12, КО = 5, ВО =
 = 13 = R
= 13 = R Ответ: R = 13
III. Решение задач.
1. Найти периметр прямоугольного треугольника, если радиус вписанной окружности 2 см, а гипотенуза 13 см.
 | Пусть AM = AN = x, тогда AC = x + 2, CB = 2 + 13 – x = 15 – x (x + 2) 2 + (15 – x) 2 = 169 x 2 – 13x + 30 = 0 x1 = 10, x2 = 3; AC = 6, CB = 12; P = 30 см Ответ: P = 30 см. |
2. Радиус вписанной в прямоугольный треугольник окружности 3 см, О – центр вписанной окружности, 

 | АО – биссектриса,  AKO – прямоугольный, AKO – прямоугольный, sin  = sin 30 о = = sin 30 о =  , АО = 6, , АО = 6, AN = AK =  = 3 = 3 , AC = 3 + 3 , AC = 3 + 3 , , tg 60 о =  , CB = , CB =  SABC =  = =  Ответ: S =  см2. см2. |
3. Периметр треугольника 84. Точка касания вписанной окружности делит одну из сторон на отрезки 12 и 14. Найти радиус вписанной окружности и площадь 
 | P = 84, KB = BN = 16, ON =  = =  = r = r AB = 28, BC = 30, AC = 26 По формуле Герона: SABC =  = 336 = 336 Ответ: r =  ; S = 336. ; S = 336. |
4. В равнобедренном треугольнике расстояние от центра вписанной окружности до вершины не равного угла 5 см. Большая сторона 10 см. Найти радиус вписанной окружности.
 | OB = 5,  , , OM = OB .  = =  , BH = 5 + r, , BH = 5 + r, AH = 2r,  AHB – прямоугольный, AHB – прямоугольный,  4r 2 = 100 – (5 + r) 2 , r 2 + 2r – 15 = 0, r1 = – 5, r2 = 3 Ответ: r = 3 см. |
5. Основание равнобедренного треугольника, вписанного в окружность радиуса 5 см, равно 6 см. Найти периметр треугольника.
 |  AHO – прямоугольный: OH = 4, BH = 4 + 5 =9, AHO – прямоугольный: OH = 4, BH = 4 + 5 =9, AB = BC =  = =  P =  Ответ: P =  см. см. |
6. Периметр треугольника АВС равен 72 см. AB = BC, AB:AC = 13:10. Найти радиус описанной около треугольника окружности.
 | AB + BC + AC = 72,  , ,  AC = 20, AB = BC =  = 26, BH = = 26, BH =  = 24 = 24 BN = NA = 13,   , R = , R =  Ответ: R =  см. см. |
7. Основание тупоугольного равнобедренного треугольника равно 24 см, а радиус описанной окружности 13 см. Найти боковую сторону треугольника.
 | OC = 13, AC = 24, HC = 12  HOC – прямоугольный, OH = HOC – прямоугольный, OH =  = 5 = 5 BH = BO – OH =13 – 5 = 8  BHC – прямоугольный, BC = BHC – прямоугольный, BC =  Ответ:  см. см. |
8. Окружность, диаметром которой служит АС треугольника АВС, проходит через точку пересечения медиан этого треугольника. Найти отношение длины стороны АС к длине проведенной к ней медианы.
 | AO = OC = R = OM, BM = 2R, BO = 3R,  Ответ:  . . |
9. Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
 | SABCD =  Т.к. окружность вписанная, то AB + CD = AD + BC = 20 h = 2r = 8,  , SABCD = 10 • 8 = 80 , SABCD = 10 • 8 = 80 Ответ: 80. |
10. Дан ромб ABCD. Окружность, описанная около треугольника ABD, пересекает большую диагональ ромба AC в точке E. Найдите CE, если AB = 
 |  AOB – прямоугольный: AO = AOB – прямоугольный: AO =  = 16 = 16 AD = 32 По теореме об отрезках пересекающихся хорд: BO • OD = AO • OE, 8 • 8 = 16 • OE, OE = 4, CE = 16 – 4 = 12 Ответ: 12. |
IV. Задачи для самостоятельного решения.
1. Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, а радиус описанной окружности равен 5 см. Найдите больший катет треугольника.
2. Около равнобедренного треугольника с основанием АС и углом при основании 75о описана окружность с центром О. Найдите ее радиус, если площадь треугольника ВОС равна 16.
3. Найдите радиус окружности, вписанной в остроугольный треугольник АВС, если высота BH равна 12 и известно, что 

4. Один из катетов прямоугольного треугольника равен 15, а проекция второго катета на гипотенузу равна 16. Найдите диаметр окружности, описанной около этого треугольника.
5. В равнобедренный треугольник АВС вписана окружность. Параллельно его основанию АС проведена касательная к окружности, пересекающая боковые стороны в точках D и E. Найдите радиус окружности, если DE = 8, AC = 18.
6. Около треугольника ABC описана окружность. Медиана треугольника AM продлена до пересечения с окружностью в точке K. Найдите сторону AC, если AM= 18, MK = 8, BK = 10.
7. Окружность, вписанная в равнобедренный треугольник, касается его боковых сторон в точках K и A. Точка K делит сторону этого треугольника на отрезки 15 и 10, считая от основания. Найдите длину отрезка KA.
8. Угол В треугольника АВС равен 60 о , радиус окружности, описанной около АВС, равен 2. Найти радиус окружности, проходящей через точки А и С и центр окружности, вписанной в АВС.
9. Стороны треугольника равны 5, 6 и 7. Найти отношение отрезков, на которые биссектриса большего угла этого треугольника разделена центром окружности, вписанной в треугольник.
10. Радиус окружности, вписанной в прямоугольный треугольник, равен полуразности его катетов. Найти отношение большего катета к меньшему.
Ответ: (
11. Диагонали четырехугольника ABCD, вписанного в окружность, пересекаются в точке М, прямые AB и CD пересекаются в точке N. Известно, что 



12. Высоты AH и BK остроугольного треугольника ABC пересекаются в точке M, 
13. Около окружности описана равнобочная трапеция с основаниями 5 и 3. Найти радиус окружности.
Ответ: (
14. В равнобедренный 
15. Дан прямоугольный треугольник ABC с прямым углом C. Через центр O вписанной в треугольник окружности проведен луч BO, пересекающий катет AC в точке M. Известно, что AM = 

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Решение №1128 Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р …
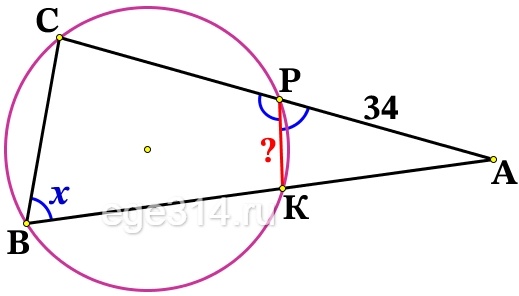
Окружность пересекает стороны АВ и АС треугольника АВС в точках К и Р соответственно и проходит через вершины В и С. Найдите длину отрезка КР, если АР = 34, а сторона ВС в 2 раза меньше стороны АВ.
Источник: ОГЭ 2021 Ященко (36 вар)
Четырёхугольник CBKP вписан в окружность, сумма противолежащих углов равна 180°. Пусть ∠В равен х , тогда противолежащий ∠СРК = 180° – х. Угол ∠АРК смежный к ∠СРК, тогда ∠АРК = 180 – (180 – х) = х. Значит ∠АРК = ∠В.
В ΔСАВ и ΔРАК: ∠АРК = ∠В, угол А общий, значит эти треугольники подобны по двум равным углам. Тогда и стороны подобны:
По условию АВ = 2·ВС , AP = 34 , тогда:
Ответ: 17.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Видео:Геометрия Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВССкачать

Решить задачу с треугольникам авс с пересекающей окружностью
Задание 16. В треугольнике ABC все стороны различны. Прямая, содержащая высоту ВН треугольника ABC, вторично пересекает описанную около этого треугольника окружность в точке F. Отрезок BD — диаметр этой окружности.
а) Докажите, что АВ = CF.
б) Найдите DF, если радиус описанной около треугольника ABC окружности равен 12, угол BAC = 35°, угол ACB = 65°.
а) Угол BCD – вписанный и опирается на диаметр окружности, значит, он равен 90°. Далее, пусть 





б) Угол 


Учитывая, что треугольник DBF прямоугольный с гипотенузой DB=2∙12=24 и углами 30° и 60°, катет DF, лежащий против угла в 30°, равен:
🌟 Видео
ОГЭ без рекламы математика 17 вариант задача 25Скачать

ОГЭ 2019. Задание 17. Разбор задач. Геометрия. Окружность.Скачать

ЕГЭ Задание 16 Описанная окружностьСкачать

Задание 24 ОГЭ по математике #3Скачать

Разбор Задачи №16 из работы Статград от 29 января 2020 (Запад)Скачать

ОГЭ. Задание 24. Геометрическая задача на вычисление.Скачать

Геометрия. ОГЭ по математике. Задание 15Скачать

Геометрия Окружность, построена на стороне AC треугольника ABC как на диаметре, пересекает сторонеСкачать

✓ Самая сложная задача в ОГЭ-2020 | Задание 26. Математика | Геометрия | Борис ТрушинСкачать

Геометрия Биссектрисы углов A, B и C треугольника ABC пересекают описанную около него окружностьСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

ОГЭ 2021. Задание 24. Геометрическая задача на вычисление.Скачать

Задание 24 ОГЭ по математике #7Скачать

Геометрия Биссектриса угла B треугольника ABC пересекает окружность, описанную около этогоСкачать

САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Геометрия. Задача. Треугольник. Окружность.Скачать
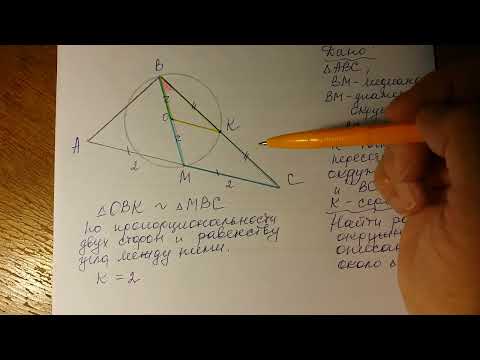
Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать