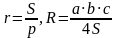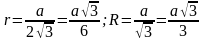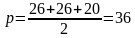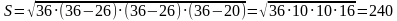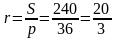Решение задач треугольников с вписанными и описанными окружностями

Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.

значит,

Приведем другое решение.

Высота правильного треугольника равна 3 радиусам вписанной окружности, поэтому она равна 18.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Окружность, описанная вокруг трапеции, описана и вокруг треугольника Это треугольник равнобедренный, угол при вершине равен 120°, углы при основании равны 30°. Найдем его боковую сторону:

откуда Тогда по теореме синусов:

Приведем другое решение (Р. А., СПб.).

Хорды AD, DC и CB равны, поэтому равны и стягиваемые ими дуги. Вписанный угол А равен 60°, он опирается на две из этих дуг и равен половине их суммы. Поэтому каждая из дуг равна 60°, их сумма равна 180°, а хорда АВ является диаметром. Отсюда получаем, что искомый радиус равен 6.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Решение задач по теме «Вписанная и описанная окружности»

Урок №7. СКАЧИВАЙТЕ файл на устройства, чтобы все знаки и формулы были видны и распознаны. Во время чтения файла онлайн происходит потеря формул.

Просмотр содержимого документа
«Решение задач по теме «Вписанная и описанная окружности»»

Тема: Решение задач по теме «Вписанная и описанная окружности»

Задачи: продолжить формирование навыков решения задач по теме.

Центр вписанной в треугольник окружности находится в точке пересечения его биссектрис.

Центр описанной около треугольника окружности находится в точке пересечения серединных перпендикуляров.

Формулы нахождения радиуса вписанной r и описанной R около треугольника окружностей.

Для любого треугольника:

Для равностороннего треугольника.

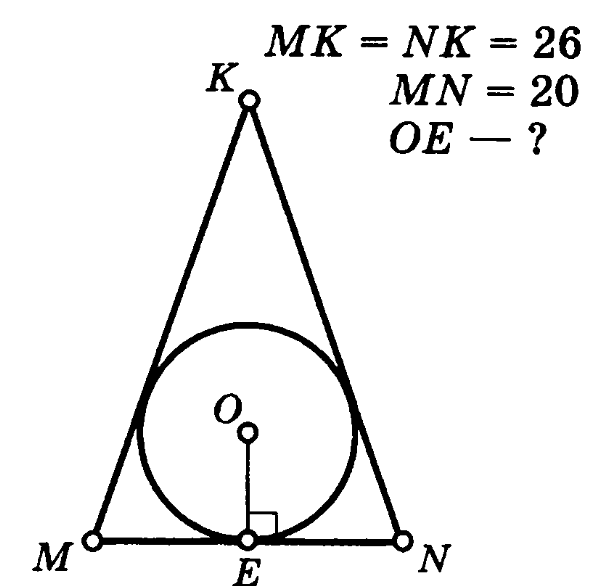
Задача 1. В равнобедренном треугольнике MKN боковые стороны равны 26, а основание – 20. В треугольник вписана окружность с радиусом ОЕ. Найти длину ОЕ.

Решение (краткое). Радиус окружности, вписанной в равнобедренный треугольник можно вычислить по стандартной формуле 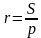, где р – полупериметр.

Ответ: .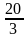

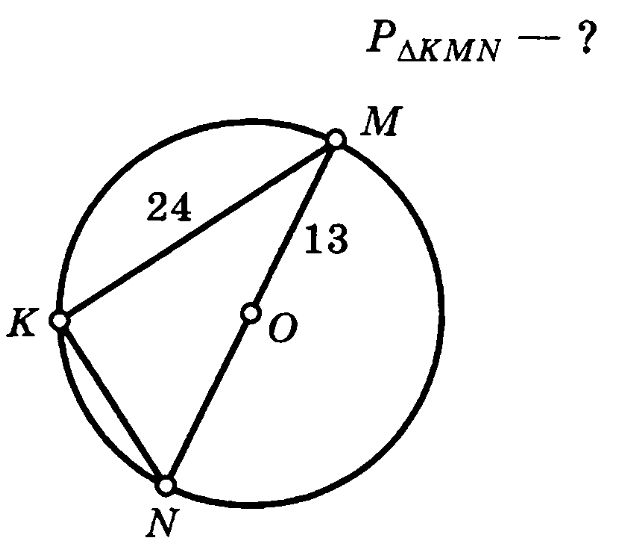
Задача 2. Прямоугольный треугольник KMN описан около окружности радиуса 13. Один из катетов треугольника равен 24. Найти периметр треугольника.

Решение (краткое). MN=d=2r=26, по теореме Пифагора KN=10, Р=60.

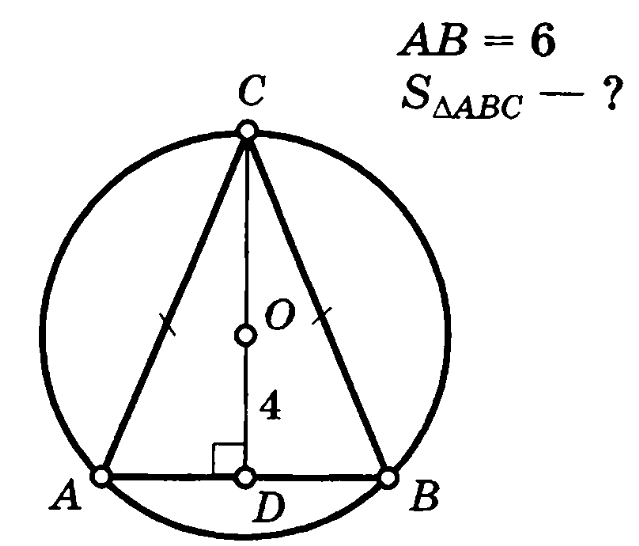
Задача 3. Равнобедренный треугольник АВС вписан в окружность, отрезок ОD=4. Найти площадь треугольника.

Решение (краткое). ОВ=5, ОС=ОВ=5, СD=9, S=0.5*9*6=27.

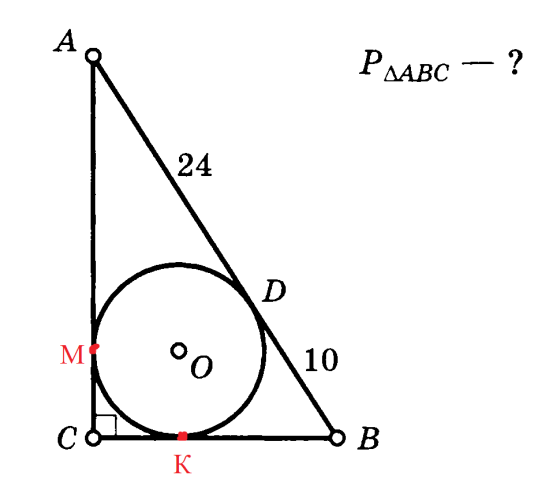
Задача 4. Прямоугольный треугольник описан около окружности. Точка D делит гипотенузу на две части, длинами по 10 и 24. Найти периметр треугольника.

Решение (краткое). DB=DK=10, AD=AM=24.

KOMC – квадрат, т.к. ОК перпендикулярен СВ, ОМ перпендикулярен АС и KC=CM, OK=OM=r.

Пусть KC=CM=х, тогда ВС=10+х, АС=24+х, АВ=24+10=34.

Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Классификация задач на вписанные в треугольник и описанные около треугольника окружности

Разделы: Математика

Задачи на вписанные в треугольник и описанные около треугольника окружности вызывают даже у сильных учащихся затруднения при их решении. Попытка провести классификацию этих задач по содержанию и методам решения привела к положительным результатам. Учащиеся полюбили этот тип задач. Хотим поделиться нашим опытом.

1. Замечательное открытие: люди изобрели колесо.
2. Окружность, описанная около треугольника.
3. Окружность, вписанная в треугольник.
4. Задачи на вписанные и описанные окружности.

На востоке от Аравийского полуострова с севера на юг текут две большие реки – Евфрат и Тигр. Между ними тянется узкая длинная полоса земли. В древности она называлась Месопотамией, что в переводе означает “ Междуречье’’. Самым известным государством Месопотамии был Вавилон. Земля в Междуречье плодородная, но там не было ни металлов, ни камня, ни леса, чтобы строить дома. Всё это вавилонянам приходилось покупать у других народов. Поэтому Вавилон раньше других стран стал вести большую торговлю. Торговля помогала науке. В математике вавилонские учёные добились больших успехов.

Около шести тысяч лет назад в Вавилоне было сделано замечательное открытие: люди изобрели колесо. Колесо? Что же тут замечательного? Но так кажется только на первый взгляд. Представьте себе на секунду, что вдруг случилось чудо, и на земле исчезли все колёса. Это было бы настоящей катастрофой! Остановятся автомобили и поезда, замрут заводы и фабрики, перестанут давать ток электростанции. Выходит, что неизвестный вавилонский изобретатель первого колеса действительно сделал великое открытие.

Вавилонские инженеры и мастера стали пользоваться блоками. Они поднимали и перетаскивали такие тяжести, справиться с которыми без колеса было бы не под силу. Колесо и рычаг стали первыми настоящими помощниками человека в работе с большими тяжестями.Так изобретение колеса сыграло очень большую роль в истории Вавилона.

Окружность называется описанной около многоугольника, если все вершины многоугольника лежат в окружности.

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Теорема. Около любого треугольника можно описать окружность.

Доказательство: Рассмотрим произвольный В треугольник АВС. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведём отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА=ОВ=ОС. Поэтому окружность с центром О радиуса ОА проходит через О все три вершины треугольника и, значит, является описанной около треугольника АВС.

Вывод: Центр описанной около треугольника окружности лежит А С на пересечении серединных перпендикуляров и расположен:

а) в треугольнике, если он остроугольный;

б) на середине гипотенузы, если он прямоугольный;

в) вне треугольника, если он тупоугольный.

Рассмотрим задачи на нахождение радиуса описанной около треугольника окружности. (См. Приложение1.)

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Теорема. В любой треугольник можно вписать окружность.

Доказательство: Рассмотрим произвольный треугольник АВС и обозначим М буквой О точку пересечения его биссектрис. Проведём из точки О перпендикуляры А К В ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА.

Так как точка О равноудалена A k B от сторон треугольника АВС то ОК = ОL=ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки К, L и М.

Стороны треугольника АВС касаются этой окружности в точках К, L и М, так как они перпендикулярны к радиусам ОК, ОL и ОМ.

Значит, окружность с центром О радиуса ОК является вписанной в треугольник АВС.

Выводы. Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис треугольника. Касательная к окружности (стороны треугольника) перпендикулярна к радиусу, проведённому в точку касания.

Рассмотрим задачи на нахождение радиуса вписанной в треугольник окружности.

Задачи на вписанную и описанную окружность. (См. Приложение 3.)

🎦 Видео

Всё про углы в окружности. Геометрия | МатематикаСкачать

Вписанная и описанная окружность - от bezbotvyСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Вписанная и описанная окружности. ЗадачиСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Вписанная и описанная окружности | Лайфхак для запоминанияСкачать

Описанная и вписанная окружности треугольника - 7 класс геометрияСкачать

Геометрия 8 класс. Тема: "Вписанная и описанная окружности. Решение задач"Скачать

Геометрия 9 класс. Вписанные и описанные окружности. Ключевая задача № 4.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Геометрия. 9 класс. Формулы для нахождения радиусов вписанной и описанной окружностей треугольникаСкачать

Тема 7. Вписанные и описанные окружности треугольникаСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Геометрия Найдите радиусы вписанной и описанной окружностей треугольника со сторонами 1) 5 см 5 смСкачать

Все о вписанных и описанных окружностях с нуля | PARTAСкачать

Геометрия 8 класс : Решение задач. Вписанная окружностьСкачать

Описанная и вписанная окружности четырехугольника - 8 класс геометрияСкачать

Решение задач на тему центральные и вписанные углы.Скачать