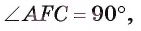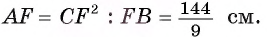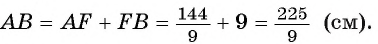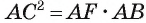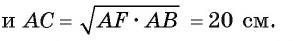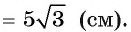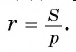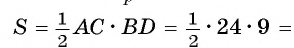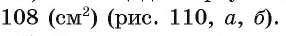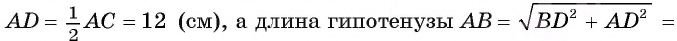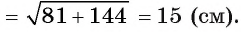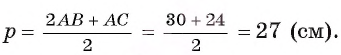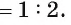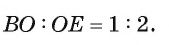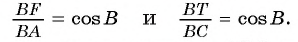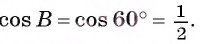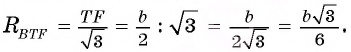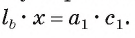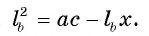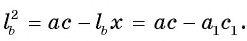Решение задач на вписанную окружность в треугольник с решением (8 видео)

Решение задач на вписанную окружность в треугольник с решением

Практикум по решению задач

§ 1. Использование формул планиметрии и тригонометрии

Решение наибольшего числа задач по планиметрии предполагает знание формул планиметрии и тригонометрии. Это прежде всего задачи на решение треугольников, нахождение различных линейных элементов в геометрических фигурах (длин медиан, биссектрис, радиусов окружностей и т. д.), определение углов.

1.1. Задачи на треугольник

При решении вычислительных задач на треугольник нужно знать следующие формулы (рис. 125):

где a, b, с – стороны треугольника;

?, ?, ? – противолежащие им углы;

r и R – радиусы вписанной и описанной окружностей;

ha, ma, la – высота, медиана и биссектриса, проведённые к стороне а;

S – площадь треугольника;

Иногда применяют формулу

а также формулу расстояния между центрами описанной и вписанной окружностей:

Примеры решения задач

1. Определите вид треугольника (остроугольный, тупоугольный или прямоугольный) со сторонами 8, 6 и 11 см (рис. 126). (1)

Решение. Обозначим больший угол треугольника через ?. Очевидно, что он лежит напротив стороны в 11 см, так как в треугольнике больший угол лежит против большей стороны. По теореме косинусов 112= 82+ 62– 2?8?6?cos ?;

cos ? = -7/32 ВС, то n > 1. Следовательно, уравнение (2) является квадратным. Его дискриминант равен (n + 1)2– 4(n – 1)2= – 3n2+ 10n – 3.

Уравнение (2) будет иметь решения, если – 3n2+ 10n – 3 ? 0, т. е. при -1/3 ? n ? 3. Т. к. n – натуральное число, большее 1, то уравнение (2) имеет решения при n = 2 и n = 3. При n = 3 уравнение (2) имеет корень х = 1; при n = 2 уравнение имеет корни

Ответ: отношение длины АВ к длине АС равно

при n = 2; равно 1 при n = 3; при остальных n решений нет.

Задачи для самостоятельного решения

10. В треугольнике ABC высота AD на 4 см меньше стороны ВС. Сторона АС равна 5 см. Найдите периметр треугольника ABC, если его площадь равна 16 см2. (1)

11. Докажите, что для любого треугольника выполняется равенство:

где ha, hb и hc – высоты треугольника, а r – радиус вписанной окружности. (2)

12. Основание треугольника равно ?2. Найдите длину отрезка прямой, параллельной основанию и делящей площадь треугольника пополам.(2)

13. Найдите площадь треугольника по стороне а и прилежащим к ней углам ? и ?. (2)

14. В треугольнике ABC длина высоты BD равна 6 см, длина медианы СЕ равна 5 см, расстояние от точки пересечения отрезков BD и СЕ до стороны АС равно 1 см. Найти длину стороны АВ. (3)

15. В треугольнике ABC высота BD равна 11,2, а высота АЕ равна 12. Точка Е лежит на стороне ВС, и BE: ЕС = 5:9. Найти длину стороны АС. (3)

16. В треугольнике ABC длина стороны АС равна 3, ?ВАС = ?/6 и радиус описанной окружности равен 2. Доказать, что площадь треугольника ABC меньше 3. (3)

17. В треугольнике ABC медианы, проведенные к сторонам АС и ВС, пересекаются под прямым углом. Длина стороны АС равна b, длина стороны ВС равна а. Найти длину стороны АВ. (3)

1.2. Задачи на равнобедренный и равносторонний треугольники

К задачам на равнобедренный треугольник применимы все формулы п. 1.1 этой главы, разве что во всех формулах b = с, ? = ?.

В случае равностороннего треугольника формулы значительно упрощаются, т. к. а = b = с, ? = ? = ? = 60°. Тогда

длины всех медиан, высот и биссектрис равны

Примеры решения задач

18. Один из углов равнобедренного треугольника равен 120°. Найдите отношение сторон треугольника (рис. 134). (1)

Решение. Обозначим основание треугольника через b, боковые стороны через а (см. рис.). По теореме косинусов

Тогда отношения сторон треугольника а: а: в = 1:1:?3.

19. Найдите площадь круга, описанного вокруг равностороннего треугольника со стороной а (рис. 135). (1)

Решение. Обозначим сторону треугольника через а. Тогда по теореме синусов имеем:

20. Основание равнобедренного треугольника равно 4?2, медиана боковой стороны равна 5. Найдите длину боковой стороны (рис. 136). (2)

Решение. Можно воспользоваться готовой формулой длины медианы:

Обозначим АВ через 2х, тотда ВМ = МС = х (см. рис.).

Задачу можно решить по-другому. Из ?ABC по теореме косинусов:

Далее, по той же теореме косинусов из ?АМВ:

21. На основании равнобедренного треугольника, равном 8 см, как на хорде, построена окружность, касающаяся боковых сторон треугольника. Найдите радиус окружности, если длина высоты, опущенной на основание треугольника, равна 3 см (рис. 137). (2)

Решение. Пусть данный треугольник ABC, где АВ = ВС; ВК = 3; АК = КС = 4 (см. рис.). Угол ОВС обозначим через ?. Из треугольника ВКС по теореме Пифагора находим:

Из того же треугольника следует: tg ? = 4/3. Радиус окружности R = ОС найдём из треугольника ВСО:

Задачи для самостоятельного решения

22. В равнобедренном треугольнике боковая сторона равна 12, а угол при вершине – 120°. Определите высоту треугольника. (1)

23. В равнобедренном треугольнике основание и опущенная на него высота равны 4. Найдите площадь описанного круга. (1)

24. В равнобедренном треугольнике высота равна 8, а основание относится к боковой стороне, как 6:5. Найдите радиус вписанной окружности. (1)

25. Длина окружности, описанной около равностороннего треугольника, равна 4. Найдите площадь заштрихованного сектора (рис. 138). (2)

26. Докажите, что сумма расстояний от любой точки равностороннего треугольника до его сторон равна длине высоты треугольника. (2)

1.3. Задачи на прямоугольный треугольник

Для прямоугольного треугольника с катетами а, b и гипотенузой с, помимо общих формул (см. п. 1.1 этой главы), характерны следующие соотношения:

(центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы); а = csin ? = ccos ? = btg? = bctg?.

Примеры решения задач

27. В прямоугольном треугольнике ABC, где угол АСВ = 90°, проведена высота CD. Известно, что угол СВА = 30°.

Найдите АВ/BD (рис. 139). (1)

Решение. Пусть АВ = а; тогда из ?ABC получаем: АС = a/2 (катет, лежащий напротив угла в 30°, равен половине гипотенузы). Далее, ?ACD = ?СВА = 30°, так как эти углы имеют взаимноперпендикулярные стороны. Из ?ACD следует:

28. Периметр прямоугольного треугольника равен 24 см, а его площадь равна 24 см2. Найдите площадь описанного около треугольника круга (рис. 140). (2)

Решение. Пусть а, b – длины катетов треугольников. Тогда длина гипотенузы равна

Периметр треугольника равен

а площадь 1/2 аb. Получаем систему уравнений:

Так как центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, то радиус окружности

29. На катете АС прямоугольного треугольника ABC как на диаметре построена окружность, которая пересекает гипотенузу АВ в точке К. Найти площадь треугольника СКВ, если длина катета AС равна b и величина угла ABC равна ? (рис. 141). (3)

Решение. Пусть ABC – данный в условии задачи треугольник. Так как АС – диаметр окружности, то угол СКА прямой и треугольник СКА прямоугольный. Поскольку величина угла САК равна 90° – ?, то величина угла КСА равна ?. Из прямоугольного треугольника СКА имеем, что СК = bcos ?. Из прямоугольного треугольника СКВ находим ВК = СК ctg? = bcos ? ctg?. Но тогда площадь треугольника СКВ равна

30. В треугольнике ABC угол А прямой, величина угла В равна 30°. В треугольник вписана окружность, радиус которой равен ?3. Найти расстояние от вершины С до точки N касания этой окружности с катетом АВ (рис. 142). (3)

Решение. Пусть ABC – прямоугольный треугольник, удовлетворяющий условию задачи. Обозначим через О центр окружности, вписанной в этот треугольник, а через M и N – точки касания этой окружности соответственно с катетами AС и АВ. Поскольку радиус, проведенный в точку касания, перпендикулярен касательной, то ОМ ? АС и ON ? АВ. Так как угол А прямой, то четырёхугольник AMON – прямоугольник. Отсюда следует, что AM = ON = ?3 и AN = OM = ?3. Рассмотрим треугольник ОМС. Это прямоугольный треугольник, у которого ?ОСМ = 1/2 (?АСВ) = ?/6. Так как ОМ = ?3 то МС = QM ? ctg ?/6 = 3. Но тогда AC = AM + МС = ?3 + 3. Из прямоугольного треугольника ANC находим, что

Задачи для самостоятельного решения

31. В прямоугольном равнобедренном треугольнике гипотенуза равна 12 см. Определите высоту треугольника, опущенную из прямого угла. (1)

32. В прямоугольном треугольнике ABC даны: длина катета ВС, равная 36, и косинус угла ВАС, равный 8/17. Найдите длину другого катета АС и площадь треугольника. (1)

33. Площадь равностороннего треугольника, построенного на гипотенузе прямоугольного треугольника, вдвое больше площади последнего. Определите углы прямоугольного треугольника. (2)

34. В прямоугольном треугольнике высота, опущенная из вершины прямого угла, делит гипотенузу на отрезки длиной 9 и 16. Найдите радиус вписанной в треугольник окружности. (2)

35. В треугольнике ABC угол ВАС прямой, длины сторон АВ и ВС равны соответственно 1 и 2. Биссектриса угла ABC пересекает сторону АС в точке L, G – точка пересечения медиан треугольника ABC. Что больше, длина BL или длина BG? (2)

36. На плоскости лежит равнобедренный прямоугольный треугольник, у которого катеты имеют длину. Поворотом в этой плоскости данного треугольника вокруг вершины его прямого угла на угол 45° получается другой равнобедренный прямоугольный треугольник. Найти площадь четырехугольника, являющегося общей частью этих двух треугольников. (3)

1.4. Задачи на трапецию

При решении задач на трапецию нужно помнить следующие положения:

где а, b – длины оснований, h – высота трапеции;

2) Если около трапеции ABCD можно описать окружность, то она равнобокая. Если при этом требуется найти радиус этой окружности, то он совпадает с радиусом окружности, описанной около любого из треугольников: ABC, ABD, ACD, BCD.

3) Если в трапецию ABCD вписана окружность, то AB + CD = BC + AD.

4) Трапецию принято изображать как на рис. 143.

При нижнем основании оба угла – острые, но она может выглядеть и как на рис. 144.

Поэтому, например, задача «Одно из оснований трапеции равно 6, боковые стороны трапеции равны ?5 и ?13. Высота трапеции равна 2. Найдите площадь трапеции» имеет 4 решения:16, 14, 10 и 8.

Примеры решения задач

37. В равнобокой трапеции ABCD высоты ВК и CL отсекают на основании AD отрезки АК и LD. Найдите длины этих отрезков, если AD = 19, ВС = 7 (рис. 145). (1)

Решение. Так как трапеция равнобокая, то треугольники АВК и CLD равны. В самом деле, АВ = CD по условию, ВК = CL как высоты трапеции. Значит, прямоугольные треугольники АВК и CLD равны по гипотенузе и катету. Так как KBCL – прямоугольник, то KL = ВС = 7; АК + LD = AD – KL = 19 – 7 = 12; AK = LD = 6.

38. Углы при основании трапеции равны 60° и 45°, высота трапеции равна 6 см. Найдите боковые стороны трапеции (рис. 146). (1)

Решение. Построим трапецию ABCD и проведём высоты ВК и СМ. Из прямоугольного ?АВК находим:

Из прямоугольного ?CMD получаем:

Ответ: 4?3 см; 6?2 см.

39. Средняя линия трапеции равна 10 и делит площадь трапеции в отношении 3:5. Найдите длины оснований этой трапеции. (2)

Решение. Рассмотрим трапеции EBCF и AEFD (рис. 147). Введем обозначения: AD = х, ВС = у; высоты трапеций EBCF и AEFD обозначим через h. Так как площадь трапеции равна произведению полусуммы оснований на высоту трапеции, то

Из свойства средней линии трапеции:

Таким образом, получаем систему уравнений:

40. В равнобедренной трапеции даны основания а = 21, b = 9 и высота h = 8. Найдите длину описанной около трапеции окружности (рис. 148; окружность на рисунке не показана). (2)

Решение. Проведём высоты трапеции ВК и СМ. Так как АВ = CD, то

Из ?АВК по теореме Пифагора получаем:

KD = KM + MD = 9 + 6 = 15. Так как окружность, описанная около трапеции, совпадает с окружностью, описанной около треугольника ABD, то по теореме синусов имеем:

41. В выпуклом четырёхугольнике MNLQ углы при вершинах N и L – прямые, а величина угла при вершине М равна arctg2/3. Найти длину диагонали NQ, если известно, что длина стороны LQ вдвое меньше длины стороны MN и на 2 м больше длины стороны LN (рис. 149). (2)

Решение: Из условия задачи следует, что угол NMQ острый. Пусть QK – высота треугольника MNQ. По условию LN ? MN и LN ? LQ, следовательно, MN||LQ и LN||QK, т. е. четырёхугольник KNLQ – параллелограмм. Тогда QK = LN и NK = LQ. Имеем, пользуясь условием задачи: QK = LN = LQ – 2, КМ = NM – NK = 2LQ – LQ = LQ. В прямоугольном треугольнике QKM отрезки QK и КМ являются катетами, следовательно,

и, значит, LQ – 2 = 2/3 LQ, откуда LQ = 6 и LN = 4. Из прямоугольного треугольника NLQ, наконец, по теореме Пифагора находим:

42. В трапеции ABCD отрезки АВ и DC являются основаниями. Диагонали трапеции пересекаются в точке Е. Найти площадь треугольника, ВСЕ, если АВ = 30 см, DC = 24 см, AD = 3 см и ?DAB = ?/3. (рис. 150). (3)

Решение. Обозначим через h длину высоты треугольника ABC, опущенной из вершины В на продолжение стороны АС. Так как этот отрезок одновременно является и высотой в треугольнике ВСЕ, то имеем:

Из полученных равенств находим:

В треугольниках ABE и CED равны величины соответствующих углов (?АЕВ = ?CED, ?ABE = ?CDE). Значит, эти треугольники подобны и

Теперь из (1) и (2) находим, что

Треугольники ABC и ABD имеют общее основание АВ. Поскольку АВ||CD, то их высоты, опущенные соответственно из вершин С и D, имеют равную величину. Поэтому

Задачи для самостоятельного решения

43. Найдите площадь равнобокой трапеции, если ее основания равны 12 и 4 см, а боковая сторона образует с одним из оснований угол в 45°. (1)

44. Меньшее основание равнобедренной трапеции равно высоте и равно h. Острый угол трапеции равен 30°. Найдите периметр трапеции. (1)

45. Длины параллельных сторон трапеции равны 25 и 4, а длины боковых сторон равны 20 и 13. Найдите высоту трапеции. (2)

46. Основания трапеции равны а и b, боковые стороны равны с. Найдите длину диагонали трапеции. (2)

47. Определите длину высоты трапеции, если её основания равны 28 и 16 см, а боковые стороны равны 25 и 17 см. (2)

48. Найдите площадь равнобедренной трапеции, у которой высота равна 10, а диагонали взаимно перпендикулярны. (2)

49. В трапецию ABCD с основаниями AD и ВС и с боковыми сторонами АВ и CD вписана окружность с центром О. Найти площадь трапеции, если угол DAB прямой, ОС = 2 и OD = 4. (3)

1.5. Задачи на параллелограмм

Площадь параллелограмма со сторонами а, b и углом ? между ними вычисляется по формуле S = absin ?. Можно также воспользоваться формулой S = 1/2 d1d2 sin? где d1, d2 – длины диагоналей, ? – угол между ними (или S = aha, где ha – высота). Если в параллелограмм можно вписать окружность, то это ромб. Если около параллелограмма можно описать окружность, то это прямоугольник.

Примеры решения задач

50. В параллелограмме сумма двух противолежащих углов равна 132°. Найдите градусную меру каждого из углов параллелограмма (рис. 151). (1)

Решение. По условию задачи ?А + ?С = 132°. Но, так как в параллелограмме противоположные углы равны, то ?А = ?С = 132°/2 = 66°. Учтём также, что ?А + ?В = ?С + ?D = 180°. Имеем:?В = ?D = 180° – 66° = 114°.

Ответ: 66°, 114°, 66°, 114°.

51. Одна из диагоналей параллелограмма разбивает его на два равносторонних треугольника со стороной а. Найдите длину другой диагонали (рис. 152). (1)

Решение. Раз ?ABD и ?BCD – равносторонние, то углы ?BAD = ?BCD = 60°, тогда ?ABC = 120°.

По теореме косинусов из треугольника ABC получаем:

52. Найдите площадь параллелограмма, если его диагонали 3 и 5, а острый угол параллелограмма 60° (рис. 153). (2)

Решение. Обозначим стороны параллелограмма: AD = а, АВ = b, ?BAD = 60°. BD = 3; АС = 5. Очевидно, что ?ABC = 120°. По теореме косинусов из треугольников ABD и АСВ имеем:

Вычитая первое уравнение из второго, получим 2ab = 16. Тогда площадь будет равна:

Задачи для самостоятельного решения

53. В параллелограмме с периметром 32 см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8 см. Найдите длины сторон параллелограмма. (1)

54. В параллелограмме ABCD длина диагонали BD, перпендикулярной стороне АВ, равна 6. Длина диагонали АС равна 2?22. Найдите длину стороны AD. (1)

55. Параллелограмм ABCD, у которого АВ = 153, AD = 180, BE = 135 (BE – высота), разделен на три одинаковые по площади фигуры прямыми, перпендикулярными AD. На каком расстоянии от точки А находятся точки пересечения этих перпендикуляров с AD? (2)

1.6. Задачи на ромб

Для ромба характерны все формулы для параллелограмма, только а = b.

Примеры решения задач

56. Тупой угол ромба в 5 раз больше его острого угла. Во сколько раз сторона ромба больше радиуса вписанной в него окружности (рис. 154)? (1)

Решение. Пусть сторона ромба равна а. В ромбе, как и во всяком параллелограмме, сумма внутренних односторонних углов BAD (обозначим этот угол ?А) и ABC (обозначим его ?В) равна 180°. Получаем систему уравнений:

Радиус r вписанной окружности, как видно из рисунка, равен половине высоты ВН ромба (2r = MN = ВН). Но из ?АВН следует, что

57. Высота ромба равна 12, а одна из его диагоналей равна 15. Найдите площадь ромба (рис. 155). (2)

Решение. Для нахождения площади ромба нам нужно знать длину стороны ромба и хотя бы один из его углов. Пусть АВ = а; ?А = ?. Проведём высоту ВН. Из ?АВН находим, что ВН = AB ? sin ?; 12 = asin ?. Из ?ABD по теореме косинусов BD2= АВ2+ AD2– 2AB ? AD ? cos ?; 152= а2 + а2– 2 ? a ? acos ?; 225 = 2а2(1 – cos ?). Получаем систему уравнений:

Делим первое уравнение на второе:

Задачи для самостоятельного решения

58. Диагональ ромба равна его стороне, ее длина 10 см. Найдите вторую диагональ и углы ромба. (1)

59. В ромб, сторона которого 20 см, вписан круг. Найти площадь круга, если одна диагональ ромба больше другой в 4/3 раза. (2)

60. В ромб с острым углом 30° вписан круг, площадь которого равна Q. Найдите площадь ромба. (2)

1.7. Задачи на прямоугольник

Для прямоугольника справедливы все формулы для параллелограмма, только угол между сторонами равен 90°. Поэтому S = ab = 1/2d2d2 sin?.

Примеры решения задач

61. Прямоугольник вписан в окружность радиуса 5 см. Одна из сторон равна 8 см. Найдите другие стороны прямоугольника (рис. 156). (1)

Решение. Очевидно, что центр описанной около прямоугольника окружности является точкой пересечения диагоналей прямоугольника. Из рисунка видно, что ОВ = 5, BE = BC/2 = 8/2 = 4.

Тогда по теореме Пифагора находим:

Ответ: 6 см; 8 см; 6 см.

62. Стороны прямоугольника 5 и 4 см. Биссектрисы углов, прилежащих к большей стороне, делят противолежащую сторону на 3 части. Найдите длины этих частей (рис. 157). (2)

Решение. Проведем в прямоугольнике ABCD биссектрисы AM и DK (см. рис. 157). Получим:?ВАМ = 1/2 ?BAD = 1/2 ?90° = 45°. Отсюда следует, что ?АВМ – равнобедренный (?ВMA = 45°) и, значит, ВМ = АВ = 4. МС = ВС – ВМ = 5–4 = 1.

Очевидно, что ВК = МС = 1;

КМ = ВС – ВК – МС = 5–1 – 1 = 3.

63. Из всех прямоугольников, вписанных в полукруг, найти прямоугольник наибольшей площади (рис. 158). (3)

Решение. Обозначив ?АОВ =?, получим: АВ = R sin ?, АО = R cos ?, S = AB ? AD = AB ? 2AO = 2R2sin ? ? cos ?, 0° ОС; значит, точка О лежит по одну сторону с точкой С относительно перпендикуляра к середине отрезка ВС. Отсюда следует, что точка О лежит на луче КС.

Обозначим КО через х и АВ = CD через y. Так как

Применяя к прямоугольному треугольнику KOD теорему Пифагора, получаем: OD2= КО2+ KD2или 169 = х2+ 1/2 у2.

Предположим, что КО ? КС или

тогда х2 ? 1/2 у2(заметим, что числа x и y неотрицательны) и

т. е. площадь квадрата не превосходит 169, что противоречит условию. Следовательно,

т. е. КО 0 и, значит, y = 17.

Ответ: длина стороны квадрата равна 17; точка О лежит внутри квадрата.

Задачи для самостоятельного решения

70. Сторона квадрата равна 7 см. Определите диаметр окружности, описанной около квадрата. (1)

71. В квадрат вписан круг, а в полученный круг вписан квадрат. Найдите отношение площадей квадратов. (1)

72. Квадрат со стороной 3 см срезан по углам так, что образовался правильный восьмиугольник. Найдите сторону восьмиугольника. (2)

73. Дан квадрат ABCD. На его сторонах вовне построены равносторонние треугольники ABM, BCN, CDK, DAL. Найдите площадь четырёхугольника MNKL, если АВ = 1. (2)

1.9. Задачи на n-угольник (n > 3)

Для произвольного выпуклого четырёхугольника S = 1/2 d1d2 sin?. Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны, a S = рr, где р – полупериметр, r – радиус вписанной окружности.

Если около четырёхугольника можно описать окружность, то суммы противоположных углов равны по 180°.

Для правильного n-угольника:

(R и r – радиусы описанной и вписанной окружностей, а – длина стороны правильного n-угольника).

Полезно также помнить, что в правильном шестиугольнике a6 = R.

Примеры решения задач

74. Сторона правильного шестиугольника равна 6. Найдите длину вписанной в него окружности (рис. 162). (1)

Решение. В правильном шестиугольнике сторона равна радиусу описанной окружности. Значит, треугольник АВО – правильный, угол АВО составляет 60°, a OB = R = 6. Радиусы вписанной в правильный шестиугольник окружности перпендикулярны его сторонам. В частности на рис. показано, что r ? АВ, где r = ОР. Тогда из прямоугольного треугольника ОРВ имеем:

75. Сколько сторон имеет выпуклый многоугольник, у которого все углы равны, если сумма его внешних углов с одним из внутренних равна 468°? (2)

Решение. Сумма внешних углов выпуклого многоугольника равна 360°, сумма внутренних углов равна 180°(n – 2). Величина угла в правильном n-угольнике равна

Задачи для самостоятельного решения

76. Сторона правильного шестиугольника равна 14. Найдите сторону равновеликого ему правильного треугольника. (1)

77. В правильный треугольник вписана окружность, а в неё – правильный шестиугольник. Найдите отношение площадей треугольника и шестиугольника. (2)

78. Выпуклый четырёхугольник ABCD описан вокруг окружности с центром в точке О, при этом АО = ОС = 1, ВО = OD = 2. Найти периметр четырёхугольника ABCD. (3)

1.10. Задачи на окружность и круг

При решении задач на окружность и круг применяются следующие формулы:

если ? выражена в радианах. Sсегмента = Sсектора – Sтреугольника.

Вписанный в окружность угол равен половине центрального угла, опирающегося на ту же дугу.

Примеры решения задач

79. Даны две концентрические окружности. Длина одной из них равна 33?, другой 27?. Найдите ширину кольца (рис. 163). (1)

Решение. Очевидно, что ширина кольца hкольца = R – r (см. рис). Зная длины окружностей, найдём их радиусы.

80. Найдите площадь сектора круга с радиусом R = 4 и центральным углом в 30°. (1)

Решение. Площадь сектора с углом в 30° в 36°/3° = 12 раз меньше площади всего круга. Значит, площадь сектора

81. Две окружности с радиусами R = 3 и r = 1 касаются внешним образом. Найдите расстояния от точки касания окружностей до их общих касательных (рис. 164, а; б). (2)

Решение. Из рисунка видно, что четырёхугольник АВ02О1 – трапеция. В самом деле, радиусы О1А и О2В перпендикулярны общей касательной АВ, а значит, параллельны друг другу. Проведём среднюю линию EF трапеции АВO2О1. По свойству средней линии трапеции находим

Легко видеть, что КМ – средняя линия трапеции EВО2F(см. рис. 164, б).

82. В сектор с центральным углом в 60° вписан круг. При каком радиусе сектора площадь круга равна ? (рис. 165)? (2)

Решение. Пусть АО = ОВ = ОС = х (см. рис). D – центр вписанного в сектор круга. Тогда ОС – биссектриса ?АОВ и ?СОВ = 1/2 ?АОВ = 1/2 ? 60° = 30°. Из прямоугольного треугольника ODK:

83. Диаметр окружности радиуса R является основанием правильного треугольника. Вычислите площадь той части треугольника, которая лежит вне данного круга (рис. 166). (2)

Решение. Как видно из рисунка, треугольники ADO и ОЕС – равносторонние (например, у ?ADO ?А = 60°; АО = OD, значит, ?ADO = 60°).

84. На плоскости даны две окружности с радиусами 12 см и 7 см и центрами в точках О1 и О2 касающиеся некоторой прямой в точках М1 и М2 и лежащие по одну сторону от этой прямой. Отношение длины отрезка М1М2 к длине отрезка О1O2 равно

Вычислить длину отрезка М1М2 (рис. 167). (3)

Решение. Пусть S1 и S2 – две окружности, удовлетворяющие условию задачи. Поскольку точки М1 и М2 являются точками касания окружностей S1 и S2 с прямой М1М2, то О1М1 ? М1М2 и O2М2 ? М1М2. Соединим центры О1 и O2 этих окружностей и проведём через точку О1 прямую, параллельную прямой М1М2. Пусть точка К будет точкой пересечения прямых O2М2 и прямой, проведённой параллельно прямой М1М2 через точку О1. Получим прямоугольный треугольник O1O2K с гипотенузой O1O2. Применяя к прямоугольному треугольнику О1КO2 теорему Пифагора, имеем:

О1О22= O1K2+ KO22(1)

Поскольку КМ2 = О1М1 и КO2 = КМ2 – М2O2, то КO2 = 5 см. Наконец,

Теперь из равенства (1) с учётом (2) и (3), а также КO2 = 5 см, следует, что 5/4 М1М22= М1М22+ 25, откуда

Задачи для самостоятельного решения

85. Дуги А1В1 и А2В2 равной длины 1 принадлежат разным окружностям с радиусами R1 и R2. Найдите отношение градусных мер центральных углов, соответствующих этим дугам. (1)

86. Точка лежит вне круга на расстоянии диаметра от центра круга. Найдите угол между касательными, проведенными из данной точки к данному кругу. (1)

87. В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найдите радиус окружностей. (2)

88. В равнобедренный треугольник, у которого боковая сторона равна 10 см, а основание 6 см, вписана окружность. Определите расстояние между точками касания, находящимися на боковых сторонах треугольника. (2)

89. Дано круговое кольцо, площадь которого Q. Определите длину хорды большего круга, касательной к меньшему. (2)

90. Круг радиуса

разделен на два сегмента хордой, равной стороне вписанного в этот круг правильного треугольника. Определите площадь меньшего из этих сегментов. (2)

91. Хорды АВ и АС имеют одинаковую длину. Величина образованного ими вписанного в окружность угла равна ?/6. Найти отношение площади той части круга, которая заключена в этом угле, к площади всего круга. (3)

§ 2. Основные идеи и методы решения планиметрических задач

Если в предыдущем параграфе мы рассматривали задачи, в которых центральное место принадлежит формулам планиметрии и тригонометрии, то теперь перейдем к задачам, где главную роль будут играть не формулы, а теоремы о свойствах и признаках геометрических фигур. Задачи в параграфе разбиты уже не по объекту исследования (треугольник, трапеция, круг и т. д.), а по ведущей идее решения.

2.1. Задачи на вписанную в треугольник окружность

Если в условии задачи говорится об описанной около треугольника окружности, то в большинстве случаев строить её не нужно. И наоборот, когда речь идёт о вписанной в треугольник окружности. Здесь не только нужно строить саму окружность, но и проводить радиусы к точкам касания (перпендикуляры к сторонам), а также соединять центр окружности с вершинами треугольника. При этом образуются равные треугольники.

Примеры решения задач

92. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 и 12 см. Найдите катеты треугольника (рис. 168). (1)

Решение. Впишем в треугольник ABC окружность и соединим её центр О с вершинами В, С. Проведём также перпендикуляры ОК, ON, ОМ (см. рис.). Они являются радиусами вписанной в треугольник окружности. Из равенства треугольников ВМО и BNO следует, что ВМ = BN = 5. Аналогично, из равенства треугольников ОКС и ONC следует, что КС = NC = 12. Заметим также, что AMOK– квадрат и, значит, AM = АК = r. Получаем, что АВ = АМ + МВ = r + 5, АС = АК + КС = r + 12. По теореме Пифагора получаем: АВ2+ АС2= ВС2.

(r + 5)2+ (r + 12)2= 172;

r2+ 10r + 25 + r2+ 24r + 144 = 289;

2r2+ 34r – 120 = 0;

r2+ 17r – 60 = 0; r = 3.

Катеты равны 5 + r = 8 и 12 + r = 15.

Ответ: 8 см; 15 см.

93. В треугольник вписана окружность с радиусом 4. Одна из сторон треугольника разделена точкой касания на отрезки, длины которых 6 и 8. Найдите длины сторон треугольника (рис. 169). (2)

Решение. Как и в предыдущей задаче, изобразим вписанную в треугольник окружность и соединим центр окружности О с вершинами треугольника. Проведем также перпендикуляры ОМ, ОТ, ОК, являющиеся радиусами окружности. Получены три пары равных треугольников: OAK и ОAT, ОВМ и ОВТ, ОСМ и ОСК. По условию одна из сторон треугольника разделена точкой касания на отрезки, длины которых 6 и 8. Пусть для определенности эта сторона – ВС и ВМ = 8, МС = 6. Тогда ВТ = ВМ = 8, СК = СМ = 6. Длины отрезков АК и AT обозначим через х. Для нахождения величины х воспользуемся формулой S = рг. По формуле Герона

Задачи для самостоятельного решения

94. Точка касания окружности, вписанной в равнобедренный треугольник, делит боковую сторону на отрезки в 3 и 4 см, считая от основания. Найдите периметр треугольника. (1)

95. Около окружности описана равнобокая трапеция, у которой боковая сторона точкой касания делится на отрезки 4 и 9 см. Найдите площадь трапеции. (2)

96. В прямоугольный треугольник, периметр которого равен 36 см, вписана окружность. Гипотенуза делится точкой касания в отношении 2:3. Найти длины сторон треугольника. (3)

2.2. Задачи на свойства параллельных прямых

В ряде задач используют свойства параллельных прямых: при пересечении двух параллельных прямых третьей образуются равные углы (рис. 170).

Квартеты равных углов:?1 = ?4 = ?6 = ?8; ?2 = ?3 = ?5 = ?7.

Особенно часто эти свойства применяются при решении задач на параллелограмм.

Примеры решения задач

97. В параллелограмме ABCD проведена биссектриса угла А, которая пересекает сторону ВС в точке F. Найдите длину BF, если сторона АВ = 11 (рас. 171). (1)

Решение. Из рисунка видно, что ?BFA = ?FAD (внутренние накрест лежащие при параллельных прямых), но ?BAF = ?FAD по условию, и поэтому ?BFA = ?BAF. Значит, треугольник ABF – равнобедренный, и BF = АВ = 11.

98. В параллелограмме ABCD сторона АВ равна 6 см, а высота, проведенная к основанию AD, равна 3 см. Биссектриса угла BAD пересекает сторону ВС в точке М так, что МС = 4 см. N – точка пересечения биссектрисы AM и диагонали BD. Вычислить площадь треугольника BNM (рис. 172). (3)

Решение. Пусть АВCD – данный в условии задачи параллелограмм. Проведем через точку N высоту параллелограмма QR. Обозначим через ? величину угла ВАМ; тогда величина угла АМВ равна ?, т. к. ВС||AD и AM – секущая. Следовательно, треугольник АВМ равнобедренный и ВМ = АВ = 6 см, откуда заключаем, что ВС = AD = ВМ + МС = 6 + 4 = 10 см. Поскольку ?ВМА = ?MAD и ?MBN = ?BDA, как накрест лежащие углы при параллельных ВС и AD, то треугольники BMN и AND подобны по двум углам. Так как в подобных треугольниках сходственные стороны пропорциональны сходственным высотам, то из подобия треугольников AND и BNM имеем:

откуда QN = 9/8 см.

Площадь треугольника BNM равна:

Задачи для самостоятельного решения

99. В параллелограмме ABCD угол BCD равен 60°, длина стороны АВ равна а. Биссектриса угла BCD пересекает сторону AD в точке N. Найдите площадь треугольника NCD. (1)

100. Периметр параллелограмма равен 90 см и острый угол содержит 60°. Диагональ параллелограмма делит его тупой угол в отношении 1:3. Найдите стороны параллелограмма. (1)

101. В параллелограмме ABCD биссектриса тупого угла В пересекает сторону AD в точке F. Найдите периметр параллелограмма, если АВ = 12 и AF: FD = 4:3. (1)

2.3. Задачи на пропорциональные отрезки

Теорема Фалеса (а также теоремы Чевы и Менелая) применяются в первую очередь тогда, когда в задаче даны соотношения между отрезками. Очень часто при этом приходится проводить дополнительный отрезок. Идеи использования теоремы Фалеса хорошо видны на следующих примерах.

Примеры решения задач

102. Докажите, что медианы в треугольнике делятся в отношении 2:1, считая от вершины (известная теорема школьного курса математики). (2)

Самый простой путь решения (рис. 173):

Проведем медианы AM и ВК, а также отрезок МТ, параллельный ВК. Имеем: т. к. ВМ = МС, то КТ = ТС. Но тогда АК = КС = 2КТ и, значит, АО: ОМ = АК: КТ = 2, что и требовалось доказать.

103. В треугольнике ABC на стороне ВС взята точка М так, что MB = МС, а на стороне АС взята точка К так, что АК = 3 ? КС. Отрезки ВК и АМ пересекаются в точке О. Найдите AO/OM (рис. 174). (2)

Решение. Обозначим длину отрезка КС через а, тогда АК = За. Проведём MP||ВК По теореме Фалеса КР = РС = a/2. По теореме о пропорциональных отрезках имеем:

104. В треугольнике ABC на стороне АВ взята точка К так, что АК: ВК = 1:2, а на стороне ВС взята точка L так, что CL: BL = 2:1. Пусть Q – точка пересечения прямых AL и СК. Найти площадь треугольника ABC, если дано, что площадь треугольника BQC равна 1 (рис. 175). (3)

Решение. Проведём через точку L прямую LM параллельно прямой СК. Из подобия треугольников MBL и КВС следует, что

Из подобия треугольников AKQ и AML находим:

Кроме того, имеем следующие равенства:

Задачи для самостоятельной работы

105. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC(рис. 176). (2)

106. На сторонах АВ и АС треугольника ABC взяты точки M и N, такие, что AM/MB = CN/NA = 1/2.

Отрезки BN и СМ пересекаются в точке К. Найти отношения отрезков BK/KN и CK/KM.(2)

2.4. Задачи на свойства биссектрисы треугольника

Биссектриса треугольника обладает одним замечательным свойством: она делит противолежащую сторону на отрезки, пропорциональные соответствующим боковым сторонам (рис. 177).

с/а = d/b или c/d = a/b.

Это свойство часто используется в задачах, в которых фигурирует биссектриса треугольника.

Примеры решения задач

107. В треугольнике ABC проведена биссектриса AD. Найдите периметр треугольника ABC, если АС = 4; DC = 2; BD = 3 (рис. 178). (1)

Решение. По свойству биссектрисы BD/AB = DC/AC; 3/AB = 2/4; АВ = 6.

Периметр треугольника РАВС = 6 + 5 + 4 = 15.

108. Дан треугольник ABC, в котором ?В = 30°, АВ = 4, ВС = 6. Биссектриса угла В пересекает сторону АС в точке D. Определите площадь треугольника ABD (рис. 179). (2)

Решение. По свойству биссектрисы AD/DC = AB/BC = 4/6 = 2/3.

Пусть AD = 2х; DC = Зх.

Задачи для самостоятельного решения

109. В треугольнике ABC, где АВ = 6, АС = 4, биссектриса AL и медиана ВМ пересекаются в точке О. Найдите BO/OM (1).

110. Определите стороны треугольника, если медиана и высота, проведённые из вершины одного угла, делят этот угол на три равные части, а сама медиана равна 10 см. (2)

2.5. Задачи на подобие

Два треугольника подобны: по двум углам, по двум сторонам и углу между ними, по трём сторонам. Очень важно в задаче увидеть подобные треугольники или другие подобные фигуры. Для этого нужна хорошая практика решения задач.

При решении задач на прямоугольный треугольник полезно знать, что высота, проведённая из прямого угла, делит его на два подобных треугольника (рис. 180):

Примеры решения задач

111. Через точки М и К, принадлежащие сторонам АВ и ВС треугольника ABC соответственно, проведена прямая МК, параллельная стороне АС. Найдите длину СК, если ВС = 12, МК = 8 и АС = 18 (рис. 181). (1)

Решение. Обозначим КС через х. Тогда ВК = 12 – х. Из подобия треугольников ABC и МВК следует: MK/BK = AC/BC; 8/(12 – x) = 18/12; x = 20/3.

112. В прямоугольный равнобедренный треугольник вписан прямоугольник так, что угол прямоугольника совпадает с углом при вершине треугольника, а вершина противолежащего угла лежит на гипотенузе. Докажите, что периметр прямоугольника есть величина постоянная для данного треугольника (рис. 182). (1)

Решение. Пусть АВ = АС = а, DE = х; AD = у. Тогда DB = а – у; FC = а – х. Треугольник DEB подобен треугольнику FСЕ, значит, DE/DB = FC/FE; x/(a – y) = (a – x)/y; ху2= а2– ау – ах + ху; х + у = а; РADEF = 2(х + у) = 2а, т. е. не зависит от х и у.

113. В прямоугольном треугольнике ABC угол А – прямой. Опущена высота AD, равная ?5. Найдите произведение BD ? DC (рис. 183). (1)

Решение. Треугольники ADB и ADC подобны (?BAD = ?ACD, ?ABD = ?DAC). Значит, BD/AD = AD/DC; BD ? DC = AD2= (?5)2= 5.

114. В треугольнике ABC проведены высоты AD и СЕ. Докажите, что треугольники ABC и DBE подобны. Чему равен коэффициент подобия (рис. 184)? (2)

Решение. Из прямоугольного треугольника ВСЕ: BE = ВС ? cos В. Из ?ABD: BD = АВ ? cos В. Значит, две стороны BD и BE треугольника BDE пропорциональны сторонам АВ и ВС треугольника ABC, а угол В (угол между пропорциональными сторонами) у треугольников общий. ?BDE

?ABC по двум сторонам и углу между ними.

Ответ: kподобия = cos B.

115. В равносторонний треугольник вписана окружность. Этой окружности и сторон треугольника касаются три малые окружности. Найдите сторону треугольника, если радиус малой окружности равен 1 (рис. 185). (2)

Решение. Так как в равностороннем треугольнике ABC угол ABC = 60°, то ?ОВМ = 30° (см. рис.). Из центров О и О1 проведем перпендикуляры ОМ и О1Т к стороне ВС. По условию О1Т и О1K равны 1. Длины отрезков ОМ и ОК обозначим через R. Из треугольника ВТО1 следует, что ВО1 = О1Т/sin 30° = 1/0,5 = 2. Треугольники ВТО1 и ВМО подобны по двум углам (?BTO1 = ?BMO = 90°; ?OBM – общий). Отсюда следует, что O1T/O1B = OM/OB;

Теперь мы знаем радиус вписанной в равносторонний треугольник окружности. Осталось найти длину его стороны. Из треугольника ВОМ следует ВМ = OM ? ctg ?ОВМ = 3?3. Тогда ВС = 2ВМ = 6?3.

116. Из одной точки к окружности проведены две касательные. Длина каждой касательной равна 12 см, а расстояние между точками касания 14,4 см. Определите радиус окружности (рис. 186). (2)

Решение. Пусть ОА и ОВ – касательные к окружности с центром С; А и В – точки касания. Тогда СВ ? ОВ, СА ? ОА. Кроме того, ОС ? АВ и делит эту сторону пополам. ОА = 12 см, AM = 1/2 АВ = 7,2 см.

?МОА = ?АОС (углы с взаимноперпендикулярными сторонами), значит, ?ОАС подобен ?ОАМ; тогда

117. Центр О окружности радиуса длиной 3 лежит на гипотенузе АС прямоугольного треугольника ABC. Катеты треугольника касаются окружности. Найти площадь треугольника ABC, если известно, что длина отрезка ОС равна 5 (рис. 187). (3)

Решение. Пусть ABC – данный в условии задачи треугольник. Обозначим через M и N точки касания окружности соответственно со сторонами АВ и ВС. Соединив эти точки с центром О окружности, получим квадрат MBNO, и поэтому BN = ОМ = 3. Треугольник ONC прямоугольный, в нём ОС = 5, ON = 3. Следовательно,

Но тогда ВС = NC + NB = 7. Треугольники ONC и ABC подобны, поэтому AB/ON = BC/NC; AB/3 = 7/4; отсюда получаем, что AB = (ON ? BC)/NC = (3 ? 7)/4 = 21/4. Теперь находим S – площадь прямоугольного треугольника ABC:

Задачи для самостоятельного решения

118. В равнобедренный треугольник вписан параллелограмм так, что угол параллелограмма совпадает с углом при вершине треугольника, а вершина противолежащего угла лежит на основании. Докажите, что периметр параллелограмма есть величина постоянная для данного треугольника. (1)

119. Из точки D, лежащей на катете АС прямоугольного треугольника ABC, на гипотенузу СВ опущен перпендикуляр DE. Найдите длину CD, если СВ = 15, АВ = 9, СЕ = 4. (1)

120. Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40 см. Найдите катеты треугольника. (1)

121. В параллелограмме ABCD проведена диагональ BD и отрезок AF (F ? ВС), пересекающий BD в точке О. Известно, что ВО = 6, OD = 18, FB = 4. Определите сторону параллелограмма AD. (1)

122. В острый угол, равный 60°, вписаны две окружности, извне касающиеся друг друга. Радиус меньшей окружности равен 1. Найдите радиус большей окружности. (1)

123. Найдите длину стороны квадрата, вписанного в равнобедренный треугольник с основанием а и боковой стороной b так, что две его вершины лежат на основании, а две другие вершины – на боковых сторонах. (2)

124. В параллелограмме ABCD точка М– середина стороны СВ, N – середина стороны CD. Докажите, что прямые AM и AN делят диагональ BD на три равные части. (2)

125. В трапеции, основания которой равны а и b, через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найдите длину отрезка этой прямой, отсекаемого боковыми сторонами трапеции. (2)

126. В остроугольном треугольнике ABC из вершин А и С на стороны ВС и АВ опущены высоты АР и CQ. Известно, что площадь треугольника ABC равна 18, площадь треугольника BPQ равна 2, а длина отрезка PQ равна 2?2. Вычислите радиус окружности, описанной около треугольника ABC. (3)

2.6. Задачи на вписанные и описанные четырёхугольники

Если в четырёхугольник можно вписать окружность, то суммы его противоположных сторон равны.

Если около четырёхугольника можно описать окружность, то суммы противоположных углов равны 180°.

Примеры решения задач

127. Известно, что в трапецию ABCD с основаниями AD и ВС можно вписать окружность и около неё можно описать окружность, EF – её средняя линия. Известно, что АВ + CD + EF = 18. Найдите периметр трапеции (рис. 188). (1)

Решение. Так как в трапецию можно вписать окружность, то

Поскольку около трапеции можно описать окружность, то АВ = CD. Пусть АВ = CD = а; тогда из (1) следует AD + ВС = 2а и

По условию АВ + CD + EF = 18; тогда с учетом (2) получаем: а + а + а = 18; а = 6. Периметр трапеции PABCD = АВ + CD + AD + BC = 2(АВ + CD) = 4а = 24.

128. Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой стороной, равной 17 см. Найдите основания трапеции (рис. 189). (2)

Решение. Очевидно, что высота трапеции равна диаметру окружности. Высота ВК = 15 см; из прямоугольного треугольника АВК

Пусть BС = х, тогда AD = 8 + х + 8 = х + 16. Так как в трапецию вписана окружность, то AD + ВС = АВ + CD; х + 16 + х = 17 + 17; х = 9 см; AD = 9 + 16 = 25 см.

Ответ: 9 см; 25 см.

Задачи для самостоятельного решения

129. Четырёхугольник ABCD описан около окружности с центром О. Найдите сумму углов АОВ и COD. (1)

130. Определите площадь круга, вписанного в прямоугольную трапецию с основаниями а и b. (2)

131. Длины боковых сторон трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит её на две части, отношение площадей которых равно 5/11. Найдите длины оснований трапеции. (3)

2.7. Задачи на вписанные углы

Вписанный в окружность угол равен половине центрального угла, опирающегося на ту же дугу.

Примеры решения задач

132. Найдите ?ТОК, если О – центр окружности и ?ТЕК = 120° (рис. 190).(1)

Решение. Так как вписанный угол ТЕК равен половине центрального угла, опирающегося на ту же дугу, то

133. Дан правильный 30-угольник А1А2 . А30 с центром О. Найдите угол между прямыми ОА3 и А1А4 (рис. 191). (2)

Решение. Так как многоугольник А1А2 . A30 – правильный, то ?А3ОА4 = 360°/30 = 12°. Далее, ?А3А1А4 = 1/2 ?А3ОА4 = 6° (вписанный угол, опирающийся на дугу А3А4). ?А1ОА3 = 2 ? 12° = 24°;

Требуемый нам угол х является внешним углом к треугольнику А3А1В. Так как внешний угол треугольника равен сумме внутренних углов, с ним не смежных, то х = 6° + 78° = 84°.

134. В окружность вписан четырёхугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке Е. Прямая, проходящая через точку Е и перпендикулярная к АВ, пересекает сторону CD в точке М. Доказать, что ЕМ – медиана треугольника CED, и найти её длину, если AD = 8 см, АВ = 4 см и ?CDB = ? (рис. 192). (3)

Решение. Обозначим через К точку пересечения прямых АВ и ЕМ. Поскольку углы CDB и CAB опираются на одну и ту же дугу ВС, то ?CAB = ?CDB = ?. Из равенств ?DCE + CDB = ?/2, ?КЕА + ?САВ = ?/2, следует, что ?DCE = ?КЕА = ?СЕМ. Но это означает, что треугольник СЕМ равнобедренный, т. е. СМ = ЕМ. Далее, ?MED = ?/2 – ?СЕМ = ?/2 – (?/2 – ?) = ?CDB.

Итак, треугольник EMD равнобедренный, или DM = ЕМ. Этим доказано, что СМ = DM или что ЕМ – медиана треугольника CED.

Из прямоугольного треугольника ABE находим

АЕ = АВ ? cos?ЕАВ = АВ ? cos?CAB = 4 ? cos ?.

Далее, из прямоугольного треугольника AED по теореме Пифагора получаем

Задачи для самостоятельного решения

135. Окружности с центрами О и О1 касаются внутренним образом. Найдите угол В (рис. 193). (1)

136. Точка находится внутри круга радиуса 6 и делит проходящую через неё хорду на отрезки длиной 5 и 4. Найдите расстояние от точки до окружности. (2)

137. а) Докажите, что

138. Диагональ BD четырёхугольника ABCD является диаметром окружности, описанной около этого четырёхугольника. Вычислить длину диагонали АС, если BD = 2, AB = 1, ?ABD:?DBC = 4:3. (3)

2.8. Задачи на пропорциональность отрезков хорд и секущих окружности

Напомним свойства хорд и секущих (рис. 196).

Для обоих случаев ОА ? ОВ = ОС ? OD.

В частности, если А совпадает с В (ОА – касательная), то ОА2= ОС ? OD.

Примеры решения задач

139. Дано (рис. 197):

ОА = 4, АВ = 3, CD = 2. Найдите ОС. (1)

Решение. Пусть ОС = х, тогда ОА ? ОВ = ОС ? OD; 4 ? 7 = х(х + 2);

140. Стороны прямоугольника равны а и b. На стороне а, как на диаметре, построена окружность. На какие отрезки окружность делит диагональ прямоугольника (рис. 198)? (2)

Решение. Из точки С проведена секущая СА и касательная CD к окружности. По известному свойству имеем: СР ? СА = CD 2;

Задача для самостоятельного решения

141. ОА – касательная; ОВ = 4; ВС = 3. Найдите длину ОА (рис. 199). (1)

2.9. Задачи на использование дополнительных построений, вспомогательных фигур и геометрических преобразований

Задачи с использованием геометрических преобразований, дополнительных построений и вспомогательных фигур достаточно редки в современных школьных учебниках, но именно в этих задачах, на наш взгляд, проявляется красота геометрии. Это не случайно, ведь благодаря проведенной «лишней» линии, осуществленному повороту, построению симметричной фигуры или вспомогательной окружности даже очень сложная задача может решиться «в одну строчку». За примерами далеко ходить не надо.

Примеры решения задач

142. Найдите длину окружности, описанной около трапеции, стороны которой равны а, а, а и 2а (рис. 200). (1)

Решение. Легко видеть, что трапецию ABCD можно достроить до правильного шестиугольника (см. рис.), но у правильного шестиугольника радиус описанной окружности равен стороне шестиугольника: Rокр = а. Длина окружности l = 2?Rокр = 2?а.

143. Основания трапеции равны 4 см и 9 см, а диагонали равны 5 см и 12 см. Найти площадь трапеции и угол между её диагоналями (рис. 201). (2)

Решение. Пусть ABCD – данная трапеция, CD = 4 см, АВ = 9 см, BD = 5 см и АС = 12 см. Чтобы известные элементы включить в один треугольник, перенесём диагональ BD на вектор DC в положение СВ’. Рассмотрим треугольник АСВ’. Так как ВВ’CD – параллелограмм, то В’С = 5 см, АВ’ = АВ + ВВ’ = АВ + CD = 13 см. Теперь известны все три стороны треугольника АВ’С. Так как АС2+ В’С2= (АВ’)2= 52+ 122= 132, то треугольник АВ’С – прямоугольный, причем ?АСВ’ = 90°. Отсюда непосредственно следует, что угол между диагоналями трапеции, равный углу АСВ’, составляет 90°. Площадь трапеции, как и всякого четырёхугольника, равна половине произведения диагоналей на синус угла между ними. Отсюда площадь равна 1/2AC ? BD ? sin 90° = 1/2 ? 12 ? 5 ? 1 = 30 см2.

Ответ: 30 см2, 90°.

144. Основание АВ трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали АС равна а, а длина боковой стороны ВС равна b. Найти площадь трапеции (рис. 202). (3)

Решение. Пусть АВ = 2с, тогда CD = AD = с. Продолжим боковые стороны ВС и AD до пересечения их в точке Е. Получим треугольник ВАЕ. Так как CD = 1/2АВ, то CD – средняя линия треугольника ABE. Отсюда получаем, что СЕ = ВС = b и DE = AD = с. Получилось, что АВ = АЕ. Следовательно, треугольник ВАЕ равнобедренный и АС – его медиана. Но в равнобедренном треугольнике медиана, проведённая к основанию, является высотой, поэтому площадь треугольника ВАЕ можно вычислить так:

Далее, т. к. треугольники DCE и ABE подобны с коэффициентом подобия k = 1/2, то площадь треугольника DCE равна 1/4 площади треугольника ABE (отношение площадей подобных треугольников равно квадрату коэффициента подобия). Площадь трапеции, таким образом, равна 3/4 площади треугольника ABE, то есть равна 3/4аb

145. Внутри равностороннего треугольника ABC дана точка М, такая, что АМ = 1, ВМ = ?3 и СМ = 2. Найти длину АВ (рис. 203). (3)

Решение. Повернём треугольник АСМ вокруг точки С на 60°. Тогда точка А перейдёт в точку В, точка М – в некоторую точку D, треугольник АСМ – в треугольник BCD. При этом CD = СМ и ?MCD = 60°, следовательно, треугольник CDM – равносторонний, а значит, и ?CDM = ?DMC = 60°. С помощью поворота получен вспомогательный треугольник BDM. Заметим, что BD = AM = 1, ВМ = ?3, DM = CM = 2. Значит, треугольник BDM прямоугольный (ведь BM2+ BD2= (?3)2+ 12= DM2), ?DBM = 90° и ?BMD = 30° (противолежащий катет BD равен половине гипотенузы MD). Далее вычислим угол ВМС. ?ВМС = ?BMD + ?DMC = 30° + 60° = 90°. Применив теорему Пифагора к треугольнику ВСМ, найдём, что

Задачи для самостоятельного решения

146. Доказать, что медиана треугольника меньше полусуммы заключающих ее сторон. (1)

147. Туристы находятся на острове «А». Им надо прибыть на остров «В», – при этом сначала побывав на обоих берегах реки. Каков будет их кратчайший маршрут (рис. 204)? (2)

148. Средняя линия трапеции равна 4; отрезок, соединяющий середины оснований, равен 1; углы при основании трапеции равны 40° и 50°. Найдите длины оснований трапеции. (3)

2.10. Задачи, решаемые координатным и векторным методами

Вообще говоря, в данном случае речь идет не о частных идеях решения определенного класса задач, а об универсальных методах решения самых разнообразных геометрических проблем.

Суть метода состоит в том, что для решения задач вводится система координат (прямоугольная или аффинная), пишутся необходимые уравнения прямых, других фигур, по известным формулам находятся длины и углы.

Примеры решения задач

149. Даны точки А(-2; 1); В(1; 5); С(3; -2); D(6; 2). Является ли четырёхугольник ABCD параллелограммом? Ответ: обоснуйте. (1)

Решение. АВ = (3; 4); CD = (3; 4). Противоположные стороны четырёхугольника, таким образом, равны и параллельны. Значит, ABCD – параллелограмм.

Ответ: ABCD – параллелограмм.

150. В треугольнике ABC точка М – точка пересечения медиан. Выразите вектор AM через вектора АВ и АС (рис. 205). (2)

Решение. Медианы точкой пересечения делятся в отношении 2:1, считая от вершины, поэтому

Задачу можно решить проще, если достроить треугольник ABC до параллелограмма ABDC, тогда AM = 2/3 АК, но АК = 1/2 AD = 1/2 (АВ + АС). Отсюда сразу получаем, что AM = 1/3(АВ + АС).

151. В прямоугольнике ABCD точки М и N – середины сторон АВ и ВС. Точка О – точка пересечения AN и DM. Найдите AO/ON (рис. 206). (2)

Решение. Решим задачу аналитическим путём. Пусть А(0; 0); D (a; 0); B(0; b), тогда M(0; b/2); N(a/2; b). Напишем уравнения прямых AN и MD.

Точка О будет иметь координаты:

152. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC (рис. 207). (3)

Решение. См. задачу 105 (с. 88). Тогда мы решили её, применив теорему о пропорциональных отрезках. Здесь мы применим векторный подход и метод неопределенных коэффициентов.

Пусть ВА = а, ВС = b, АО = х ? AM, КО = у ? КС, тогда АО + ОК = АК, х ? АМ + (-у ? КС) = -1/2а.

Так как AM = AB + ВМ = – ВА + 3/4ВС = – а + 3/4b и КС = KB + ВС = -1/2ВА + ВС = -1/2а + b, то с учётом этого получаем уравнение: хAM + (-уКС) = -1/2а или х(-а + 3/4b) – у(-1/2а + b) = -1/2а. Приравнивая к нулю коэффициенты при векторах а и b, стоящих в левой и правой частях уравнения, получим систему:

153. В выпуклом четырёхугольнике ABCD диагонали АС и BD пересекаются в точке F. Известно, что AF = CF = 2, BF = 1, DF = 4, ?BFC = ?/3.

Найти косинус угла между векторами АВ и DC (рис. 208). (3)

Пусть ? – искомый угол между векторами АВ и DC тогда

Пользуясь свойствами скалярного произведения векторов и условиями задачи, вычислим АВ, DC и АВ ? DC. Так как

Теперь получаем, что

Задачи для самостоятельного решения

154. Найдите геометрическое место точек, равноудалённых от данной прямой и данной точки. (2)

155. Продолжения сторон AD и ВС четырёхугольника ABCD пересекаются в точке Р. Точки М и N – середины сторон АВ и CD. Доказать, что если прямая MN проходит через точку Р, то ABCD – трапеция. (3)

156. Дан равнобедренный треугольник ABC, в котором проведены высота CD и перпендикуляр DE к боковой стороне ВС. Точка M – середина отрезка DE. Доказать, что отрезки АЕ и СМ перпендикулярны. (3)

157. Доказать, что для треугольника ABC и любой точки Р выполняется неравенство:

2.11. Разные задачи

158. Можно ли утверждать, что треугольники равны по двум сторонам и медиане, проведенной к одной из этих сторон? Ответ: обоснуйте (рис. 209). (1)

Решение. Рассмотрим треугольники ABC и А1В1C1. Пусть AB = A1B1, BC = B1C1,AM = A1M1 (см. рис). Так как ВС = В1С1, то ВМ = В1М1 ?АВМ = ?A1B1M1 (по трём сторонам), значит, ?В = ?B1. В этом случае ?ABC = ?A1B1C1 по двум сторонам и углу между ними.

159. Определите острые углы прямоугольного треугольника, если медиана, проведённая к его гипотенузе, делит прямой угол в отношении 2:1 (рис. 210). (1)

Решение. Нарисуем треугольник ABC, где ?ВАС = 3? = 90°. Медиана AD равна длинам BD и CD, так как D – середина гипотенузы, а, значит, является центром описанной около треугольника окружности. Пусть для определённости ?BAD = 2?, ?DAC =?. Очевидно, что 2? + ? = 90°, ? = 30°. Учитывая, что треугольники BDA и DAC – равнобедренные, получаем:?В = 2? = 60°, ?С = ? = 30°.

160. Дан произвольный четырёхугольник ABCD. Точки М, N, Р, Q – середины его сторон. Докажите, что MNPQ – параллелограмм (рис. 211). (1)

Решение. Из условия задачи и чертежа видно, что MN – средняя средняя линия ?ABC и QP средняя линия ?ACD. Поэтому MN = 1/2АС и MN||AC; QP = 1/2АС и QP||АС. В итоге получаем, что MN = QP и MN||QP. Поэтому, по признаку параллелограмма четырёхугольник MNPQ – параллелограмм.

161. Диагонали АС и BD трапеции ABCD пересекаются в точке О. Докажите, что треугольник АОВ и COD имеют одинаковые площади (рис. 212). (2)

Решение. Обозначим через h высоту трапеции. Запишем равенства:

162. Стороны треугольника образуют арифметическую прогрессию. Доказать, что радиус окружности, вписанной в треугольник, равен 1/3 высоты, проведённой к средней по величине стороне треугольника. (3)

Решение. Пусть стороны а, b, с треугольника ABC образуют арифметическую прогрессию с разностью d. Будем считать, что а ? b ? с. тогда a = b – d, c = b + d, периметр Р = 2р = 3b.

Воспользуемся формулой r = S/P, получим r = 2S/3b. А так как S = 1/2bhb, то r = 1/3hb.

Задачи для самостоятельного решения

163. Диагонали трапеции делят её среднюю линию на три равные части. Как относятся основания этой трапеции? (1)

164. Докажите, что середины сторон равнобокой трапеции являются вершинами ромба. (1)

165. В параллелограмме, смежные стороны которого не равны, проведены биссектрисы четырех углов. Докажите, что при их пересечении образуется прямоугольник. (2)

166. Площадь четырёхугольника равна S. Найдите площадь параллелограмма, стороны которого равны и параллельны диагоналям четырёхугольника. (2)

167. Докажите, что в параллелограмме ABCD расстояния от любой точки диагонали АС до прямых ВС и CD обратно пропорциональны длинам этих сторон. (2)

168. В выпуклом четырёхугольнике длины диагоналей равны одному и двум метрам. Найти площадь четырёхугольника, зная, что длины отрезков, соединяющих середины его противоположных сторон, равны. (1)

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Классификация задач на вписанные в треугольник и описанные около треугольника окружности

Разделы: Математика

Задачи на вписанные в треугольник и описанные около треугольника окружности вызывают даже у сильных учащихся затруднения при их решении. Попытка провести классификацию этих задач по содержанию и методам решения привела к положительным результатам. Учащиеся полюбили этот тип задач. Хотим поделиться нашим опытом.

Замечательное открытие: люди изобрели колесо.
Окружность, описанная около треугольника.
Окружность, вписанная в треугольник.
Задачи на вписанные и описанные окружности.

На востоке от Аравийского полуострова с севера на юг текут две большие реки – Евфрат и Тигр. Между ними тянется узкая длинная полоса земли. В древности она называлась Месопотамией, что в переводе означает “ Междуречье’’. Самым известным государством Месопотамии был Вавилон. Земля в Междуречье плодородная, но там не было ни металлов, ни камня, ни леса, чтобы строить дома. Всё это вавилонянам приходилось покупать у других народов. Поэтому Вавилон раньше других стран стал вести большую торговлю. Торговля помогала науке. В математике вавилонские учёные добились больших успехов.

Около шести тысяч лет назад в Вавилоне было сделано замечательное открытие: люди изобрели колесо. Колесо? Что же тут замечательного? Но так кажется только на первый взгляд. Представьте себе на секунду, что вдруг случилось чудо, и на земле исчезли все колёса. Это было бы настоящей катастрофой! Остановятся автомобили и поезда, замрут заводы и фабрики, перестанут давать ток электростанции. Выходит, что неизвестный вавилонский изобретатель первого колеса действительно сделал великое открытие.

Вавилонские инженеры и мастера стали пользоваться блоками. Они поднимали и перетаскивали такие тяжести, справиться с которыми без колеса было бы не под силу. Колесо и рычаг стали первыми настоящими помощниками человека в работе с большими тяжестями.Так изобретение колеса сыграло очень большую роль в истории Вавилона.

Окружность называется описанной около многоугольника, если все вершины многоугольника лежат в окружности.

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Теорема. Около любого треугольника можно описать окружность.

Доказательство: Рассмотрим произвольный В треугольник АВС. Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведём отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА=ОВ=ОС. Поэтому окружность с центром О радиуса ОА проходит через О все три вершины треугольника и, значит, является описанной около треугольника АВС.

Вывод: Центр описанной около треугольника окружности лежит А С на пересечении серединных перпендикуляров и расположен:

а) в треугольнике, если он остроугольный;

б) на середине гипотенузы, если он прямоугольный;

в) вне треугольника, если он тупоугольный.

Рассмотрим задачи на нахождение радиуса описанной около треугольника окружности. (См. Приложение1.)

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются окружности.

Теорема. В любой треугольник можно вписать окружность.

Доказательство: Рассмотрим произвольный треугольник АВС и обозначим М буквой О точку пересечения его биссектрис. Проведём из точки О перпендикуляры А К В ОК, ОL и ОМ соответственно к сторонам АВ, ВС и СА.

Так как точка О равноудалена A k B от сторон треугольника АВС то ОК = ОL=ОМ. Поэтому окружность с центром О радиуса ОК проходит через точки К, L и М.

Стороны треугольника АВС касаются этой окружности в точках К, L и М, так как они перпендикулярны к радиусам ОК, ОL и ОМ.

Значит, окружность с центром О радиуса ОК является вписанной в треугольник АВС.

Выводы. Центр вписанной в треугольник окружности лежит в точке пересечения биссектрис треугольника. Касательная к окружности (стороны треугольника) перпендикулярна к радиусу, проведённому в точку касания.

Рассмотрим задачи на нахождение радиуса вписанной в треугольник окружности.

Задачи на вписанную и описанную окружность. (См. Приложение 3.)

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Треугольники и окружность — задачи с примерами решения

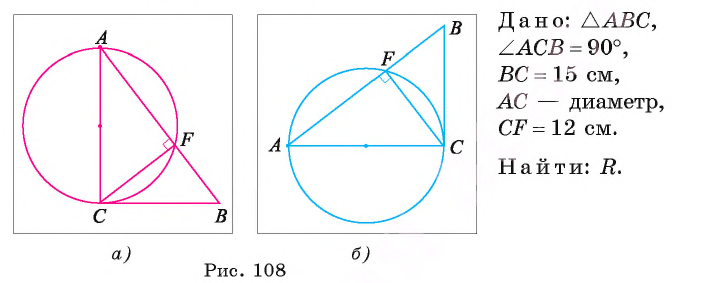
Пример:

Длина катета ВС прямоугольного треугольника АСВ равна 15 см, а его катет АС является диаметром окружности, которая пересекает гипотенузу в точке F, CF =12 см. Вычислите радиус окружности.

Решение:

Из условия следует, что радиус R равен половине катета АС. Заметим, что

1) В треугольнике

2) Воспользовавшись равенством 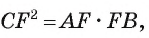найдем

3) Теперь

4) Квадрат длины катета прямоугольного треугольника равен произведению длины гипотенузы и длины проекции этого катета на гипотенузу, следовательно,

Таким образом,

Пример:

Решение:

По теореме об угле между хордой и касательной 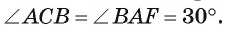Так как точки С и В диаметрально противоположные, то угол САВ опирается на диаметр, а следовательно, он прямой, т. е. треугольник САВ — прямоугольный (рис. 109, а, б). Расстояние от точки С до точки касания А равно длине катета СА треугольника САВ. Так как

Ответ

Пример:

Вычислите радиус окружности, вписанной в равнобедренный треугольник ABC, если длина его основания АС равна 24 см, а высота BD, проведенная к основанию, равна 9 см.

Решение:

Для вычисления радиуса г вписанной окружности воспользуемся формулой 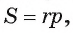где S — площадь треугольника, р — его полупериметр. Отсюда получим

1) Площадь треугольника

2) В прямоугольном треугольнике ADB длина катета

3) Теперь полупериметр

4) Таким образом, найдем

Пример:

В равнобедренном треугольнике ABC с основанием АС на стороне ВС лежит точка D так, что 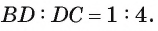В каком отношении точка О пересечения отрезка AD и высоты BE делит высоту BE, считая от вершины В?

Решение:

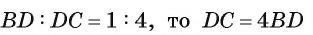
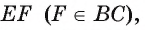
1) Так как (рис. 111, а, б). Проведем отрезок , параллельный отрезку AD.

2) Так как высота, проведенная к основанию равнобедренного треугольника, является медианой, то точка Е — середина стороны АС.

3) По признаку средней линии отрезок EF — средняя линия треугольника ADC, значит,

4) Так как

Ответ:

Пример:

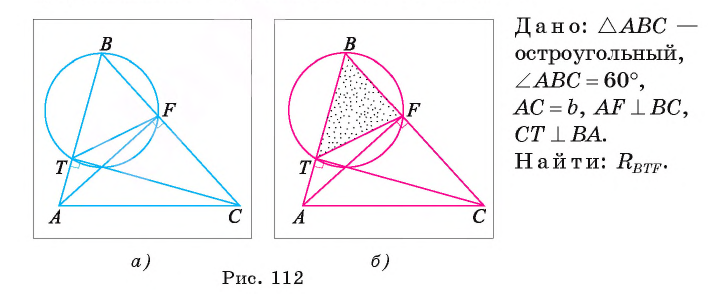
Отрезки AF и СТ — высоты остроугольного треугольника ABC. Найдите радиус окружности, описанной около треугольника BTF, если A ABC = 60° и АС = b.

Решение:

Воспользуемся теоремой синусов и тем, что треугольник ABC подобен треугольнику BTF.

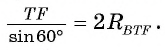
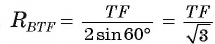
1) В треугольнике BTF по теореме синусов выполняется равенствоСледовательно, (рис. 112, a, 6).

2) Рассмотрим треугольники ABC и FTC. Эти треугольники подобны. Действительно,

Следовательно,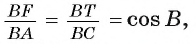т.е. треугольники подобны с коэффициентом подобия

3) Из подобия треугольников ABC и FTC следует, что 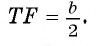Таким образом,

Ответ:

Пример:

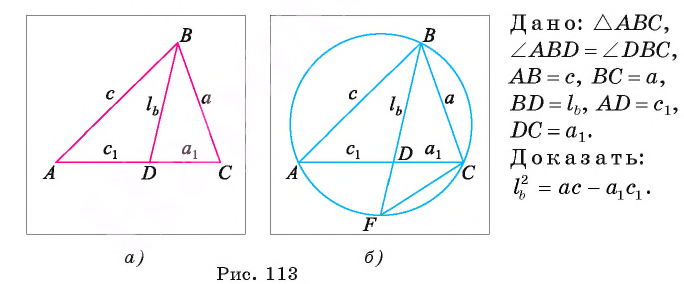
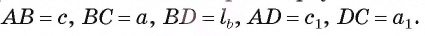
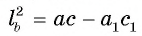
Отрезок BD — биссектриса треугольника ABC. Известно, что Докажите, что (рис. 113, а).

Рассмотрим окружность, описанную около треугольника ABC. Пусть прямая BD пересекает окружность в точке F и DF = х (рис. 113, б).

1) По свойству отрезков пересекающихся хорд выполняется равенство

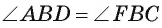
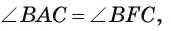
2) Треугольники ABD и FBC подобны, так как по условию и поскольку являются вписанными в окружность и опираются на одну и ту же дугу.

3) Из подобия треугольников ABD и FBC следует, что 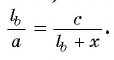Отсюда

3) Таким образом,

Что и требовалось доказать.

Рекомендую подробно изучить предметы:

Геометрия
Аналитическая геометрия
Начертательная геометрия

Ещё лекции с примерами решения и объяснением:

Площадь треугольника
Соотношения между сторонами и углами произвольного треугольника
Окружность и круг
Описанные и вписанные окружности
Пространственные фигуры — виды, изображения, свойства
Взаимное расположения прямых на плоскости
Треугольник
Решение треугольников

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.