Решение задач на тему хорды окружности (3 видео)

Задачи по теме Свойства хорд, касательных и секущих к окружности. Геометрия, 8 класс.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Содержание

«Снятие эмоционального напряжения у детей и подростков с помощью арт-практик и психологических упражнений»
Решение задач на тему хорды окружности
Определение хорды
Свойства хорды к окружности
Свойства хорды и вписанного угла
Свойства хорды и центрального угла
Формулы нахождения хорды
Решение задач
Математика. Задачи. Хорды, касательные и секущие.
💡 Видео

Видео:Это Свойство Поможет Решить Задачи по Геометрии — Хорда, Окружность, Секущая (Геометрия)Скачать

«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»

Сертификат и скидка на обучение каждому участнику

Задачи по геометрии 8 класс. Касательные, отрезки пересекающихся хорд и отрезки секущих к окружности.

Свойство пересекающихся хорд: произведение

отрезков одной хорды равно произведению

отрезков другой хорды

Хорды окружности АВ и СР пересекаются в точке Е. Найти длину отрезка РЕ, если СЕ= 8см, АЕ = 3 см, ВЕ = 6 см.

Хорды окружности АК и МЕ пересекаются в точке О. Найти длину отрезка МО, если АО= 4см, ОЕ = 5 см, ОК = 15 см.

Хорды окружности АК и МЕ пересекаются в точке О. Найти длину отрезка МО и ОЕ, если АО = 2 см, ОК = 12 см, МЕ = 10 см.

Хорды окружности АВ и СР пересекаются в точке Е. Найти длину отрезка РЕ и СЕ, если СР = 12 см, АЕ=7 см, ЕВ = 4 см.

Хорды окружности АВ и СД пересекаются в точке О. Найти длину отрезка ДО и ОС, если АО = 12 см, ОВ=4 см, ДО : ОС = 3 : 4.

Хорды окружности МК и СД пересекаются в точке А. Найти длину отрезка ДО и ОС, если МА = 6 см, АК=15 см, СА : АД = 2 : 5.

Свойство секущих к окружности, исходящих из

Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АС и ВС, если АМ = 3, МК = 5, АВ = 4.

Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и МК, если АВ = 4, ВС = 6, АК = 12.

Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АВ и АС, если АМ = 2, АК = 6, длина отрезка АС на 4 больше длины отрезка АВ.

Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и АК, если АВ = 2, АС = 8, длина отрезка АМ на 6 меньше длины отрезка АК.

Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АВ и ВС, если АМ = 4, АК = 6, АВ : ВС = 2 :4.

Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и АК, если АМ : АК = 3 : 5, АВ = 5, ВС = 7.

Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АВ и АС, если АМ = 2, АК = 4, длина отрезка ВС на 6 больше длины отрезка АВ.

Из точки А, лежащей вне окружности проведены лучи АС и АК, пресекающие окружность в точках В, С и М, К соответственно, начиная от точки А. Найти длину отрезка АМ и МК, если АМ на 8 меньше длины отрезка МК и длина отрезка АВ = 3, АС = 8.

Свойство секущей и касательной к окружности,

исходящих из одной точки:

Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АВ, если АК = 4, АР = 9.

Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АВ, если АК = 4, АР = 16.

Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР, если АК = 4, АВ = 8.

Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР, если АК = 5, АВ = 10.

Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АК и АР, если АВ = 5, а отрезок КР на 5 больше отрезка АК.

Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АК и АР, если АВ = 6, а отрезок КР на 6 больше отрезка АК.

Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР и АК, если АК : КР = 4 : 5, АВ = 12.

Из точки А, не лежащей на окружности проведена касательная АВ и секущая АК, которая пересекает окружность в точках К и Р начиная от точки А. Найти длину отрезка АР и АК, если АК : КР = 1 : 3, АВ = 14.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Решение задач на тему хорды окружности

Учебный курс

Решаем задачи по геометрии

Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Определение хорды

Хорда — это отрезок, который соединяет две точки заданной кривой. Хорда может быть у дуги, окружности, эллипса и т.д.
На рисунке хорда обозначена как отрезок AB красного цвета . Оба его конца находятся на окружности

Часть кривой, заключенной между двумя точками хорды, называется дугой.
На рисунке дуга хорды AB обозначена зеленым цветом .

Плоская фигура, заключенная между дугой и ее хордой называется сегментом.
Сегмент на рисунке ограничен красным отрезком AB с одной стороны, и зеленой дугой — с другой стороны.

Хорда, проходящая через центр окружности, называется диаметром окружности. Диаметр окружности — самая длинная хорда окружности.

Видео:Окружность. 7 класс.Скачать

Свойства хорды к окружности

Если расстояния от центра окружности до хорд равны, то эти хорды равны. Верно и обратное — если хорды равны, то расстояния от центра окружности до этих хорд равны
Если хорда больше, то расстояние от центра окружности до этой хорды меньше. Если хорда меньше, то расстояние от центра окружности до этой хорды больше. Верно и обратное
Наибольшая возможная хорда является диаметром
Серединный перпендикуляр к хорде проходит через центр окружности

Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр перпендикулярен этой хорде. Верно и обратное — если диаметр перпендикулярен хорде, то этот диаметр делит эту хорду пополам
Если диаметр делит хорду, не являющуюся диаметром, пополам, то этот диаметр делит дуги, стягиваемые этой хордой, пополам. Верно и обратное — если диаметр делит дугу пополам, то этот диаметр делит пополам хорду, стягивающую эту дугу

Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус перпендикулярен этой хорде. Верно и обратное — если радиус перпендикулярен хорде, то этот радиус делит эту хорду пополам
Если радиус делит хорду, не являющуюся диаметром, пополам, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус делит пополам хорду, стягивающую эту дугу.
Если радиус перпендикулярен хорде, то этот радиус делит дугу, стягиваемую этой хордой, пополам. Верно и обратное — если радиус делит дугу пополам, то этот радиус перпендикулярен хорде, стягивающей эту дугу.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Свойства хорды и вписанного угла

Видео:Геометрия 7 класс (Урок№16 - Окружность. Задачи на построение.)Скачать

Свойства хорды и центрального угла

Видео:Длина хорды окружности равна 72 ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Формулы нахождения хорды

Обозначения в формулах:
l — длина хорды
α — величина центрального угла
R — радиус окружности
d — длина перпендикуляра, проведенного от центра окружности к хорде

Длина хорды окружности равна удвоенному радиусу данной окружности, умноженному на синус половины центрального угла.
Сумма квадрата половины длины хорды и квадрата перпендикуляра, проведенного к этой хорде, равна квадрату радиуса окружности. Данная формула следует из теоремы Пифагора.

Видео:Геометрия 8 класс (Урок№28 - Свойства хорд окружности.)Скачать

Решение задач

Примечание. Если Вы не нашли решение подходящей задачи, пишите об этом в форуме. Наверняка, курс геометрии будет дополнен.

Задача.

Хорды АВ и СD пересекаются в точке S, при чем AS:SB = 2:3, DS = 12см, SC = 5см, найти АВ.

Решение.

Поскольку соотношение AS:SB = 2:3 , то пусть длина AS = 2x, SB = 3x

Согласно свойству хорд AS x SB = CS x SD, тогда

2х * 3х = 5 * 12
6х 2 = 60
х 2 = 10
x = √10

Откуда
AB = AS + SB
AB = 2√10 + 3√10= 5√10

Окружность разделена на части, которые относятся как 3,5:5,5:3 и точки деления соединены между собой. Определить величину углов образовавшегося треугольника.

Решение.
Обозначим коэффициент пропорциональности дуг окружности, как х. Соединим центры окружности с концами дуг. Поскольку центральный угол равен градусной мере дуги, на которую опирается, то соотношение центральных углов окружности будет равно соотношению ее частей (дуг).
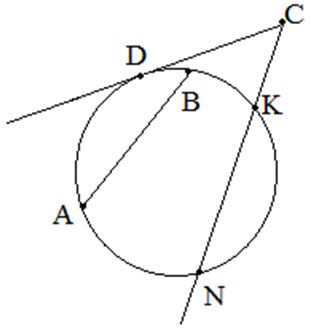
Поскольку градусная мера окружности равна 360 градусам, то

3,5х + 5,5х + 3х = 360
12х = 360
х = 30

Откуда градусные величины центральных углов равны:
3 * 30 = 90
3,5 *30 = 105
5,5 *30 = 165

Углы образовавшегося треугольника являются углами, вписанными в окружность. Вписанный угол равен половине градусной меры дуги, на которую опирается.
Откуда углы треугольника равны:

90 / 2 = 45
105 / 2 = 52,5
165 / 2 = 82,5

Ответ: Величина углов треугольника равна 45 ; 52,5 ; 82,5 ;

Видео:Теорема об отрезках хорд и секущихСкачать

Математика. Задачи. Хорды, касательные и секущие.

Хорды, касательные и секущие.

Окружностью называется геометрическое место точек, равноудаленных от одной точки, которая называется центром окружности.

Отрезок, соединяющий две точки окружности, называется хордой (на рисунке это отрезок ). Хорда, проходящая через центр окружности, называется диаметром окружности.

Хорда окружности обладает следующими свойствами:

Хорды, находящиеся на одинаковом расстоянии от центра окружности, равны.
Если хорды стягивают равные центральные углы, то они равны.
Если диаметр перпендикулярен хорде, то он проходит через ее середину.
Если вписанные углы опираются на одну хорду, то они равны.
Две дуги равны, если они заключены между двумя равными хордами.
Если пара вписанных углов опирается на одну и ту же хорду, а их вершины лежат по разные стороны хорды, то их сумма составляет 180°.
Для любых двух хорд и , пересекающихся в точке О, выполняется равенство: .

Прямая, имеющая с окружностью одну общую точку, называется касательной (на рисунке отрезок ).

Прямая, имеющая с окружностью две общие точки, называется секущей (отрезок ).

Свойства касательной и секущей

Касательная перпендикулярна радиусу, проведенному в точку касания.
Отрезки касательных, проведенных из одной точки, равны.
Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть: