Решение тригонометрических неравенств при помощи окружности (6 видео)

Решение тригонометрических неравенств с помощью единичной окружности

ГБОУ СОШ № 000 с углубленным изучением английского языка Адмиралтейского района Санкт-Петербурга

Решение тригонометрических неравенств с помощью единичной окружности

Тригонометрические неравенства одна из самых сложных тем в школьном курсе математики. При решении простейших тригонометрических неравенств удобно использовать тригонометрическую окружность для того, чтобы наиболее наглядно представить решения неравенства и верно записать множества решений данного неравенства.

Цель данной разработки — сформировать у школьников умения использовать тригонометрический круг при решении простейших неравенств вида sin x > a, sin x a, cosx , называются тригонометрическими неравенствами.

Решить тригонометрическое неравенство — это значит, найти множество значений неизвестных, входящих в неравенство, при которых неравенство выполняется.

Тригонометрические неравенства можно решать с помощью графиков функций y = sin x, y = cos x, y = tg x, y= ctg x или с помощью единичной окружности.

Решение тригонометрических неравенств, сводится, как правило, к решению простейших неравенств вида: sin x>a, sin xa, sin xa, sin x

Алгоритм решения тригонометрических неравенств

с помощью единичной окружности.

1) На оси ординат (абсцисс) отметить точку a и провести прямую y = a (x = a), перпендикулярную соответствующей оси.

2) Отметить на окружности дугу, состоящую из точек окружности, удовлетворяющих данному неравенству (эти точки расположены по одну сторону от построенной прямой).

3) Записать числовой промежуток, точки которого заполняют отмеченную дугу, и к обеим частям неравенства прибавить период функции ( для y = sin x и y = cos x ).

Решение простейших неравенств вида sin x>a, sin xa, sin xa, sin x

На единичной окружности проводим прямую y = , которая пересекает окружность в точках A и B.

Все значения y на промежутке NM больше , все точки дуги AMB удовлетворяют данному неравенству. При всех углах поворота, больших , но меньших , sin x будет принимать значения больше (но не больше единицы).

Таким образом, решением неравенства будут все значения на интервале , т. е. a, cos xa, cos xa, cos x

Содержание

Простейшие тригонометрические неравенства
п.1. Решение неравенств с синусом
п.2. Решение неравенств с косинусом
п.3. Решение неравенств с тангенсом
п.4. Решение неравенств с котангенсом
п.5. Примеры
Тригонометрические неравенства и методы их решения
💡 Видео

Видео:Решение тригонометрических неравенств. 10 класс.Скачать

Простейшие тригонометрические неравенства

п.1. Решение неравенств с синусом

Алгоритм решения неравенства (sinxgt a)

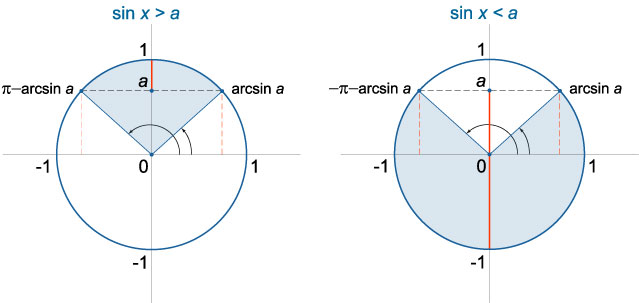
Шаг 1. В числовой окружности на оси синусов отметить точку с ординатой (a). Провести горизонталь (y=a), отметить точки её пересечения с окружностью.

Шаг 2. Решить уравнение (sin⁡x=a). Про решение простейших тригонометрических уравнений – см. §19 данного справочника. Полученные базовые решения являются значениями точек пересечения, подписать их.

Шаг 3. Дуга числовой окружности над проведенной горизонталью – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((arcsina+2pi k; pi-arcsin a+2pi k))

Решение тригонометрических неравенств при помощи окружности

$$ sin xgt frac12 $$ 1. Проводим горизонталь (y=frac12), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое).
2. Решаем уравнение (sinx=frac12) begin x=(-1)^kfracpi6+pi k= left[ begin fracpi6+2pi k\ frac+2pi k end right. end Подписываем точку справа (fracpi6) и точку слева (frac).
3. При обходе полученной дуги против часовой стрелки получаем интервал: ((fracpi6; frac)). Добавляем к концам интервала полный период.
Ответ: (left(fracpi6;+2pi k; frac+2pi kright))

Алгоритм решения неравенства (sinxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).

Алгоритм решения неравенства (sin⁡xlt a) будет отличаться тем, что в ответе нужно записывать дугу под горизонталью (y=a). При этом не забываем, что дугу нужно обходить в сторону возрастания. Поэтому угол слева пишут отрицательным (отсчитывая период назад).

Наконец, в неравенстве (sin⁡xleq a) всё будет то же, что и в (sin⁡xlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).

$$ sin xleq -frac<sqrt> $$ 1. Проводим горизонталь (y=-frac<sqrt>), отмечаем точки пересечения (закрашенные, т.к. неравенство нестрогое).
2. Решаем уравнение (sinx=-frac<sqrt>) begin x=(-1)^kleft(-fracpi4right)+pi k= left[ begin -frac+2pi k\ -frac+2pi k end right. end Подписываем точку справа (-frac) и точку слева (-frac).
3. При обходе полученной дуги против часовой стрелки получаем отрезок: (left[-frac;-fracright]). Добавляем к концам отрезка полный период.
Ответ: (left[-frac+2pi k;-frac+2pi kright])

п.2. Решение неравенств с косинусом

Алгоритм решения неравенства (cosxgt a)

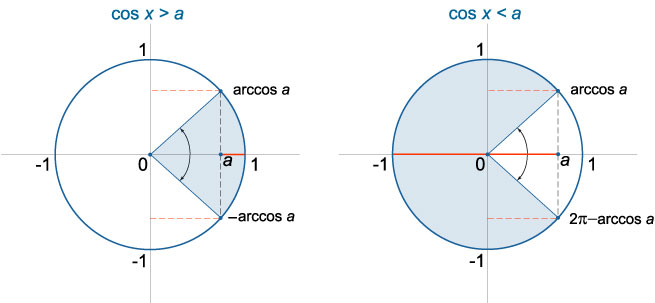
Шаг 1. В числовой окружности на оси косинусов отметить точку с абсциссой (a). Провести вертикаль (x=a), отметить точки её пересечения с окружностью.

Шаг 2. Решить уравнение (cos⁡x=a). Полученные базовые решения являются значениями точек пересечения, подписать их.

Шаг 3. Дуга числовой окружности справа от проведенной вертикали – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: ((-arccos⁡a+2pi k; arccos⁡a+2pi k))

$$ cosxgt frac<sqrt> $$ 1. Проводим вертикаль (x=frac<sqrt>), отмечаем точки пересечения (незакрашенные, т.к. неравенство строгое).
2. Решаем уравнение (cosx=frac<sqrt>) begin x=pmfracpi6+2pi k end Подписываем точку снизу (-fracpi6) и точку сверху (frac).
3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi6right)). Добавляем к концам интервала полный период.
Ответ: (left(-fracpi6;+2pi k; frac+2pi kright))

Алгоритм решения неравенства (cosxgeq a) будет таким же, только точки на числовой окружности будут закрашенными, и в ответе будет отрезок (с квадратными скобками).

Алгоритм решения неравенства (cosxlt a) будет отличаться тем, что в ответе нужно записывать дугу слева от вертикали (x=a). При этом не забываем, что дугу нужно обходить в сторону возрастания, сверху вниз. Значение угла снизу должно быть больше, чем угла сверху.

Наконец, в неравенстве (cos⁡xleq a) всё будет то же, что и в (cosxlt a). Только точки на концах будут закрашенными и войдут в ответ (с квадратными скобками).

п.3. Решение неравенств с тангенсом

Алгоритм решения неравенства (tgxgt a)

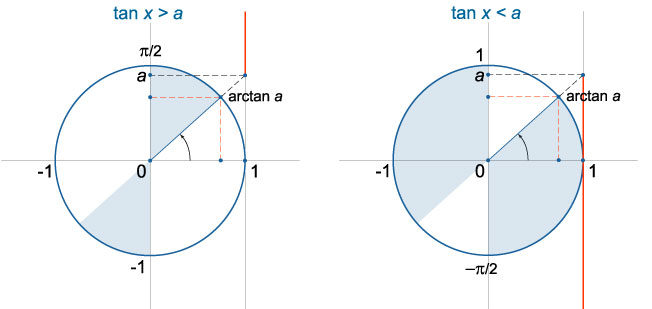
Шаг 1. На оси тангенсов (касательной к числовой окружности в точке (1,0)) отметить точку с ординатой (a). Провести луч из начала координат через отмеченную точку, отметить точку её пересечения с окружностью.

Шаг 2. Решить уравнение (tg⁡x=a). Полученное базовое решение является значением точки пересечения.

Шаг 3. Дуга числовой окружности от отмеченной точки до (fracpi2) (в которой (tgxrightarrow +infty)) – искомое решение. Записать ответ, обходя дугу против часовой стрелки. Добавить к концам полученного интервала полный период.
Решение имеет вид: (left(arctga+pi k; fracpi2+pi kright))

$$ tg xgt -frac<sqrt> $$ 1. На оси тангенсов отмечаем точку (-frac<sqrt>). Проводим луч из начала координат через эту точку.
2. Решаем уравнение (tgx=-frac<sqrt>) begin x=-fracpi6+pi k end Подписываем точку снизу (-fracpi6.) Верхней границей интервала будет (fracpi2), угол, в котором (tgxrightarrow +infty .)
3. При обходе полученной дуги против часовой стрелки получаем интервал: (left(-fracpi6;fracpi2right)). Добавляем к концам интервала период для тангенса.
Строго говоря, на числовой окружности длиной (2pi) получим две дуги для тангенса с периодом (pi). Ответ: (left(-fracpi6;+pi k; frac+pi kright))

Алгоритм решения неравенства (tg⁡xlt a) будет отличаться тем, что в ответе нужно записывать дугу от точки (-fracpi2) (в которой (tgxrightarrow -infty)) до найденного арктангенса.

Для нестрогих неравенств будут получаться полуинтервалы, в которых точки (pmfracpi2) ((tgxrightarrow pminfty)) будут ограничены круглой скобкой, а найденные арктангенсы – квадратной.

п.4. Решение неравенств с котангенсом

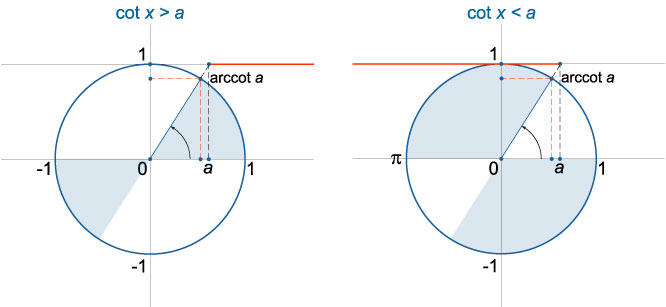
Решение неравенств с котангенсом аналогично решению с тангенсом. Для решения используется ось котангенсов (касательная к числовой окружности в точке (0;1)).

В неравенствах вида (ctgxgt a) пределу (ctgxrightarrow +infty) соответствует угол 0.

В неравенствах вида (ctgxlt a) пределу (ctgxrightarrow -infty) соответствует угол (pi).

п.5. Примеры

Пример 1. Решите неравенства:

a) (sinxleq frac<sqrt>) $$ xinleft[-frac+2pi k; frac+2pi kright] $$	б) (cosxlt -frac) $$ xinleft(frac+2pi k; frac+2pi kright) $$
в) (sinxgt -frac<sqrt>) $$ xinleft(-frac+2pi k; frac+2pi kright] $$	г) (tgxgeq 1) $$ xinleft.left(-frac+pi k; frac+pi kright.right] $$

Пример 2*. Решите неравенства:

a) (cosxgt -1)
Справа от вертикали (x=-1) расположена вся числовая окружность, кроме точки (pi).

Ответ: (xne pi+2pi k)б) (4cos^2frac x2-3leq 0)
(4cdot fracleq 3)
(2+2cosxleq 3)
(cosxleqfrac12)

Ответ: (left[fracpi3+2pi k; frac+2pi kright])

в) (-sqrtlt tgxleq 5)
(-arctgsqrt+pi klt xleq arctg5+pi k)
(-fracpi3+pi klt xleq arctg5+pi k)
Ответ: (left.left(-frac+pi k; arctg5+pi kright.right])

г) (tgleft(x-fracpi4right)gtsqrt)
(arctgsqrt+pi klt x-fracpi4ltfracpi2+pi k)
(fracpi4+fracpi3+pi klt xltfracpi4+fracpi2+pi k)
(frac+pi klt xltfrac+pi k)
Ответ: (left(frac+pi k; frac+pi kright))

Видео:РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ😉 #shorts #егэ #огэ #математика #профильныйегэСкачать

Тригонометрические неравенства и методы их решения

Тригонометрическими неравенствами называются неравенства, которые содержат переменную под знаком тригонометрической функции.

Методы решений неравенств:

Решение тригонометрических неравенств с помощью единичной окружности.
Графическое решение тригонометрических неравенств.
Решение неравенств методом интервалов.

При решении более сложных тригонометрических неравенств пользуются двумя основными приемами:

I. Данное неравенство с помощью равносильных преобразований сводится к простейшим тригонометрическим неравенствам. При выполнении преобразований пользуются теми же приемами, что и при решении тригонометрических уравнений.

II. Применяется метод интервалов для определения числовых промежутков, в которых содержатся решения неравенства. Предварительно решается соответствующее тригонометрическое уравнение и устанавливаются интервалы знакопостоянства с учетом области определения неравенства.

Неравенство (sinx>a)

При (|a|≥1) неравенство (sinx>a) не имеет решений: (xin varnothing) .
При (a решением неравенства (sinx>a) является любое действительное число: (xin mathbb R) .
При (−1≤a решение неравенства (sinx>a) выражается в виде (arcsin a + 2pi n .

Неравенство (sinx≥a)

Неравенство (sinx

Неравенство (sinx≤a)

Неравенство (cosx>a)

При (a≥1) неравенство (cosx>a) не имеет решений: (xin varnothing) .
При (a решением неравенства (cosx>a) является любое действительное число: (xin mathbb R) .
При (−1≤a решение неравенства (cosx>a) имеет вид (-arccos a + 2pi n .

Неравенство (cosx≥a)

Неравенство (cosx

Неравенство (cosx≤a)

Неравенство (tgx>a)

При любом действительном значении (a) решение строгого неравенства (tgx>a) имеет вид (arctg a + pi n .

Неравенство (tgx≥a)

Для любого значения (a) решение неравенства (tgx≥a) выражается в виде (arctg a + pi n le x .

Неравенство (tgx

Для любого значения (a) решение неравенства (tgx записывается в виде (-frac2 + pi n .

Неравенство (tgx≤a)

При любом (a) неравенство (tgx≤a) имеет следующее решение: (-frac2 + pi n .

Неравенство (ctgx>a)

При любом (a) решение неравенства (ctgx>a) имеет вид (pi n .

Неравенство (ctgx≥a )

Нестрогое неравенство (ctgx≥a) имеет аналогичное решение (pi n .

Неравенство (ctgx

Для любого значения (a) решение неравенства (ctgx лежит в открытом интервале (arcctg a + pi n .

Неравенство (ctgx≤a)

При любом (a) решение нестрогого неравенства (ctgx≤a) находится в полуоткрытом интервале (arcctg a + pi n le x .

Пример. Решите неравенство: (cosx>frac12) .

Решение: Данное неравенство можно решить двумя способами: графически и с помощью единичного круга. Рассмотрим каждый из способов.

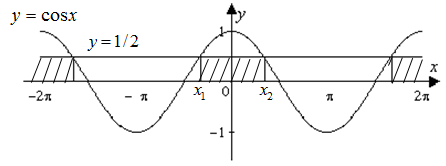
Первый способ. Изобразим в одной системе координат функции, описывающие левую и правую части неравенства, то есть (y=cosx и y=frac12) . Выделим промежутки, на которых график функции косинус (y=cosx) расположен выше графика прямой (y=frac12) .

Найдем абсциссы точек (x_1 и x_2) – точек пересечения графиков функций (y=cosx и y=frac12) , которые являются концами одного из промежутков, на котором выполняется указанное неравенство: (x_1=-arccosfrac12=-frac3; x_2=arccosfrac12=frac3) .

Учитывая, что косинус – функция периодическая, с периодом (2pi) , ответом будут значения x из промежутков ((-frac3+2pi k;frac3+2pi k), kin Z) .

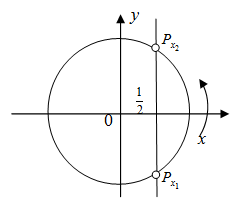
Второй способ. Построим единичную окружность и прямую (x=frac12) (так как на единичной окружности косинусам отвечает ось абсцисс). Обозначим (P_ и P_) – точки пересечения прямой и единичной окружности. Решением исходного уравнения будет множество точек абсциссы, которых меньше (frac12) . Найдем значение (x_1 и x_2) , совершая обход против часовой стрелки так, чтобы (x_1 :

Учитывая периодичность косинуса, окончательно получим интервалы ((-frac3+2pi k;frac3+2pi k), kin Z) .