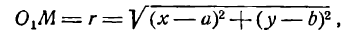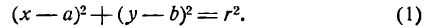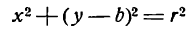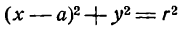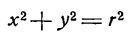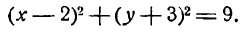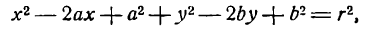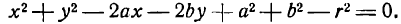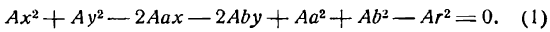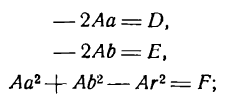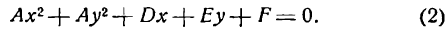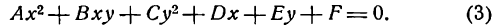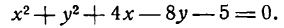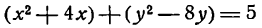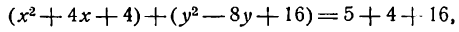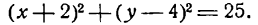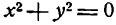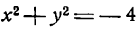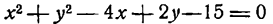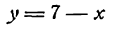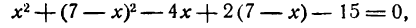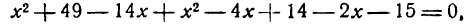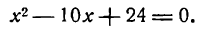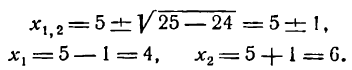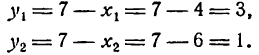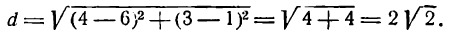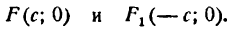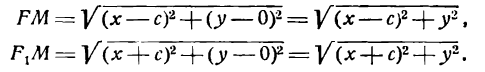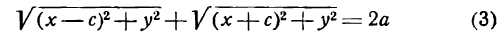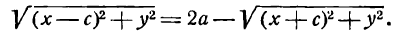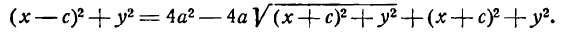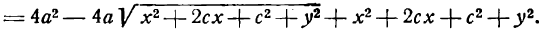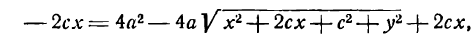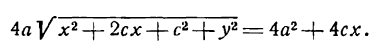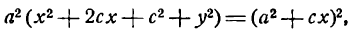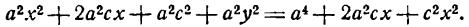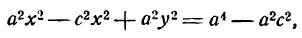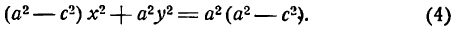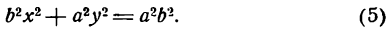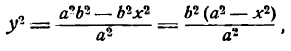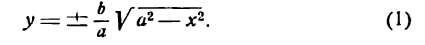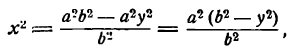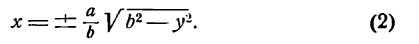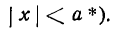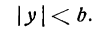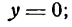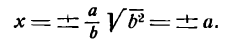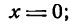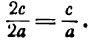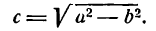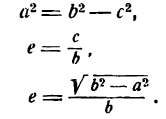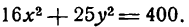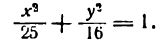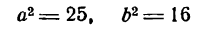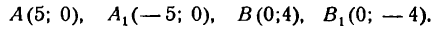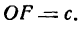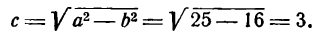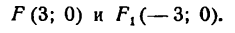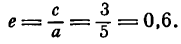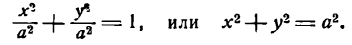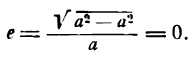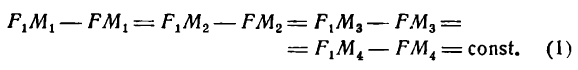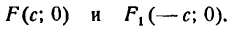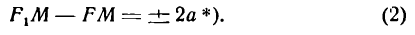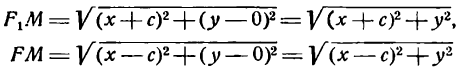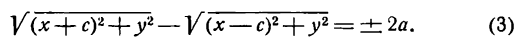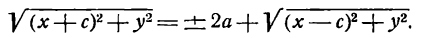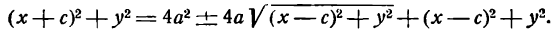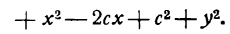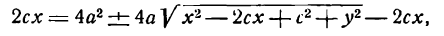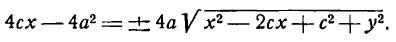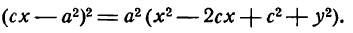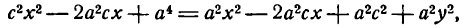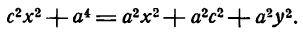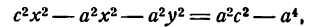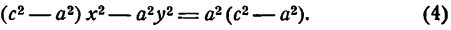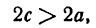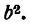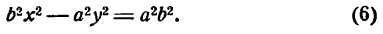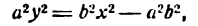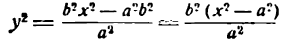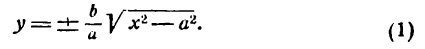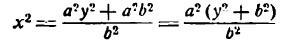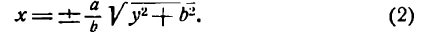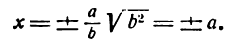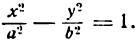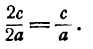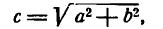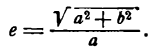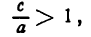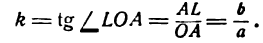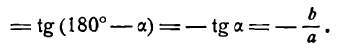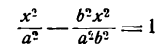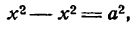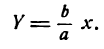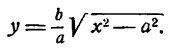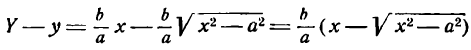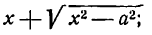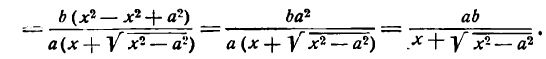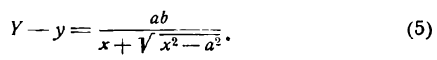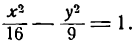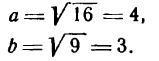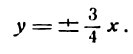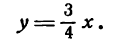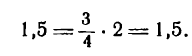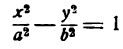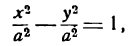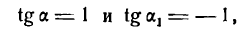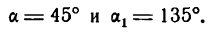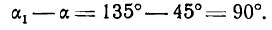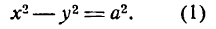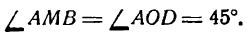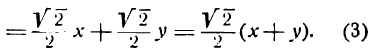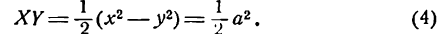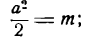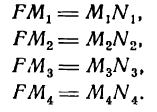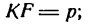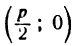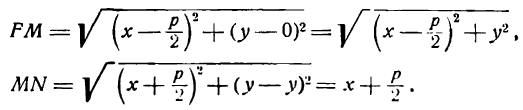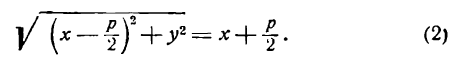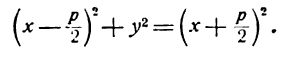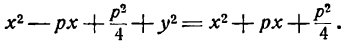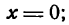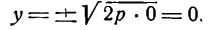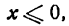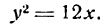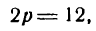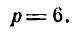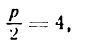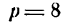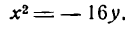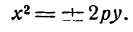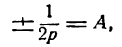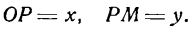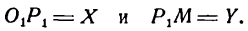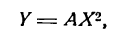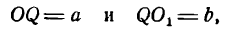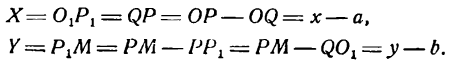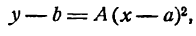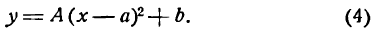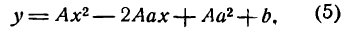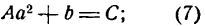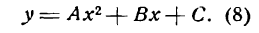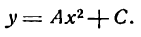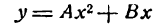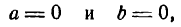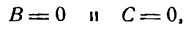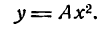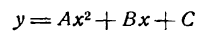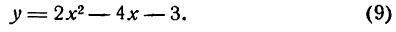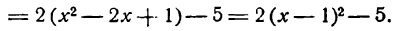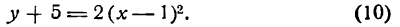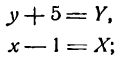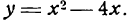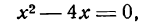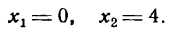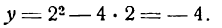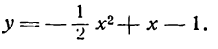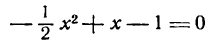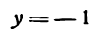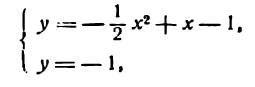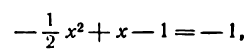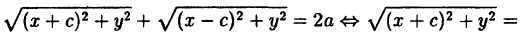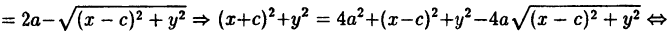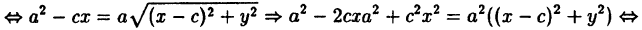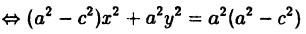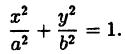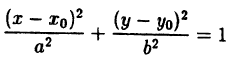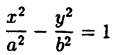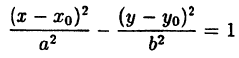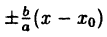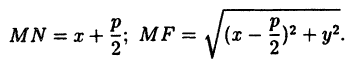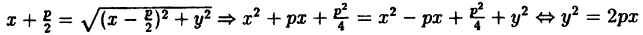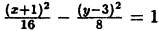МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО
Кафедра: Высшая математика
Тема: Кривые второго порядка
Выполнил: Студент группы 463-13
Принял: Старший препадаватель. Сайдалиев. З
Кривые второго порядка.
Понятие линии определилось в сознании человека в доисторические времена. Наблюдения за изгибами берега реки, траекторией брошенного камня, очертаниями листьев растений и цветов послужили основой для постепенного установления понятия кривой. Однако потребовалось очень много времени, прежде чем люди начали сравнивать между собой различные линии и отличать одну кривую от другой. Лишь в XVIIв. появилось абстрактное понятие линии, начались исследования свойств кривых.
Кривая (линия) — след, оставленный движущейся точкой или телом. Обычно кривую представляют лишь как плавно изгибающуюся линию, вроде параболы или окружности. Но математическое понятие кривой охватывает и прямую, и фигуры, составленные из отрезков прямых, например, треугольник или квадрат.
В школьном курсе математики в качестве кривых рассматриваются графики функций. В новых стандартах по математике профильного уровня обучения предусматривается изучение параболы, эллипса, гиперболы.
Некоторые понятия кривых встречаются нам в нашей повседневной жизни, хотя чаще всего мы этого не замечаем. Например, по круговой траектории движутся люди при катании на колесе обозрения, карусели, по гиперболе движутся альфа-частицы в опыте Резерфорда при рассеивании их ядром атома; по эллипсам движутся планеты вокруг Солнца, по параболе — тело в однородном поле силы тяжести, брошенное под углом к горизонту.
Знакомство с кривыми, изучение их свойств позволит расширить геометрические представления, углубить знания, повысить интерес к геометрии; создаст содержательную основу для дальнейшего изучения математики, физики и других наук.
Все вышесказанное подчеркивает актуальность выбранной темы дипломной работы.
Целью является изучение теории замечательных кривых.
Объектом исследования явились замечательные кривые, а также задачи, связанные с ними.
Предметом исследования является изучение теории замечательных кривых.
Цель исследования обусловила выбор следующих частных задач:
1. отобрать теоретический материал по теме дипломной работы;
2. обобщить и систематизировать материал;
. рассмотреть основные типы задач и их решение.
Структура дипломной работы следующая. Первая глава содержит теоретический материал по теории кривых. Здесь рассматриваются такие кривые, как окружность, эллипс, гипербола, парабола, а также кривые, наиболее часто встречающиеся в математическом анализе: Анъези локон, Декартов лист, Бернулли лемниската, кардиоида, цепная линия, астроида, циклоида.
Вторая часть дипломной работы представлена в виде рабочей тетради. Данная тетрадь разработана для студентов I и II-го курсов. В ней предлагаются задания по степени возрастания сложности по данной теме.
При работе над дипломной работой использовались в качестве основных источников учебники , , ,
- Замечательные кривые
- Кривые второго порядка. Общее уравнение кривой второго порядка.
- п.1. Окружность
- п.2. Эллипс
- Вывод канонического уравнения эллипса
- Эксцентриситет эллипса
- Эксцентриситет гиперболы
- Директрисы гиперболы
- п.4. Парабола
- Исследование формы параболы
- Реферат: Кривые второго порядка эллипс, окружность, парабола, гипербола
- Кривые второго порядка в математике с примерами решения и образцами выполнения
- Окружность и ее уравнения
- Эллипс и его каноническое уравнение
- Исследование формы эллипса по его уравнению
- Другие сведения об эллипсе
- Гипербола и ее каноническое уравнение
- Исследование формы гиперболы по ее уравнению
- Другие сведения о гиперболе
- Асимптоты гиперболы
- Эксцентриситет гиперболы
- Равносторонняя гипербола
- Парабола и ее каноническое уравнение
- Исследование формы параболы по ее уравнению
- Параллельный перенос параболы
- Уравнения кривых второго порядка как частные случаи общего уравнения второй степени с двумя переменными
- Дополнение к кривым второго порядка
- Эллипс
- Гипербола
- Парабола
- Пример задачи решаемой с применением кривых второго порядка
- Кривая второго порядка и её определение
- Окружность и ее уравнение
- Уравнение окружности как частный вид общего уравнения второй степени
- Эллипс и его уравнение
- Исследование уравнения эллипса
- Эксцентриситет эллипса
- Связь эллипса с окружностью
- Гипербола и ее уравнение
- Исследование уравнения гиперболы
- Эксцентриситет гиперболы
- Асимптоты гиперболы
- Равносторонняя гипербола
- Уравнение равносторонней гиперболы, отнесенной к асимптотам
- Парабола и ее простейшее уравнение
- Исследование уравнения параболы
- Уравнение параболы со смещенной вершиной и осью, параллельной оси Оу
- Конические сечения
- Кривая второго порядка и её вычисление
- Уравнение линии в декартовых и полярных координатах
- Окружность
- Эллипс
- Гипербола
- Парабола
- Понятие о приведении общего уравнения второго порядка к каноническому виду
- Решение заданий на тему: Кривые второго порядка
- 🌟 Видео
Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Замечательные кривые
Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Кривые второго порядка. Общее уравнение кривой второго порядка.
Важной задачей аналитической геометрии является исследование общего уравнения линии второго порядка и приведение его к простейшим (каноническим) формам.
Определение: Кривой второго порядка называется множество точек 


где коэффициенты А, 2В, С, 2D, 2E и F — любые числа и, кроме того, числа А, В и С не равны нулю одновременно, т. е. 
Уравнения окружности, эллипса, гиперболы и параболы являются частными случаями уравнения (1). ()
Теорема 1. Пусть в прямоугольной системе координат задано общее уравнение кривой второго порядка 
1) 
2) 
3) 
4) 
5) 
6) 
7) 
8) 
9) 
п.1. Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра). Окружность (рис.1) с центром в точке 


Раскрывая скобки, придадим уравнению (2) вид:

или 
где положено 
Уравнение (2») является уравнением второй степени. Итак, окружность имеет уравнение второй степени относительно текущих координат. Но, очевидно не всякое уравнение второй степени определяет окружность. Действительно, из уравнения (2» ) усматриваем, что в уравнении окружности коэффициенты при квадратах координат равны, а член с произведением координат 




Итак, по виду данного уравнения второй степени мы можем решить, является ли оно уравнением окружности или нет. Например, уравнение 


т. е. выделим из членов, содержащих 



После этого данное уравнение запишется так:
Перенося свободные члены вправо, будем иметь:
Сравнивая это уравнение с уравнением окружности (2), усматриваем, что 




Параметрические уравнения окружности:
Уравнение окружности в полярных координатах:
Отметим, что движение по окружности часто встречается в физике и технике, по круговой траектории движутся люди при катании на колесе обозрения, карусели, по круговым орбитам могут двигаться искусственные спутники Земли. Хорошо известна планетарная модель атома водорода по Резерфорду. В центре атома находится ядро, а электрон вращается вокруг него. (Энц. словарь юного математика)
п.2. Эллипс
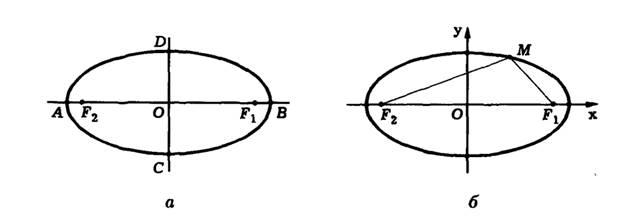
Название «Эллипс» ввёл Аполлоний Пергский, рассматривая эллипс как одно из конических сечений. Эллипс (греч. elleipsis — недостаток) — линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса.
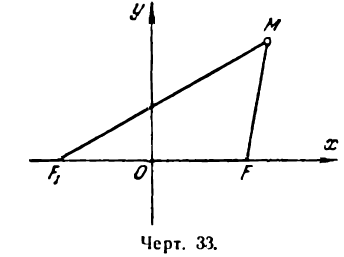
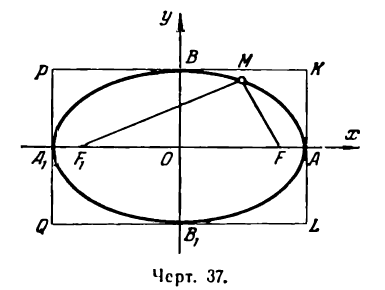
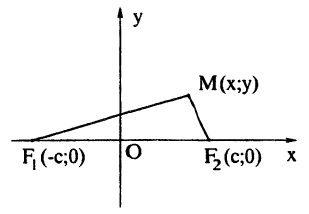
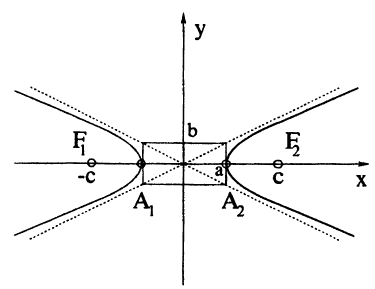
Определение: Эллипсом называется геометрическое место точек, для которых сумма расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина; требуется, чтобы эта постоянная была больше расстояния между фокусами. Фокусы эллипса принято обозначать через F1 и F2. ()
Пусть М — произвольная точка эллипса (рис 2.) с фокусами F1 и F2. Отрезки F1М и F2М (так же как и длины этих отрезков) называются фокальными радиусами точки М. Постоянную сумму фокальных радиусов точки эллипса принято обозначать через 2а. Таким образом, для любой точки М эллипса имеем:
М + F2М = const=2а> F1 F2 (3)
Данное неравенство необходимо: оно означает, что сумма двух сторон 
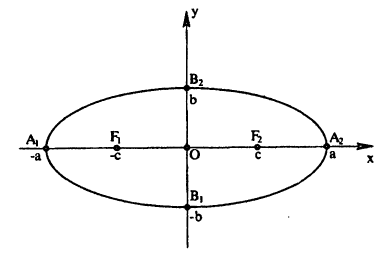
Середина 0 отрезка F1F2 (фокусного расстояния) называется центром эллипса. Расстояние F1 и F2 между фокусами обозначают через 2с.
Вывод канонического уравнения эллипса
Пусть дан какой-нибудь эллипс с фокусами F1, F2. (рис.3).
Возьмем на плоскости произвольную точку М и обозначим ее координаты через х и у. Обозначим, далее, через r1 и r2 расстояния от точки М до фокусов
(r1 = F1М, r2 = F2М).
Точка М будет находиться на данном эллипсе в том и только в том случае, когда
Чтобы получить искомое уравнение, нужно в равенстве заменить переменные r1 и r2 их выражениями через координаты х, у.
Заметим, что, так как F1 F2 = 2с и так как фокусы F1 и F2 расположены на оси Ох симметрично относительно начала координат, то они имеют соответственно координаты (-с; 0) и (+с; 0); учитывая это и применяя формулу расстояния между двумя точками, находим

Заменяя r1 и r2, получаем:

Это и есть уравнение рассматриваемого эллипса, так как ему удовлетворяют координаты точки М (х; у), когда точка М лежит на этом эллипсе. Возведём обе части равенства в квадрат, получим:

Возводя в квадрат обе части последнего равенства, найдем:

Здесь мы введем в рассмотрение новую величину

Так как по условию а>с, следовательно, 
тогда уравнение (8) можно переписать в виде
Разделив обе части этого равенства на a2b2, окончательно получим

Это уравнение называется каноническим уравнением эллипса, где а и b — длины большой и малой полуосей эллипса. При a = b фокусы F1 и F2 совпадают, и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса. Уравнение 
Эксцентриситет эллипса
Определение: Эксцентриситетом эллипса называется отношение расстояния между фокусами этого эллипса к длине его большой оси (Шипачев); обозначив эксцентриситет буквой е, получаем:

Заметим, что 


Следовательно, эксцентриситет определяется отношением осей эллипса, а отношение осей, в свою очередь, определяется эксцентриситетом. Таким образом, эксцентриситет характеризует форму эллипса. Чем ближе эксцентриситет к единице, тем меньше 1- е2, тем меньше, следовательно, отношение 


Это уравнение является уравнением окружности с центром в начале координат и с радиусом равным а. Значит, окружность можно рассматривать как частный случай эллипса, когда полуоси его равны между собой и эксцентриситет равен нулю:
Эксцентриситет эллипса характеризует меру вытянутости эллипса.
Как известно, планеты и некоторые кометы движутся по эллиптическим орбитам. Оказывается, что эксцентриситеты планетных орбит весьма малы, а кометных — велики, т. е. близки к единице. Таким образом, планеты движутся почти по окружности, а кометы то приближаются к Солнцу (Солнце находится в одном из фокусов), то удаляются от него.
Определение: Две прямые, перпендикулярные к большой оси эллипса и расположенные симметрично относительно центра на расстоянии 
Уравнения директрис в выбранной системе координат имеют вид:


Первую из них мы условимся называть левой, вторую — правой. Так как для эллипса 
Поэтому уравнение (15) принимает вид:


Уравнение 
Эксцентриситет гиперболы
Гипербола состоит из двух ветвей (правой и левой) и имеет две асимптоты:

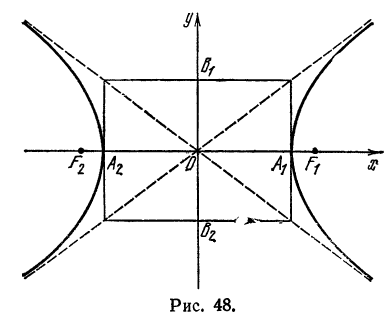
Оси симметрии называются осями гиперболы, а центр симметрии (точка пересечения осей) — центром гиперболы. Одна из осей пересекается с гиперболой в двух точках, которые называются ее вершинами (на рис.7 они обозначены буквами А и А′ ). Эта ось называется действительной осью гиперболы. Другая ось не имеет общих точек с гиперболой и называется мнимой осью гиперболы. Прямоугольник со сторонами 2а и 2b (см. рис.7) называется основным прямоугольником гиперболы. Величины а и b называются соответственно действительной и мнимой полуосями гиперболы.

переставляя буквы х и у, а и b, можно привести к виду (17). Отсюда ясно, что уравнение (18) определяет гиперболу, расположенную так, как показано на рис.7 справа; вершины ее лежат на оси Оу. Эта гипербола называется сопряженной по отношению к гиперболе (17) (). Обе гиперболы имеют одни и те же асимптоты.
Гипербола с равными полуосями (а = b) называется равносторонней, и ее каноническое уравнение имеет вид

Так как основной прямоугольник равносторонней гиперболы является квадратом, то асимптоты равносторонней гиперболы перпендикулярны друг другу.
Определение: Эксцентриситетом гиперболы называется отношение расстояния между фокусами этой гиперболы к расстоянию между ее вершинами (); обозначив эксцентриситет буквой е, получим:

Так как с > a, то е > 1, т. е. эксцентриситет гиперболы больше единицы.
Заметим, что 



Из последнего равенства легко получить геометрическое истолкование эксцентриситета гиперболы. Эксцентриситет определяется отношением 

Чем меньше эксцентриситет, т. е. чем ближе он к единице, тем меньше 

В случае равносторонней гиперболы a = b и е = √2.
Директрисы гиперболы
Определение: Две прямые, перпендикулярные к той оси гиперболы, которая ее пересекает, и расположенные симметрично относительно центра на расстоянии 
Уравнения директрис в выбранной системе координат имеют вид


Первую из них мы условимся называть левой, вторую — правой.
Так как для гиперболы е >1, то 
Установленное свойство эллипса и гиперболы можно положить в основу общего определения этих линий:
Множество точек, для которых отношение расстояний до фокуса и до соответствующей директрисы величина постоянная, равная е, это эллипс, если е 1. ()
Возникает вопрос, что представляет собой множество точек, определенное аналогичным образом при условии 
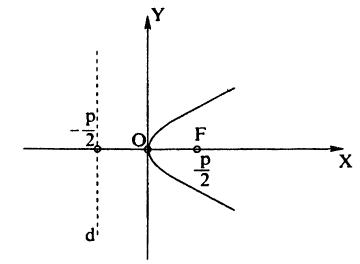
п.4. Парабола
Парабола (греч. parabole) — кривая второго порядка.
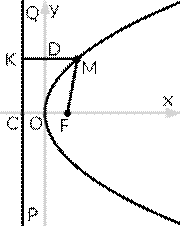
Определение: Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой (предполагается, что эта прямая не проходит через фокус). ()
Фокус параболы принято обозначать буквой F, расстояние от фокуса до директрисы — буквой p. Величину р называют параметром параболы.
Пусть дана какая-нибудь парабола (рис.11). Возьмем на плоскости произвольную точку М и обозначим ее координаты через х и у. Обозначим далее через r расстояние от точки М до фокуса F(r=
Вывод канонического уравнения параболы
Чтобы получить искомое уравнение, нужно заменить переменные r и d их выражениями через текущие координаты х, у.
Заметим, что фокус F имеет координаты 

Обозначим через N основание перпендикуляра, опущенного из точки М на директрису. Очевидно, точка N имеет координаты 




Заменяя в равенстве (20) r и d выражениями (21) и (22), найдем

Это и есть уравнение рассматриваемой параболы, так как ему удовлетворяют координаты точки М (х; у), когда точка М лежит на данной параболе. Приведем его к более удобному виду, для чего возведем обе части равенства (23) в квадрат. Получаем:
Проверим, что уравнение (24), полученное возведением в квадрат обеих частей равенства (23), не приобрело «лишних» корней. Для этого достаточно показать, что для любой точки, координаты х и у которой удовлетворяют уравнению (22), выполнено соотношение (20). Действительно, из уравнения (24) вытекает, что х ≥ 0, поэтому для точек с неотрицательными абсциссами имеем d = 

Уравнение (24) называется каноническим уравнением параболы. Уравнение у2=2рх, определяющее параболу в некоторой системе декартовых прямоугольных координат, есть уравнение второй степени; таким образом, парабола есть линия второго порядка. ()
Исследование формы параболы
Исследуем теперь форму параболы по ее каноническому уравнению. Так как уравнение (24) содержит у только в четвертой степени, то парабола симметрична относительно оси Ох. Следовательно, достаточно рассмотреть только ее часть, лежащую в верхней полуплоскости. Для этой части у ≥ 0, поэтому, разрешая уравнение (24) относительно у, получаем:
у = 
Из равенства (25) вытекают следующие утверждения:
1. если х 0, расположена слева от оси ординат (Рис.10, б). Вершина этой параболы совпадает с началом координат, осью симметрии является ось Ох.
Видео:#198. ЭЛЛИПС, ГИПЕРБОЛА, ПАРАБОЛАСкачать

Реферат: Кривые второго порядка эллипс, окружность, парабола, гипербола
| Название: Кривые второго порядка эллипс, окружность, парабола, гипербола Раздел: Рефераты по математике Тип: реферат Добавлен 18:40:40 24 сентября 2011 Похожие работы Просмотров: 3021 Комментариев: 11 Оценило: 12 человек Средний балл: 4.3 Оценка: 4 Скачать | ||||||||||||||||||
| Кривая второго порядка — это некоторая линия на плоскости, которая в декартовой системе координат задается общим уравнением |
Окружность и ее уравнение
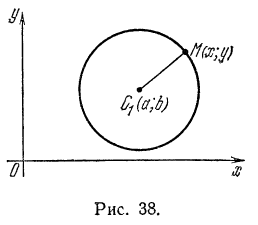
Окружностью называется геометрическое место точек, одинаково удаленных от одной точки, называемой центром.
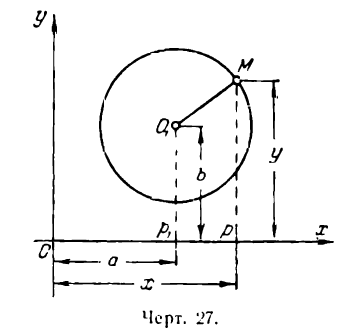
Пользуясь этим определением, выведем уравнение окружности. Пусть радиус ее равен r, а центр находится в точке
О1(а; b). Возьмем на окружности произвольную точку М(х; у) (рис. 27).
По формуле расстояния между двумя точками можем написать:
или, после возведения обеих частей равенства в квадрат,
Так как точка М нами взята произвольно, а радиус r — величина постоянная, то равенство (1) справедливо для всех точек окружности, т. е. координаты любой ее точки удовлетворяют этому равенству. А если так, то равенство (1) нужно рассматривать как уравнение окружности.
В уравнении (1) а и b — координаты центра окружности, а х и у — текущие координаты.
Если положить а = 0, то уравнение (1) обратится в следующее:
и будет определять окружность с центром на оси Оу (рис. 28).
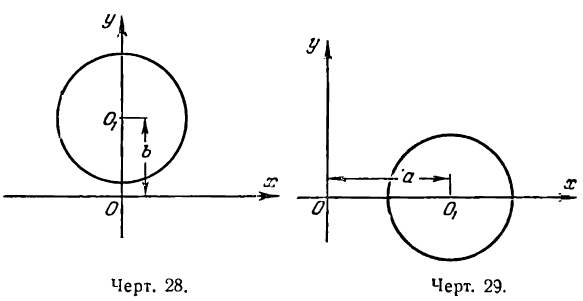
При b = 0 уравнение (1) примет вид
и будет определять окружность с центром на оси Ох (рис. 29).
Наконец, при а = 0 и b = 0 уравнение (1) преобразуется в следующее:
и будет определять окружность с центром в начале координат (рис. 30).
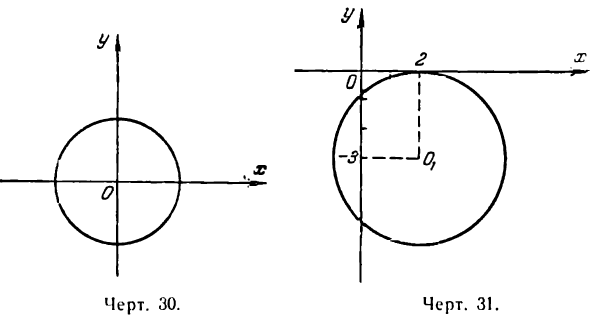
Можно построить окружность, имея ее уравнение. Пусть, например, требуется построить окружность
Перепишем это уравнение в следующем виде:
сравнивая это уравнение с(1), видим, что координаты центра окружности суть (2; — 3) и радиус ее r = 3. Построив
точку О1(2;—3), опишем из нее радиусом, равным 3 единицам масштаба, искомую окружность (рис. 31).
Уравнение окружности как частный вид общего уравнения второй степени
Раскрыв скобки в уравнении (1) , можем написать:
Умножив все члены последнего равенства на А, получим:
тогда уравнение (1) окружности примет вид
Уравнение (2) является частным случаем общего уравнения второй степени с двумя переменными. В самом деле, сравним уравнение (2) с общим уравнением второй степени с двумя переменными, имеющим, как известно, следующий вид:
Мы видим, что уравнение (2) отличается от уравнения (3) только тем, что у первого коэффициенты при х2 и у2 одинаковы и отсутствует член, содержащий произведение ху.
Таким образом, окружность определяется общим уравнением второй степени с двумя переменными, если в нем коэффициенты при х2 и у2 равны между собой и отсутствует член с произведением ху.
Обратно, уравнение вида (2), вообще говоря, определяет окружность. Убедимся в этом на примере. Пусть дано уравнение
Перепишем его в следующем виде:
и преобразуем двучлены, стоящие в скобках, в полные квадраты суммы и разности, прибавив к первому 4, ко второму 16. Чтобы равенство при этом не нарушилось, увеличим и правую часть его на сумму 4+16. Получим:
Последнее равенство является уравнением окружности, имеющей радиус, равный 5, и центр в точке О1(-2; 4).
Бывают однако случаи, когда уравнение (2) при некоторых значениях коэффициентов не определяет окружности; например, уравнению
удовлетворяют координаты единственной точки (0; 0), а уравнению
не удовлетворяют координаты ни одной точки, так как сумма квадратов действительных чисел не может иметь отрицательного значения.
Пример:
и хорда 
Решение:
Так как концы хорды являются общими точками окружности и хорды, то их координаты удовлетворяют как уравнению первой, так и уравнению второй линии. Поэтому, чтобы найти эти координаты, нужно решить совместно уравнения окружности и хорды. Подставив значение
в уравнение окружности, получим:
Находим значение у:
Итак, концами хорды служат точки с координатами (4; 3) и (6; 1).
По формуле расстояния между двумя точками можем определить искомую длину хорды
Эллипс и его уравнение
Эллипсом называется геометрическое место точек, сумма расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная (и болыиая, чем расстояние между фокусами).
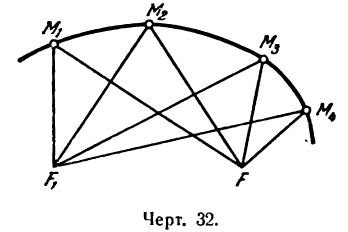
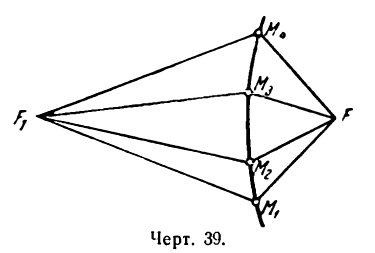
Пусть, например, на эллипсе взяты точки М1, M2, M3, М4 и т. д. (рис. 32). Если фокусы обозначить через F и F1, то согласно данному определению можно написать:
Геометрическое место точек, обладающих вышеуказанным свойствам (1), и есть эллипс.
На основании определения эллипса составим его уравнение. Для этого выберем систему координат следующим образом. За ось Ох примем прямую, проходящую через фокусы F и F1, а за ось Оу — прямую перпендикулярную
к FF1 и проведенную через середину отрезка FF1 (рис. 33). Обозначим расстояние F1F между фокусами через 2с, тогда координаты фокусов будут:
Возьмем на эллипсе произвольную точку М(х;у). Обозначим постоянную величину суммы расстояний каждой точки от фокусов через 2а, тогда
По формуле расстояния между двумя точками найдем:
Теперь равенство (2) перепишется следующим образом:
и будет представлять уравнение эллипса в принятой системе координат.
Упростим уравнение (3). Для этого перенесем один из радикалов в правую часть уравнения:
Возведем обе части этого равенства в квадрат:
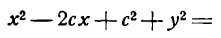
Приведем подобные члены:
Сократив на 4 и снова возведя в квадрат обе части равенства, получим:
Перенесем все члены, содержащие х и у, в левую часть равенства, остальные члены — в правую:
Но согласно определению эллипса
Из последнего неравенства следует, что 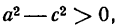
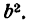
Наконец, разделим все члены последнего равенства на 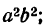
где х и у — текущие координаты точек эллипса, а
Уравнение (6) и есть простейший вид уравнения эллипса *).
*) Уравнение (6) получилось в результате двукратного возведения в квадрат уравнения (3), благодаря чему, вообще говоря, возможно появление посторонних корней. Можно показать, что уравнение (6) не имеет посторонних корней, т. е. любая точка, координаты которой удовлетворяют уравнению (6), лежит на эллипсе.
Исследование уравнения эллипса
Определим сначала у из уравнения (5) :
Из того же уравнения (5) найдем:
Рассмотрим теперь равенства (1) и (2).
I. Пусть
*) | х | означает, что х берется по абсолютной величине; таким образом, запись | х |
Тогда каждому значению у, как мы видим из равенства (2), отвечают два значения х равные по абсолютной величине, но с разными знаками. Отсюда следует, что каждому значению у соответствуют на эллипсе две точки, симметричные относительно оси Оу.
Из сказанного заключаем: эллипс 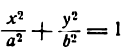
II. Найдем точки пересечения эллипса с осью Ох. Пусть
тогда из равенства (2) имеем:
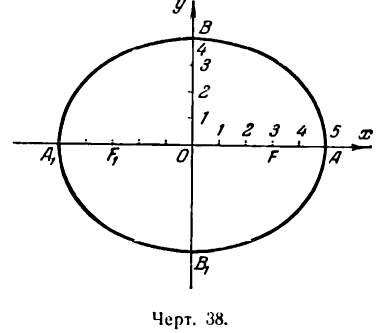
Отсюда следует: эллипс пересекает ось Ох в двух точках, координаты которых (а; 0) и (— а; 0) (точки А и А1 на рис. 34).
III. Найдем точки пересечения эллипса с осью Оу. Пусть
тогда из равенства (1) имеем:
Отсюда заключаем, что эллипс пересекает ось Оу в двух точках, координаты которых (0; b) и (0; —b) (точки В и В1 на рис. 35).
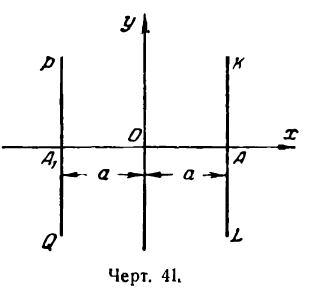
IV. Пусть х принимает такие значения, что
тогда выражение под корнем в равенстве (1) будет отрицательным, и, следовательно, у будет иметь мнимые значения. А это значит, что не существует точек эллипса, абсциссы которых удовлетворяют условию (3), т. е. эллипс расположен внутри полосы, заключенной между прямыми х = + а и х = — а (рис. 34, прямые КL и РQ).
Если же положить
то из равенства (2) получим для х мнимые значения. Это говорит о том, что точки, удовлетворяющие условию (4), на эллипсе не лежат, т. е. эллипс заключен между прямыми у = + b и у = — b (рис. 35, прямые РК и QL .
Из сказанного следует, что все точка эллипса лежат внутри прямоугольника, стороны которого параллельны координатным осям и имеют длины, равные 2а и 2b, а диагонали пересекаются в начале координат (рис. 36).
Эллипс имеет форму, показанную на рис. 37, Точки A,, A1, В и В1 называются вершинами эллипса, а точка О — его центром. Отрезок А1А = 2а называется его большой осью, а отрезок В1В = 2b — малой осью, Отрезки FМ и F1М носят название фокальных радиусов точки М.
Эксцентриситет эллипса
Эксцентриситетом эллипса называется отношение расстояния между его фокусами к длине большой оси, т. e.
Эксцентриситет обычно обозначают буквой е. Таким образом,
Но согласно формуле (7)
Поэтому для определения эксцентриситета может служить
Так как 0 а уравнение (6) представляет эллипс, фокусы которого лежат на оси Оу; в этом случае его большая ось равна 2 b , а малая 2 а . В соответствии с этим формула (7) и формулы (1) и (2) настоящей лекции примут такой вид:
Пример:
Определить длину его осей, координаты вершин и фокусов, а также величину эксцентриситета.
Решение:
Разделив обе части данного уравнения на 400, получим:
Итак, большая ось эллипса 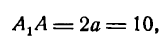
Координаты вершин его будут:
Чтобы найти координаты фокусов, нужно узнать величину
Из равенства (7) имеем:
Следовательно, координаты фокусов будут:
Наконец, по формуле (1) настоящей лекции находим:
Связь эллипса с окружностью
Положим, что полуоси эллипса равны между собой, т. е. а = b, тогда уравнение эллипса примет вид
Полученное уравнение, как известно, определяет окружность радиуса, равного а.
Посмотрим, чему будет равен эксцентриситет в этом случае; полагая в формуле (2)
Отсюда заключаем, что окружность есть частный случай эллипса, у которого полуоси равны между собой, а следовательно, эксцентриситет равен нулю.
Гипербола и ее уравнение
Гиперболой называется геометрическое место точек, разность расстояний каждой из которых от двух данных точек, называемых фокусами, есть величина постоянная (эта постоянная берется по абсолютному значению, причем она меньше расстояния между фокусами и не равна нулю).
Пусть, например, точки М1, М2, M3, М4 лежат на гиперболе, фокусы которой находятся в точках F и F1 (рис. 39). Тогда, согласно данному выше определению, можно написать:
Пользуясь определением гиперболы, выведем ее уравнение.
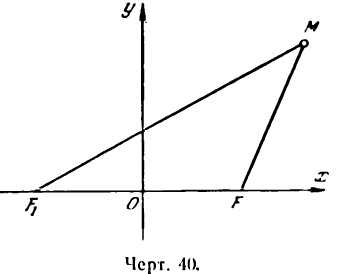
Примем за ось Ох прямую, проходящую через фокусы F и F1 (рис. 40), а за ось Оу — прямую, перпендикулярную к отрезку F1F и делящую его пополам.
Положим F1F = 2c тогда координаты фокусов будут
Возьмем на гиперболе произвольную точку М(х; у) и обозначим величину разности расстояний каждой точки от фокусов через 2а; тогда
По формуле расстояния между двумя точками найдем:
и, заменив в равенстве (2) F1М и FМ их выражениями, напишем:
Это и есть уравнение гиперболы относительно выбранной системы координат, так как оно согласно равенствам (1) справедливо для любой ее точки.
*) Знак + берется в случае, если F1М > FМ , и знак —, если F1М
Возведем обе части уравнения в квадрат:
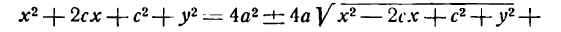
Приведем подобные члены:
Сократив на 4, снова возведем в квадрат обе части уравнения; получим:
Перенесем в левую часть члены, содержащие х и у, а остальные члены в правую:
Согласно определению гиперболы
При условии (5) разность 
Сделав это в равенстве (4), получим:
Разделив последнее равенство на 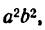
где х и у— текущие координаты точек гиперболы, а
Равенство (7) представляет собой простейший вид уравнения гиперболы *).
*) Как и в случае эллипса, можно показать, что уравнение (7) равносильно уравнению (3), т. е. не имеет посторонних корней.
Исследование уравнения гиперболы
Из уравнения (6) имеем:
Из этого же уравнения (6) находим:
Исследуем уравнения (1) и (2) для выяснения геометрической формы гиперболы.
I. Найдем точки пересечения гиперболы с осью Ох. Для этого полагаем, у = 0 и из уравнения (2) получаем:
Отсюда следует: гипербола пересекает ось Ох в двух точках, координаты которых (а; 0) и (— а; 0) (рис. 41, точки А и А1).
II. Положим в уравнении (1)
тогда у получит мнимое значение, а это значит, что на гиперболе нет точек, удовлетворяющих условию (3). Следовательно, в полосе между прямыми х = + а и х = — а (прямые KL и РQ на рис. 41) нет точек гиперболы
III. Пусть
тогда из равенства (1) найдем для каждого х два действительных значения у, равных по абсолютной величине, но с противоположными знаками. А это значит, что каждому значению х, удовлетворяющему неравенству (4), соответствуют на нашей кривой две точки, симметричные относительно оси Ох.
Следовательно, гипербола 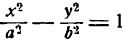
С другой стороны, для каждого значения у из равенства (2) найдем два действительных значения х, равных по абсолютной величине, но противоположных по знаку, т. е. каждому значению у на гиперболе соответствуют две точки, симметричные относительно оси Оу.
Следовательно, гипербола 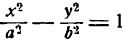
IV. Если в уравнении (1) давать х значения, заключенные между +a и 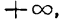
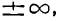
Если же давать х значения, заключенные между — а и 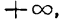
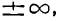
Из всего изложенного следует, что гипербола
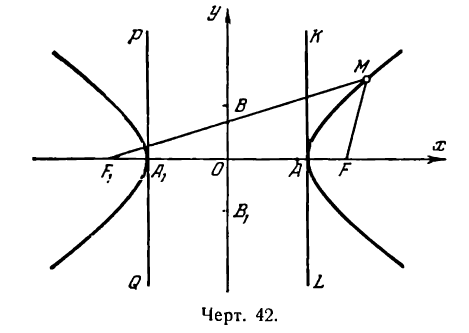
состоит из двух симметричных относительно оси Оу бесконечных ветвей, одна из которых расположена справа от
прямой х = + а, а другая слева от прямой х = — а. Каждая из этих ветвей симметрична относительно оси Ох (рис. 42).
Точки А(а; 0) и А1(- а; 0) называются вершинами гиперболы, а точка О (0; 0) — ее центром.
Отрезок АА1 = 2а носит название действительной или вещественной оси гиперболы в отличие от оси ВВ1 = 2b, называемой мнимой *).
*) Отрезок ВВ1 = 2b называется мнимой осью, так как на нем нет точек гиперболы.
Отрезки F1М и FМ — фокальные радиусы точки М.
Эксцентриситет гиперболы
Эксцентриситетом гиперболы называется отношение расстояния между фокусами к длине вещественной оси, т. е.
Эксцентриситет гиперболы, так же как и для эллипса, обозначается буквой е:
Но согласно равенству (8)
поэтому формулу (1) можно представить в следующем виде:
Так как для гиперболы с > а , то дробь
а потому эксцентриситет гиперболы больше единицы.
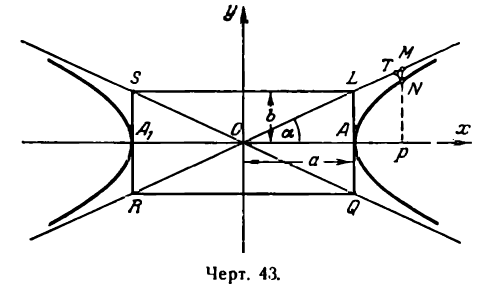
Асимптоты гиперболы
Построим на осях гиперболы
прямоугольник LQRS со сторонами, равными 2а и 2b и проведем его диагонали LR и QS продолжив их по обе стороны (рис. 43).
Прямая LR проходит через начало координат, поэтому ее уравнение будет:
Но угловой коэффициент
Заменив в уравнении (1) 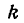
Прямая QS также определяется уравнением (1), но угловой коэффициент ее будет уже другой, а именно:
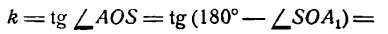
Таким образом, уравнение прямой QS будет:
Обычно уравнения (2) и (3) записывают следующим образом:
Между прямыми, представленными уравнениями (4), и гиперболой существует связь; выясним ее.
Решим совместно способом подстановки уравнения (4) и
уравнение гиперболы
что невозможно, так как
Таким образом, прямые (4) х2 уа
и гипербола 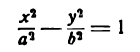
Возьмем на прямой LR и на гиперболе точки М и N, расположенные в первом координатном углу и имеющие одну и ту же абсциссу. Ординатой точки М служит РМ; обозначим ее через Y в отличие от ординаты точки N которую обозначим буквой у. Из уравнения (2) можно написать:
Из уравнения гиперболы имеем:
и посмотрим, как она будет изменяться при возрастании абсциссы. Для этого умножим и разделим правую часть последнего равенства на выражение
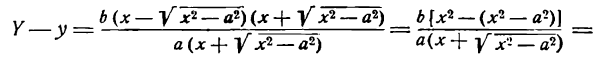
Пусть величина х в равенстве (5) бесконечно возрастает, тогда знаменатель дроби также бесконечно растет, а сама дробь уменьшается, приближаясь к нулю. Таким образом, гипотенуза NМ и, следовательно, катет NT в прямоугольном треугольнике МNТ стремится к нулю. Из сказанного делаем вывод: при неограниченном возрастании абсциссы х гипербола приближается к прямой LR как угодно близко, нигде ее не пересекая.
Так как прямые LR и QS, а также точки гиперболы симметричны относительно оси Ох, то можно сказать, что и часть гиперболы, расположенная в четвертом координатном углу, как угодно близко подходит к прямой QS , нигде ее не пересекая.
Вывод, сделанный для правой ветви гиперболы, справедлив и для ее левой ветви благодаря той же симметричности прямых (4) и гиперболы относительно координатных осей.
называются асимптотами гиперболы.
Из сказанного в настоящей лекции можно сделать заключение, что гипербола расположена всеми своими точками внутри вертикальных углов, образуемых асимптотами, и нигде не выходит за их границы. Этим обстоятельством можно воспользоваться для построения гиперболы в случае, если не требуется точного, а достаточно только приближенного ее изображения; для этого, нарисив асимптоты, нужно провести плавную кривую линию, постепенно приближая ее к асимптотам.
Пример:
Дана гипербола
Узнать, лежит ли точка A(2; 1,5) на какой-либо ее асимптоте.
Решение:
Из данного уравнения имеем:
Следовательно, уравнения асимптот будут:
Так как точка А лежит согласно условию в первом координатном углу, то она может принадлежать только асимптоте, определяемой уравнением
Подставив в него вместо х и у координаты точки А, получим тождество:
Значит, точка А лежит на указанной асимптоте гиперболы.
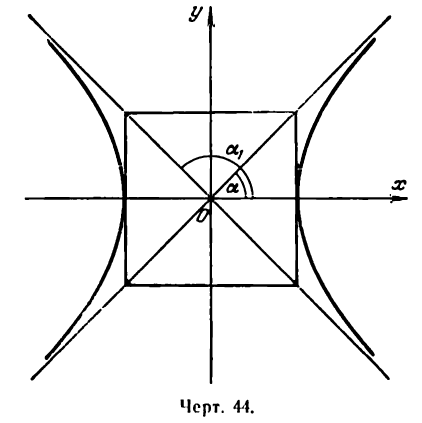
Равносторонняя гипербола
Если в уравнении гиперболы
положим а = b то это уравнение примет вид
Уравнение (1) определяет гиперболу, у которой полуоси равны между собой. Такая гипербола называется равносторонней. Уравнения асимптот в этом случае будут:
так как отношение
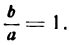
Как видно из уравнения (2), угловые коэффициенты асимптот равны + 1 и —1 . Если обозначить углы, образуемые асимптотами с положительным направлением оси Ох, соответственно через а и а1 (рис. 44), то
Следовательно, угол между асимптотами будет:
Отсюда заключаем: асимптоты равносторонней гиперболы взаимно перпендикулярны.
Уравнение равносторонней гиперболы, отнесенной к асимптотам
Так как асимптоты равносторонней гиперболы взаимно перпендикулярны, то их можно принять за оси прямоугольной системы координат и рассматривать гиперболу по отношению к этим новым осям. Выведем уравнение равносторонней гиперболы для этого случая.
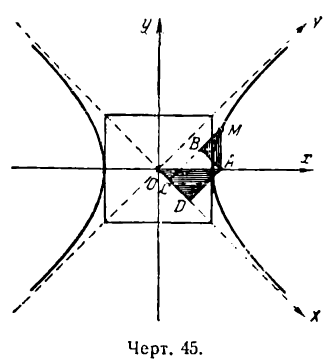
Пусть дана равносторонняя гипербола. Тогда ее уравнение по отношению к координатным осям Ох и Оу (рис. 45)
выразится, как было пока-* у зано в , в виде
Взяв на гиперболе произвольную точку М (х; у) и построив ее координаты, будем иметь:
Примем теперь за оси координат асимптоты гиперболы: ОХ— за ось абсцисс, ОY — за ось ординат. Опустив перпендикуляр МС на новую ось абсцисс, найдем:
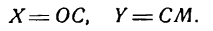
Выразим новые координаты X н Y точки М через старые х и у. Для этого из точки А проведем 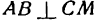
Обратим внимание на то, что в образовавшихся прямоугольных треугольниках АМВ и АОD
как углы, образованные взаимно перпендикулярными прямыми. Но
Из рисежа имеем:
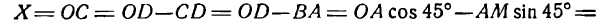
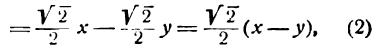
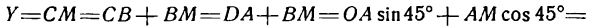
Перемножив равенства (2) и (3) и приняв во внимание равенство (1), получим:
Положим для краткости
тогда равенство (4) перепишется так:
где m— постоянная величина.
Таково уравнение равносторонней гиперболы, если за оси координат принять ее асимптоты.
Как видно из уравнения (5), переменные X и Y — величины обратно пропорциональные, а потому можно сказать, что равносторонняя гипербола ху = m представляет собой график обратно пропорциональной зависимости между переменными величинами.
Парабола и ее простейшее уравнение
Параболой называется геометрическое место точек, каждая из которых одинаково удалена от точки, называемой фокусом, и от прямой, называемой директрисой <при условии, что фокус не лежит на директрисе).
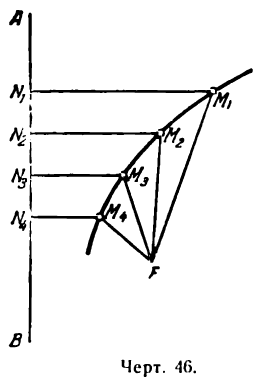
Пусть точки М1 М2, М3, М4 лежат на параболе (рис. 46).
Если точка F изображает фокус, а прямая АВ— директрису, то согласно данному выше определению можем написать:
Выведем уравнение параболы, пользуясь ее определением. Для этого выберем систему координат, приняв за ось Ох прямую, проведенную через точку F (фокус) перпендикулярно к директрисе АВ, а за
ось Оу — прямую, проходящую через середину отрезка КF перпендикулярно к последнему (рис. 47). Обозначим
тогда координаты фокуса F будут
Возьмем на параболе произвольную точку М(x; у) расстояния ее от фокуса F и от директрисы АВ будут выражаться соответственно отрезками FМ и МN. Согласно определению параболы, можем написать:
Применяя формулу расстояния между двумя точками и приняв во внимание, что точка N имеет координаты 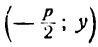
Заменив FМ и МN в равенстве (1) их выражениями, получим:
Это и есть уравнение параболы относительно выбранной системы координат, так как оно справедливо для любой ее точки.
Упростим уравнение (2). Для этого возведем обе части его в квадрат:
Приведя подобные члены, получим простейшее уравнение параболы
*) Можно показать, что уравнение (3) равносильно уравнению (2). Величина р называется параметром параболы.
Исследование уравнения параболы
Из уравнения (3) найдем:
Исследуем уравнение (1) для выяснения геометрической формы нашей кривой, полагая р > 0.
I. Положим
Отсюда следует: парабола 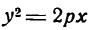
II. Если х 0, то у имеет два действительных значения, равных по абсолютной величине, но с разными знаками. Это значит, что каждому положительному значению х на параболе соответствуют две точки, расположенные симметрично относительно оси Ох.
Следовательно, парабола 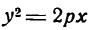
IV. Пусть х неограниченно возрастает, тогда и 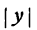
Итак, парабола 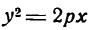
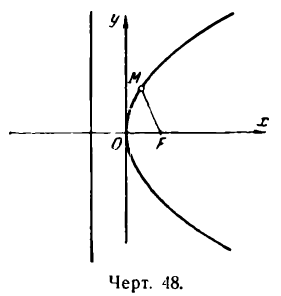
Вышеизложенное позволяет представить параболу, как показано на рис. 48.
Точка О называется вершиной параболы, отрезок FМ — фокальным радиусом точки М параболы, а бесконечная прямая Ох является ее осью симметрии.
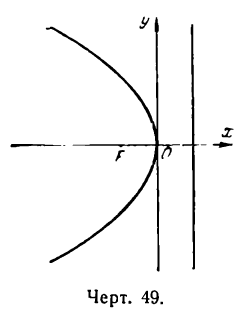
Если директрису параболы поместить справа от начала координат, то фокус и ветви ее расположатся как показано на рисеже 49.
При этом абсциссы точек параболы будут удовлетворять условию
а потому ее уравнение примет вид:
Парабола может быть симметрична и относительно оси Оу в этом случае фокус ее будет лежать па оси ординат, а директрисой будет прямая, параллельная оси Ох. Как видно при этом условии координатные оси поменяются ролями, и уравнение параболы примет вид
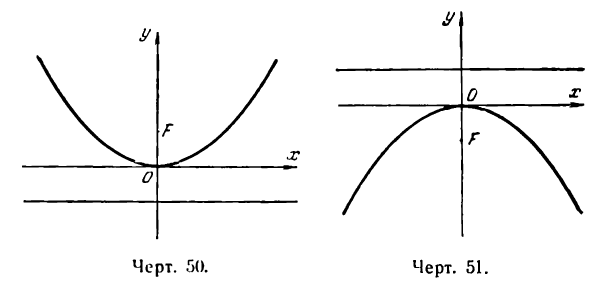
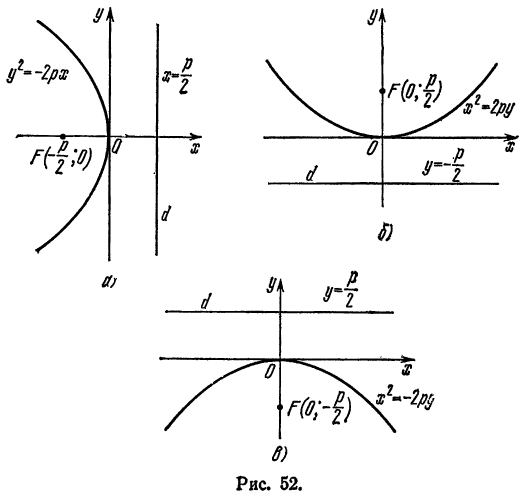
если ветви ее направлены вверх (рис. 50), и
если ветви направлены вниз (рис. 51).
Пример:
Найти координаты ее фокуса и написать уравнение директрисы.
Решение:
Данная парабола симметрична относительно оси Ох и расположена направо от оси Оу. Из уравнения находим:
Расстояние фокуса от начала координат равно 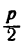
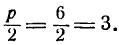
Директрисой служит прямая, параллельная оси Оу и отстоящая от последней на расстоянии 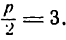
уравнение директрисы параболы будет х = — 3.
Пример:
Фокус параболы с вершиной в начале координат лежит в точке F(0; —4). Написать уравнение этой параболы.
Решение:
Согласно условию данная парабола симметрична относительно оси Оу, а ветви ее направлены вниз, поэтому искомое уравнение найдется из (3). Так как
и уравнение параболы будет:
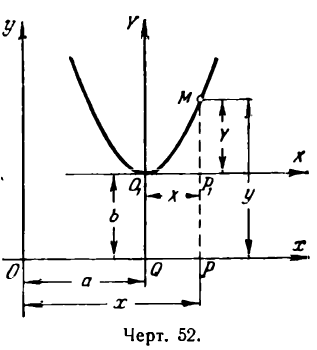
Уравнение параболы со смещенной вершиной и осью, параллельной оси Оу
Возьмем уравнения параболы (2) и (3) и запишем их в следующем виде:
Положив в уравнении (1)
Уравнение (2) определяет параболу, ветви которой направлены вверх, если А > О, вниз, если А
Возьмем на параболе произвольную точку М(х; у). Опустив из нее перпендикуляр МР на ось Ох, будем иметь:
Проведем через О1 прямые О1Х и QY, параллельные координатным осям Ох и Оу, и положим временно, что прямые О1Х и О1Y служат осями новой системы координат. Обозначим координаты точки М в этой системе через X и Y, т. е.
Уравнение параболы в новой системе координат напишется следующим образом:
Чтобы найти ее уравнение относительно прежних осей Ох и Оу, нужно X и Y выразить через х и y. Так как
Подставив в уравнение (3) найденные значения X и Y, получим:
Упростим уравнение (4); для этого раскроем в нем скобки.
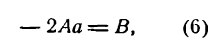
тогда уравнение (5) примет вид
Это—уравнение параболы с вершиной, лежащей в любой точке плоскости, и с осью симметрии, параллельной оси Оу.
Рассмотрим частные случаи.
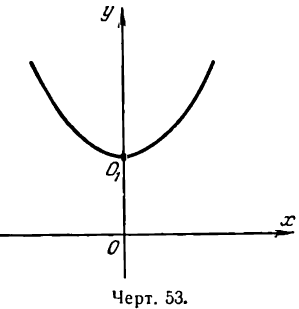
Пусть абсцисса вершины параболы a = 0; тогда величина В в равенстве (6) также будет нулем и уравнение (8) примет следующий вид:
Полученное уравнение определяет параболу, у которой вершина лежит на оси Оу, являющейся в то же время и ее осью симметрии (рис. 53).
Положим, что одна из точек параболы (исключая ее вершину) лежит в начале координат; тогда координаты (0; 0) должны удовлетворять уравнению (8). Заменив в нем х и у нулями, найдем С=0. В этом случае уравнение (8) получит вид
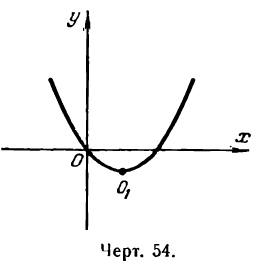
и будет определять параболу, проходящую через начало координат (рис. 54).
Заметим, что и уравнение (2) можно рассматривать как частный случай уравнения (8). Действительно, положив в равенствах (6) и (7)
вследствие чего уравнение (8) преобразуется в следующее:
Из сказанного следует, что парабола, у которой ось симметрии параллельна оси Оу или совпадает с ней, определяется уравнением
при любых значениях А, В и С, кроме А = 0.
Убедимся на примере, что справедливо и обратное утверждение: всякое уравнение вида (8) определяет параболу с осью симметрии, параллельной оси Оу.
Пусть дано уравнение
Преобразуем его следующим образом:
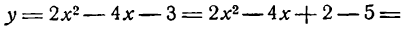
тогда уравнение (10) примет вид:
Уравнение (11) имеет такой же вид, как и уравнение (2), поэтому оно, а следовательно, и уравнение (9) определяют параболу, у которой ось симметрии параллельна оси Оу.
Для построения параболы, определяемой уравнением вида (8), можно использовать обычный прием, применяемый для вычерчивания графиков функций, а именно: дав х ряд значений, вычислить значения у, а затем, построив точки по найденным координатам, провести через них плавную линию.
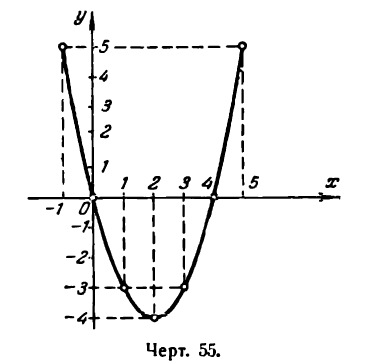
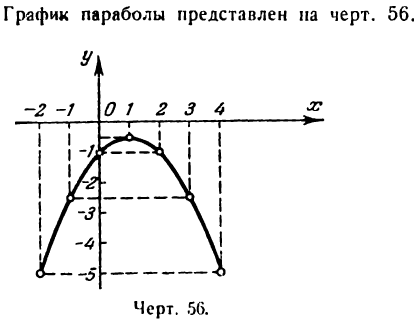
Пример:
Решение:
Прежде всего найдем абсциссы точек пересечения данной параболы с осью Ох; положив у = 0, получим:
Так как найденные точки симметричны относительно оси параболы, то вершина последней, находясь на этой оси, имеет 0 + 4 0
абсциссу, равную 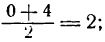
Этих трех точек достаточно для приближенного изображения параболы.
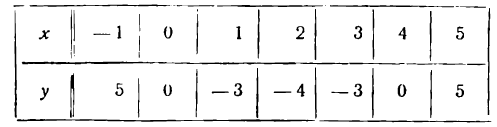
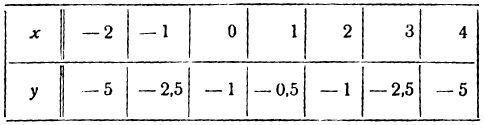
Для более точного ее представления нужны дополнительные точки. Составим следующую таблицу:
Построив эти точки и прозедя через них плавную линию, получим искомую параболу (рис. 55).
Пример:
Решение:
мнимые, а потому ось Ох не пересекает данную параболу. В этом случае следует найти абсциссы точек пересечения параболы с прямой
(-1 — свободный член данного уравнения параболы)
Решая для этой цели систему уравнений
Полученные точки симметричны относительно оси параболы, поэтому абсцисса ее вершины равна 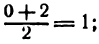
Присоединим к этим точкам несколько дополнительных точек. Составим таблицу:
Конические сечения
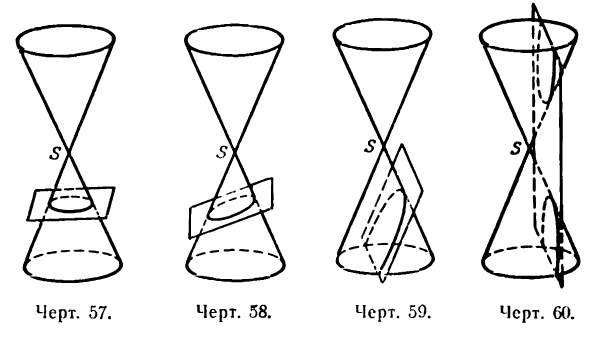
Окружность, эллипс, гипербола и парабола определяются, как мы установили в предыдущих лекциях уравнениями второй степени относительно текущих координат; поэтому их называют кривыми второго порядка. Они были известны еще древним грекам, которые изучали эти кривые, рассматривая их как результат сечения прямого кругового конуса плоскостью в следующих четырех случаях.
I. Секущая плоскость перпендикулярна к оси конуса; в сечении получается окружность (рис. 57).
II. Секущая плоскость образует с осью конуса угол, не равный 90°, и пересекает все его образующие по одну сторону от вершины S; в сечении получается эллипс (рис. 58).
III. Секущая плоскость параллельна какой-либо образующей конуса; при этом получается кривая, называемая параболой (рис. 59).
IV. Секущая плоскость пересекает обе полости конуса; при этом получаются две бесконечные ветви, образующие гиперболу (рис. 60).
Окружность, эллипс, гипербола и парабола называются коническими сечениями.
Конические сечения изучались в древности исключительно геометрическим путем, что представляло большие трудности, и только со времени Декарта, давшего метод координат, изучение их значительно упростилось.
Видео:7.1. Кривые второго порядка. Окружность. Эллипс. ГиперболаСкачать

Кривая второго порядка и её вычисление
Уравнение линии. Кривые второго порядка. Окружность. Эллипс. Гипербола. Парабола. Приведение к каноническому виду.
Уравнение линии в декартовых и полярных координатах
В лекции 3 было введено понятие неявной функции, задаваемой уравнением вида F(x,y) = 0.
Определение 6.1. Множество точек плоскости, координаты которых удовлетворяют некоторому уравнению
(6.1) F(x;y) = 0
называется линией (плоской кривой).
Не всякое уравнение определяет линию. Например, уравнение x² + y² = -1 не определяет никакой линии. Кроме того, линия может состоять из отдельных точек. Так, например, уравнению x² + y² = 0 удовлетворяет только начало координат.
Линия не обязательно является графиком функции. Так, например, уравнение x² + y² = 1 определяет окружность с центром в начале координат и радиуса 1 (т.к. d = 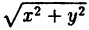
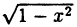
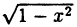
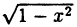
Уравнение произвольной окружности с центром в точке M(a;b) и радиусом R будет иметь вид:
(6.2) (х — а)² + (у- b)² = R²,
т.к. окружность радиусом R есть геометрическое место точек плоскости, находящихся на расстоянии R от центра, т.е. в соответствии с формулой ( 6.2) d = 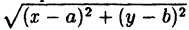
В частности, окружность с центром в начале координат, радиусом R, описывается уравнением
x² + y² = R².
Пример 6.1. Какую линию описывает уравнение x² + y² = Rx?
Решение: Перенося Rx в левую часть и выделяя полный квадрат, получаем:
x² + y² = Rx ⇔ X2 — Rx + у² = 0 ⇔ x² — Rx + 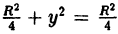
(х — 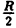
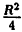
Ответ: данное уравнение описывает окружность с центром в точке M(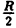
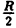
Линия может определяться на плоскости уравнением как в декартовых, так и в полярных координатах: F(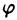




Пример 6.2. Построить график функции, заданной в полярных координатах уравнением r = 2 sin3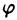

Решение: Составим таблицу некоторых значений этой функции:
 | 0 | 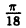 | 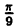 | 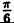 | 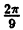 | 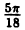 | 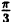 | 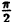 |
| r | 0 | 1 | 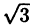 | 2 | 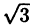 | 1 | 0 | -2 |
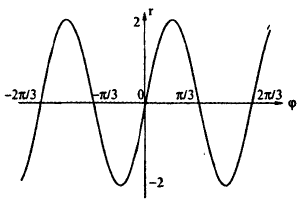
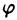
Далее, пользуясь тем, что из вида графика функции r = 2 sin 3

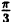
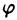
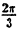

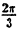
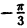

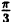
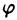
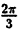
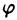
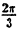
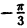

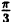
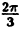
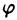
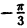
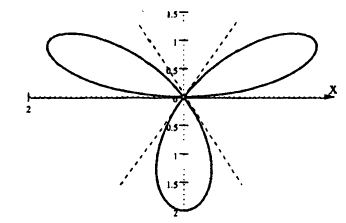

Такой график называют называют “трехлепестковая роза”.
Кривые второго порядка:
Определение 6.2. Кривой второго порядка называется линия, определяемая в декартовых координатах уравнением:
(6.3) Ax² + 2Bxy + Cy² + 2Dx + 2Ey + F = O.
Здесь коэффициенты — действительные числа и, по крайней мере, одно из чисел A₁B или C не равно нулю. Удобство таких обозначений для коэффициентов (2В, 2D, 2Е) станет ясно позже.
Всего существует три ’’реальных” кривых второго порядка: эллипс, (окружность — частный случай эллипса) гипербола и парабола, не считая такие линии, как ’’пара пересекающихся прямых” (ху = 0), «пара параллельных прямых” ((x — у)² — 4), ’’точка” ((x — 5)² + (у — 1)² = 0), ’’прямая” (х — 1)² = 0) и ’’мнимые кривые” (x² + y² + 5 = 0), которым не соответствует ни одна точка.
Окружность
Ранее было получено уравнение ( 6.2) окружности с центром в точке M(а; b), радиусом R. Это уравнение вида ( 6.3), т.е. окружность есть кривая второго порядка — можно показать, что уравнение (6.3), в котором A = C и B = O c помощью дополнения до полного квадрата каждой группы членов Ax² + 2Dx и By² + 2Еу приводится к виду (6.2), определяющему окружность радиуса R, или к виду: (х — а)² + (у — b)² = -R², не определяющему линию при R ≠ 0. Покажем это на примере.
Пример:
Показать, что уравнение 2x² + 2y² — 4x + 8y — 13 = 0 определяет окружность.
Решение: Поделив обе части на 2, получим уравнение в виде: x² + y² — 2x + 4y — 6,5 = 0 или, выделяя полный квадрат: (x² — 2х + 1) + (у² + 4y + 4) = 11,5 ⇔ (х — 1)² + (у + 2)² =11,5. Мы получим уравнение окружности с центром M(1; —2) и радиусом R = √11,5.
Пример:
Показать, что уравнение х² + у² + 6х — 6у + 22 = 0 не определяет никакой линии.
Решение:
Аналогично предыдущему, выделяя полный квадрат, получаем: х² + у² + 6х — 6у + 22 = 0 ⇔ (х² + 6х + 9) + (у² — 6у + 9) = — 4 ⇔ (x + 3)² + (y — 3)² =-4.
Эллипс
Определение:
Эллипсом называется множество всех точек плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, равна постоянной величине.
Обозначим фокусы F₁ и F₁, расстояние между ними 2с, а сумму расстояний до них от точек эллипса через 2а (2а > 2с). Выберем декартову систему координат как показано на рис. 72. По определению эллипса: MF₁ + MF₂ = 2а. Пользуясь формулой (2.6) получаем:
Обозначив b² = a² — с² > 0, получаем: b²x² + a²y² — a²b² или:
(6.4)
Уравнение ( 6.4) называется каноническим уравнением эллипса, а и b — полуосями, а — большая полуось, b — малая, т.к. b = 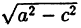
Так как 2а > 2с, то ε т.е. тем меньше эллипс вытянут вдоль фокальной оси Ох. В пределе, при ε → 0,a = b и получается окружность x² + у² = а² радиусом а При этом с = 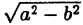
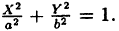
(6.5)
Гипербола
Определение 6.4. Гиперболой называется множество всех точек плоскости, модуль разности расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, равен постоянной величине.
Обозначим фокусы F₁ и F₂, расстояние между ними 2с, а модуль разности расстояний до них от точек гиперболы через 2a (2c > 2a > 0). Выберем декартову систему координат, как показано на рис. 72. По определению гиперболы: MF₁ — MF₂ = ±2а. Пользуясь формулой (2.6), аналогично тому, как это было сделано для эллипса, получаем:
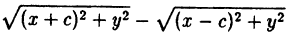
Уравнение (6.6) называется каноническим уравнением гиперболы, а и b — полуосями, а — действительной полуосью, b — мнимой. Так как х и у входят в уравнение только в четных степенях, гипербола симметрична относительно осей Ox и Оу. Выразив у из уравнения ( 6.6), получаем: 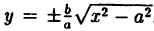
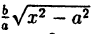
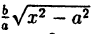
Точки пересечения гиперболы с осью Ox (фокальной осью) называются ее вершинами A₂(а;0), A₁(-a;0). C осью ординат гипербола не пересекается, поэтому фокальная ось называется действительной осью (а — действительная полуось), а перпендикулярная ей ось — мнимой осью (b — мнимая полуось). Можно показать, что при неограниченном возрастании абсциссы точка гиперболы неограниченно приближается к прямой у = 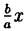
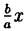
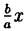
Отношение 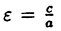
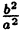
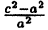
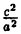
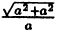
(6.7)
Уравнение асимптот такой гиперболы будет: у — y₀ =
Парабола
Определение:
Параболой называется множество всех точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой d, называемой директрисой (F ∉ d).
Обозначим расстояние от фокуса до директрисы р. Эта величина называется параметром параболы. Выберем декартову систему координат как показано на рис. 75.
По определению параболы MF=MN. Из рис. 75. ясно, что:
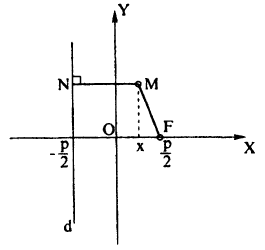
Приравнивая, получаем:
(6.8) у² = 2рх
Уравнение ( 6.8) называется каноническим уравнением параболы. Т.к. у входит в уравнение в четной степени, парабола симметрична относительно оси Ох. Выразив у из уравнения, получаем: у = 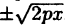
Ось симметрии параболы называется фокальной осью (ось Ox на рис. 76), точка пересечения пораболы с ней называется вершиной пораболы (точка О на рис. 76). Если вершина параболы находится в точке P(x₀; у₀), фокальная ось параллельна и одинаково направлена с осью Ox и расстояние от директрисы до фокуса равно Р, то с помощью параллельного переноса осей координат нетрудно получить уравнение такой параболы:
(6.9) (y — y₀)² = 2p(x -х₀)
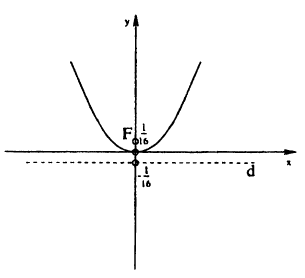
Пример:
Найти фокус, директрису, фокальную ось для параболы у= 4x².
Решение:
Как известно, осью симметрии параболы у = х² является ось Оу, а вершиной — точка О, поэтому фокальной осью будет ось Оу, вершиной — начало координат.
Для определения фокуса и директрисы запишем уравнение данной параболы в виде: x² = 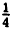
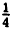
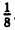
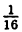
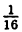
Понятие о приведении общего уравнения второго порядка к каноническому виду
Если в общем уравнении кривой второго порядка ( 6.3)
Ax² + 2Bxy + Cy² + 2Dx + 2Ey +F = 0
коэффициент 2B ≠ 0, то методами, которые будут изложены позже (лекция 34) это уравнение преобразуется к виду, в котором отсутствует член с произведением координат (т.е. 2В — 0).
Для приведения к каноническому виду уравнения ( 6.3), в котором 2В = 0, необходимо дополнить члены, содержащие х и у, до полных квадратов.
Если при этом (В = 0) А = С, то получится окружность (пример 6.3), точка или мнимая окружность (пример 6.4).
Если при этом (В = 0) A ≠ C и A ∙ C > 0, то получится эллипс (пример 6.8) или мнимый эллипс.
Если при этом (В = 0) A ≠ C и A ∙ C 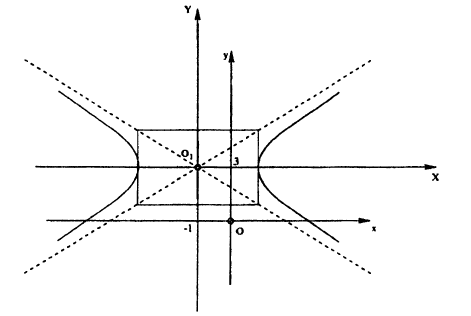
Пример:
Приведите к каноническому виду уравнение и определите вид кривой: x² — 6x — 4y + 29 = 0.
Решение:
Выделим полный квадрат: x² — 6x — 4y + 29 = 0 ⇔ x² — 6x + 9 = 4y — 20 ⇔ (x — 3)² = 4(у — 5). Сделав замену координат X =х — 3, Y = у — 5 мы получим каноническое уравнение параболы X² = 4Y с осью OY и параметром р = 2. Таким образом исходная парабола имела вершину A(3; 5) и ось х = 3 параллельную оси Oy (рис. 79).
Пример:
Приведите к каноническому виду уравнение и определите вид кривой: x² + 4y² + 2x — 24y + 21 =0.
Решение:
Выделив полный квадрат, получим уравнение: (x + 1)² + 4(у — 3)² = 16. Сделав замену координат: X = х + 1, Y = y — 3, получим каноническое уравнение эллипса: X² + AY² ⇔ 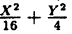
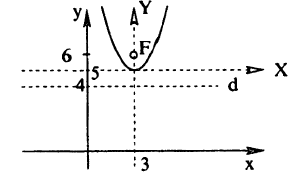
Видео:Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Решение заданий на тему: Кривые второго порядка
Пример:
Составьте уравнение окружности, имеющей центр 0(2; —5) и радиус R = 4.
Решение:
В соответствии с формулой (6.2) искомое уравнение имеет вид: (х — 2)² + (у + 5)² = 16.
Ответ: (х — 2)² + (у + 5)² = 16.
Пример:
Составьте уравнение эллипса, зная, что сумма полуосей равна 8 и расстояние между фокусами равно 8.
Решение:
Из условия имеем: a + b = 8, 2c = 8. C учетом того, что b² = а² — с², находим с = 4, а = 5, b = 3. Искомое уравнение эллипса будет: 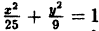
Ответ:
Пример:
Составьте уравнение гиперболы, зная, что фокусы F₁(10;0) и F₂(-10; 0) и что гипербола проходит через точку M(12; 3√5)
Решение:
Из условия имеем: с = 10, |MF₁ — MF₂|= 2а ⇔ 2а = 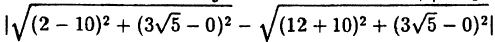
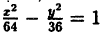
Ответ: 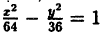
Пример:
Составьте уравнение параболы, зная, что фокус имеет координаты (5;0), а ось ординат является директрисой.
Решение:
Поскольку расстояние от директрисы параболы до ее полюса равно параметру р, а вершина находится на середине, из условия следует, что р = 5 и вершина расположена в точке A(2,5;0). Таким образом, в новых координатах X = х — 2,5; У = у каноническое уравнение параболы будет: Y² = 10Х, а в старых координатах: у² = 10(х — 2,5).
Ответ: y² = 10x — 25.
Пример:
Приведите к каноническому виду уравнение x² + y² — 2х + 6у — 5 = 0, определите вид кривой и ее параметры.
Решение:
Выделим полный квадрат: х² — 2х + у² + 6у — 5 = 0 ⇔ x² — 2x + 1 + у² + 6у + 9 — 1 — 9 — 5 = 0 ⇔ (х — 1)² + (у + 3)² = 15
В соответствии с формулой (6.2) это есть уравнение окружности с центром в точке A(1; -3), радиусом √5.
Ответ: (х — 1)² + (у + 3)² = 15.
Пример:
Приведите к каноническому виду уравнение x² + 4у² + 4х — 16у — 8 = 0, определите вид кривой и ее параметры:
Решение:
Выделим полный квадрат: x² + 4х + 4у² — 16y -8 = 0 ⇔ x²+4x + 4 + 4y²- 16y + 16-4-16-8 = 0 ⇔ (x + 2)² + 4(y²-4у+ 4) -28 ⇔ (х + 2)² + 4(y — 2)² = 28 ⇔ 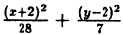
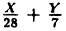
Ответ: 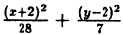
Пример:
Приведите к каноническому виду уравнение x² + 2y² + 8x — 4 = 0, определите вид кривой и ее параметры.
Решение:
Выделим полный квадрат:
x²+2y²+8x-4 = 0 ⇔ x²+8x+16+2y²-16-4 =0 ⇔ (x+4)²+2y2-20 = 0 ⇔ 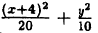
Сделав замену координат X = х + 4, Y — у, убеждаемся, что эта кривая — эллипс, с полуосями a = 2√5 и b = √10 и центром A(-4;0).
Ответ: 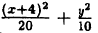
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
🌟 Видео
Аналитическая геометрия: окружность и эллипсСкачать
Кривые второго порядкаСкачать

Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать

Алгебра и геометрия 9. Эллипс. Гипербола. ПараболаСкачать

Лекция 31.3. Кривые второго порядка. Парабола.Скачать

Графики функций|Парабола, прямая и гиперболаСкачать
























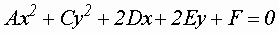
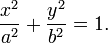 ,где
,где 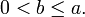
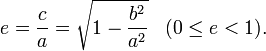 . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
. Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.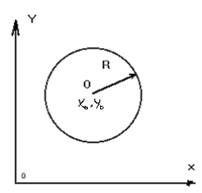 Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой её центром, на заданное ненулевое расстояние, называемое её радиусом.
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой её центром, на заданное ненулевое расстояние, называемое её радиусом.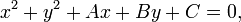
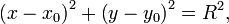
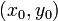 — центр окружности, R — её радиус.
— центр окружности, R — её радиус.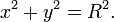
 Каноническое уравнение параболы в прямоугольной системе координат:
Каноническое уравнение параболы в прямоугольной системе координат: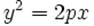 (или
(или 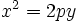 , если поменять местами оси)
, если поменять местами оси)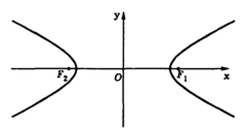 Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением :
Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением :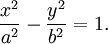
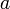 и
и 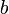 называются соответственно вещественной и мнимой полуосями гиперболы.
называются соответственно вещественной и мнимой полуосями гиперболы.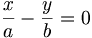 и
и 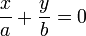 .
. .
. ..
..
 определяется уравнением первой степени относительно переменных
определяется уравнением первой степени относительно переменных  и
и 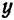 ;
;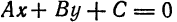 в прямоугольной системе координат определяет прямую и притом единственную.
в прямоугольной системе координат определяет прямую и притом единственную.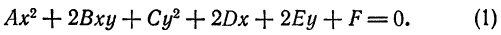
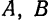 и
и 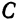 нулю (в противном случае уравнение (1) не будет уравнением второй степени).
нулю (в противном случае уравнение (1) не будет уравнением второй степени).

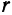 с центром в точке
с центром в точке 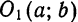 требуется составить ее уравнение.
требуется составить ее уравнение.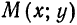
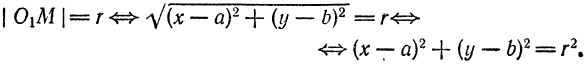
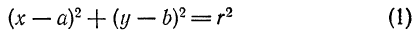
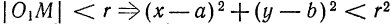 и
и 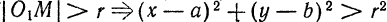 . Следовательно, (I) есть уравнение окружности радиуса
. Следовательно, (I) есть уравнение окружности радиуса 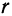 с центром в точке
с центром в точке 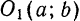 . Если центр окружности находится на оси
. Если центр окружности находится на оси 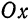 , т. е. если
, т. е. если 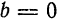 , то уравнение (I) примет вид
, то уравнение (I) примет вид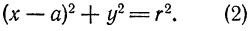
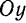 т. е. если
т. е. если 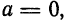 то уравнение (I) примет вид
то уравнение (I) примет вид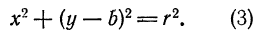
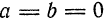 , то уравнение (I) примет вид
, то уравнение (I) примет вид
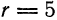 с центром в точке
с центром в точке 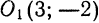 .
.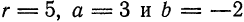 . Подставив эти значения в уравнение (I), найдем
. Подставив эти значения в уравнение (I), найдем 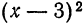
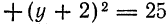 .
.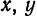
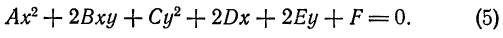
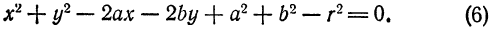
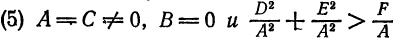 , то Уравнение (5) определяет окружность.
, то Уравнение (5) определяет окружность.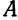 , получим:
, получим: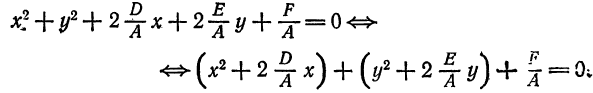
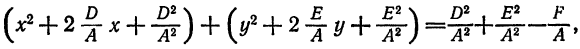
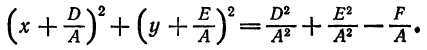
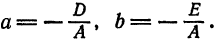 Так как, по условию,
Так как, по условию, 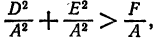 то можно положить
то можно положить 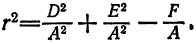
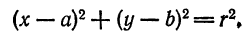
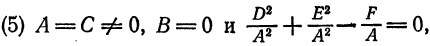 то оно определяет точку
то оно определяет точку 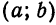 (говорят также, что окружность вырождается в точку). Если же
(говорят также, что окружность вырождается в точку). Если же 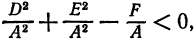 то уравнению (5) не удовлетворяет ни одна пара действительных чисел (говорят также, что уравнение (5) определяет «мнимую» окружность).
то уравнению (5) не удовлетворяет ни одна пара действительных чисел (говорят также, что уравнение (5) определяет «мнимую» окружность).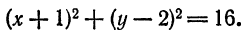
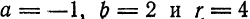 . Следовательно,
. Следовательно, 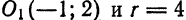 .
.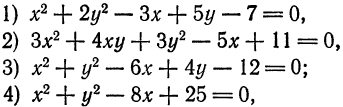
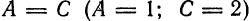 . Во втором уравнении
. Во втором уравнении 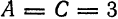 . Однако и оно не определяет окружность, потому что
. Однако и оно не определяет окружность, потому что 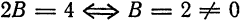 . В третьем уравнении условия
. В третьем уравнении условия 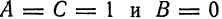 выполняются. Для окончательного вывода преобразуем его так:
выполняются. Для окончательного вывода преобразуем его так: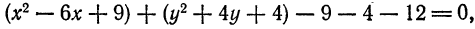
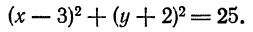
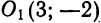 и радиусом
и радиусом 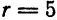 .
.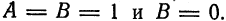 Однако преобразовав его к виду
Однако преобразовав его к виду 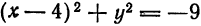 , устанавливаем, что оно не определяет никакой линии.
, устанавливаем, что оно не определяет никакой линии. и
и  которого лежат на оси
которого лежат на оси  и находятся на одинаковом расстоянии от
и находятся на одинаковом расстоянии от 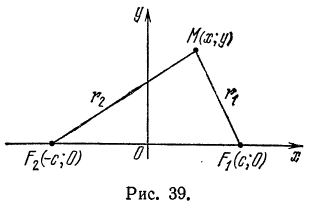
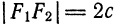 , получим
, получим 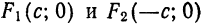 Пусть
Пусть 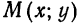 произвольная точка эллипса. Расстояния
произвольная точка эллипса. Расстояния 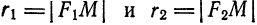 называются фокальными радиусами точки
называются фокальными радиусами точки 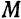 . Положим
. Положим
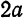 — величина постоянная и
— величина постоянная и 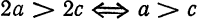 По формуле расстояния между двумя точками находим:
По формуле расстояния между двумя точками находим: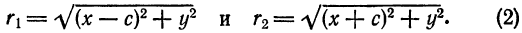
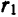 и
и  в равенство (1), получим уравнение эллипса:
в равенство (1), получим уравнение эллипса: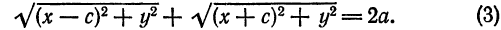
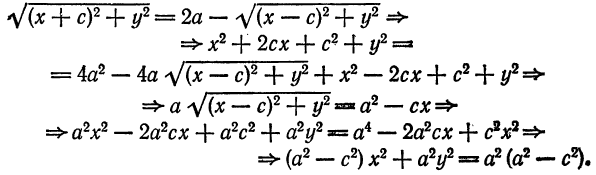
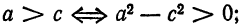 положим
положим
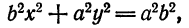

 и
и  любой точки
любой точки 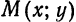 удовлетворяют уравнению (5) то она принадлежит эллипсу.
удовлетворяют уравнению (5) то она принадлежит эллипсу.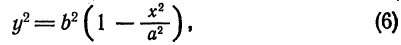
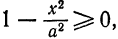 откуда
откуда
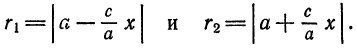
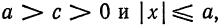 то
то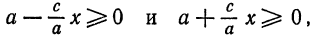
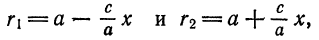
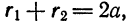

 не удовлетворяют уравнению (1), поэтому эллипс, определяемый этим уравнением не проходит через начало координат.
не удовлетворяют уравнению (1), поэтому эллипс, определяемый этим уравнением не проходит через начало координат.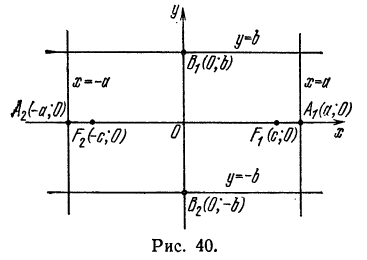
 , найдем
, найдем  Следовательно, эллипс пересекает ось
Следовательно, эллипс пересекает ось 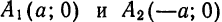 . Положив в уравнении (1)
. Положив в уравнении (1)  , найдем точки пересечения эллипса с осью
, найдем точки пересечения эллипса с осью  :
: 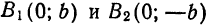 (рис.40).
(рис.40).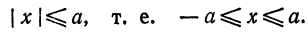
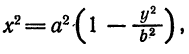
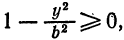 откуда
откуда 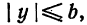 или
или 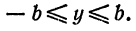
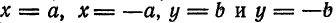
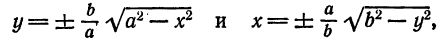
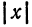 от 0 до
от 0 до 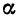 величина
величина 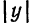 убывает от
убывает от 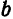 до 0, а при возрастании
до 0, а при возрастании 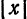 убывает от
убывает от 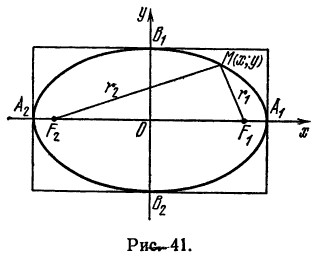
 пересечения эллипса с осями координат
пересечения эллипса с осями координат 
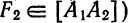 называется
называется 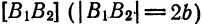 — малой осью. Оси
— малой осью. Оси 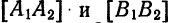 являются осями симметрии эллипса, а точка
являются осями симметрии эллипса, а точка  — центром симметрии (или просто центром) эллипса.
— центром симметрии (или просто центром) эллипса.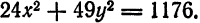
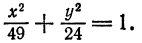
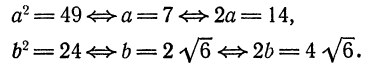
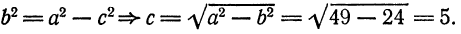
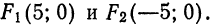
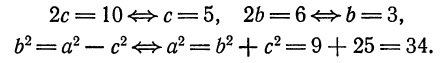
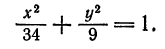
 Если же
Если же  то уравнение
то уравнение
 (рис. 42). В этом случае длина большой оси равна
(рис. 42). В этом случае длина большой оси равна 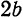 , а малой
, а малой 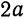 . Кроме того,
. Кроме того, 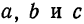 связаны между собой равенством
связаны между собой равенством
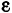 .
. , то, по определению,
, то, по определению,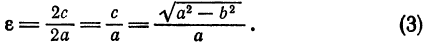
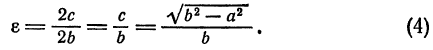
 . При этом с
. При этом с  и
и 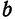 увеличивается соответствующим образом и эксцентриситет
увеличивается соответствующим образом и эксцентриситет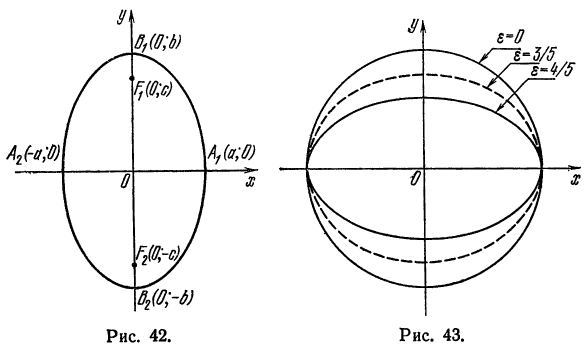
 и уравнение эллипса примет вид
и уравнение эллипса примет вид 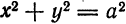 , которое определяет окружность с центром в начале координат. Таким образом, окружность можно рассматривать как частный случай эллипса, у которого полуоси равны между собой, а следовательно, эксцентриситет равен нулю.
, которое определяет окружность с центром в начале координат. Таким образом, окружность можно рассматривать как частный случай эллипса, у которого полуоси равны между собой, а следовательно, эксцентриситет равен нулю.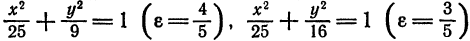 и окружность
и окружность 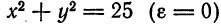 , хорошо видна зависимость формы эллипса от его эксцентриситета. В заключение поясним, как можно построить эллипс
, хорошо видна зависимость формы эллипса от его эксцентриситета. В заключение поясним, как можно построить эллипс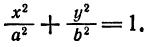
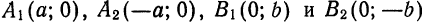 . Затем из вершины
. Затем из вершины 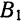 (можно из
(можно из 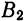 ) радиусом, равным а, на большой оси делаем засечки
) радиусом, равным а, на большой оси делаем засечки 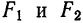 (рис. 44). Это будут фокусы эллипса, потому что
(рис. 44). Это будут фокусы эллипса, потому что 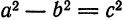 . Далее, берем нерастяжимую нить, длина которой равна
. Далее, берем нерастяжимую нить, длина которой равна 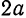 , и закрепляем ее концы в найденных фокусах. Натягиваем нить
, и закрепляем ее концы в найденных фокусах. Натягиваем нить
 По
По 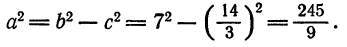
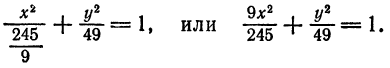

 лежат на оси
лежат на оси 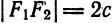 получим
получим 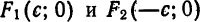 , Пусть
, Пусть  — произвольная точка гиперболы.
— произвольная точка гиперболы.
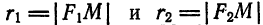 называются фокальными радиусами точки
называются фокальными радиусами точки 
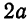 — величина постоянная и
— величина постоянная и 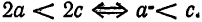 Подставив
Подставив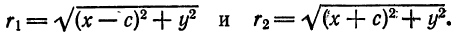
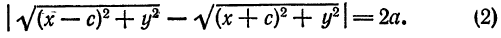
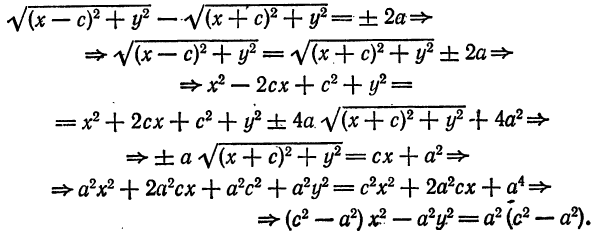
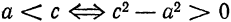 . Положим
. Положим
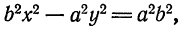

 удовлетворяют уравнению (4), то она принадлежит гиперболе.
удовлетворяют уравнению (4), то она принадлежит гиперболе.
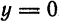 , найдем
, найдем 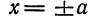 . Следовательно, гипербола пересекает ось
. Следовательно, гипербола пересекает ось 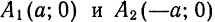 . Положив в уравнение (1)
. Положив в уравнение (1)  , получим
, получим 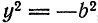 , а это означает, что система
, а это означает, что система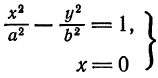
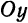 .
.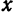 и
и 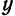 входят только в четных степенях, то гипербола симметрична относительно координатных осей, а следовательно, и относительно начала координат.
входят только в четных степенях, то гипербола симметрична относительно координатных осей, а следовательно, и относительно начала координат.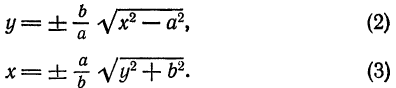
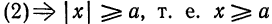 или
или 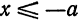 ; из (3) следует, что
; из (3) следует, что 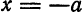 и справа от прямой
и справа от прямой 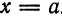
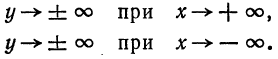
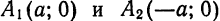 пересечения гиперболы с осью
пересечения гиперболы с осью  называются вершинами гиперболы. Отрезок Рис. 46.
называются вершинами гиперболы. Отрезок Рис. 46.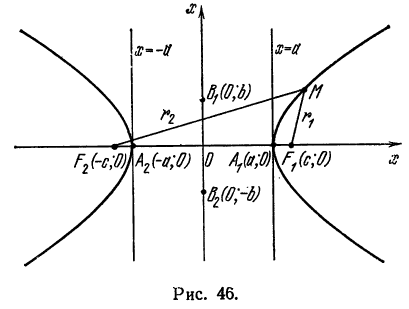
 ,
,  , называется мнимой осью. Число
, называется мнимой осью. Число  являются осями симметрии гиперболы. Точка
являются осями симметрии гиперболы. Точка 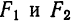 всегда находятся на действительной оси.
всегда находятся на действительной оси.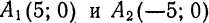 , а расстояние между фокусами равно 14.
, а расстояние между фокусами равно 14.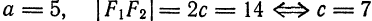 . По формуле
. По формуле 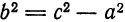 находим
находим 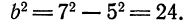
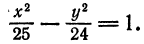
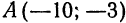 .
.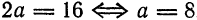 . Положив в уравнении (1)
. Положив в уравнении (1) 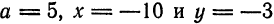 , получим
, получим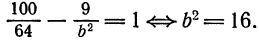
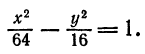
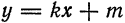 называется
называется 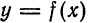 при
при 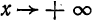 , если
, если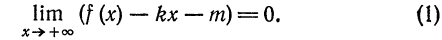
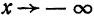 . Докажем, что прямые
. Докажем, что прямые

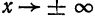
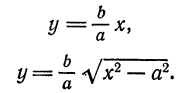
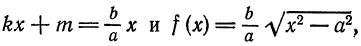 найдем:
найдем: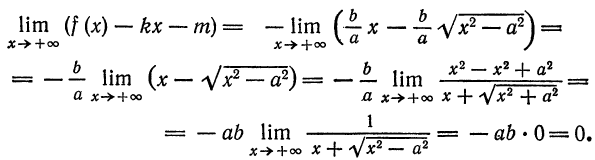
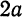 и
и  , а его центр находится в начале координат. При этом ветви гиперболы расположены внутри вертикальных углов,
, а его центр находится в начале координат. При этом ветви гиперболы расположены внутри вертикальных углов, 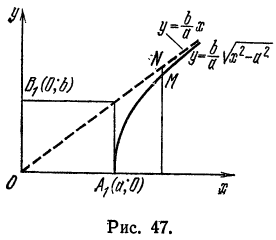
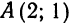 и, имеющей асимптоты
и, имеющей асимптоты 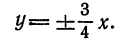
 и
и 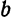 его найденным значением, получим:
его найденным значением, получим: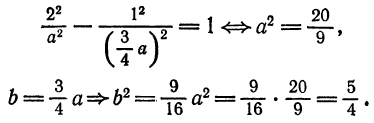
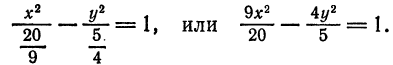
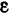 :
:
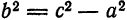 (§ 5) имеем
(§ 5) имеем 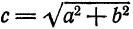 поэтому
поэтому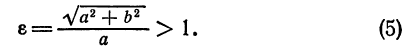
 .
.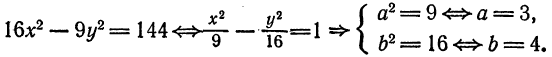
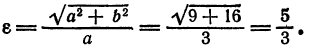
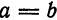 . В этом случае уравнение гиперболы принимает вид
. В этом случае уравнение гиперболы принимает вид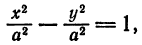

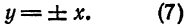
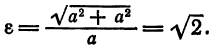
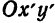 полученной в результате поворота осей старой системы вокруг начала координат на угол
полученной в результате поворота осей старой системы вокруг начала координат на угол 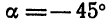 (рис.49).
(рис.49).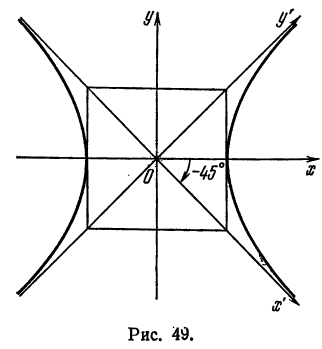
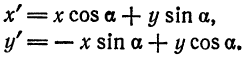
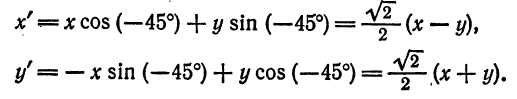
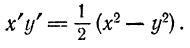

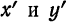 — величины обратно пропорциональные. Таким образом, равносторонняя гипербола, отнесенная к своим асимптотам, представляет собой график обратно пропорциональной зависимости.
— величины обратно пропорциональные. Таким образом, равносторонняя гипербола, отнесенная к своим асимптотам, представляет собой график обратно пропорциональной зависимости.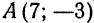 .
.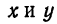 координатами точки
координатами точки 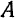 , получим:
, получим: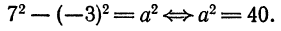

 которой лежит на оси
которой лежит на оси  , а
, а 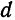 параллельна оси
параллельна оси 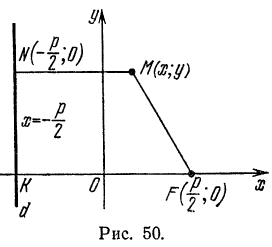
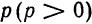 . Из рис. 50 видно, что
. Из рис. 50 видно, что 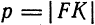 следовательно, фокус имеет координаты
следовательно, фокус имеет координаты 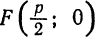 , а уравнение директрисы имеет вид
, а уравнение директрисы имеет вид 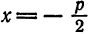 , или
, или 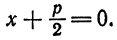
 — произвольная точка параболы. Соединим точки
— произвольная точка параболы. Соединим точки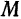 и
и 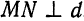 . Непосредственно из рис. 50 видно, что
. Непосредственно из рис. 50 видно, что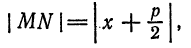
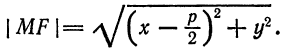

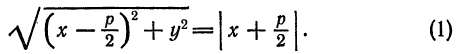
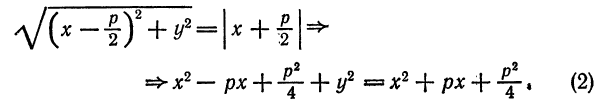

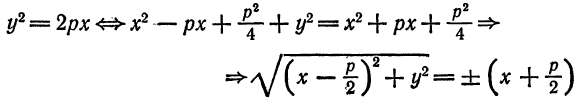
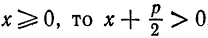 , и в левой части последнего уравнения можно оставить знак «плюс», т. е. оно является исходным уравнением параболы (1).
, и в левой части последнего уравнения можно оставить знак «плюс», т. е. оно является исходным уравнением параболы (1).
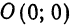 удовлетворяют уравнению (1), следовательно, парабола, определяемая этим уравнением, проходит через начало координат.
удовлетворяют уравнению (1), следовательно, парабола, определяемая этим уравнением, проходит через начало координат.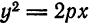 симметрична относительно оси абсцисс.
симметрична относительно оси абсцисс.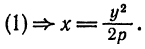
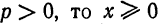 . Следовательно, парабола
. Следовательно, парабола 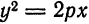 расположена справа от оси
расположена справа от оси 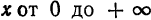 ордината
ордината 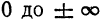 , т. е. точки параболы неограниченно удаляются как от оси
, т. е. точки параболы неограниченно удаляются как от оси 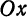 , так и от оси
, так и от оси  .
.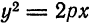 имеет форму, изображенную на рис. 51.
имеет форму, изображенную на рис. 51.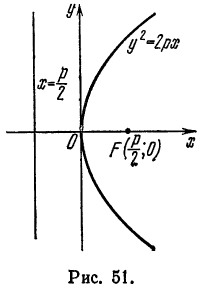
 является осью симметрии параболы. Точка
является осью симметрии параболы. Точка 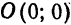 пересечения параболы с осью симметрии называется вершиной параболы. Отрезок
пересечения параболы с осью симметрии называется вершиной параболы. Отрезок 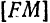 называется фокальным радиусом точки
называется фокальным радиусом точки 
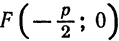 ; директриса
; директриса 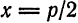 .
.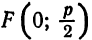 , а директриса
, а директриса  , то ветви параболы направлены вверх (рис. 52,6), а ее уравнение имеет вид
, то ветви параболы направлены вверх (рис. 52,6), а ее уравнение имеет вид
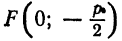 а директриса
а директриса 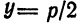 , то ветви параболы направлены вниз (рис. 52, в), а ее уравнение имеет вид
, то ветви параболы направлены вниз (рис. 52, в), а ее уравнение имеет вид
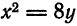 . Найти координаты ее фокуса и составить уравнение директрисы.
. Найти координаты ее фокуса и составить уравнение директрисы.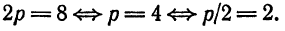
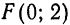 , а уравнение директрисы будет
, а уравнение директрисы будет 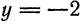 , или
, или 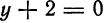 .
.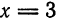 .
.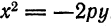 . Так как
. Так как 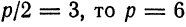 и, следовательно,
и, следовательно, 
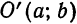 , ось симметрии которой параллельна оси
, ось симметрии которой параллельна оси 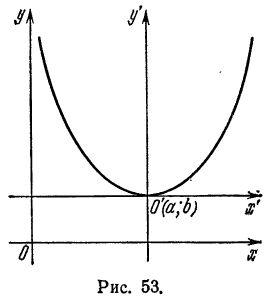
 . Относительно новой системы координат
. Относительно новой системы координат  парабола определяется уравнением
парабола определяется уравнением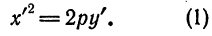

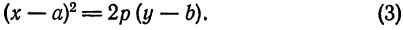
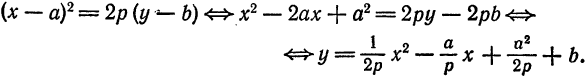
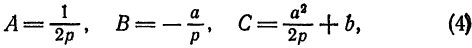
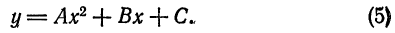
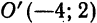 и с фокусом в точке
и с фокусом в точке 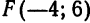 .
.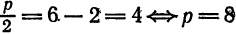
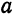 и
и 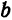 координатами точки
координатами точки 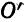 и
и 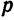 его найденным значением, получим:
его найденным значением, получим: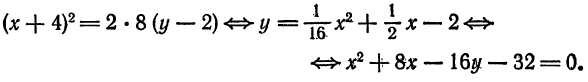
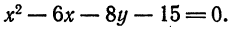
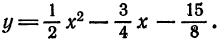
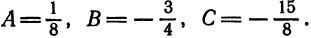 Из формул (4) имеем:
Из формул (4) имеем: 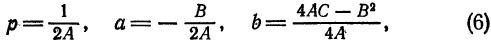
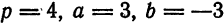 Подставляем найденные значения
Подставляем найденные значения 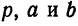 в уравнение (3):
в уравнение (3):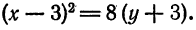
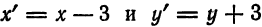 получим
получим 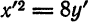 т. е, каноническое уравнение данной параболы.
т. е, каноническое уравнение данной параболы.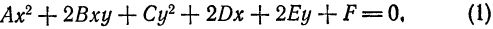
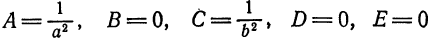 и
и 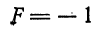 уравнение (1) примет вид
уравнение (1) примет вид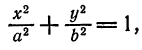
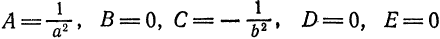 и
и 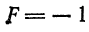 уравнение (1) примет вид
уравнение (1) примет вид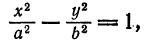
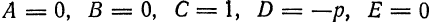 и
и  уравнение (1) примет вид
уравнение (1) примет вид 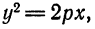 т. е. определяет параболу.
т. е. определяет параболу.
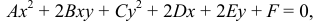
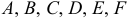 — действительные числа;
— действительные числа; 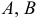 и
и 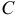 одновременно не равны нулю. Эта кривая называется кривой второго порядка.
одновременно не равны нулю. Эта кривая называется кривой второго порядка.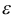 , является кривой 2-го порядка с эксцентриситетом, равным
, является кривой 2-го порядка с эксцентриситетом, равным 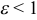 , то кривая второго порядка — эллипс;
, то кривая второго порядка — эллипс; 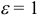 — парабола;
— парабола; 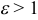 — гипербола.
— гипербола.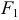 и
и 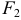 этой плоскости, называемых фокусами, есть величина постоянная, равная
этой плоскости, называемых фокусами, есть величина постоянная, равная 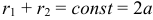 . Если фокусы совпадают, то эллипс представляет собой окружность.
. Если фокусы совпадают, то эллипс представляет собой окружность.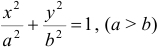 .
.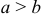 , то эллипс расположен вдоль оси
, то эллипс расположен вдоль оси 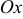 ; если
; если 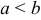 , то эллипс расположен вдоль оси
, то эллипс расположен вдоль оси 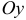 (рис. 9а, 9б).
(рис. 9а, 9б).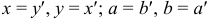 , перейдем в «штрихованную» систему координат, в которой уравнение будет иметь канонический вид:
, перейдем в «штрихованную» систему координат, в которой уравнение будет иметь канонический вид: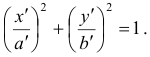
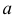 и
и 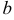 называются соответственно большой и малой полуосями эллипса.
называются соответственно большой и малой полуосями эллипса.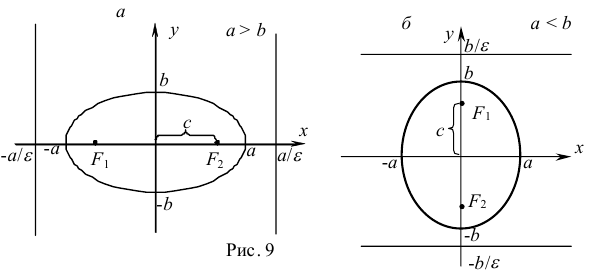
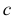 — расстояние от начала координат канонической системы координат до фокусов, то
— расстояние от начала координат канонической системы координат до фокусов, то 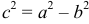 .
.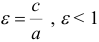 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.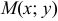 , лежащей на эллипсе, до каждого из фокусов является линейной функцией от ее абсциссы, т.е.
, лежащей на эллипсе, до каждого из фокусов является линейной функцией от ее абсциссы, т.е. 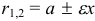 .
.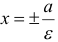 .
.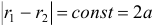 (рис. 10).
(рис. 10).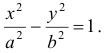
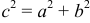 .
.
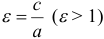 называется эксцентриситетом гиперболы.
называется эксцентриситетом гиперболы.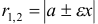 .
.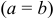 называется равносторонней.
называется равносторонней.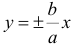 в канонической системе называются асимптотами гиперболы.
в канонической системе называются асимптотами гиперболы. этой плоскости равно расстоянию до некоторой фиксированной прямой, также расположенной в рассматриваемой плоскости (рис. 11).
этой плоскости равно расстоянию до некоторой фиксированной прямой, также расположенной в рассматриваемой плоскости (рис. 11).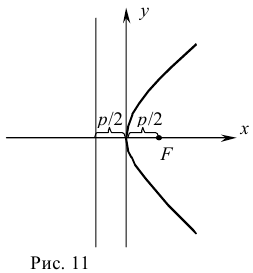
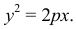
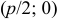 .
.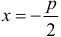 в канонической системе координат.
в канонической системе координат.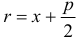 .
.
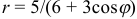 в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от
в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от 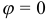 до
до 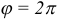 и придавая значения через промежуток
и придавая значения через промежуток 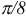 ; 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс — с полярной осью, привести его к каноническому виду; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.
; 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс — с полярной осью, привести его к каноническому виду; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.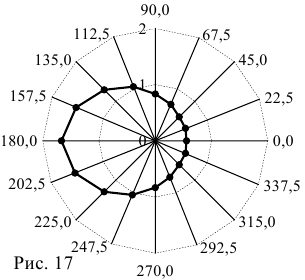
 с точностью до сотых при указанных значениях
с точностью до сотых при указанных значениях  , получим таблицу:
, получим таблицу:
 из полярной в декартовую систему координат, получим:
из полярной в декартовую систему координат, получим: 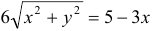 .
.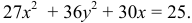 Выделим полный квадрат и приведем к каноническому виду:
Выделим полный квадрат и приведем к каноническому виду: 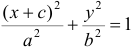 , где
, где 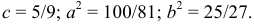
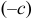 вдоль оси
вдоль оси 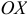 .
.