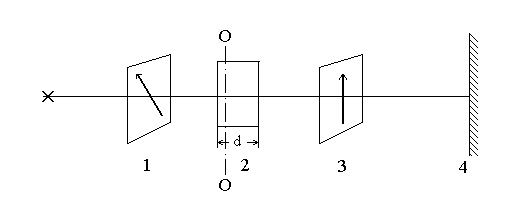
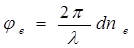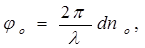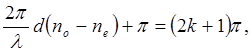Разность фаз колебаний вектора е двух когерентных лучей (8 видео)

Интерференция поляризованных лучей

Интерференцию поляризованных лучей можно наблюдать на следующей установке (рис. 1),

где: 1 — поляризатор; 2 -одноосный кристалл, оптическая ось ОО которого параллельна плоскости пластинки; 3 — анализатор; 4 — экран.

Параллельный пучок естественного света, направленный на поляризатор 1, превращаясь в линейно-поляризованный, падает на кристалл 2 перпендикулярно его поверхности. При нормальном падении пучка лучей на одноосный кристалл, оптическая ось в котором параллельна преломляющей поверхности, возникают два луча е и о. Эти лучи, обыкновенный и необыкновенный будут распространяться в одном направлении, но с разными скоростями. Лучи, обыкновенный и необыкновенный, созданные линейно-поляризованным светом, являются когерентными, а пройдя анализатор будут иметь колебания векторов Е_о и Е_е в одной плоскости.

Различие в скоростях обыкновенного и необыкновенного лучей внутри кристалла 2 приводит к возникновению некоторой разности фаз, а, следовательно, к оптической разности хода между двумя когерентными лучами. Таким образом, вышедшие из анализатора два луча удовлетворяют всем условиям, необходимым для осуществления интерференции.

а) Рассмотрим случай, когда плоскости поляризатора П и анализатора А ориентированы параллельно друг другу.

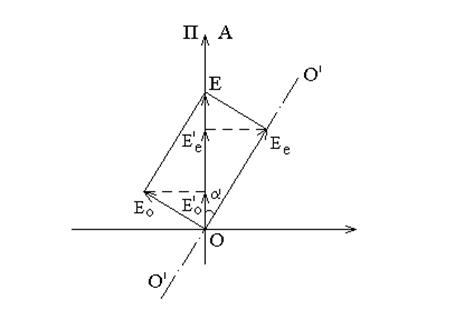
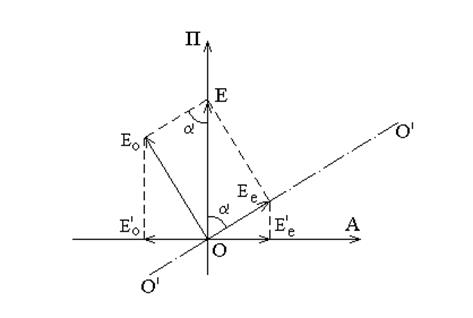
Этому случаю соответствует векторная диаграмма, представленная на рис.2.

Здесь П и А – направления, вдоль которых совершаются световые колебания вектора Е в поляризаторе П и анализаторе А. О’О’ — оптическая ось вещества, обладающего двойным лучепреломлением.

Световой луч входит в вещество в точке О перпендикулярно листу с направлением колебания электрического вектора Е, указанного на рис. 2. В анизотропном веществе он разбивается на Е₀ и Е_е, анализатор пропустит лишь составляющие Е¢₀ и Е¢_е.

Если угол между поляризатором (вектором Е) и осью вещества (кристалла) обозначить через α, то составляющие амплитудных значений векторов Е₀ и Е_е, пропущенные анализатором А, будут иметь значения:

Мы видим, что оба вектора Е¢₀ и Е_е‘ направлены в одну сторону, но

При выходе из вещества оба луча приобретут соответственно дополнительные фазы

где n_e и n_о — показатели преломления необыкновенного и обыкновенного лучей; l — длина световой волны в вакууме; d — толщина вещества; dn_e или dn_о — оптический путь в веществе.

Тогда разность фаз, которую приобрели два луча по выходе из вещества, будет равна

. (2)

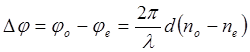
Если Dj = 2kp, где k = 1,2,3,…, то

, (3)

(4)

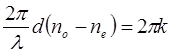
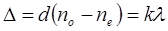
т.е. оптическая разность хода обыкновенного и необыкновенного лучей равна целому числу волн. Т.к. колебания Е₀¢ и Е_е¢ когерентны, то они интерферируют, в результате чего выходящий из анализатора свет будет иметь максимальную интенсивность. Свет остался линейно поляризованным, т.к. колебания Е₀¢ и Е_е¢ происходят вдоль направления оси анализатора.

Если Dj = (2k + 1)p, где k = 0,1,2,…, то

(5)

, (6)

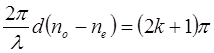
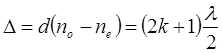
т.е. оптическая разность хода двух лучей будет равна нечетному числу полуволн. Происходит гашение, но не полное так как Е₀¢ ≠ Е¢_е. следовательно о и исходящий из анализатора свет будет меньшей интенсивности, происходит гашение, но не полное.

Сделанный вывод справедлив для любых значений угла a, кроме .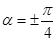

Таким образом, при любой толщине вещества, в случае параллельности осей поляризатора и анализатора, поле зрения окажется более или менее просветленным.

Если на пластинку направлять не монохроматический, а белый свет, то благодаря частичному гашению некоторых участков спектра прошедший свет уже будет не белым, а окрашенным.

б) Расположим теперь поляризатор и анализатор перпендикулярно друг другу.

Этому случаю соответствует векторная диаграмма, рассмотренная на рис.3.

Составляющие амплитудных значений векторов Е₀ и Е_е, пропущенных анализатором А, будут:

но они анализатором разведены в разные стороны. По выходе из вещества оба луча, как и в первом случае, приобретут дополнительную разность фаз

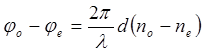
а при выходе из анализатора, еще дополнительную разность фаз p. Следовательно, по выходе из анализатора оба луча обыкновенный и необыкновенный, имеют добавочную разность фаз:

. (8)

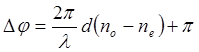
Максимумы интенсивности будут иметь место, когда Dj = 2kp, т.е.

, (9)

, (10)

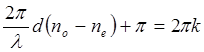
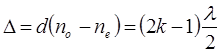
т.е. оптическая разность хода обыкновенного и необыкновенного лучей будет равна нечетному числу волн. Свет линейно поляризован.

Минимумы интенсивности будут соответствовать условию

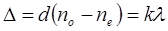
Так как Е₀¢ = Е_е¢, то гашение будет полным.

Таким образом, мы видим, что в этом случае картина интерференции является дополнительной к той, которая возникает при параллельности осей поляризатора и анализатора. Следовательно, дополнительными будут и окраски интерференционной картины для обоих ориентаций осей поляризатора и анализатора, если освещение производить белым светом.

Если толщина вещества d различна, то максимумы и минимумы проходящего света будут иметь место для соответствующих толщин. Поэтому при освещении белым светом пластинок разной толщины вырезанных из кристалла будет наблюдаться разная окраска этих пластинок.

Дата добавления: 2015-04-29 ; просмотров: 1253 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Волны Основные понятия.Интерференция.Разность хода.Условие максимума и минимумаСкачать

Разность ходаи разность фаз.

Интерференция двух лучей. Принцип получения интерференционной картины. условия максимумов и минимумов. Разность фаз и разность хода. Примеры: а) Интерференция в тонкой пленке; б) кольца Ньютона. Применение интерференции света.

1. Получение интерференционной картины

В 1803г. английский физик Т.Юнг с помощью двух щелей получил на экране интерференционную картину. Его опыт заключался в следующем: источником света служила ярко освещенная щельS, от которой световая волна падала на две узкие равноудаленные щели S₁ и S₂, параллельные S (рис. 2.2). Щели S₁ и S₂ можно считать когерентными источниками света, а все три упомянутые щели можно рассматривать как точечные источники, свет от которых распространяется во всех направлениях. Волны, идущие от S₁ и S₂, накладываясь друг на друга, интерферируют. Интерференционная картина наблюдается на экране Э (рис. 2.2).

Обозначим расстояние между щелями S₁ и S₂ равным d, а между щелями и экраном — l, причем l » d (рис. 2.3 а). Точка О – центр экрана, она расположена симметрично относительно щелей S₁ и S₂. Результат интерференции волн в произвольной точке экрана М, находящейся на расстоянии х от его центра О, должен определяться разностью хода Δ = l₂— l₁. Математический расчет дает для разности хода Δ = хd/l. В тех местах экрана, которые удовлетворяют условию , образуется интерференционный максимум. Отсюда

В тех местах экрана, где , волны “гасят” друг друга и образуется интерференционный минимум. Отсюда

Шириной интерференционной полосы Δх называется расстояние между соседними максимумами или минимумами

Величина Δх постоянна при заданных d, l и λ и не зависит от порядка интерференции m. Таким образом, при освещении щелей монохроматическим светом на экране наблюдается чередование светлых и темных полос одинаковой ширины (рис. 2.3 б). Чтобы полосы были хорошо различимы, Δхдолжна быть порядка 5 мм, тогда при λ = 500 нм отношение l/d равно 10000, т.е. выполняется условие l » d.

При освещении щелей белым светом интерференционные максимумы становятся радужными. Это происходит из-за того, что положение интерференционного максимума зависит от длины волны падающего света, а белый свет содержит в себе все цвета спектра. Максимумы коротких длин волн (фиолетовых) будут располагаться ближе к центру экрана, за ними следуют максимумы синих длин волн и т.д. до самых длинных красных (рис. 2.3 в). В середине экрана при m = 0 максимумы всех волн совпадут из-за отсутствия разности хода и получится белая полоса.

2.Условия максимума и минимума интерференции

При сложении двух колебаний амплитуда результирующего колебания зависит от разности фаз складываемых колебаний:

, (1)

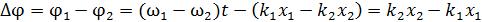
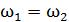
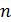
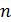
так как . Здесь – волновое число; длина волны зависит от показателя преломления среды, в которой распространяется волна; величина в раз меньше, чем длина волны в вакууме:

. (2)

С учетом этого соотношения разность фаз колебаний светового вектора двух волн в точке наблюдения , согласно формуле (1):

(3)

Здесь – оптическая разность хода волн; – оптическая длина пути; это произведение геометрического пути волны (от источника света до точки наблюдения) на показатель преломления среды, в которой это расстояние пройдено.

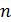
Условие максимумов интенсивности света в точке наблюдения :

(4)

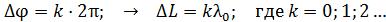
т. е. колебания световых векторов двух волн 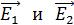в точке происходят в одинаковой фазе, при этом в любой момент времени .

Условие минимумов интенсивности света в точке :

; … (5)

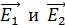
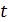
т. е. колебания складываемых световых векторов в точке происходят в противофазе, при этом в любой момент времени .

Отметим, что при сложении двух колебаний на векторной диаграмме (где колебание изображают вращающимся вектором амплитуды ) разность фаз колебаний – это угол между векторами , а амплитуда результирующего колебания (равна сумме векторов амплитуд). Условию максимумов интенсивности (4) соответствует рис. 6 а, а условию минимумов (5)

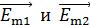
Разность ходаи разность фаз.

Разность хода

Изменению разности фаз на соответствует изменение разности хода на .

В вакууме оптическая разность хода в отличие от разности фаз имеет наглядную интерпретацию. Если две интерферирующие волны испускаются одним источником света, то разность хода — это геометрическая разность длин путей, по которым два интерферирующих луча от одной точки источника достигли одной точки экрана.

Например, в оптической схеме опыта Юнга, изображенной на рис. 18, разность хода для точки P на экране находится по формуле:

В изотропной среде скорость света в раз меньше, чем в вакууме, здесь — показатель преломления среды. Частота света в среде и в вакууме одинакова, поэтому длина волны в среде в раз меньше. В соответствии с соотношением вместо реального уменьшения длины волны можно рассматривать неизменную и соответствующее увеличение длины пути луча. С этой целью вводится понятие оптической длины пути, которая в раз больше геометрической длины. Далее, употребляя термин «разность хода», всегда будем иметь в виду оптическую разность хода.

Заменяя разность фаз интерферирующих волн оптической разностью хода, получаем следующее выражение для интенсивности интерференционной картины:

Приемники света в оптическом диапазоне реагируют на интенсивность света, а не на напряженность электрического или магнитного полей. Поэтому измеряемые в опыте величины, ширина полос и видность, также могут быть выражены через интенсивность, а значит и через оптическую разность хода. Следовательно, понятие оптической разности хода позволяет свести оптическую задачу по интерференции к геометрической задаче отыскания разности хода.

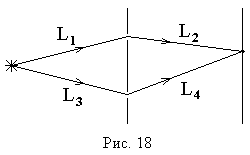
Отметим, что разность хода лучей можно отсчитывать не только как разность длин путей от источника до точки наблюдения, но и как разность длин путей от двух точек любой поверхности равной фазы волны до точки наблюдения. При этом, конечно, две точки на поверхности равной фазы — не произвольные точки, а должны быть точками, через которые реально проходят лучи, попадающие в точку наблюдения. Так на рис. 18 , поэтому две щели находятся на поверхности равной фазы, и, следовательно, разность хода можно найти по упрощенной формуле . Этот прием часто используется при решении задач.

Разность фаз

Графики двух периодических функций (колебаний) одинаковой частоты задержаны (сдвинуты) один относительно другого. Задержка во времени эквивалентна соответствующей разности фаз.

А).Интерференция в тонких пленках

Луч света длиной волны λ падает на пленку толщиной dпод углом падения i(рис. 4.6) и делится на два: луч 1 отражается от верхней грани, а луч 2 преломляется, проходит в пленка расстояние АВ, затем отражается от нижней грани, проходит расстояние ВС и затем преломляется. Два луча собираются линзой в одной точка, расположенной в фокальной плоскости линзы. Для расчета картины интерференции на экране найдем оптическую разность хода лучей 1 и 2.

Разность хода лучей 1 и 2 в точке Аравна нулю, так как они двигались вместе, составляя луч падающего на пластинку света. После линии ОС (она перпендикулярна лучам 1 и 2) их разность хода не изменяется, так как линза не дает дополнительной разности хода для этих лучей. Поэтому оптическая разность хода возникает при переходе лучей от точки А к линии ОС:

Рис. 4.6

Оптическим ходом луча называют произведение

геометрического хода (АВ +ВС) на показатель

преломления среды, в которой распространяется луч. На участке АО луч 1 распространяется в воздухе, для которого n_В = 1. В формулу для оптической разности хода введено слагаемое λ₀/2, так как вектор напряженности луча 1 при отражении от оптически более плотной среды изменяет свою фазу на π или луч 1 теряет полволны. λ₀ – длина волны в вакууме. Подставляя параметры пленки и угол падения в формулу (4.3), для оптической разности хода можно окончательно записать:

.(4.4)

Для данного примера условия наблюдения максимумов и минимумов будут выглядеть таким образом:

максимумы:

минимумы:

Отметим, что для наблюдения интерференционной картины нужно брать тонкую пленку, чтобы для естественного света лучи 1 и 2 после линии ОСбыликогерентными: ОС ≤ r_к (из за пространственной когерентности) и ∆ ≤ l_к (из за временной когерентности).

Как видно из формулы (4.4), оптическую разность хода лучей ∆ можно изменять либо изменением угла падения i, либо изменяя толщину пленки d. Рассмотрим полученные интерференционные картины.

Если на пленку одинаковой толщины d падает монохроматический свет под одним и тем же углом i и выполняется условие максимума, то пленка в отраженных лучах будет светлой (имеющий цвет падающей длины волны). При выполнении условия минимума отраженных лучей не будет. Свет не отражаясь, проходит через пленку.

Рис. 4.7

Если на пленку с линейно изменяющейся толщиной d (клин) (рис. 4.7) падает монохроматический свет под одним и тем же углом i, то в отраженных лучах будут наблюдаться полосы равной толщины. Если на этот клин направить белый свет, то максимумы превратятся в спектры.

В пределах каждого максимума цвет будет плавно меняться от красного к фиолетовому.

Б). Кольца Ньютона.

Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис.32.9). Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падении света имеющие вид концентрических окружностей.

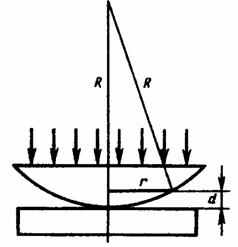
Рис.32.9. Схема наблюдения колец Ньютона.

В отраженном свете оптическая разность хода (с учетом потери полуволны при отражении), согласно (32.9), при условии, что показатель преломления воздуха n = 1, а i = 0,где d — ширина зазора. Из рис. 32.9 следует, чтоR2 = (R – d)2 + r2, где R — радиус кривизны линзы, r — радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая, что d мало, получим Следовательно, (32.12)Приравняв (32.12) к условиям максимума (32.3) и минимума (32.4), получим выражения для радиусов m-го светлого кольца и m-го темного кольца соответственно (m = 0,1,2. ), — светлое кольцо,

(m = 0,1,2,…) – темное кольцо.

Видео:Что такое когерентные волны? Душкин объяснитСкачать

Разность фаз колебаний вектора е двух когерентных лучей

Волновая оптика – круг явлений, в основе которых лежит волновая природа света.

Основными явлениями, которые рассматриваются в волновой оптике являются: интерференция, дифракция и поляризация света, а также законы и эффекты связанные с этими тремя явлениями.

Уравнение плоской электромагнитной волны, распространяющейся вдоль положительного направления оси X, имеет вид:

В электромагнитной волне колеблются два вектора напряженности электрического (E) и напряженности магнитного (H) полей. Вектор напряженности электрического поля E называют световым вектором, так как физиологическое, фотохимическое, фотоэлектрическое и др. действия света вызываются колебаниями электрического вектора.

Свет распространяется с различными скоростями. В различных средах свет распространяется с различными скоростями.

v=c/n, где c – скорость света в вакууме, v – скорость света в среде с показателем преломления n. Максвелл установил, что n=√εμ, где ε –диэлектрическая проницаемость, μ – магнитная проницаемость среды. Если вещество прозрачное и μ=1, то n=√ε . Диэлектрическая проницаемость зависит от частоты излучения, следовательно и показатель преломления зависит от частоты, т.е. скорость распространения электромагнитных волн зависит от частоты v=v(ν) или длины волны v=v(λ). Зависимость показателя преломления света (скорости света в среде) от длины волны носит название дисперсии света.

«Средний» человеческий глаз воспринимает излучение длиной волны от 0,4 мкм до 0,76мкм (в ангстремах от 4000 Å до 7600 Å). Длина волны в вакууме λ₀=c/ν, в среде λ = v/ν = c/νn = λ₀/n.

Частота видимого света:

ν = (0,39÷0,75)·10 15 Гц.

Принятое в настоящее время значение скорости света в вакууме