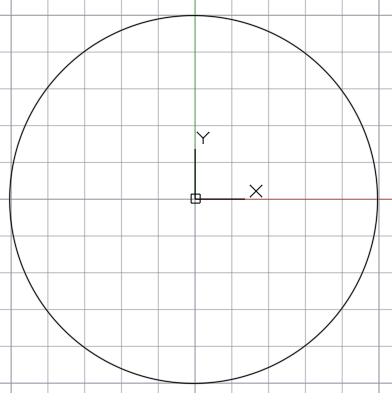
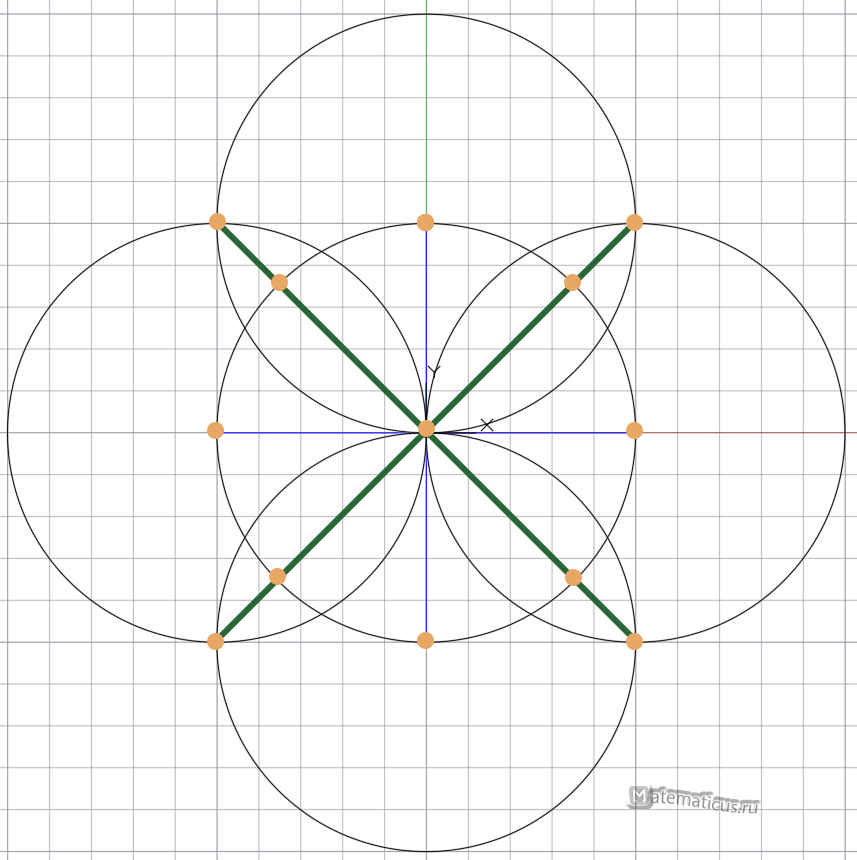
Чтобы разделить окружность на 8 равных частей чертим циркулем окружность (данная окружность условно будет исходной или первоначальной)
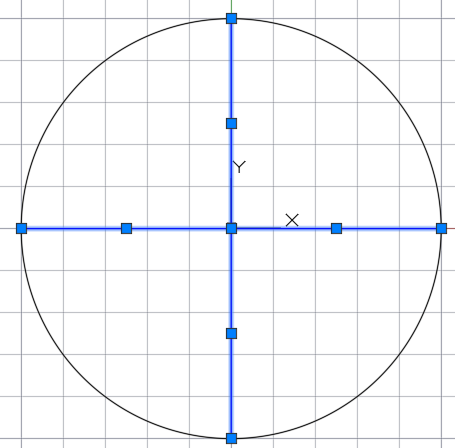
Далее проводим с помощью линейки две пары взаимно перпендикулярных диаметров окружности
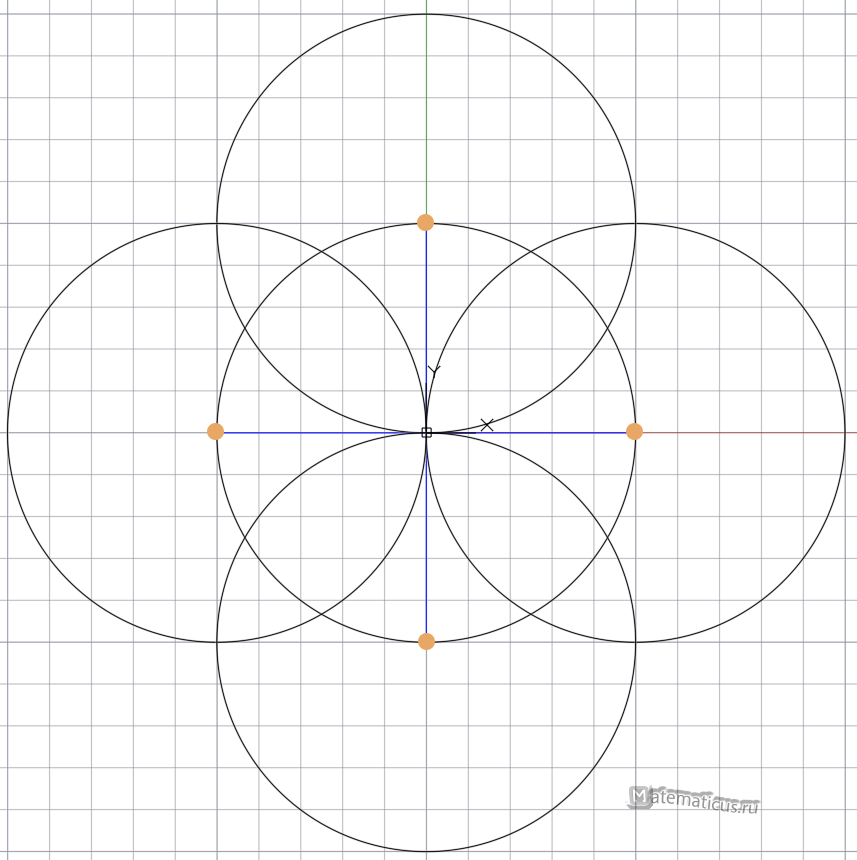
Затем с помощью циркуля чертим ещё четыре таких же окружности, где их центры находятся в точках окончания диаметров исходной окружности.
Далее отмечаем точки пересечения окружностей и к центру первоначальной окружности с помощью линейки чертим четыре взаимно симметричных отрезков
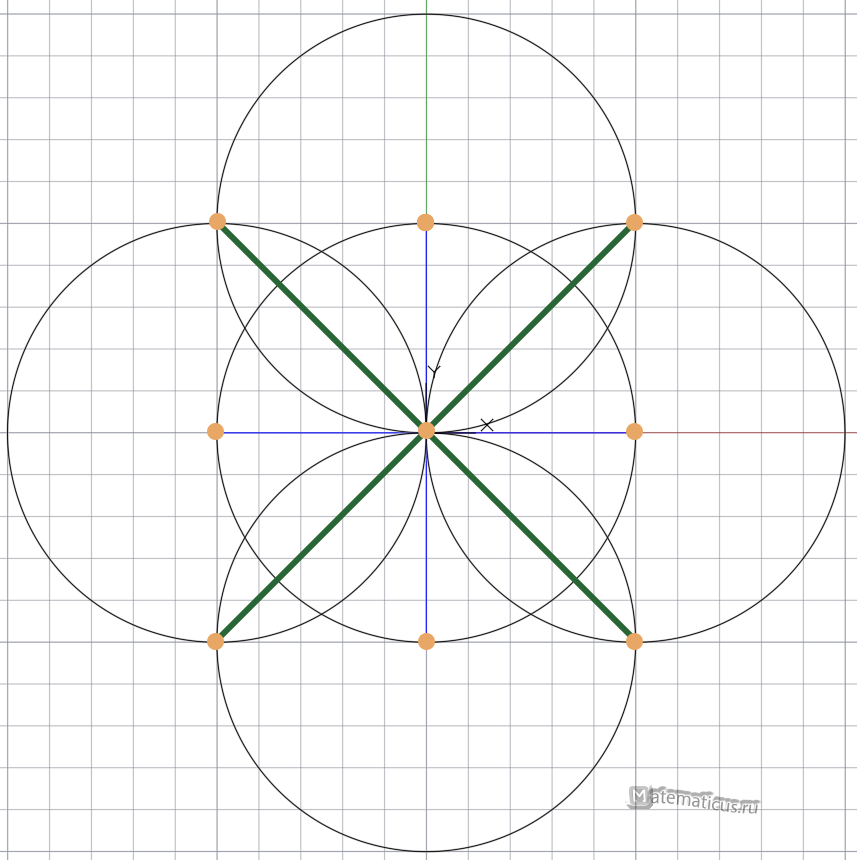
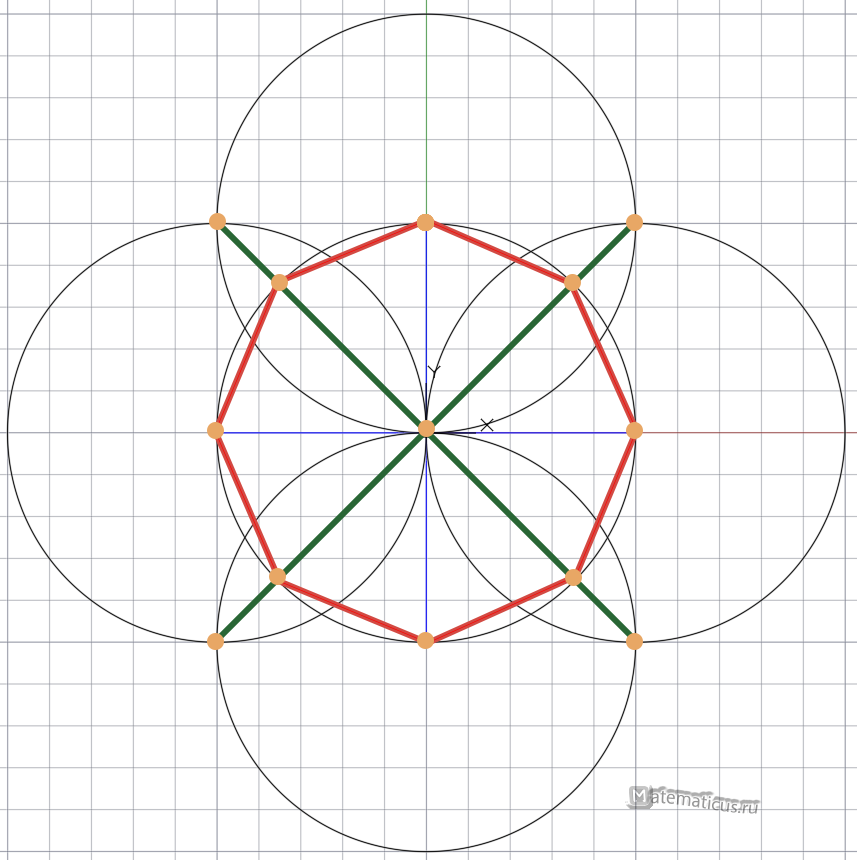
Отмечаем точки пересечения отрезков с исходной окружностью
Соединяем точки между собой (угол отрезков относительно диаметров первоначальной окружности составляет 45 0 ) и получаем правильный восьмиугольник — с равными сторонами
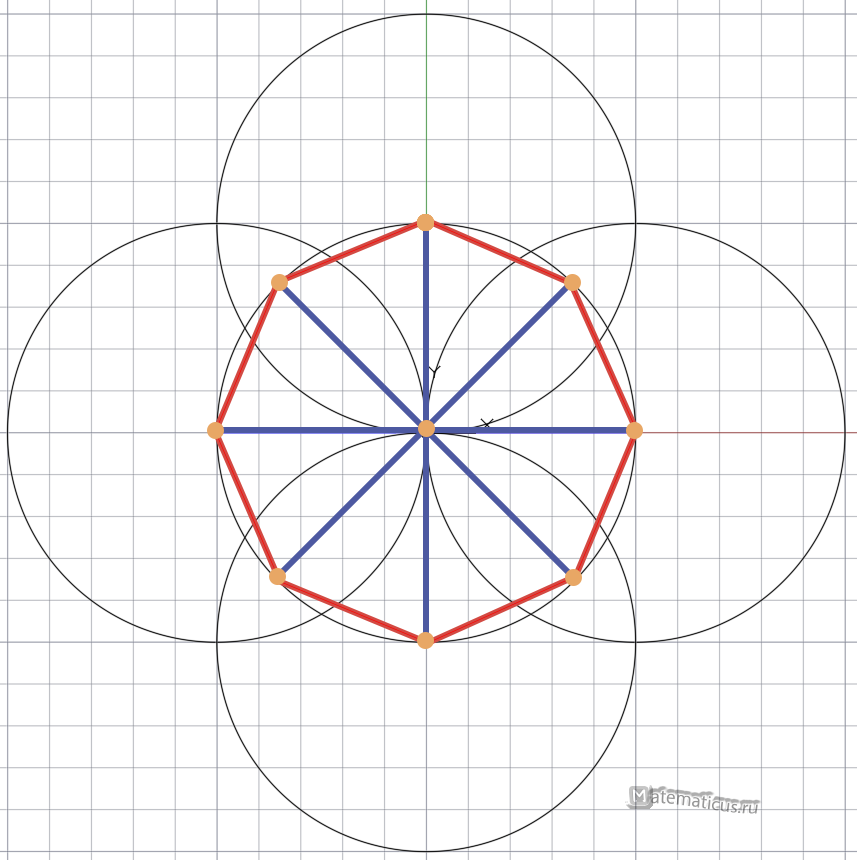
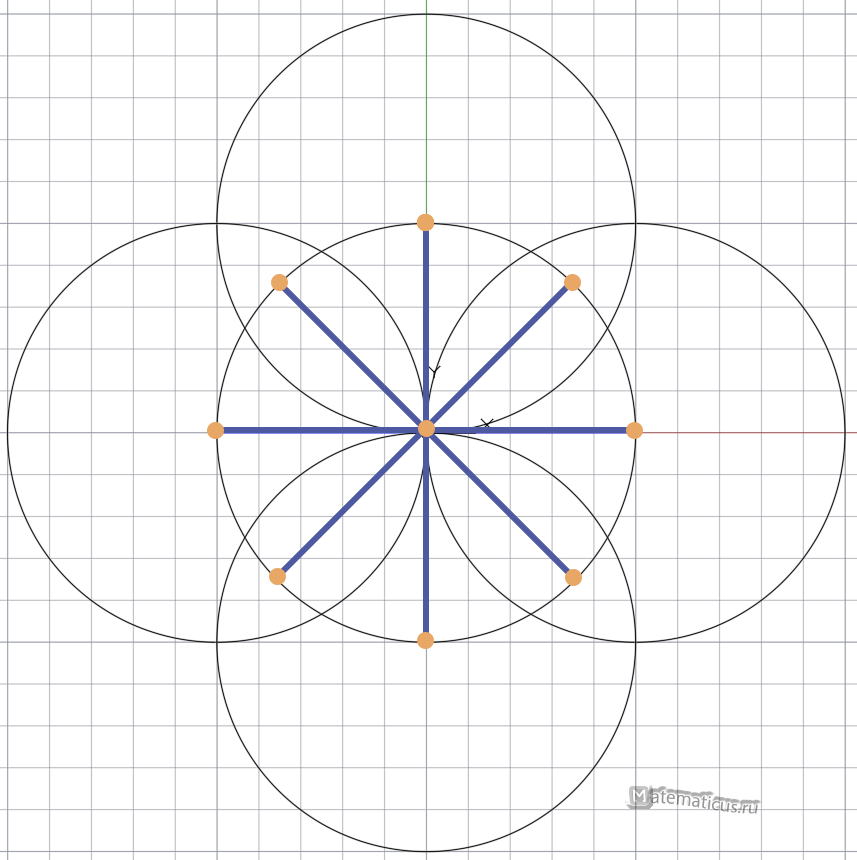
Соединяем точки с центром основной окружности и тем самым делим окружность на 8 равных частей.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.1 / 5. Количество оценок: 14
- Как разделить круг на 8 частей
- Разделить круг на 8 частей поэтапно
- Деление круга на равные части
- Деление круга на равные по площади части радиусами
- Деление круга на равные по площади части параллельными хордами
- Деление круга на равные части радиусами
- Деление круга на равные части параллельными хордами
- 🎦 Видео
Видео:Деление окружности на 8 частейСкачать

Как разделить круг на 8 частей

Раз вы на этом сайте, то скорее всего любите рисовать. Но при чем же здесь уроки геометрии? (спросите). Дело в том, что некоторые моменты построения пространства или каких-то предметов без точных «вычислений» не получится сделать.
Я слово «вычислений» взял в кавычки так как, это сильно сказано. Я сам не очень люблю копаться в формулах, но мы этого делать и не будем.
Я подбираю методы наименее травматичные для нашего мозга 🙂 , которые идеально подходят для художников, и совсем не собираюсь тесно связывать свой сайт с геометрией.
Давайте представим, что нам нужно нарисовать бриллиант, у которого восемь граней. Мы задумали картину на тему «Лучшие друзья девушек», и нужно сделать восьмигранный алмаз.
И здесь как раз нам поможет методика разделения круга на восемь равных частей. Будем делить вначале на четыре части, это так же пригодится для будущих шедевров 🙂 .
Видео:Деление окружности на равные части с помощью циркуляСкачать

Разделить круг на 8 частей поэтапно
Круг поделим без перспективы (фронтально), как его потом положить на плоскость это мы увидим в другом уроке.
Хочу заметить, что:
- Разметить на три и шесть частей,
- Разделить на 5 частей,
- Так же на семь частей
- Десять одинаковых частей
эти уроки у нас есть, смотрите их по ссылкам, а сейчас посмотрим, как разделить круг на 8 частей, ну и на 4.
Рисуем круг (окружность). Определим диаметр (горизонталь) АВ.
Что бы найти перпендикулярную прямую (вертикаль) отмечаем циркулем расстояние немного больше нашего радиуса и рисуем дугу (центр точка В), рисунок внизу.
Дальше такая же процедура, только центр будет в точке А.
Из пересечения эти двух кривых (серый пунктир) проводим отрезок CD (это будет вертикальный диаметр окружности). В центре поставим точку О. Смотрите на нижнюю иллюстрацию.
Ну, что же теперь разделим окружность на 4 части (зеленый квадрат)
Дальше возьмем радиус ВО (с центром В) и нанесем первую дугу.
После берем тот же радиус и изобразим дугу номер два (с центром С).
И через перекрестие дуг и точку О создадим прямую.

Тоже самое сделаем на правой стороне рисунка. Рисуем овал с центром в точке С. Второй овал с центром в точке А.
Дальше из пересечения кривых и точки О проложим прямую.
Теперь есть все нужное что бы поделить круг на 8 частей.
Окончательный результат ниже на картинке.

Не так это и сложно, но иногда без подсказки трудно найти решение.
Видео:Как разделить окружность на 8 частей How to divide a circle into 8 partsСкачать

Деление круга на равные части
Статья содержит два калькулятора, рассчитывающие параметры деления круга на равные по площади части радиусами и параллельными хордами
Ниже представлены два калькулятора, рассчитывающие параметры разделения круга на равные части. Сначала — традиционный калькулятор, который делит круг на равные части радиусами (примерно так, как режут пиццу или торт), под ним — нетрадиционный калькулятор, который делит круг на равные по площади части параллельными хордами. Оба калькулятора визуализируют результат рисунком. Методы расчета с формулами для обоих калькуляторов приведены ниже, под калькуляторами.
Деление круга на равные по площади части радиусами
Деление круга на равные по площади части параллельными хордами
Деление круга на равные части радиусами
Традиционный и очень простой метод деления круга — по факту, нарезка равных секторов. Метод и формулы очень просты:
- Определяем угловой размер каждого сектора в радианах, путем деления 360 градусов на нужное число секторов.
- Определяем размер дуги сектора, перемножая радиус на угол в радианах
- Определяем размер хорды по теореме косинусов (хорда является основанием равнобедренного треугольника с боковыми сторонами R и противолежащим углом альфа.
Собственно и всё — мы получили все характеристики для N равных секторов
Деление круга на равные части параллельными хордами
Этот способ более любопытен, чем предыдущий. Для простоты будем рассматривать верхнюю половину круга, так как с нижней все будет симметрично.
Задача состоит в определении x-вой координаты точек, через которые нужно проводить хорды (на рисунке это точки x1 и x2). Выведем для начала формулу площади куска, отсекаемого хордой слева.
Верхнюю полуокружность можно представить графиком функции y=f(x), где x — это координата вдоль оси абсцисс, а y — это функция, численно равная y координате соответствующей точки верхней полуокружности.
По теореме Пифагора получаем следующую функцию
Чтобы получить площадь фигуры, отсекаемой хордой слева, надо проинтегрировать эту функцию от -R до x. Первообразная функции равна:
Осталось определиться с константой. Нам надо, чтобы в точке с координатами -R площадь была равна нулю. Подставив -R вместо x в формулу выше, получаем
Итак, полное выражение
Теперь рассмотрим нахождение координат крайней левой точки. Нам известна площадь, которую она должна отсечь (напоминаю, речь идет о полуокружности)
Таким образом мы можем приравнять
Что дает нам такое финальное уравнение
Данное уравнение является трансцендентным, а поэтому находить координату первой точки придется численным методом, например, методом бисекции или методом Ньютона. Калькулятор использует метод Ньютона.
Вторая и последующие точки находится аналогично, путем изменения размера отсекаемой площади. Для второй точки это будет , для третьей и так далее.
Зная координаты точек, несложно рассчитать все остальные параметры, в частности, длину хорды.
🎦 Видео
Задача как разрезать торт на 8 частей за 3 разреза?Скачать

Деление окружности на 3; 6; 12 равных частейСкачать

Построение 8 угольника циркулемСкачать

Деление окружности на 3 частиСкачать

Как разделить окружность на 8 равных частей?Или создать 8 угольник?Скачать

1 2 3 деление окружности на 7 равных частейСкачать

Деление окружности на 3, 4, 5, 6 и 7 равных частейСкачать

Как разделить окружность на 3 равные части How to divide a circle into 3 equal partsСкачать

Деление окружностиСкачать

Как разделить круг на равные частиСкачать

Деление окружностей на равные частиСкачать
КАК РАЗДЕЛИТЬ ОКРУЖНОСТЬ НА 12 РАВНЫХ ЧАСТЕЙ?Скачать

Деление окружности на 12 равных частейСкачать

деление окружности на произвольное число частейСкачать
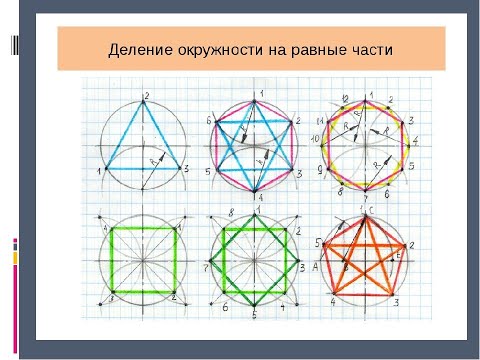
Деление окружности на равные части. Урок 6. (Часть 1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ)Скачать

Как поделить окружность на 3 равные части. Очень просто. Уроки черчения.Скачать

Деление окружности на 4 и 8 равных частейСкачать