Теоретическая механика:
Вращательное движение твердого тела

Смотрите также решения задач по теме «Вращательное движение» в онлайн решебниках Яблонского, Мещерского, Чертова (с примерами и методичкой для заочников), Иродова и Савельева.

При поступательном движении тела (§ 60 в учебнике Е. М. Никитина) все его точки движутся по одинаковым траекториям и в каждый данный момент они имеют равные скорости и равные ускорения.

Поэтому поступательное движение тела задают движением какой-либо одной точки, обычно движением центра тяжести.

Рассматривая в какой-либо задаче движение автомобиля (задача 147) или тепловоза (задача 141), фактически рассматриваем движение их центров тяжести.

Вращательное движение тела (Е. М. Никитин, § 61) нельзя отождествить с движением какой-либо одной его точки. Ось любого вращающегося тела (маховика дизеля, ротора электродвигателя, шпинделя станка, лопастей вентилятора и т. п.) в процессе движения занимает в пространстве относительно окружающих неподвижных тел одно и то же место.

Движение материальной точки или поступательное движение тела характеризуют в зависимости от времени линейные величины s (путь, расстояние), v (скорость) и а (ускорение) с его составляющими a_t и a_n.

Вращательное движение тела в зависимости от времени t характеризуют угловые величины : φ (угол поворота в радианах), ω (угловая скорость в рад/сек) и ε (угловое ускорение в рад/сек 2 ).

Закон вращательного движения тела выражается уравнением
φ = f (t).

Угловая скорость – величина, характеризующая быстроту вращения тела, определяется в общем случае как производная угла поворота по времени
ω = dφ/dt = f’ (t).

Угловое ускорение – величина, характеризующая быстроту изменения угловой скорости, определяется как производная угловой скорости
ε = dω/dt = f» (t).

Приступая к решению задач на вращательное движение тела, необходимо иметь в виду, что в технических расчетах и задачах, как правило, угловое перемещение выражается не в радианах φ, а в оборотах φ_об.

Поэтому необходимо уметь переходить от числа оборотов к радианному измерению углового перемещения и наоборот.

Так как один полный оборот соответствует 2π рад, то
φ = 2πφ_об и φ_об = φ/(2π).

Угловая скорость в технических расчетах очень часто измеряется в оборотах, произведенных в одну минуту (об/мин), поэтому необходимо отчетливо уяснить, что ω рад/сек и n об/мин выражают одно и то же понятие – скорость вращения тела (угловую скорость), но в различных единицах – в рад/сек или в об/мин.

Переход от одних единиц угловой скорости к другим производится по формулам
ω = πn/30 и n = 30ω/π.

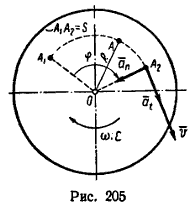
При вращательном движении тела все его точки движутся по окружностям, центры которых расположены на одной неподвижной прямой (ось вращающегося тела). Очень важно при решении задач, приведенных в этой главе, ясно представлять зависимость между угловыми величинами φ, ω и ε, характеризующими вращательное движение тела, и линейными величинами s, v, a_t и a_n, характеризующими движение различных точек этого тела (рис 205).

Если R – расстояние от геометрической оси вращающегося тела до какой-либо точки А (на рис. 205 R=OA), то зависимость между φ – углом поворота тела и s – расстоянием, пройденным точкой тела за то же время, выражается так:
s = φR.

Зависимость между угловой скоростью тела и скоростью точки в каждый данный момент выражается равенством
v = ωR.

Касательное ускорение точки зависит от углового ускорения и определяется формулой
a_t = εR.

Нормальное ускорение точки зависит от угловой скорости тела и определяется зависимостью
a_n = ω 2 R.

При решении задачи, приведенной в этой главе, необходимо ясно понимать, что вращением называется движение твердого тела, а не точки. Отдельно взятая материальная точка не вращается, а движется по окружности – совершает криволинейное движение.

Видео:Вращательное движение. 10 класс.Скачать

§ 33. Равномерное вращательное движение

Если угловая скорость ω=const, то вращательное движение называется равномерным.

Уравнение равномерного вращения имеет вид
φ = φ₀ + ωt.

В частном случае, когда начальный угол поворота φ₀=0,
φ = ωt.

Угловую скорость равномерно вращающегося тела
ω = φ/t
можно выразить и так:
ω = 2π/T,
где T – период вращения тела; φ=2π – угол поворота за один период.

Видео:Урок 43. Криволинейное движение. Равномерное движение по окружности. Центростремительное ускорениеСкачать

§ 34. Равнопеременное вращательное движение

Вращательное движение с переменной угловой скоростью называется неравномерным (см. ниже § 35). Если же угловое ускорение ε=const, то вращательное движение называется равнопеременным . Таким образом, равнопеременное вращение тела – частный случай неравномерного вращательного движения.

Уравнение равнопеременного вращения
(1) φ = φ₀ + ω₀t + εt 2 /2
и уравнение, выражающее угловую скорость тела в любой момент времени,
(2) ω = ω₀ + εt
представляют совокупность основных формул вращательного равнопеременного движения тела.

В эти формулы входят всего шесть величин: три постоянных для данной задачи φ₀, ω₀ и ε и три переменных φ, ω и t. Следовательно, в условии каждой задачи на равнопеременное вращение должно содержаться не менее четырех заданных величин.

Для удобства решения некоторых задач из уравнений (1) и (2) можно получить еще две вспомогательные формулы.

Исключим из (1) и (2) угловое ускорение ε:
(3) φ = φ₀ + (ω + ω₀)t/2.

Исключим из (1) и (2) время t:
(4) φ = φ₀ + (ω 2 — ω₀ 2 )/(2ε).

В частном случае равноускоренного вращения, начавшегося из состояния покоя, φ₀=0 и ω₀=0. Поэтому приведенные выше основные и вспомогательные формулы принимают такой вид:
(5) φ = εt 2 /2;
(6) ω = εt;
(7) φ = ωt/2;
(8) φ = ω 2 /(2ε).

Видео:Физика - движение по окружностиСкачать

§ 35. Неравномерное вращательное движение

Рассмотрим пример решения задачи, в которой задано неравномерное вращательное движение тела.

Видео:Физика | Равномерное движение по окружностиСкачать

I. Механика

Видео:Криволинейное, равномерное движение материальной точки по окружности. 9 класс.Скачать

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Видео:Урок 44. Вращение твердого тела. Линейная и угловая скорость. Период и частота вращения.Скачать

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Видео:УСКОРЕНИЕ - Что такое равноускоренное движение? Как найти ускорение // Урок Физики 9 классСкачать

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Видео:Физика 9 класс (Урок№4 - Движение тела по окружности. Период и частота)Скачать

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Видео:РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ физика 9 ПерышкинСкачать

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Видео:Движение по окружности. Нормальное и тангенциальное ускорение | 50 уроков физики (4/50)Скачать

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Видео:Лекция 6.1 | Описание движения по окружности | Александр Чирцов | ЛекториумСкачать

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Видео:Урок 47. Неравномерное движение по окружности. Тангенциальное ускорениеСкачать

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Видео:Физика 10 класс (Урок№4 - Равномерное движение точки по окружности.)Скачать

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Видео:Формулы механики 2, движение по окружности, центростремительное ускорениеСкачать

Виды движения по окружности

Угловое движение можно условно разделить на два вида:

1. Когда изменяется только направление вектора линейной скорости, а его длина не изменяется.
2. Или, когда изменяются обе характеристики вектора линейной скорости.

Во втором случае, для описания движения будем применять более сложные формулы кинематики. Так как появится еще один вид ускорения.

Центростремительное (нормальное) ускорение есть всегда, когда есть движение по окружности, при этом не важно, меняется ли скорость тела по модулю, или не меняется.

Видео:Центростремительное ускорение. 9 класс.Скачать

Движение по окружности с постоянной по модулю скоростью

Пусть тело движется по окружности, но при этом длина вектора линейной скорости не меняется (рис. 1).

[left|vec right| = const]

На рисунке 1 указаны: а) – вид сбоку, б) вид сверху, вектор угловой скорости направлен к нам перпендикулярно рисунку.

Скорость будет меняться только по направлению от точки к точке, потому, что на тело действует центростремительная сила (displaystyle vec<F_<text>>) , тело обладает центростремительным (displaystyle vec<a_<text>>) (нормальным) ускорением.

Кроме линейной, тело обладает угловой скоростью. Если линейная скорость не изменяется по модулю, то длина вектора угловой скорости не меняется.

На рисунке 1а изображен вектор угловой скорости (displaystyle vec), на рисунке 1б вектор угловой скорости направлен к нам перпендикулярно плоскости рисунка. Направление, в котором тело движется по окружности, указано синей стрелкой.

Видео:Движение тел по окружностиСкачать

Тангенциальное ускорение – когда модуль скорости меняется

Тело может увеличивать или уменьшать свою скорость, когда движется по окружности.

В таком случае, дополнительно к нормальному ускорению возникает тангенциальное (displaystyle vec<a_>) ускорение.

Тангенциальное ускорение играет роль линейного ускорения при прямолинейном движении тела. Вектор (displaystyle vec<a_>) направлен параллельно вектору (displaystyle vec) скорости.

Подобно движению по прямой, вектор ускорения – это первая производная скорости по времени, или вторая производная перемещения по времени.

Когда векторы скорости (vec) и ускорения (vec<a_>) сонаправлены (рис. 2), линейная и угловая скорости возрастают.

А когда ускорение (vec<a_>) направлено противоположно (рис. 3) вектору скорости (vec), угловая и линейная скорости уменьшаются.

С линейной скоростью (vec) связана угловая (vec) скорость.

Из рисунков 2, 3 следует: когда появляется тангенциальное ускорение, меняется и угловая скорость. Значит, тангенциальное ускорение (vec<a_>) появляется совместно с угловым (vec) ускорением и между ними есть связь.

Связь между тангенциальным и угловым ускорением выглядит аналогично связи между линейной и угловой скоростью.

В векторном виде

В скалярном виде

[ large boxed < a_= beta cdot R >]

(displaystyle vec left( frac<text><c^>right)) – угловое ускорение;

(displaystyle vec< a_> left( frac<text><c^>right)) – тангенциальное ускорение;

(R left( textright)) – радиус окружности.

Видео:КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ - Угловое Перемещение, Угловая Скорость, Центростремительное УскорениеСкачать

Равноускоренное движение по окружности

Угловая скорость увеличивается (рис. 2), когда угловое ускорение сонаправлено с вектором угловой скорости. Когда движение происходит с постоянным ускорением, его называют равноускоренным.

Для решения задач на равноускоренное движение по окружности, поступаем аналогично равноускоренному движению по прямой. Применяем систему из двух уравнений:

[ large boxed < beginomega = omega _ + beta cdot t \ displaystyle varphi = omega_ cdot t + beta cdot frac end > ]

Первое уравнение системы – это связь между начальной (omega_ ) и конечной (omega ) скоростью. Второе уравнение – это уравнение движения.

Видео:Равномерное движение точки по окружности | Физика 10 класс #7 | ИнфоурокСкачать

Равнозамедленное движение по окружности

Когда векторы (vec) и (vec) направлены в противоположные стороны, угловая скорость (vec) уменьшается (рис. 3).

Для решения задач кинематики, в которых угловая скорость уменьшается и, движение равнозамедленное, используем систему, состоящую из таких уравнений:

[ large boxed < beginomega = omega _ — beta cdot t \ displaystyle varphi = omega_ cdot t — beta cdot frac end > ]

Видео:Ускорение при равномерном движении по окружностиСкачать

Общее ускорение при движении по окружности

Пусть точка движется по окружности и линейная (vec) скорость ее изменяется по модулю. При этом, точка обладает двумя видами ускорения — нормальным и тангенциальным. Эти виды ускорения обозначают символом (vec).

Примечание: Любое ускорение, обозначаемое символом «a», измеряется в метрах, деленных на секунду в квадрате.

Направление вектора общего ускорения указано на рисунке 4а, а для равнозамедленного – на рисунке 4б.

Так как векторы (vec<a_>) и (vec<a_>) всегда перпендикулярны, длину вектора общего ускорения (vec) можно найти из теоремы Пифагора: