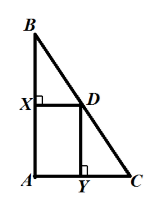Равноудаленная точка в треугольнике

Вы будете перенаправлены на Автор24

В треугольнике есть так называемые четыре замечательные точки: точка пересечения медиан. Точка пересечения биссектрис, точка пересечения высот и точка пересечения серединных перпендикуляров. Рассмотрим каждую из них.

Видео:Точка, равноудаленная от всех вершин многоугольникаСкачать

Точка пересечения медиан треугольника

О пересечении медиан треуголника: Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении $2:1$ начиная с вершины.

Доказательство.

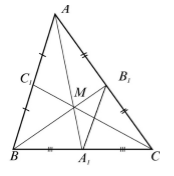
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его медианы. Так как медианы делят стороны пополам. Рассмотрим среднюю линию $A_1B_1$ (Рис. 1).

Рисунок 1. Медианы треугольника

По теореме 1, $AB||A_1B_1$ и $AB=2A_1B_1$, следовательно, $angle ABB_1=angle BB_1A_1, angle BAA_1=angle AA_1B_1$. Значит треугольники $ABM$ и $A_1B_1M$ подобны по первому признаку подобия треугольников. Тогда

Аналогично доказывается, что

Видео:Точка, равноудаленная от всех сторон многоугольникаСкачать

Точка пересечения биссектрис треугольника

О пересечении биссектрис треугольника: Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

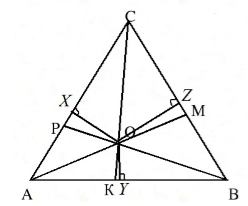
Рассмотрим треугольник $ABC$, где $AM, BP, CK$ его биссектрисы. Пусть точка $O$ — точка пересечения биссектрис $AM и BP$. Проведем из этой точки перпендикуляры к сторонам треугольника (рис. 2).

Рисунок 2. Биссектрисы треугольника

Готовые работы на аналогичную тему

Для доказательства нам потребуется следующая теорема.

Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.

По теореме 3, имеем: $OX=OZ, OX=OY$. Следовательно, $OY=OZ$. Значит точка $O$ равноудалена от сторон угла $ACB$ и, значит, лежит на его биссектрисе $CK$.

Видео:№199. Точка S равноудалена от вершин прямоугольного треугольника и не лежит в плоскости этогоСкачать

Точка пересечения серединных перпендикуляров треугольника

Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

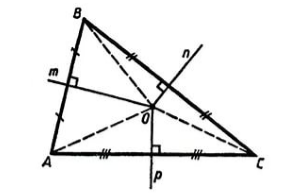
Пусть дан треугольник $ABC$, $n, m, p$ его серединные перпендикуляры. Пусть точка $O$ — точка пересечения серединных перпендикуляров $n и m$ (рис. 3).

Рисунок 3. Серединные перпендикуляры треугольника

Для доказательства нам потребуется следующая теорема.

Каждая точка серединного перпендикуляра к отрезку равноудалена от концов данного отрезка.

По теореме 3, имеем: $OB=OC, OB=OA$. Следовательно, $OA=OC$. Значит точка $O$ равноудалена от концов отрезка $AC$ и, значит, лежит на его серединном перпендикуляре $p$.

Видео:Геометрия Данная точка расположенная вне плоскости правильного треугольника равноудалена от егоСкачать

Точка пересечения высот треугольника

Высоты треугольника или их продолжения пересекаются в одной точке.

Доказательство.

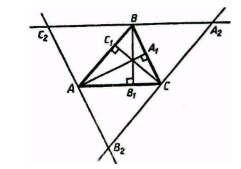
Рассмотрим треугольник $ABC$, где $_1, _1, _1$ его высоты. Проведем через каждую вершину треугольника прямую, параллельную противоположной вершине стороне. Получаем новый треугольник $A_2B_2C_2$ (рис. 4).

Рисунок 4. Высоты треугольника

Так как $AC_2BC$ и $B_2ABC$ параллелограммы с общей стороной, то $AC_2=AB_2$, то есть точка $A$ — середина стороны $C_2B_2$. Аналогично, получаем, что точка $B$ — середина стороны $C_2A_2$, а точка $C$ — середина стороны $A_2B_2$. Из построения мы имеем, что $_1bot A_2B_2, _1bot A_2C_2, _1bot C_2B_2$. Следовательно, $_1, _1, _1$ — серединные перпендикуляры треугольника $A_2B_2C_2$. Тогда, по теореме 4, имеем, что высоты $_1, _1, _1$ пересекаются в одной точке.

Видео:Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Пример задачи на использование 4 замечательных точек треугольника

Серединные перпендикуляры к сторонам $AB$ и $AC$ треугольника $ABC$ пересекаются в точке $D$ стороны $BC$. Докажите, что

а) точка $D$ — середина стороны $BC$.

б) $angle A=angle B+angle C$

Решение.

а) По теореме 4, все серединные перпендикуляры пересекаются в точке $D$. Следовательно, $D$ — основание серединного перпендикуляра к стороне $BC$. Значит точка $D$ — середина стороны $BC$.

б) Так как $X$ и $D$ — середины сторон, то $XD$ — средняя линия треугольника. Тогда, по теореме о средней линии треугольника $XD||AC$. Значит,$angle A=angle DXB$, как соответственные углы. Значит, $angle A=^0$. Тогда$angle B+angle C=^0-angle A=^0-^0=^0=angle A$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2022

Видео:Урок по теме ЧЕТЫРЕ ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА ГЕОМЕТРИЯ 8 КЛАСССкачать

Ззамечательные точки треугольника — свойства, применение и примеры решения

Замечательные точки треугольника не просто так описываются таким прилагательным. Для многих учеников, а начинают знакомиться с этим понятием в 8 классе, эта тема кажется наиболее интересной и простой в курсе геометрии, поэтому многочисленные теоремы и свойства запоминаются достаточно просто.

Итак, какие же четыре точки называются замечательными? Перечислим их:

точку пересечения медиан треугольника;

точку пересечения биссектрис треугольника;

точку пересечения высот треугольника;

точку пересечения серединных перпендикуляров сторон треугольника.

Все точки обладают своими особенностями и свойствами, про всех есть свои теоремы и следствия из них. Кроме того, существует свойство, которое справедливо сразу для четырёх этих точек. Вне зависимости от того, медиана ли это, биссектриса или высота, все они пересекаются в одной точке.

Замечательные точки характерны не только для треугольников. Например, в трапеции так же четыре замечательные точки.

Теперь рассмотрим основные положения, связанные с замечательными точками треугольника.

Видео:Замечательные точки треуг-ка. 8 класс.Скачать

Точка пересечения медиан треугольника

Из курса геометрии известно определение медианы треугольника.

На данном рисунке она обозначена прямой m, которая исходит из вершины А и заканчивается точкой М, являющейся центром стороны ВС.

Теперь сделаем чертёж треугольника, на котором укажем замечательную точку пересечения медиан.

Для начала постройте абсолютно любой треугольник и обозначьте его буквами А, В и С.

На отрезке АВ отметьте центр С1, на стороне ВС центр А1, на АС центр В1.

Проведите 3 медианы из вершин. Из угла А – медиана АА1,из угла В — медиана ВВ1, из угла С — медиана СС1.

Должно получиться так, как показано на рисунке: три проведённые линии пересекаются в одной точке G (что является их свойством).

Изучим следующее свойство точки пересечения трёх медиан треугольника.

Отрезки медианы треугольника, разделённой замечательной точкой, относятся друг к другу как 2:1. Проследим это свойство на примере используемого нами рисунка:

A1G = 2AG, B1G = 2BG, C1G = 2CG.

Видео:№143. Расстояние от точки М до каждой из вершин правильного треугольника ABC равно 4 смСкачать

Точка пересечения биссектрис треугольника

Прежде чем мы приступим к изучению следующей точки, рассмотрим теорему о биссектрисе, проведённой из вершины неразвёрнутого угла, и докажем её.

Рассмотрим пример. Дано:

угол ВАС Точка пересечения серединных перпендикуляров сторон треугольника

Для начала вспомним определение серединного перпендикуляра. Теорема о серединном перпендикуляре:

Сделаем краткое доказательство. Соединим концы отрезка с вершиной серединного отрезка. Докажем равенство полученных треугольников, из чего следует АD = DB.

Построим эту точку.

В треугольнике АВС отмечаем середины его сторон. Проводим три серединных перпендикуляра КО, LO, МО и отмечаем точку их пересечения О.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Точка пересечения высот треугольника

Проведём три высоты в ∆АВС, все они пересекутся в т. Н. Точка Н по отношению к ∆АВС – ортоцентр.

Свойство высот треугольника:

если все три высоты треугольника или их продолжения пересекаются в одной точке, то это ортоцентр;

СH * HНС
= АH * АНА = ВH * ВНВ.

Ортоцентр может располагаться внутри треугольника, снаружи или совпадать с одной из вершин.

На рисунке показано расположение ортоцентра в остроугольном, прямоугольном и тупоугольном треугольниках.

Видео:№948. На оси ординат найдите точку, равноудаленную от точек: а) А (-3; 5)Скачать

Пример решения задач с построением

Замечательные точки треугольника замечательные именно потому, что они имеют много полезных для решения задач свойств. Рассмотрим пример решения задачи на эту тему.

Серединный перпендикуляр в ∆АВС, опущенный к АС, пересекает ВС в т. В. Найти BD, DC, если AD = 5 см BC = 9 см.

Сделаем дополнительное построение – серединный отрезок КD к прямой АС. Тогда DK это и высота, и медиана в ∆АВС. Если в треугольнике проведена прямая, которая является высотой и медианой, то он равнобедренный. Значит, AD = DC = 5 см.

ВD =ВС — DC = 4 см.

Ответ: DC = 5 см, ВD = 4 см.

Видео:Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

Четыре замечательные точки треугольника — справочник студента

§ 1 Теорема о биссектрисе угла

• С любым треугольником в геометрии связаны четыре точки:
• 1) точка пересечения медиан;
• 2) точка пересечения биссектрис;
• 3) точка пересечения высот (или их продолжений);
• 4) точка пересечения серединных перпендикуляров к сторонам.

1. Эти четыре точки называют замечательными точками треугольника.
2. В этом уроке рассмотрим и докажем теоремы, следствия из этих теорем, связанные с замечательными точками треугольника, и рассмотрим их применение при решении задач.
3. Познакомимся сначала с теоремой о биссектрисе угла.
4. Теорема:
5. Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон.
6. Обратно:
7. Каждая точка, лежащая внутри угла и равноудаленная от сторон угла, лежит на его биссектрисе.
8. Докажем эти утверждения.
9. Дано:
10. ∠ВАС, АМ – биссектриса, МК и МL перпендикулярны к прямым АВ и АС.
11. Доказать:
12. МК = МL
13. Доказательство:

• Рассмотрим прямоугольные треугольники АКМ и АLМ.
• Они равны по гипотенузе и острому углу (АМ – общая сторона, ∠1 = ∠2 , так как по условию АМ – биссектриса).
• Из равенства треугольников следует МК = МL.
• Теперь докажем обратное утверждение.
• Дано:
• ∠ВАС, точка М лежит внутри угла и равноудалена от сторон угла АВ и АС.
• Доказать:
• луч АМ – биссектриса ∠ВАС.
• Доказательство:

1. Проведем перпендикуляры МК и МL к прямым АВ и АС.
2. Прямоугольные треугольники АМК и АМL равны по гипотенузе и катету (АМ – общая гипотенуза, МК = МL по условию).
3. Следовательно, ∠1 = ∠2, это означает, что луч АМ – биссектриса ∠ВАС.
4. Теорема доказана.
5. Из утверждения теоремы следует еще одно утверждение.
6. Следствие: биссектрисы треугольника пересекаются в одной точке.

§ 2 Теорема о серединном перпендикуляре к отрезку

• Перейдем к теореме о серединном перпендикуляре к отрезку.
• Но сначала дадим определение.
• Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

1. На рисунке прямая а является серединным перпендикуляром к отрезку АВ.
2. Теорема:
3. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.
4. Обратно:
5. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
6. Дано:
7. АВ – отрезок, прямая m – серединный перпендикуляр к отрезку АВ, точка О – середина этого отрезка.
8. М – произвольная точка прямой m.
9. Доказать: АМ = ВМ
10. Доказательство:
11. Если точка М совпадает с точкой О, то равенство АМ = ВМ верно.

• Пусть М и О – различные точки.
• Прямоугольные треугольники ОАМ и ОВМ равны по двум катетам (ОА = ОВ по условию, ОМ – общий катет), из равенства треугольников следует, что АМ = ВМ.
• Докажем обратное утверждение.
• Дано:
• АВ – отрезок, N – произвольная точка такая, что АN = ВN.
• Доказать:
• точка N лежит на прямой m – серединном перпендикуляре к АВ.
• Доказательство:
• если точка N – точка прямой АВ, то она совпадает с серединой О отрезка АВ и потому лежит на прямой m.

Если же точка N не лежит на прямой АВ, то треугольник АNВ – равнобедренный, так как АN = ВN.

Отрезок NО является медианой равнобедренного треугольника, значит, она является и его высотой.

Таким образом, NО перпендикулярен АВ, поэтому прямые ОN и m совпадают, т.е. точка N – точка прямой m.

1. Теорема доказана.
2. Следствием доказанной теоремы является следующее утверждение.
3. Следствие: серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

§ 3 Теорема о пересечении высот теугольника

• Рассмотрим еще одну теорему о пересечении высот треугольника.
• Теорема:
• Высоты треугольника (или их продолжения) пересекаются в одной точке.
• Дано:
• АА1 , ВВ1, СС1 – высоты треугольника АВС.
• Доказать:
• АА1 , ВВ1, СС1 пересекаются в точке О.
• Доказательство:

1. Проведем через вершины А, В и С прямые, параллельные противоположным сторонам треугольника.
2. Получим треугольник А2В2С2.
3. Точки А, В, С являются серединами треугольника А2В2С2.

Действительно, в параллелограммах АВА2Си АВСВ2 противоположные стороны равны, т.е. АВ = А2С, АВ = СВ2 , поэтому А2С = СВ2.

• Аналогично С2А = АВ2 и С2В = ВА2.
• Из построения следует, что СС2 перпендикулярно А2В2, АА1 перпендикулярно В2С2, ВВ1 перпендикулярно А2С2.
• Таким образом, прямые АА1, ВВ1, СС1 являются серединными перпендикулярами к сторонам треугольника А2В2С2, следовательно, они пересекаются в одной точке.
• Теорема доказана.
• Решим задачу, используя полученные знания.
• Задача.
• В треугольнике АВС проведены высоты АК и ВD, пересекающиеся в точке О.
• Угол САВ = 42°.
• Найдите величину угла АСО.
• Дано:
• ∆АВС, АК и ВD – высоты треугольника АВС, пересекающиеся в точке О, ∠САВ = 42°
• Найти:
• ∠АСО.
• Решение:

1. для вычисления угла АСО проведем еще одну высоту СМ треугольника АВС, по теореме о пересечении высот треугольника высота СМ пройдет через точку О, а значит, треугольник АСМ – прямоугольный.
2. Тогда ∠АСО = 180° – (90° + 42°) = 48°.
3. В этом уроке познакомились с замечательными точками треугольника, рассмотрели теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку и их следствия, теорему о пересечении высот (или их продолжений), а также рассмотрели решение задачи по теме урока.

Список использованной литературы:

1. Л.С. Атанасян. Учебник. 8 класс.
2. Н.Ф. Гаврилова. Поурочные разработки по геометрии. 8 класс. – Москва: «Вако», 2005.
3. Л.С. Атанасян и др. Методические рекомендации к учебнику. – Москва: «Просвещение», 2001.
4. Д.А. Мальцева. Математика. 9 класс. ГИА 2014. – Москва: Народное образование, 2013.
5. О.В. Белицкая. Геометрия. 8 класс. Тесты. – Саратов: «Лицей», 2009.
6. С.П. Бабенко, И.С. Маркова. Геометрия 8. Комплексная тетрадь для контроля знаний. – Москва: «Аркти», 2014.

Видео:четыре замечательные точки треугольника 8 КЛАСС АтанасянСкачать

Замечательные точки треугольника — урок. Геометрия, 8 класс

Теорема 1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.

Теорема 2. (обратная) Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.

Теорема 3. Каждая точка серединного перпендикуляра к отрезку равноудалена от его концов.

Теорема 4. (обратная) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.

Первая замечательная точка треугольника — точка пересечения биссектрис

Теорема 5. Биссектрисы треугольника пересекаются в одной точке.

(AN), (BM) — биссектрисы, (O) — точка их пересечения.

Является ли биссектрисой (CK)? Если точка (O) равноудалена от сторон (AB) и (AC) и от сторон (BA) и (BC), то она лежит на биссектрисе угла ∡C, так как равноудалена от сторон угла.

Эта точка и есть центр вписанной в треугольник окружности, всегда находится в треугольнике.

Вторая замечательная точка треугольника — точка пересечения серединных перпендикуляров сторон треугольникаТеорема 6. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Допустим, точка (O) — точка пересечения двух серединных перпендикуляров сторон (AB) и (BC). Она равноудалена и от точек (A) и (B), и от точек (B) и (C). Следовательно, она лежит на серединном перпендикуляре стороны (AC), так как равноудалена от её конечных точек.

Эта точка и есть центр описанной около треугольника окружности, находится в треугольниках с острыми углами, вне треугольника с тупым углом и на гипотенузе прямоугольного треугольника.

Третья замечательная точка треугольника — точка пересечения медиан

Теорема 7. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении (2 : 1), считая от вершины.

Точка пересечения медиан является центром тяжести треугольника.

Четвёртая замечательная точка треугольника — точка пересечения высот треугольника

Теорема 8. Высоты треугольника или их продолжения пересекаются в одной точке.

Точка пересечения высот называется ортоцентром треугольника.

В (1765) году немецкий математик Эйлер доказал, что в любом треугольнике ортоцентр, центр тяжести и центр описанной окружности лежат на одной прямой, названой позже прямой Эйлера.

В двадцатых годах (XIX) века французские математики Понселе, Брианшон и другие установили независимо друг от друга следующую теорему: основания медиан, основания высот и середины отрезков высот, соединяющих ортоцентр с вершинами треугольника, лежат на одной и той же окружности.

Видео:8 класс, 35 урок, Свойства биссектрисы углаСкачать

Четыре замечательные точки треугольника — урок 3

Цели: рассмотреть теорему о точке пересечения высот треугольника.

I. Проверка домашнего задания.

1. Найти: РВKС, РАВС.

2. FK, FN серединные перпендикуляры.

• АВ = 16
• СF = 10
• Найти расстояние от точки F до стороны АВ.

II. Изучение нового материала.

Теорему о точке пересечения высот треугольника учителю желательно прокомментировать по заранее заготовленному чертежу, а детальное доказательство предложить учащимся провести дома самостоятельно или с помощью учебника.

III. Закрепление изученного материала.

Дуга АD – полуокружность.

2. Решить №№ 677, 684, 687.

1) АВО = 180° – АВN = 180° – СВN = CВО, то есть ВО – биссектриса АВС, аналогично СО – биссектриса АСВ.

2) По теореме о биссектрисе угла точка О равноудалена от сторон АВ, ВС, АС. Таким образом, ОН1 = ОН2 = ОН3, где ОН1 АВ, ОН2 ВС, ОН3 АС.

2. Получили, что АВ, ВС, АС – касательные к окружности с центром в точке О и радиусом, равным ОН1.

1) По свойству углов при основании равнобедренного треугольника САВ = СВА.

2) МАВ – равнобедренный, АМ = ВМ и точка М лежит на серединном перпендикуляре к АВ.

3) Так как АС = СВ, то точка С также лежит на серединном перпендикуляре к АВ. Таким образом, СМ АВ.

1. № 687.
2. Решение
3. 1) Построим серединный перпендикуляр m к отрезку АВ.
4. 2) Точка М – точка пересечения m c а.
5. 3) М – искомая.
6. Задача имеет решение в случае, если прямая АВ не перпендикулярна к данной прямой а.

• Четыре замечательные точки треугольника.
• 1) О – точка пересечения медиан треугольника АВС.
• АМ : МА1 = ВМ = МВ1 = СМ = МС1 = 2 : 1.
• 2) K – точка пересечения серединных перпендикуляров к сторонам треугольника АВС.
• АK = KС = KВ.
• 3) М – точка пересечения биссектрис углов треугольника АВС.
• МС1 = МА1 = МВ1.
• 4) N – точка пересечения высот треугольника (или их продолжений).

Домашнее задание: вопросы 1– 20, с. 187–188; №№ 688, 720.

Рекомендовать решать № 720 методом от противного.

Полуокружность с концами АВ и отмечена точка K. С помощью одной линейки постройте прямую, проходящую через точку K и перпендикулярную к прямой АВ.

Использовать решение и чертеж устной задачи урока.

Видео:Три точки, задающие окружностьСкачать

Презентация на тему: Четыре замечательные точки треугольника

Описание слайда:

Четыре замечательные точки треугольника

Описание слайда:

Свойство биссектрисы неразвёрнутого угла Теорема1. Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон. Теорема 2 ( обратная).

Точка, лежащая внутри неразвёрнутого угла и равноудалённая от его сторон, лежит на биссектрисе этого угла.

Обобщённая теорема: биссектриса неразвёрнутого угла – множество точек плоскости, равноудалённых от сторон этого угла. Дано: ВАС, АХ – биссектриса, М є АХ, МЕ АВ, МК АС

Описание слайда:

Серединный перпендикуляр к отрезку Теорема 1. Каждая точка серединного перпендикуляра к отрезку равноудалена от его концов. Дано: АВ – отрезок, РК – серединный перпендикуляр,М є РК Теорема 2. Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему. Обобщённая теорема: серединный перпендикуляр к отрезку – множество точек плоскости, равноудалённых от его концов.

Описание слайда:

Первая замечательная точка треугольника Теорема. Биссектрисы треугольника пересекаются в одной точке.

Дано: АВС, АЕ, ВТ – биссектрисы, О — точка их пересечения Доказать: СУ – биссектриса АВС, О є СУ АЕ – биссектриса и ОМ АВ, ОК АС,значит, ОМ = ОК ВТ – биссектриса, и ОМ АВ, ОР ВС, значит, ОМ = ОP Значит, ОМ = ОК = ОР и ОР ВС, ОК АС, следовательно, О лежит на биссектрисе угла АСВ, т. е. СУ – биссектриса АВС. Значит, О – точка пересечения трёх биссектрис треугольника.

Описание слайда:

Вторая замечательная точка треугольника Теорема. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Дано: АВС, k,n – серединные перпендикуляры к сторонам треугольника, О – точка их пересечения Доказать: р – серединный перпендикуляр к ВС, О є р k – серединный перпендикуляр к АВ и О є k, значит, ОА = ОВ.

Следовательно, ОА = ОВ =ОС, значит, О лежит на серединном перпендикуляре к стороне ВС, т. е. на р.

Описание слайда:

Вторая замечательная точка треугольника (продолжение) Ещё возможное расположение:

Описание слайда:

Третья замечательная точка треугольника Теорема. Медианы треугольника пересекаются в одной точке, которая делит каждую в отношении 2: 1, считая от вершины. (центр тяжести треугольника – центроид) Дано: АВС, AM,ВК,СР — медианы Доказать: АМ ВК СР = О Доказательство проведено ранее: задача 1 п. 62.

Описание слайда:

Четвёртая замечательная точка треугольника Теорема. Высоты треугольника или их продолжения пересекаются в одной точке(ортоцентр). Доказать: О – точка пересечения высот или их продолжений.

Описание слайда:

Доказательство: Через вершины В, А, С треугольника АВС проведём ЕТ АС, ЕУ ВС, ТУ АВ. Получим: АСВЕ – параллелограмм, значит, АС = ВЕ АСТВ – параллелограмм, значит, АС = ВТ Следовательно, ВЕ = ВТ, т. е. В – середина ЕТ. Т.к.

ВН – высота АВС по условию, то ВН АС Получим: ВН – серединный перпендикуляр к ЕТ. Аналогично, СМ – серединный перпендикуляр к ТУи АК — серединный перпендикуляр к УЕ. Т. е.

ВН, СМ, АК – серединные перпендикуляры к сторонам ЕТУ, которые по ранее доказанному пересекаются в одной точке,значит, высоты АВС пересекаются в одной точке.

Описание слайда:

Дано: АВС, АМ = ВМ, МD AB, AK = KC, DK AC, D є BC. Доказать: D — середина ВС, А = В + С. D є BC по условию, значит, ВD = AD AK = KC, DK AC, D є BC по условию, значит, AD = DC следовательно, D – середина ВС. б) По доказанному AD = DC, значит, треугольники АВD и АСD – равнобедренные, поэтому 1 = В, 2 = С. ВАС = 1 + 2 = В + С, что и т. д.

Видео:№275. На основании АВ равнобедренного треугольника ABC взята точка М, равноудаленная от боковыхСкачать

Четыре замечательные точки треугольника

• Цели:
• Выяснить какие точки в треугольнике являются «Замечательными» и каково их назначение; Изучить и обобщить научные сведения по теме «Замечательные точки в треугольнике».
• Задачи: Рассмотреть основные теоремы, связанные с замечательными точками в треугольнике; Рассмотреть пересечение линий в треугольнике, пользуясь техникой оригами;
• Обобщить изученный материал при заполнении индивидуальных карточек.
• Ход урока

Чтобы узнать о какой фигуре мы сегодня будем вести речь посмотрите рисунки и скажите какая фигура встречается чаще всего?(Треугольник)Правильно треугольник .

Удивительно, но треугольник, несмотря на свою кажущуюся простоту, является неисчерпаемым объектом изучения — никто даже в наше время не осмелится сказать, что изучил и знает все свойства треугольника. Действительно, кто не слышал о Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? А ведь сам треугольник таит в себе немало интересного и загадочного.

Тема нашего сегодняшнего урока «Четыре замечательные точки треугольника» . Откройте тетради, запишите сегодняшнее число классная работа и тему урока. Скажите, а что означает слово «Замечательный» в нашей жизни?

А в математике с чем это связано? ( с какими то свойствами той или иной фигуры).

К знаниям мы будем идти различными путями, как вы думаете какими способами можно получить информацию по теме нашего урока?

Для того, чтобы начать изучение нового материала, нам придётся опереться на уже изученный материал, а так же мы будем учиться оформлять новый и пройденный материал схематически. Что за отрезок вы видите на рисунке?(Медиана)

Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Любой треугольник имеет три медианы.

Биссектрисой называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной. Любой треугольник имеет три биссектрисы.

1. (Высота)
2. Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение. Любой треугольник имеет три высоты
3. (Серединный перпендикуляр)
4. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярно к нему. Любой треугольник имеет три серединных перпендикуляра
5. Повторение определений основных линий в треугольнике (при помощи презентации), путём фронтальной беседы.

Мы вспомнили, что в треугольнике три медианы, три биссектрисы, три высоты, и три серединных перпендикуляра. Давайте с вами исследуем как эти отрезки пересекаются а треугольнике. Для этого мы проведем практическую работу.

• Практическая работа
• 1) Работа с чертёжными инструментами на доске (4 ученика): построение биссектрис, медиан, высот, серединных перпендикуляров в треугольнике.(остальные работают в группах)
• 2) Работа с бумагой (работа по рядам)Каждый ряд получает задание (используя треугольный лист бумаги): построить сгибанием точку пересечения медиан, биссектрис.(2 человека)
• Итак давайте посмотрим и сделаем вывод.
• Что произошло с биссектрисами, медианами, высотами, серединными перпендикулярами? (они пересекаются в одной точке)
• Ребята, именно эти точки называются « Замечательными точками треугольника»
• Объяснение нового материала

Обратите внимание на слайд. Рассмотрим точку пересечения биссектрис. Подумайте, как можно вписать окружность в треугольник? Какого элемента не достаёт, для построения окружности? Конечно же – центра окружности.

1. Точка пересечения биссектрис является центром вписанной окружности.

2. Точка пересечения серединных перпендикуляров к сторонам треугольника является центром описанной окружности.

3.Точка пересечения медиан, называется центром тяжести треугольника.

4. Точка пересечения высот называется ортоцентр.

1. А сейчас докажем с вами одну из теорем. – смотрите презентацию
2. IV.Закрепление (самостоятельная работа обучающего характера)
3. Откройте учебники и найдите №677

V. Итог урока.

Итак давайте мы с вами подведём итог того, что мы сегодня узнали на уроке. На ваших столах лежат схемы, ваша задача заполнить её. – смотрите документ.

• V.Рефлексия
• Скажите что мы сегодня делали на уроке, чтобы изучить тему?
• VI.Домашнее задание
• №677(678)
• Творческое задание: исследовать как пересекаются высоты в прямоугольном, тупоугольном и остроугольном треугольниках.
• Ребята наш урок подходит к концу и сейчас я прошу вас на обратной стороне таблицы написать как вы оцениваете свою деятельность на уроке.

Видео:№238. Докажите, что в равнобедренном треугольнике отрезок, соединяющий любую точку основания,Скачать

Четыре замечательные точки треугольника

Коканова Надежда Петровна

Цели:— обобщить знания учащихся потеме «Четыре замечательные точки треугольника», продолжить работу по формированию навыков построения высоты, медианы, биссектрисы треугольника;

— познакомить учащихся с новыми понятиями вписанной окружности в треугольник и описанной около него;

— развивать навыкиисследования;- воспитывать настойчивость, точность, организованностьучащихся.

Задача: расширить познавательный интерес к предметугеометрия.

Оборудование:доска, чертёжные инструменты, цветные карандаши, модель треугольника на альбомном листе; компьютер, мультимедийный проектор, экран.

Ход урока

1. Организационный момент (1 минута)Учитель: На этом уроке каждый из вас почувствует себя в роли инженера-исследователя, после окончания практической работы вы сможете оценить себя. Чтобы работа была успешна, надо очень точно и организовано выполнять все действия с моделью в ходе урока. Желаю успеха.2. Подготовка к основному этапу урока (10-13 минут).Учитель: начертите в тетради неразвёрнутый угол

В. Какие вы знаете способы построения биссектрисы угла?

Определение биссектрисы угла. Два ученика выполняют на доскепостроение биссектрисы угла (по заранее заготовленным моделям) двумя способами: линейкой, циркулем. Следующие два ученика устнодоказывают утверждения:1. Каким свойством обладают точки биссектрисы угла?2. Что можно сказать о точках, лежащих внутри угла иравноудалённых от сторон угла?

Учитель: начертите в тетрадиостроугольный треугольник АВС и любым из способов, постройте биссектрисы угла А и угла С, точка их

пересечения – точка О. Какую гипотезу можете выдвинуть о луче ВО? Докажите, что луч ВО — биссектриса треугольника АВС. Сформулируйте вывод о расположении всех биссектрис треугольника.3. Работа с моделью треугольника (5-7 минут). 1 вариант – остроугольный треугольник; 2 вариант – прямоугольный треугольник; 3 вариант – тупоугольный треугольник.

Учитель: на модели треугольника постройте две биссектрисы, обведите их жёлтым цветом. Обозначьте точку пересечения

биссектрис точкой К.Смотреть слайд № 1.4. Подготовка к основному этапу урока (10-13 минут).Учитель: начертите в тетради отрезок АВ. С помощью каких инструментов можно построить серединный перпендикуляр к отрезку? Определение серединного перпендикуляра. Два ученика выполняют на доскепостроение серединного перпендикуляра

(по заранее заготовленным моделям) двумя способами: линейкой, циркулем. Следующие два ученика устно доказывают утверждения:1. Каким свойством обладают точки серединногоперпендикуляра к отрезку?

2. Что можно сказать о точках равноудалённых от концовотрезка АВ?Учитель: начертите в тетрадипрямоугольный треугольник АВС и постройте серединные перпендикуляры к двум любым сторонам треугольника АВС.

Обозначьте точку пересечения О. Проведите перпендикуляр к третьей стороне через точку О. Что вы заметили? Докажите, что это серединный перпендикуляр к отрезку.5.

Работа смоделью треугольника (5 минут).Учитель: на модели треугольникапостройте серединные перпендикуляры к двум сторонам треугольника и обведите их зелёным цветом.

Обозначьте точку пересечения серединных перпендикуляров точкой О. Смотреть слайд № 2.

6. Подготовка к основному этапуурока (5-7 минут).Учитель: начертите тупоугольныйтреугольник АВС и постройте две высоты. Обозначьте их точку пересечения О.1. Что можно сказать о третьей высоте (третья высота,если её продолжить за основание, будет проходить через точку О)?

2. Как доказать, что все высоты пересекаются в однойточке?3. Какую новую фигуру образуют эти высоты и чем они в нейявляются?

7. Работа с моделью треугольника (5 минут).

Учитель: на модели треугольника постройте три высоты и обведите их синим цветом. Обозначьте точку пересечения высот точкой Н. Смотреть слайд № 3.

Урок второй

8. Подготовка к основному этапу урока (10-12 минут).Учитель: начертите остроугольный треугольник АВС и постройте все его медианы. Обозначьте их точку пересечения О. Какимсвойством обладают медианы треугольника?

9. Работа с моделью треугольника (5минут).Учитель: на модели треугольника постройте три медианы и обведите их коричневым цветом.

Обозначьте точку пересечения медиан точкой Т.Смотретьслайд № 4.10. Проверка правильности построения (10-15 минут).1. Что можно сказать о точке К? / ТочкаК-точка пересечения биссектрис, она равноудалена от всех сторон треугольника/

2. Покажите на модели расстояние от точки К долюбой стороны треугольника. Какую фигуру вы начертили? Как расположен этот

отрезок к стороне? Выделите жирно простым карандашом. (Смотреть слайд № 5).3. Чем является точка, равноудалённаяот трёх точек плоскости, не лежащих на одной прямой? Постройте жёлтым карандашом окружность с центром К и радиусом, равным выделенному простым карандашом расстоянию. (Смотреть слайд № 6).

4. Что вы заметили? Как расположена этаокружность относительно треугольника? Вы вписали окружность в треугольник. Как можно назвать такую окружность?

Учитель даёт определение вписанной окружности в треугольник. 5. Что можно сказать о точке О? ТочкаО –точка пересечения серединных перпендикуляров и она равноудалена от всех вершин треугольника . Какую фигуру можно построить, связав точки А,В,С и О?6. Постройте зелёным цветомокружность(О; ОА). (Смотреть слайд № 7).

7. Что вы заметили? Как расположена этаокружность относительно треугольника? Как можно назвать такую окружность? Как в таком случае можно назвать треугольник?

Учитель даёт определение описанной окружности около треугольника. 8. Приложите к точкам О,Н и Т линейку ипроведите красным цветом прямую через эти точки. Эта прямая называется прямой

Эйлера.( Смотреть слайд № 8).9. Сравните ОТ и ТН. Проверьте ОТ :ТН=1 : 2. (Смотреть слайд № 9).

10. а) Найдитемедианы треугольника (коричневым цветом). Отметьте чернилами основания медиан.

Где находятся эти три точки?б) Найдитевысоты треугольника (синим цветом). Отметьте чернилами основания высот. Сколько этих точек? 1 вариант-3; 2 вариант-2; 3 вариант-3.в) Измерьтерасстояния от вершин до точки пересечения высот. Назовите эти расстояния (АН,

ВН, СН). Найдите середины этих отрезков и выделите чернилами. Сколько таких

точек? 1 вариант-3; 2 вариант-2; 3 вариант-3. 11. Посчитайте, сколько получилосьточек, отмеченных чернилами? 1 вариант — 9; 2 вариант-5; 3 вариант-9. Обозначьте

точки D1 , D2 ,…, D9. (Смотреть слайд № 10).Через этиточки можно построить окружность Эйлера. Центр окружности точка Е находится в середине отрезка ОН. Строим красным цветом окружность (Е ; ЕD1). Эта окружность, как и прямая,названа именем великого учёного. (Смотреть слайд № 11). 11. Презентация об Эйлере (5 минут).12. Итог

Видео:№274. Докажите, что в равнобедренном треугольнике середина основания равноудалена от боковых сторон.Скачать

Ученический проект «Замечательные точки треугольника»

« ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ ТРЕУГОЛЬНИКА». ( Прикладные и фундаментальные вопросы математики) Баранова Елена 8 кл., МКОУ «СОШ № 20» Пос. Новоизобильный, Духанина Татьяна Васильевна, учитель математики МКОУ «СОШ №20» Посёлок Новоизобильный 2013. Муниципальное казённое общеобразовательное учреждение «Средняя общеобразовательная школа №20»

Цель: исследование треугольника на его замечательные точки, изучение их классификаций и свойств. Задачи: 1.Изучить необходимую литературу 2. Изучить классификацию замечательных точек треугольника 3.. Познакомиться со свойствами замечательных точек треугольника 4.

Уметь строить замечательные точки треугольника. 5. Изучить область применения замечательных точек. Объект исследования — раздел математики — геометрия Предмет исследования — треугольник Актуальность: расширить свои знания о треугольнике, свойствах его замечательных точек.

Гипотеза: связь треугольника и природы

Точка пересечения серединных перпендикуляров Она равноудалена от вершин треугольника и является центром описанной окружности. Окружности, описанные около треугольников, вершинами которых являются середины сторон треугольника и вершины треугольника пересекаются в одной точке, которая совпадает с точкой пересечения серединных перпендикуляров.

• Слайд 4
• Точка пересечения биссектрис Точка пересечения биссектрис треугольника равноудалена от сторон треугольника. ОМ=ОА=ОВ
• Слайд 5
• Точка пересечения высот Точка пересечения биссектрис треугольника, вершинами которого являются основания высот, совпадает с точкой пересечения высот треугольника.
• Слайд 6

Точка пересечения медиан Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

Если точку пересечения медиан соединить с вершинами, то треугольник разобьётся на три треугольника, равных по площади.

Важным свойством точки пересечения медиан является тот факт, что сумма векторов , началом которых является точка пересечения медиан, а концами – вершины треугольников, равна нулю М1 N C B А м2 м3 М1 N C B А м2 м3 М1 N C B А м2 м3 М1 N C B А м2 м3

1. Слайд 7
2. Точка Торричелли Замечание: точка Торричелли существует, если все углы треугольника меньше 120.
3. Слайд 8
4. Окружность девяти точек В1, А1, С1 – основания высот; А2, В2, С2 – середины соответствующих сторон; А3, В3, С3, — середины отрезков АН, ВН и СН.
5. Слайд 9
6. Прямая Эйлера Точка пересечения медиан, точка пересечения высот, центр окружности девяти точек лежат на одной прямой, которую называют прямой Эйлера в честь ученого математика определившего эту закономерность.
7. Слайд 10

Н емного из истории открытия замечательных точек В 1765 году Эйлер обнаружил, что середины сторон треугольника и основания его высот лежат на одной окружности.

Самым удивительным свойством замечательных точек треугольника является то, с что некоторые из них связаны друг с другом определённым соотношением.

Точка пересечения медиан М, точка пересечения высот Н, и центр описанной окружности О лежат на одной прямой, причём точка М делит отрезок ОН так, что справедливо соотношение ОМ : ОН = 1: 2. Эта теорема была доказана Леонардом Эйлером в 1765 году.

Связь геометрии с природой. В этом положении потенциальная энергия имеет наименьшее значение и сумма отрезков МА+МВ+МС будет наименьшей, а сумма векторов, лежащих на этих отрезках с началом в точке Торричелли, будет равна нулю.

Выводы Я узнала, что кроме известных мне замечательных точек пересечения высот, медиан, биссектрис и серединных перпендикуляров существуют еще замечательные точки и линии треугольника.

Полученные знания по данной теме смогу использовать в своей учебной деятельности, самостоятельно применять теоремы к определенным задачам, применять изученные теоремы в реальной ситуации. Считаю, что применение замечательных точек и линий треугольника в изучении математики является эффективным.

Знание их значительно ускоряет решение многих заданий. Предложенный материал можно использовать как на уроках математики, так и во внеклассных занятиях учащимися 5-9-х классов .

💥 Видео

Построение точки, равноудаленной от концов отрезковСкачать

Первая замечательная точка треугольникаСкачать

№949. На оси абсцисс найдите точку, равноудаленную от точек: а) А (1; 2)Скачать