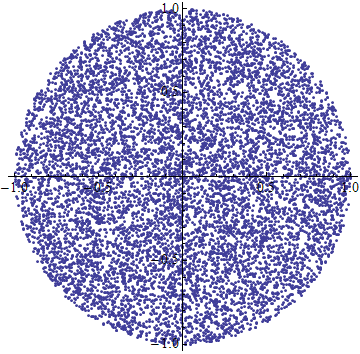
Равномерное распределение на окружности (8 видео)

Генерировать случайную точку внутри круга (равномерно)

Мне нужно создать равномерно случайную точку в пределах круга радиуса R.

Я понимаю, что просто выбирая равномерно случайный угол в интервале [0 . 2π) и равномерно случайный радиус в интервале (0 . R) Я бы закончил с большим количеством точек к центру, так как для двух заданных радиусов точки меньшего радиуса будут ближе друг к другу, чем для точек большего радиуса.

Я нашел запись в блоге это здесьЯ бы очень хотел понять, откуда он получает (2/R 2 )×r и как он получает окончательное решение.

обновление: через 7 лет после публикации этого вопроса я все еще не получил удовлетворительного ответа на фактический вопрос о математике алгоритма квадратного корня. Так я провел день сам пишу ответ. ссылка на мой ответ.

Содержание

21 ответов
как создать случайную точку в пределах круга радиуса R:
почему sqrt(random()) ?
Равномерное распределение на окружности
Создать случайную точку внутри круга (равномерно)
Как создать случайную точку внутри круга радиуса R :
Зачем sqrt(random()) ?
🎥 Видео

Видео:Равномерное распределениеСкачать

21 ответов

давайте как Архимед бы.

как мы можем генерировать точку равномерно в треугольнике ABC, где / AB / =|BC/? Давайте упростим это, распространившись на параллелограмм ABCD. Легко генерировать точки равномерно в ABCD. Мы равномерно выбираем случайную точку X на AB и Y на BC и выбираем Z такой, что XBYZ является параллелограммом. Чтобы получить равномерно выбранную точку в исходном треугольнике, мы просто складываем все точки, которые появляются в АЦП, обратно в ABC вдоль ПЕРЕМЕННЫЙ ТОК.

Теперь рассмотрим кругу. В пределе мы можем думать о нем как о бесконечном множестве изоцелевых треугольников ABC с B в начале и A и C на окружности, исчезающе близких друг к другу. Мы можем выбрать один из этих треугольников, просто выбрав угол тета. Поэтому теперь нам нужно сгенерировать расстояние от центра, выбрав точку в Щепке ABC. Опять же, распространитесь на ABCD, где D теперь вдвое больше радиуса от центра круга.

выбор случайной точки в ABCD используя описанный выше метод. Выберите случайную точку на AB. Равномерно выберите случайную точку на BC. То есть. выберите пару случайных чисел X и y равномерно на [0, R], дающих расстояния от центра. Наш треугольник представляет собой тонкую полоску, поэтому AB и BC по существу параллельны. Таким образом, точка Z-это просто расстояние x+y от начала координат. Если x+y>R, мы складываемся обратно.

вот полный алгоритм для R=1. Надеюсь, вы согласитесь, что все очень просто. Он использует trig, но вы можете дать гарантию на сколько времени он будет возьмите, а сколько random() вызывает его потребности, не похож на забор сброса.

вот он в Mathematica.

Видео:Равномерное распределение по кругу текста вдоль пути. Создание часов в Corel Draw от ДеревяшкинаСкачать

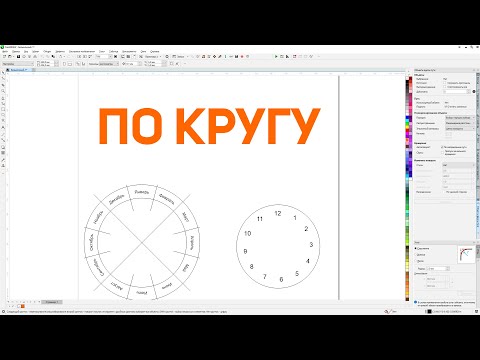
как создать случайную точку в пределах круга радиуса R:

(если random() дает значение между 0 и 1 равновероятно)

если вы хотите преобразовать это в Декартовые координаты, вы можете сделать

Видео:Равномерное распределение случайной величиныСкачать

почему sqrt(random()) ?

давайте посмотрим на математику, которая приводит к sqrt(random()) . Предположим для простоты, что мы работаем с единичным кругом, т. е. R = 1.

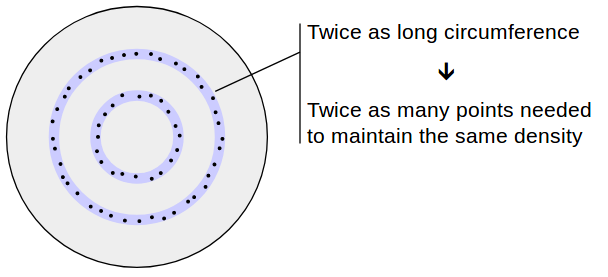
среднее расстояние между точками должно быть одинаковым независимо от того, как далеко от центра мы смотрим. Это означает, например, что, глядя на периметр круга с окружностью 2, мы должны найти в два раза больше точек, чем количество точек на периметре круга с окружностью 1.

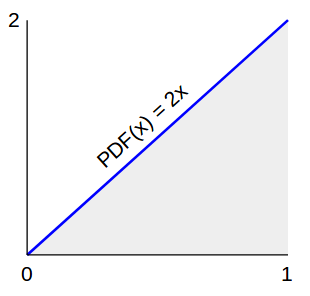
С длины окружности (2πr) растет линейно с r, из этого следует, что количество случайных точек должно линейно расти с r. Другими словами, желаемое функция плотности вероятности (PDF) растет линейно. Поскольку PDF должен иметь площадь равную 1, а максимальный радиус равен 1, то есть

таким образом, мы знаем, как должна выглядеть желаемая плотность наших случайных значений. Теперь:как мы генерируем такое случайное значение, когда все мы имеют равномерное случайное значение между 0 и 1?

из PDF создайте кумулятивная функция распределения (CDF)
зеркало это вдоль y = x
применить полученную функцию к равномерному значению от 0 до 1.

звучит сложно? Позвольте мне вставить желтую коробку с небольшим количеством боковой путь, который передает интуицию:

Предположим, мы хотим создать случайную точку со следующим распределением:

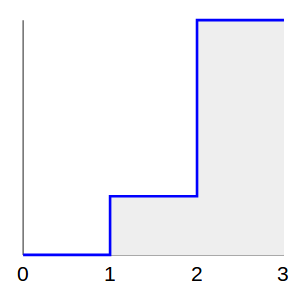
1/5 из пунктов равномерно между 1 и 2, и
4/5 точек равномерно между 2 и 3.

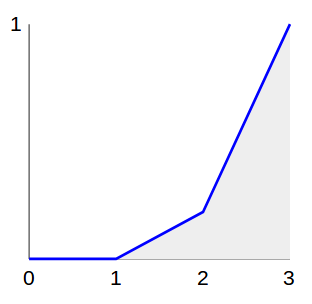
CDF, как следует из названия, является накопительной версией PDF. Интуитивно: Пока PDF (x) описывает количество случайных значений на x, CDF (x) описывает количество случайных значений меньше, чем x.

в этом случае CDF будет выглядеть так:

чтобы увидеть, как это полезно, представим, что мы стреляем пулями слева направо на равномерно распределенных высот. Когда пули попадают в линию, они падают на землю:—10—>

посмотрите, как плотность пуль на земле соответствует нашему желаемому распределению! Мы почти на месте!

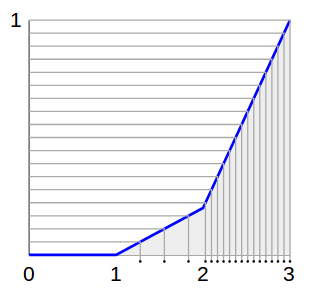
проблема в том, что для этой функции y ось —выход и x ось —вход. Мы можем только «стрелять пулями с земли прямо вверх»! Нам нужна обратная функция!

вот почему мы отражаем все это; x становится y и y становится x:

мы называем это CDF -1 . Чтобы получить значения в соответствии с желаемым распределением, мы используем CDF -1 (random ()).

. Итак, вернемся к генерации случайных значений радиуса, где наш PDF равен 2x.

Шаг 1: Создайте CDF:

Поскольку мы работаем с reals, CDF выражается как Интеграл PDF.

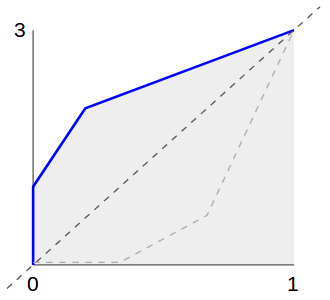
Шаг 2: Зеркало CDF вдоль y = x:

математически это сводится к замене x и y и решения для y:

Шаг 3: примените полученную функцию к равномерному значению между 0 и 1

CDF -1 (random ()) = √random ()

что мы намеревались вывести: -)

вот быстрое и простое решение.

выбрать два случайных числа в диапазоне (0, 1), а именно a и b . Если b , поменять их местами. Ваша точка зрения (b*R*cos(2*pi*a/b), b*R*sin(2*pi*a/b)) .

вы можете думать об этом решении следующим образом. Если взять круг, вырезать его, а затем выпрямить, получится прямоугольный треугольник. Масштабируйте этот треугольник вниз, и у вас будет треугольник из (0, 0) до (1, 0) to (1, 1) и (0, 0) . Все эти преобразования измените плотность равномерно. То, что вы сделали, — это равномерно выбрать случайную точку в треугольнике и обратить процесс, чтобы получить точку в круге.

обратите внимание на плотность точки пропорционально обратному квадрату радиуса, следовательно, вместо выбора r С [0, r_max] С [0, r_max^2] , затем вычислите свои координаты как:

это даст вам равномерное распределение точек на диске.

подумайте об этом таким образом. Если у вас есть прямоугольник, где одна ось-радиус, а одна-угол, и вы берете точки внутри этого прямоугольника, которые находятся рядом с радиусом 0. Все они будут падать очень близко к началу (то есть близко друг к другу по кругу.) Однако точки вблизи радиуса R все они будут падать вблизи края круга (то есть далеко друг от друга.)

Это может дать вам некоторое представление о том, почему вы получаете такое поведение.

фактор это выведено на этой ссылке говорит вам, сколько соответствующей области в прямоугольнике необходимо настроить, чтобы не зависеть от радиуса, как только он сопоставлен с кругом.

Edit: Итак, то, что он пишет в ссылке, которую вы разделяете, — «это достаточно легко сделать, вычисляя обратное кумулятивное распределение, и мы получаем для r:».

основная предпосылка здесь заключается в том, что вы можете создать переменную с желаемым распределением из равномерного, сопоставив равномерное обратным функция кумулятивной функции распределения желаемой функции плотности вероятности. Почему? Просто примите это как должное, но это факт.

вот мой somehwat интуитивное объяснение математики. Функция плотности f (r) по отношению к r должна быть пропорциональна самой r. Понимание этого факта является частью любой основной книги по исчислению. См. разделы об элементах полярной области. Некоторые другие плакаты упоминали об этом.

поэтому мы назовем его f (r) = C*r;

это, оказывается, большая часть работы. Теперь, поскольку F(r) должна быть плотностью вероятности, вы можете легко увидеть,что, интегрируя f (r) через интервал (0, R), вы получите, что C = 2/R^2 (это упражнение для читателя.)

таким образом, f(r) = 2*r/r^2

OK, так вот как вы получаете формулу в ссылке.

тогда конечная часть идет от равномерной случайной величины u в (0,1), которую вы должны отобразить обратной функцией кумулятивного функция распределения от этой желаемой плотности f (r). Чтобы понять, почему это так, вам нужно найти расширенный текст вероятности, такой как Papoulis, вероятно (или вывести его самостоятельно.)

интегрируя f (r), вы получаете F(r) = r^2/R^2

чтобы найти обратную функцию этого, вы устанавливаете u = r^2 / R^2, а затем решаете для r, что дает вам r = R * sqrt (u)

это полностью имеет смысл интуитивно тоже, u = 0 должно соответствовать r = 0. Кроме того, U = 1 shoudl map to r = R. Также, он идет по функции квадратного корня, которая имеет смысл и соответствует ссылке.

Это действительно зависит от того, что вы подразумеваете под ‘абсолютно случайная’. Это тонкий момент, и вы можете прочитать больше об этом на странице wiki здесь:http://en.wikipedia.org/wiki/Bertrand_paradox_%28probability%29, где одна и та же проблема, давая разные интерпретации «равномерно случайным» дает разные ответы!

в зависимости от того, как вы выбираете точки, распределение может варьироваться, даже если они равномерно случайны в некоторые чувство.

похоже, что запись в блоге пытается сделать ее равномерно случайной в следующем смысле: если вы берете подпругу круга с тем же центром, то вероятность того, что точка падает в этой области, пропорциональна площади области. Это, я считаю, пытается следовать теперь стандартной интерпретации «равномерно случайных» для 2D-областей с области, определенные на них: вероятность падения точки в любой области (с областью хорошо defined) пропорциональна площади этой области.

причина, по которой наивное решение не работает, заключается в том, что оно дает более высокую плотность вероятности точкам ближе к центру круга. Другими словами, окружность с радиусом r/2 имеет вероятность r/2 получить выбранную в ней точку, но имеет площадь (количество точек) pi*r^2/4.

поэтому мы хотим, чтобы плотность вероятности радиуса имела следующее свойство:

вероятность выбора радиуса меньшего или равного заданному r должна быть пропорциональна площадь окружности с радиусом r. (потому что мы хотим иметь равномерное распределение по точкам, а большие площади означают больше точек)

другими словами, мы хотим, чтобы вероятность выбора радиуса между [0, r] была равна его доле от общей площади круга. Общая площадь окружности равна pi * R^2, а площадь окружности с радиусом r равна pi * r^2. Таким образом,мы хотели бы, чтобы вероятность выбора радиуса между [0, r] была (pi*r^2)/(pi*R^2) = r^2/R^2.

теперь приходит математика:

вероятность выбора радиуса между [0, r] является интегралом от p(r) dr от 0 до r (это просто потому, что мы добавляем все вероятности меньших радиусов). Таким образом, мы хотим Интеграл(p(r)dr) = r^2/R^2. Мы можем ясно видеть, что R^2 является константой, поэтому все, что нам нужно сделать, это выяснить, какой p(r), когда он интегрирован, даст нам что-то вроде r^2. Ответ явно Р * постоянный. Интеграл (R * константа dr) = r^2/2 * константа. Это должно быть равно r^2/R^2, поэтому Константа = 2 / R^2. Таким образом, у вас есть распределение вероятностей p(r) = r * 2/R^2

Примечание:

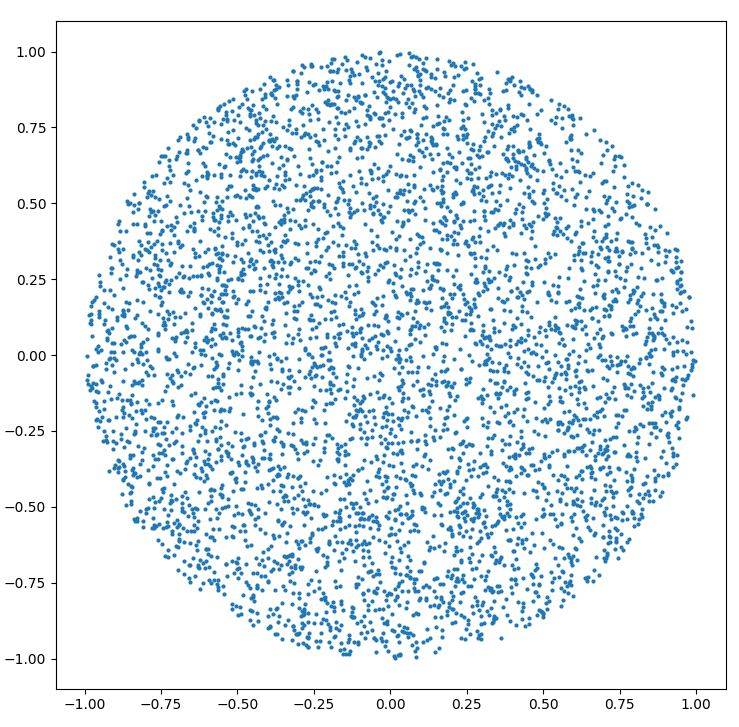
вот мой код Python для генерации num случайные точки из окружности радиуса rad :

пусть ρ (радиус) и φ (Азимут) — две случайные величины, соответствующие полярным координатам произвольной точки внутри круга. Если точки распределены равномерно, то какова функция распределения ρ и φ?

где S1 и S0-площади круга радиус r и R соответственно. Таким образом, CDF можно дать как:

обратите внимание, что для r=1 случайная величина sqrt(X), где X равномерна на [0, 1), имеет этот точный CDF (потому что P[sqrt(X)

распределение φ, очевидно, равномерно от 0 до 2*π. Теперь вы можете создавать случайные полярные координаты и преобразовывать их в Декартовые, используя тригонометрические уравнения:

не могу сопротивляться сообщение кода python для R=1.

вы получите

Видео:Нормальное Распределение за 6 МинутСкачать

Равномерное распределение на окружности

Статистика первых цифр степеней двойки
и передел мира

Доклад, прочитанный акад. В.И. Арнольдом
в Университете Торонто (Канада) 9 июня 1997 г.

Первая цифра числа 2 n бывает единицей примерно в 6 раз чаще, чем девяткой. Так же распредеделены первые цифры населений и площадей стран мира. Предлагаемое ниже объяснение этого факта приводит к большому количеству математических гипотез, часть из которых доказана, а часть лишь подтверждена компьютерными экспериментами и ожидает строгого доказательства.

Последовательность первых цифр чисел 2 n ( n = 0, 1, 2. ) начинается с

1, 2, 4, 8, 1, 3, 6, 1, 2, 5, 1.

Можно проверить, продолжив вычисление, что единицы составляют примерно 30% членов этой последовательности (а девятка — меньше 5%). Такое же распределение получается для последовательности первых цифр чисел 3 n и вообще для почти любой геометрической прогрессии. (Очевидное исключение составляют лишь прогрессии со знаменателями 10, 10 1/2 и вообще 10 p/q , где p и q целые.)

Доказательство сформулированного удивительного утверждения получено Г.Вейлем почти 100 лет назад. Он доказал даже больше. Напомню, что каждое действительное число c можно представить единственным образом в виде суммы целого числа (называемог о целой частью числа c ) и дробной доли , принадлежащей интервалу [0, 1]).

Теорема. Пусть x — иррациональное число. Тогда последовательность дробных долей чисел nx (n = 0, 1, 2. ) равномерно распределена на интервале (0, 1).

Это значит, что число значений n , 0 ? n , для которых дробная доля nx принадлежит любому фиксированному отрезку длиной a , поделенное на N , стремится к a при N , стремящемся к бесконечности.

Иными словами, рассмотрим движение точки по окружности, в котором точка в целые моменты времени ( n ) перескакивает вперед на (несоизмеримый с 2 p ) угол 2 p x (рис.1). Теорема утверждает, что время, проведенное движущейся точкой на любой дуге окружности, асимтотически (при большом времени наблюдения) пропорционально длине дуги (и не зависит ни от положения дуги на окружности, ни от начальной точки, ни даже от величины угла поворота).

Рис. 1. Траектория точки при итерации проворота окружности

Распределение первых цифр чисел 2 n получается теперь следующим образом. Рассмотрим последовательность чисел lg(2 n ) = nx . Число x = lg 2 иррационально (здесь и далее lg — логарифм по основанию 10). По теореме последовательность дробных долей чисел nx равномерно распределена на интервале (0, 1).

Но первая цифра i числа 2 n определяется тем, в какой из интервалов между числами lg( i + 1) и lg( i ) попадает дробная доля числа lg(2 n ). По теореме, доли чисел 2 n , начинающихся с i ( = 1, 2, . 9) составляют p i = lg( i + 1) – lg i . Например, для первой цифры i = 1 эта доля составляет lg(2) = 0,301 (близость этого логарифма к 3/10 отражает близость 2 10 = 1024 к 1000 = 10 3 . Поэтому доля единиц среди первых цифр чисел составляет примерно 30%. Доли всех цифр (в процентах) даются таблицей 1.

Девяток примерно в 6 раз меньше, чем единиц (рис.2).

Рис. 2. Распределение первых цифр степени двойки

Из всего сказанного для дальнейшего важен такой вывод: приведенное в таблице странно неравномерное распределение первых цифр чисел последовательности объясняется равномерным распределением дробных долей логарифмов чисел нашей последовательности.

Этот вывод приводит к одинаковому распределению первых цифр для многих различных последовательностей (например, для геометрических прогрессий или , но не только для них).

Население стран мира

Лет двадцать назад Н.Н.Константинов сообщил мне, что первые цифры населений стран мира распределены так же, как первые цифры степеней двойки (табл. 2).

Вот мое тогдашнее объяснение этого факта.

Согласно теории Мальтуса, население каждой страны растет в геометрической прогрессии. Из теоремы Вейля (см. предыдущий раздел) следует, что первые цифры населения фиксированной страны в последовательные годы распределены как первые цифры степеней двойки (см. рис.2). Согласно “эргодической теореме” (или, лучше сказать, согласно эргодическому принципу), временное среднее можно заменить пространственным: распределение по странам в один и тот же год должно совпадать с распределением в одной стране в разные годы.

Для контроля теории я рассмотрел числа страниц в книгах моей библиотеки, длины рек и высоты гор. Во всех этих случаях доли единиц и доли девяток среди первых цифр полученных чисел оказались практически одинаковыми: p i = 1/9. Книги, реки и горы не растут в геометрической прогрессии, теория Мальтуса к ним не применима. Поэтому различие статистик первых цифр в числах, выражающих населения и, скажем, длины рек, служит своеобразным косвенным подтверждением формулы Мальтуса (согласно которой население растет в геометрической прогрессии).

Однако лет десять назад М.Б.Севрюк обнаружил, что не только населения, но и площади стран мира подчиняются такому же закону распределения первых цифр, как степени двойки! К площадям теория Мальтуса, по-видимому, неприменима, так что возник вопрос — как объяснить это поведение площадей. Ниже я пытаюсь дать ответ на этот вопрос.

Площади стран мира

Предыдущие примеры подсказывают, что следует искать причину странного распределения первых цифр площадей стран мира либо в их росте, либо в убывании (в геометрической прогрессии). История мира показывает, что площади стран (особенно империй) иногда растут, а иногда убывают за счет то присоединения одних стран к другим, то распада. Рассмотрим вначале самую примитивную модель этого явления. Предположим, что за единицу времени страна с вероятностью половина делится пополам, а с вероятностью половина присоединяет к себе другую страну такой же площади, как она сама.

Теорема. Распределение дробных долей логарифмов площадей, занимаемых такой случайной страной в момент n, стремится к равномерному распределению на интервале
(0, 1) при n, стремящемся к бесконечности.

Иными словами, вероятность того, что первая цифра площади окажется единицей, стремится при n ® ? к lg(2) = 0,3,01, . что она окажется девяткой — примерно к 0,046.

Действительно, рассмотрим последовательность l n = lgS(n), где S — площадь в момент n. Точка в следующий момент n + 1 с одинаковой вероятностью сдвигается влево или вправо на lg 2 (причем, конечно, выбор, что делать — делиться или объединяться, — в каждый момент времени независим от выбора в другие моменты времени). По законам теории вероятностей, распределение величины l n при больших n будет в основном сосредоточено на отрезке большой (порядка n 1/2 ) длины и будет пологим и симметричным (рис.3). При переходе к дробным долям (т.е. при “наматывании оси l на окружность l mod 1”) из такого распределения на оси l получится почти равномерное (при больших n ) распределение на окружности (детали обоснования предоставляются читателю; важно, что последовательность дробных долей чисел mlg(2) распределена равномерно).

Рис. 3. При наматывании прямой с пологим распределением на окружность
на ней получается почти равномерное распределение.

Имеется множество более сложных моделей передела мира, приводящих в численных экспериментах к такому же эффекту. Вероятно, для целых классов таких моделей можно строго доказать предельную равномерность распределения дробных долей логарифмов площадей стран. Вот несколько примеров.

1. В начальный момент имеется k стран площадей S 1 , . S k . В каждый последующий момент одна (случайно выбираемая) страна с вероятностью 50% делится, а с вероятностью 50% объединяется с какой-либо (случайно выбранной) страной. Разумеется, выборы, делаемые в разные моменты времени, считаются независимыми и все случайно выбираемые страны равновероятны.

По вычислениям М.В.Хесиной (университет Торонто, июнь 1997) при S i = i, k = 100 распределение первых цифр площадей стран становится практически таким же, как приведенное выше распределение первых цифр степеней двойки, уже через сотню шагов.

2. Введение деления на неравные части с каким-либо законом распределения частей (например, равномерным) приводит к такому же результату.

3. В моделях, где разрешается объединяться лишь с соседями, устанавливается такое же распределение первых цифр. Например, в одной из моделей Ф.Аикарди (Триест, июнь 1997) страны представлялись дугами окружности, а площади — длинами этих дуг. Распределение, практически неотличимое от распределения первых цифр степеней двойки, наступает очень быстро.

4. В другой модели Аикарди мир представляется графом, задающим разбиение сферы на треугольники ( n вершин которых представляют n стран и снабжены “площадями”, распределенными на интервале (1, n ) по закону случая). Граф строится, начиная с икосаэдра, при помощи итераций такой операции: случайно выбирается треугольная грань, добавляется вершина в ее центре и соединяется со всеми тремя вершинами грани.

Рис. 4. Отделение новой страны j от страны i

Во втором случае случайно выбирается соседняя с i вершина j и затем страны i и j объединяются (причем на графе исчезает ребро ij и две разделенные им треугольные грани, рис. 5).

Рис. 5. Слияние стран j и i

В трех экспериментах A,B,C были выбраны следующие значения параметров (табл. 3).

Средние (по 50 повторениям эксперимента с разными начальными условиями) значения долей единиц. девяток среди первых цифр площадей стран оказались такими (табл. 4; в последней строке ( D ) указаны частоты первых цифр степеней двойки).

Было бы интересно не только доказать общую теорему, указывающую область применимости равномерного распределения дробных долей логарифмов, но и проверить, подчиняются ли этому распределению, например, размеры компаний и их доходы.

Появление странного распределения первых цифр во многих различных ситуациях неоднократно обсуждалось в литературе. Однако я нигде не встречал каких-либо математических теорем или гипотез (подобных приведенным в настоящей статье), обосновывающих неизбежность появления этого распределения (исключая, разумеется, теорему Вейля).

Видео:Равномерное распределение точек в кругуСкачать

Создать случайную точку внутри круга (равномерно)

Мне нужно создать равномерно случайную точку в радиусе круга R .

Я понимаю это, просто выбирая равномерно случайный угол в интервале [0 . 2π) и равномерно случайный радиус в интервале (0 . R ), я получу больше точек к центру, поскольку для двух данных радиусы, точки в меньшем радиусе будут ближе друг к другу, чем для точек в большем радиусе.

Я нашел запись в блоге по этому поводу здесь , но я не понимаю его рассуждения. Я полагаю, это правильно, но мне бы очень хотелось понять, откуда он получает (2 / R 2 ) × r и как он получает окончательное решение.

Обновление: 7 лет после публикации этого вопроса я все еще не получил удовлетворительного ответа на фактический вопрос относительно математики позади алгоритма квадратного корня. Так что я потратил день на написание ответа сам. Ссылка на мой ответ .

Давайте подойдем к этому, как Архимед.

Как мы можем сгенерировать точку равномерно в треугольнике ABC, где | AB | = | BC |? Давайте сделаем это проще, расширив параллелограмм ABCD. В ABCD легко генерировать точки равномерно. Мы равномерно выбираем случайную точку X на AB и Y на BC и выбираем Z таким, что XBYZ является параллелограммом. Чтобы получить равномерно выбранную точку в исходном треугольнике, мы просто складываем любые точки, которые появляются в АЦП, обратно в АВС вдоль АС.

Теперь рассмотрим круг. В пределе мы можем рассматривать его как бесконечно много равнобедренных треугольников ABC с B в начале координат и A и C на окружности, исчезающе близко друг к другу. Мы можем выбрать один из этих треугольников, просто выбрав угол тета. Итак, теперь нам нужно сгенерировать расстояние от центра, выбрав точку в полоске ABC. Снова продлим до ABCD, где D теперь в два раза больше радиуса от центра круга.

Выбрать случайную точку в ABCD легко, используя описанный выше метод. Выберите случайную точку на AB. Равномерно выбрать случайную точку на BC. То есть. Выберите пару случайных чисел x и y равномерно на [0, R], давая расстояния от центра. Наш треугольник является тонкой полоской, поэтому AB и BC по существу параллельны. Таким образом, точка Z — это просто расстояние x + y от начала координат. Если x + y> R, мы сбрасываем обратно.

Вот полный алгоритм для R = 1. Я надеюсь, вы согласны, что это довольно просто. Он использует триггер, но вы можете дать гарантию того, сколько времени это займет и сколько random() вызовов ему нужно, в отличие от выборки отклонения.

Вот это в Mathematica.

Видео:Математика это не ИсламСкачать

Как создать случайную точку внутри круга радиуса R :

(Предполагается, что random() дает значение между 0 и 1 равномерно)

Если вы хотите преобразовать это в декартовы координаты, вы можете сделать

Видео:Равномерное распределение объектов по кругу (кривой) в панели макросов для Corel Draw от ДеревяшкинаСкачать

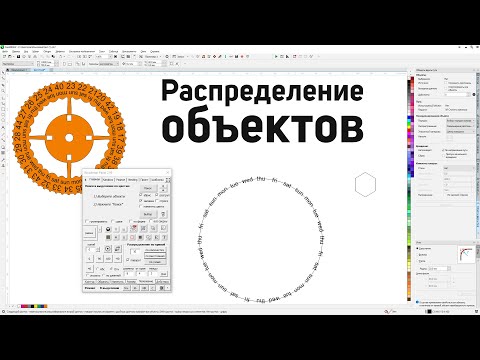
Зачем sqrt(random()) ?

Давайте посмотрим на математику, которая приводит к sqrt(random()) . Предположим для простоты, что мы работаем с единичным кругом, т.е. R = 1.

Среднее расстояние между точками должно быть одинаковым независимо от того, как далеко от центра мы смотрим. Это означает, например, что, глядя на периметр окружности с окружностью 2, мы должны найти вдвое больше точек, чем количество точек на периметре окружности с окружностью 1.

Поскольку окружность круга (2π r ) растет линейно с ростом r , отсюда следует, что число случайных точек должно расти линейно с ростом r . Другими словами, искомая функция плотности вероятности (PDF) растет линейно. Так как PDF должен иметь площадь, равную 1, а максимальный радиус равен 1, мы имеем

Итак, мы знаем, как должна выглядеть желаемая плотность наших случайных значений. Теперь: как мы можем генерировать такое случайное значение, когда все, что у нас есть, это равномерное случайное значение между 0 и 1?

Из PDF создайте накопительную функцию распределения (CDF)
Отразите это вдоль y = x
Примените полученную функцию к равномерному значению от 0 до 1.

Звучит сложно? Позвольте мне вставить цитату с небольшой боковой дорожкой, которая передает интуицию:

Предположим, мы хотим сгенерировать случайную точку со следующим распределением:

1/5 баллов равномерно между 1 и 2, и
4/5 баллов равномерно между 2 и 3.

CDF — это, как следует из названия, кумулятивная версия PDF. Интуитивно понятно: в то время как PDF ( x ) описывает количество случайных значений в точке x , CDF ( x ) описывает количество случайных значений меньше значения x .

В этом случае CDF будет выглядеть так:

Чтобы увидеть, как это полезно, представьте, что мы стреляем пулями слева направо на равномерно распределенных высотах. Когда пули попадают в линию, они падают на землю:

Посмотрите, как плотность пуль на земле соответствует нашему желаемому распределению! Мы почти там!

Проблема в том, что для этой функции ось y является выходной, а ось x является входной . Мы можем только «стрелять пулями прямо с земли»! Нам нужна обратная функция!

Вот почему мы отражаем все это; х становится у, а у становится х :

Мы называем это CDF -1 . Чтобы получить значения в соответствии с желаемым распределением, мы используем CDF -1 (random ()).

… Итак, вернемся к генерации случайных значений радиуса, где наш PDF равен 2 х .

Шаг 1: Создайте CDF: так

как мы работаем с реалами, CDF выражается как интеграл PDF.

Шаг 2: Зеркально отразите CDF вдоль y = x :

Математически это сводится к обмену x и y и решению для y :

Шаг 3: применить полученную функцию к равномерному значению от 0 до 1

CDF -1 (random ()) = √random ()

Что мы и собираемся извлечь 🙂

Вот быстрое и простое решение.

Выберите два случайных числа в диапазоне (0, 1), а именно a и b . Если b поменять их. Ваша точка зрения (b*R*cos(2*pi*a/b), b*R*sin(2*pi*a/b)) .

Вы можете думать об этом решении следующим образом. Если вы возьмете круг, обрежете его, а затем выпрямите, вы получите прямоугольный треугольник. Уменьшите этот треугольник, и вы получите треугольник от (0, 0) до (1, 0) до (1, 1) и обратно до (0, 0) . Все эти преобразования изменяют плотность равномерно. То, что вы сделали, равномерно выбрали случайную точку в треугольнике и полностью изменили процесс, чтобы получить точку в круге.

Обратите внимание на плотность точек пропорционально обратному квадрату радиуса, поэтому вместо того, чтобы выбирать r из [0, r_max] , выберите из [0, r_max^2] , а затем вычислите ваши координаты как:

Это даст вам равномерное распределение точек на диске.

Подумайте об этом таким образом. Если у вас есть прямоугольник, где одна ось является радиусом, а другая — углом, и вы берете точки внутри этого прямоугольника, которые близки к радиусу 0. Все они будут располагаться очень близко к началу координат (то есть близко друг к другу на окружности.) Однако, точки около радиуса R, все они будут падать около края круга (то есть далеко друг от друга).

Это может дать вам некоторое представление о том, почему вы получаете такое поведение.

Коэффициент, полученный по этой ссылке, говорит вам, сколько соответствующей области в прямоугольнике нужно отрегулировать, чтобы она не зависела от радиуса после его сопоставления с окружностью.

Редактировать: Итак, он пишет в ссылке, которой вы делитесь: «Это достаточно легко сделать, рассчитав обратное кумулятивному распределению, и мы получим для r:».

Основным условием здесь является то, что вы можете создать переменную с желаемым распределением из униформы, отобразив униформу с помощью обратной функции кумулятивной функции распределения желаемой функции плотности вероятности. Зачем? Просто пока принимайте это как должное, но это факт.

Вот мое интуитивное объяснение математики. Функция плотности f (r) по отношению к r должна быть пропорциональна самой r. Понимание этого факта является частью любой основной книги исчисления. Смотрите разделы об элементах полярной зоны. Некоторые другие постеры упоминали об этом.

Поэтому мы назовем это f (r) = C * r;

Это оказывается большая часть работы. Теперь, поскольку f (r) должна быть плотностью вероятности, вы можете легко увидеть, что, интегрируя f (r) по интервалу (0, R), вы получите, что C = 2 / R ^ 2 (это упражнение для читателя .)

Таким образом, f (r) = 2 * r / R ^ 2

Хорошо, вот как вы получите формулу в ссылке.

Затем последняя часть идет от равномерной случайной величины u в (0,1), которую необходимо отобразить с помощью обратной функции кумулятивной функции распределения от этой требуемой плотности f (r). Чтобы понять, почему это так, вам нужно найти расширенный вероятностный текст, такой как, вероятно, папулис (или получить его самостоятельно).

Интегрируя f (r), вы получите F (r) = r ^ 2 / R ^ 2

Чтобы найти обратную функцию этого, вы устанавливаете u = r ^ 2 / R ^ 2, а затем решаете для r, что дает вам r = R * sqrt (u)

Это также имеет смысл интуитивно, u = 0 должно отображаться на r = 0. Кроме того, u = 1 должно отображаться на r = R. Кроме того, оно идет по функции квадратного корня, которая имеет смысл и соответствует ссылке.

Причина, по которой наивное решение не работает, заключается в том, что оно дает более высокую плотность вероятности точкам, расположенным ближе к центру круга. Другими словами, у круга, который имеет радиус r / 2, есть вероятность r / 2 получить выбранную точку, но у него есть область (количество точек) pi * r ^ 2/4.

Поэтому мы хотим, чтобы плотность вероятности радиуса имела следующее свойство:

Вероятность выбора радиуса, меньшего или равного данному r, должна быть пропорциональна площади круга с радиусом r. (потому что мы хотим иметь равномерное распределение по точкам, а большие области означают больше точек)

Другими словами, мы хотим, чтобы вероятность выбора радиуса между [0, r] была равна его доле от общей площади круга. Общая площадь круга равна pi * R ^ 2, а площадь круга с радиусом r равна pi * r ^ 2. Таким образом, мы хотели бы, чтобы вероятность выбора радиуса между [0, r] была (pi * r ^ 2) / (pi * R ^ 2) = r ^ 2 / R ^ 2.

Теперь приходит математика:

Вероятность выбора радиуса между [0, r] является интегралом p (r) dr от 0 до r (это просто потому, что мы добавляем все вероятности меньших радиусов). Таким образом, мы хотим, чтобы интеграл (p (r) dr) = r ^ 2 / R ^ 2. Мы можем ясно видеть, что R ^ 2 является константой, поэтому все, что нам нужно сделать, это выяснить, какой p (r) при интеграции даст нам что-то вроде r ^ 2. Ответ явно г * постоянный. интеграл (r * постоянная dr) = r ^ 2/2 * постоянная. Это должно быть равно r ^ 2 / R ^ 2, поэтому константа = 2 / R ^ 2. Таким образом, у вас есть распределение вероятности p (r) = r * 2 / R ^ 2

Примечание. Другой, более интуитивно понятный способ осмыслить проблему — представить, что вы пытаетесь присвоить каждому кругу радиус вероятности плотности ra, равный пропорции числа точек на его окружности. Таким образом, окружность с радиусом r будет иметь 2 * pi * r «точки» на своей окружности. Общее количество баллов: pi * R ^ 2. Таким образом, вы должны дать окружности ra вероятность, равную (2 * pi * r) / (pi * R ^ 2) = 2 * r / R ^ 2. Это намного проще для понимания и более интуитивно понятно, но не совсем математически обоснованно.

Пусть ρ (радиус) и φ (азимут) — две случайные величины, соответствующие полярным координатам произвольной точки внутри окружности. Если точки распределены равномерно, то какова функция распределения ρ и φ?

Для любого r: 0 2

Где S1 и S0 — площади круга радиуса r и R соответственно. Таким образом, CDF может быть дан как:

Обратите внимание, что для R = 1 случайная величина sqrt (X), где X равномерно на [0, 1), имеет этот точный CDF (потому что P [sqrt (X) — англичанин, иммигрировавшие в Австралии
источник

Это действительно зависит от того, что вы подразумеваете под «равномерно случайным». Это тонкий момент, и вы можете узнать больше об этом на странице вики здесь: http://en.wikipedia.org/wiki/Bertrand_paradox_%28probability%29 , где та же проблема, давая различные интерпретации для «равномерно случайных» дает разные ответы!

В зависимости от того, как вы выбираете точки, распределение может варьироваться, даже если они в некоторых смысле .

Кажется, что запись в блоге пытается сделать ее равномерно случайной в следующем смысле: если вы возьмете под круг окружности с тем же центром, то вероятность того, что точка попадет в эту область, пропорциональна площади область. Я полагаю, что это попытка следовать принятой в настоящее время стандартной интерпретации «равномерно случайных» для 2D-областей с определенными на них областями : вероятность падения точки в любом регионе (с четко определенной областью) пропорциональна площади этого региона.