Равнобокая трапеция описана около окружности основания трапеции равны 2

Равнобокая трапеция описана около окружности. Основания трапеции равны 2 и 8. найдите радиус вписанной окружности. Вc+ad=10. AB+DC=10. 2. 2. С. В. 4. А. D. 8.

Слайд 9 из презентации «Вписанная и описанная»

Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию «Вписанная и описанная.ppt» можно в zip-архиве размером 526 КБ.

Видео:Трапеция. Практическая часть - решение задачи. 8 класс.Скачать

Вписанная и описанная окружность

«Задачи на вписанную окружность» — Центр вписанной в треугольник окружности. Капитан. Радиус. Тесты. Конкурс капитанов. Чёрный ящик. Готовые чертежи. Вписанные окружности. Возможные ответы. Художник. Вписанная окружность. Циркуль. Полупериметр. Полупериметр многоугольника. Решение.

«Радиус вписанной и описанной окружности» — Окружность и правильные многоугольники. Окружность. Описанная окружность. Окружность и треугольники. Окружность и прямоугольный треугольник. Выпуклый многоугольник. Описанная окружность около четырёхугольника. Параллелограмм. Трапеция. Основные формулы для правильных многоугольников. Вписанная окружность в четырёхугольник.

«Вписанная окружность» — Вписанная окружность. 2) Не во всякий четырехугольник можно вписать окружность. Задача № 1. Замечания: В треугольник можно вписать только одну окружность! Доказательство: Теорема: В любой треугольник можно вписать окружность. Задача № 2. В любом описанном четырехугольнике суммы противоположных сторон равны.

«Задачи по вписанной и описанной окружности» — Можно ли описать окружность около правильного многоугольника. Около всякого треугольника можно описать окружность. Укажите центр окружности, описанной около треугольника. Около трапеции описана окружность. Около любого правильного многоугольника можно описать окружность. Гипотенуза прямоугольного треугольника.

«Описанная окружность» — Окружность называется описанной около многоугольника, если… Диаметр? Треугольники и окружность. Многоугольник называется описанным около окружности, если … Четырехугольник и окружность. Сколько окружностей можно вписать в треугольник? Четырехугольники. Описанный многоугольник. Вписанная окружность. Центровики.

«Формулы описанной и вписанной окружности» — Устная работа. Вершины треугольника. Высота. Суммы длин противолежащих сторон. Окружность. Углы вписанного четырехугольника. Треугольник. Выберите верное утверждение. Работа с учебником. Закончите предложение. Центр окружности. Точка пересечения. Вписанная и описанная окружности. Центр описанной окружности.

Видео:Геометрия Около окружности радиуса √2 описана равнобедренная трапеция, у которой одно основаниеСкачать

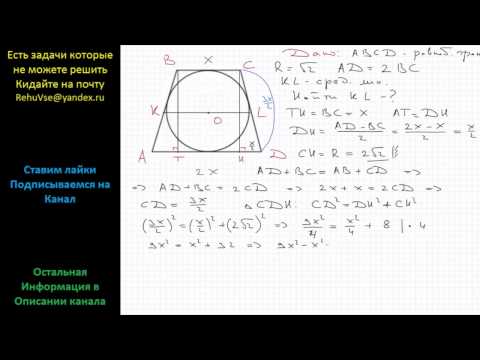
Около окружности радиуса r описана равнобокая трапеция с основаниями 2a и 2b?

Геометрия | 5 — 9 классы

Около окружности радиуса r описана равнобокая трапеция с основаниями 2a и 2b.

Докажите что r ^ 2 = ab.

Там у меня зачеркнуто, условие записал неверно, а потом увидел и исправил.

Там теорема Пифагора и теорема о сумместорон описанного четырехугольника.

Видео:Задача про трапецию, описанную около окружностиСкачать

Докажите что площадь прямоугольного трапеции описанной около окружности равен произведению оснований?

Докажите что площадь прямоугольного трапеции описанной около окружности равен произведению оснований.

Видео:Радиус описанной окружности трапецииСкачать

Помогите, пожалуйста?

С объяснением : ) Основания равнобокой трапеции равны 9 см и 21 см, а высота — 8 см.

Найдите радиус окружности, описанной около данной трапеции.

Видео:Геометрия Задача № 26 Найти радиус вписанной в трапецию окружностиСкачать

Основания равнобокой трапеции равны 9см и 21 см, а высота 8 см?

Основания равнобокой трапеции равны 9см и 21 см, а высота 8 см.

Найдите радиус окружности, описанной около данной трапеции?

Видео:Основания равнобедренной трапеции равны 72 и 30. Центр окружности, описанной около трапеции... (ЕГЭ)Скачать

Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная?

Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.

Видео:ТРАПЕЦИЯ — Что такое трапеция, Виды Трапеций, Площадь Трапеции // Геометрия 8 классСкачать

Около окружности описана равнобокая трапеция, длины оснований которой равны 3 и 6 ?

Около окружности описана равнобокая трапеция, длины оснований которой равны 3 и 6 .

Найти радиус окружности.

Видео:Боковые стороны трапеции, описанной около окружности, равны 13 и 1. Найдите среднюю линию трапеции.Скачать

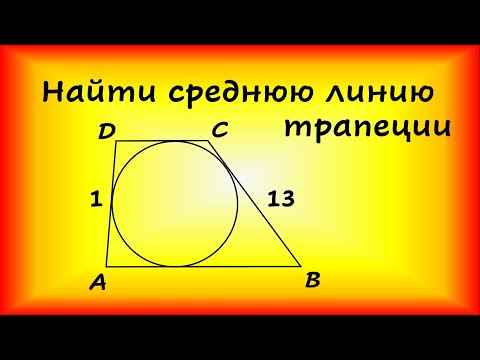
Трапеция с основаниями 9 и 16 см описана около окружности?

Трапеция с основаниями 9 и 16 см описана около окружности!

Найти радиус окружности.

Видео:В равнобедренной трапеции основания равны 2 и 8 ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

Равнобокая трапеция описана около окружности с радиусом 12дм?

Равнобокая трапеция описана около окружности с радиусом 12дм.

Точка касания делит ее боковую строну в отношении 9 : 4.

Найдите среднюю линию трапеции.

Видео:Трапеция. Задачи. Найти углы трапеции. Равнобедренной,прямоугольной,Скачать

Kak найти радиус описанной около трапеции окружности, если известно два основания?

Kak найти радиус описанной около трапеции окружности, если известно два основания?

Видео:Геометрия Равнобокая трапеция вписана в окружность, центр которой принадлежит одному из основанияСкачать

Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная?

Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.

Видео:Около трапеции описана окружностьСкачать

Основания трапеции равны 4 и 16?

Основания трапеции равны 4 и 16.

Найдите радиусы окружностей, вписанной в трапецию и описанной около неё, если известно, что эти окружности существуют.

На этой странице сайта размещен вопрос Около окружности радиуса r описана равнобокая трапеция с основаниями 2a и 2b? из категории Геометрия с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

Ответ : |BC| = a = 2√3. |2AO + 2CO| = 4. |AС — (3 / 2) * ОС| = 3. Объяснение : В равностороннем треугольнике центр описанной окружности лежит на пересечении высот треугольника, которые являются и биссектрисами и медианами. АО — радиус описанной о..

Привет, BD — выстота = >BDC = 90° найдем угол DBC = 180 — (90 + 42) = 48° Треугольники авd и abd равны = >ABD = 48 ABC = 48 + 48 = 96°.

Пусть A1 — начало координат Ось X — A1B Ось Y — A1D1 Ось Z — A1A A1D1 (0 ; 1 ; 0) M(1 ; 1 ; 0. 5) D(0 ; 1 ; 1) Уравнение A1MD ax + by + cz = 0 подставляем координаты точек a + b + 0. 5c = 0 b + c = 0 Пусть с = — 2 тогда b = 2 a = — 1 — x + 2y — 2z ..

Р = а + в + с (68 — 16) : 2 = 26(см) боковая сторона треугольника.

68 — 16 = 52приходится на две стороны, так как треугольник равнобедренный то стороны равные 52 : 2 = 26 боковая сторона.

36 : 2 = 18 — отрезок КВ 18 : 2 = 9 — отрезок МК.

1) Точки в пл. АДД1 : А , Д Д1 , А1 . Точки в пл. АВС : А , В , С , Д . 2) MS лежит в пл. АВСД МД в пл. АВСД и АА1Д1Д АВ в пл. АВСД и АА1В1В 3) АА1 , ВВ1 , СС1 , ДД1 перпендикулярны пл. АВСД 4) прямой АД параллельны пл. ВВ1С1С и А1В1С1Д1 5) ..

1)Угол 1 = 65, 2)180 — 65 = 115(угол 2) 3)180 — 115 = 65 градусов (угол 3) Эх, вернуться бы в 7 класс.

Пусть B начало координат Ось X — BA Ось Y — BC Ось Z — BB1 направляющий вектор BD (1 ; 0 ; 1) направляющий вектор DA1 (0 ; — 1 ; 1) Длина√2 | i j k | | 1 0 1| = i | 0 1| + j |1 1 | + k | 1 0 | | 0 — 1 1| | — 1 1| |0 1| | 0 — 1 | Длина√3 Расстояние√3 ..

В градусе 60 минут, значит 5°48′ + 7°35′ = 13°83′ = 14°23′ 32°17′ + 8°45′ = 40°62′ = 41°02′.

Видео:8 класс, 6 урок, ТрапецияСкачать

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Видео:ПЛАНИМЕТРИЯ ТРАПЕЦИЯ ВСЕ ДЛЯ ЧАЙНИКОВ НА ЕГЭ | ЗОТОТАЯ ЛИХОРАДКА 90-х| ГАРМАШУКСкачать

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Видео:Как найти стороны равнобокой трапеции, описанной около трёх попарно касающихся равных окружностей?Скачать

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Видео:Задание из ЕГЭ: трапеция в окружности #геометрия #егэ2023 #трапеция #окружностьСкачать

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Видео:Геометрия Площадь равнобедренной трапеции, описанной около круга, равна S, а высота трапеции в 2Скачать

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

🎦 Видео

Трапеция, решение задач. Вебинар | МатематикаСкачать

Задача.Высота трапеции, образованной касательными к двум окружностям.Скачать

Трапеция и вписанная окружностьСкачать