Вопрос по геометрии:
Расстояние между центрами двух окружностей,касающихся внешним образом,равно 18см.Найдите радиусы окружностей,если один из них в 2 раза больше другого.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
- Как написать хороший ответ?
- Две окружности на плоскости. Общие касательные к двум окружностям
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Как найти расстояние между центрами окружностей
- Взаимное расположение двух окружностей
- Формулы для длин общих касательных и общей хорды двух окружностей
- Доказательства формул для длин общих касательных и общей хорды двух окружностей
- Ответ
- Проверено экспертом
- 🎥 Видео
Ответы и объяснения 2
Обычное построение в таких задачах — проводится линия центров и центры соединяются с точками касания. Получается прямоугольная трапеция, в которой известна наклонная боковая сторона — это расстояние между центрами, равное 18.
Все это вобщем-то не нужно в решении, только проясняет суть.
Ясно, что R1 + R2 = 18, но R1 = 2*R2, поэтому R2 = 6, R1 = 12. Это всё :))
Поскольку эти окружности касаются в одной точке, их центры находися на одной прямой, проходящей через точку касания.
Примем меньший радиус за х. Тогда второй радиус равн 2х
х=6 см — меньший радиус
2х=12 см — большийрадиус.
Знаете ответ? Поделитесь им!
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
- Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
- Писать без грамматических, орфографических и пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
- Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
- Использовать мат — это неуважительно по отношению к пользователям;
- Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!
Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.
Видео:ОГЭ Задание 26 Внешнее касание двух окружностейСкачать

Две окружности на плоскости.
Общие касательные к двум окружностям
 Взаимное расположение двух окружностей Взаимное расположение двух окружностей |
 Общие касательные к двум окружностям Общие касательные к двум окружностям |
 Формулы для длин общих касательных и общей хорды Формулы для длин общих касательных и общей хорды |
 Доказательства формул для длин общих касательных и общей хорды Доказательства формул для длин общих касательных и общей хорды |
Видео:9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

Взаимное расположение двух окружностей
| Фигура | Рисунок | Свойства |
| Две окружности на плоскости |  | |
| Каждая из окружностей лежит вне другой |  | |
| Внешнее касание двух окружностей |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  |  |
| Каждая из окружностей лежит вне другой | ||
 | ||
| Внешнее касание двух окружностей | ||
 | ||
| Внутреннее касание двух окружностей | ||
 | ||
| Окружности пересекаются в двух точках | ||
 | ||
 | ||
| Каждая из окружностей лежит вне другой | ||
 Расстояние между центрами окружностей больше суммы их радиусов | ||
| Внешнее касание двух окружностей | ||
 Расстояние между центрами окружностей равно сумме их радиусов | ||
| Внутреннее касание двух окружностей | ||
| Окружности пересекаются в двух точках | ||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов r1 – r2 лежит внутри другой | ||
| Внутренняя касательная к двум окружностям |  | |
| Внутреннее касание двух окружностей |  | |
| Окружности пересекаются в двух точках |  | |
| Внешнее касание двух окружностей |  | |
 | ||
 | ||
| Внешняя касательная к двум окружностям | |
 | |
| Внутренняя касательная к двум окружностям | |
 | |
| Внутреннее касание двух окружностей | |
 | |
| Окружности пересекаются в двух точках | |
 | |
| Внешнее касание двух окружностей | |
 | |
 | |
| Каждая из окружностей лежит вне другой | |
 | |
| Внешняя касательная к двум окружностям | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутреннее касание двух окружностей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружности пересекаются в двух точках | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешнее касание двух окружностей | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Каждая из окружностей лежит вне другой | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фигура | Рисунок | Формула | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешняя касательная к двум окружностям |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Общая хорда двух пересекающихся окружностей |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешняя касательная к двум окружностям | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внутренняя касательная к двум окружностям | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Внешняя касательная к двум окружностям | |||||||||
| Внутренняя касательная к двум окружностям | |||||||||
| Общая хорда двух пересекающихся окружностей | |||||||||
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Две окружности | Резерв досрока ЕГЭ-2019. Задание 16. Профильный уровень | Борис Трушин |Скачать  Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Планиметрия 5 | mathus.ru | расстояние между центрами окружностей в параллелограммеСкачать  Как найти расстояние между центрами окружностейУ Вас недостаточно прав для добавления комментариев. Все права защищены 2019
Видео:Геометрия Две окружности радиусом R = 3 см и r = 1 см касаются внешним образом. Найти расстояние отСкачать  Взаимное расположение двух окружностей
Взаимное расположение на плоскости двух окружностей радиусов r1 и r2 с центрами O1 и O2 определяется расстоянием d между центрами этих окружностей | |||||||||
| Каждая из окружностей лежит вне другой |  | ||||||||
| Внешнее касание двух окружностей |  | ||||||||
| Внутреннее касание двух окружностей |  | ||||||||
| Окружности пересекаются в двух точках |  |  | |||||||
| Каждая из окружностей лежит вне другой | |||||||||
 | |||||||||
| Внешнее касание двух окружностей | |||||||||
 | |||||||||
| Внутреннее касание двух окружностей | |||||||||
 | |||||||||
| Окружности пересекаются в двух точках | |||||||||
 | |||||||||
 | |||||||||
| Каждая из окружностей лежит вне другой | |||||||||
 Расстояние между центрами окружностей больше суммы их радиусов | |||||||||
| Внешнее касание двух окружностей | |||||||||
 Расстояние между центрами окружностей равно сумме их радиусов | |||||||||
| Внутреннее касание двух окружностей | |||||||||
| Окружности пересекаются в двух точках | |||||||||
 Расстояние между центрами окружностей больше разности их радиусов, но меньше суммы их радиусов Расстояние между центрами окружностей меньше разности их радиусов d внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. | |||||||||
| Внутренняя касательная к двум окружностям |  | ||||||||
| Внутреннее касание двух окружностей |  | ||||||||
| Окружности пересекаются в двух точках |  | ||||||||
| Внешнее касание двух окружностей |  | ||||||||
 | |||||||||
 | |||||||||
| Внешняя касательная к двум окружностям | |
 | |
Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой.

Прямую называют внутренней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по разные стороны от этой прямой.

Существует единственная общая внешняя касательная. Других общих касательных нет.

Существуют две общих внешних касательных. Других общих касательных нет.

Существует единственная общая внутренняя касательная, а также две общих внешних касательных. Других общих касательных нет.

Существуют две общих внешних касательных, а также две общих внутренних касательных. Других общих касательных нет

| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Внутреннее касание двух окружностей |
| Окружности пересекаются в двух точках |
| Внешнее касание двух окружностей |
| Каждая из окружностей лежит вне другой |
| Фигура | Рисунок | Формула | ||
| Внешняя касательная к двум окружностям |  | |||
| Внутренняя касательная к двум окружностям |  | |||
| Общая хорда двух пересекающихся окружностей |  | |||
| Внешняя касательная к двум окружностям | |
 | |
Длина общей внешней касательной к двум окружностям вычисляется по формуле

Длина общей внутренней касательной к двум окружностям вычисляется по формуле

Длина общей хорды двух окружностей вычисляется по формуле
| Внешняя касательная к двум окружностям |
| Внутренняя касательная к двум окружностям |
| Общая хорда двух пересекающихся окружностей |
 Длина общей хорды двух окружностей вычисляется по формуле Видео:Три окружности касаются прямой и друг друга внешним образомСкачать 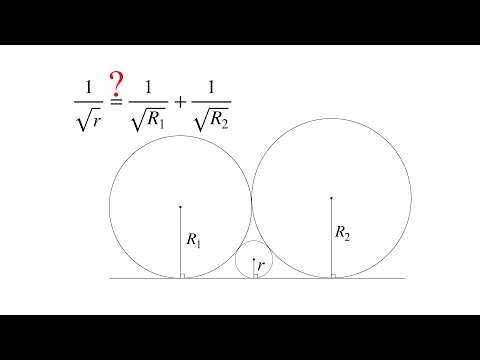 Доказательства формул для длин общих касательных и общей хорды двух окружностейУтверждение 1 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d (рис.1), то длина общей внешней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 2 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей внутренней касательной к этим окружностям вычисляется по формуле что и требовалось доказать. Утверждение 3 . Если расстояние между центрами двух окружностей радиусов r1 и r2 равно d , то длина общей хорды AB этих окружностей вычисляется по формуле Доказательство . Для того, чтобы найти длину общей хорды AB двух окружностей, введём, как показано на рисунке 3, Видео:Геометрия Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружСкачать  ОтветПроверено экспертомУравнение окружности с центром (a;b) и радиусом R центр окружности (-2;6) радиус 6 центр окружности (4;-5)радиус 5 по формуле расстояние между двумя точками : находим расстояние между центрами заданных окружностей 🎥 ВидеоОГЭ Задание 25 Внешнее касание двух окружностейСкачать  Параметр. Серия 13. Решение задач с окружностями. Касание двух окружностейСкачать  ОГЭ № 25. "Окружности касаются внешним образом... "Скачать  ЕГЭ и ОГЭ. Окружности и касательные, секущие, подобие. Свойства. Расстояние между центрами.Скачать  Занятие 1 к главе 9Скачать  Урок 47. Взаимное расположение окружностей (8 класс)Скачать  Касание окружностейСкачать  Взаимное расположение двух окружностей. Урок 8. Геометрия 9 классСкачать  Задание 26 Две окружности, внешнее касаниеСкачать  ЕГЭ задание 16 Внутреннее касание двух окружностейСкачать  ЕГЭ Задание 16 Комбинация трёх окружностейСкачать  |


























