Расстояние между параллельными прямыми а и б равно 7 см а расстояние между параллельными прямыми

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Этот видеоурок будет полезен тем, кто хочет самостоятельно изучить тему «Расстояние от точки до прямой. Расстояние между параллельными прямыми». В ходе урока вы сможете узнать о том, как можно рассчитать расстояние от точки до прямой. Затем учитель даст определение расстояния между параллельными прямыми.

Видео:19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Расстояние между параллельными прямыми — определение и вычисление с примерами решения

Содержание:

Расстояние от точки до прямой:

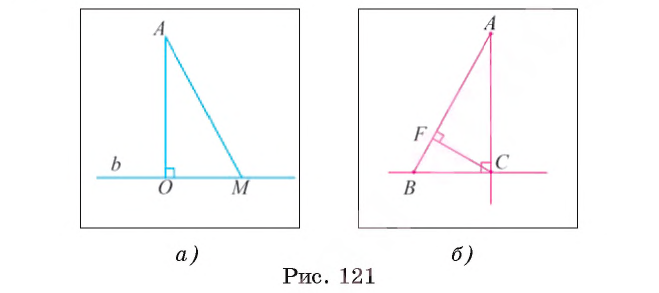
Введем теперь понятие расстояния от точки до прямой. Пусть точка А не лежит на прямой b и отрезок АО — перпендикуляр, проведенный из точки А к прямой b (рис. 121, a).

Наклонной к прямой b называется отрезок AM, где М — произвольная точка прямой b, не совпадающая с точкой О (см. рис. 121, а). В прямоугольном треугольнике АОМ катет АО меньше гипотенузы AM. Таким образом, перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к данной прямой.

Видео:7 класс, 38 урок, Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Определение расстояния от точки до прямой

Определение. Расстоянием от точки до прямой называется длина перпендикуляра, проведенного из этой точки к прямой.

Расстояние от точки А до прямой b обозначается d(A, b) (читают следующим образом: «Расстояние от точки А до прямой b»).

Например, если в прямоугольном треугольнике ABC угол С прямой, то расстояние от вершины А до прямой ВС равно длине катета АС, а расстояние от вершины В до прямой АС равно длине катета ВС (рис. 121, б). Длина отрезка CF, являющегося высотой этого треугольника, есть расстояние от вершины С до прямой АВ.

Воспользовавшись понятием расстояния от точки до прямой, можно определить понятие расстояния между параллельными прямыми.

Видео:№277. Расстояние между параллельными прямыми а и b равно 3 см, а между параллельными прямымиСкачать

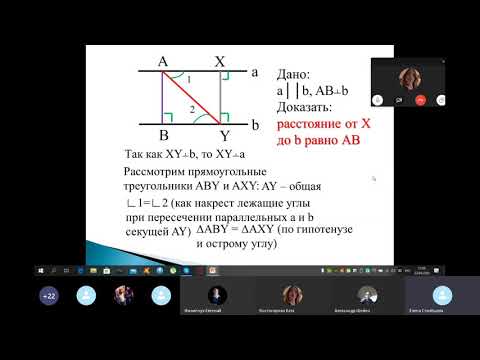
Расстояние между параллельными прямыми

Предварительно докажем еще одно свойство параллельных прямых.

Теорема. Все точки каждой из двух параллельных прямых находятся на равном расстоянии от другой прямой.

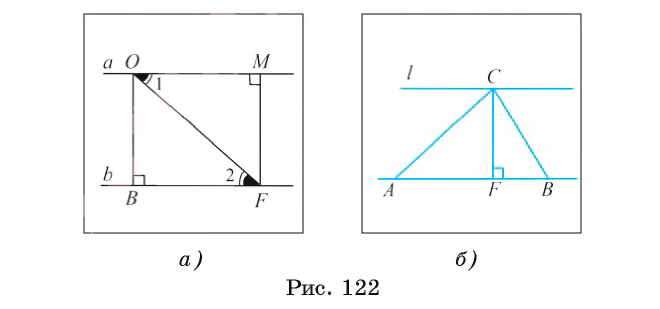
1) Пусть а и b две параллельные прямые, отрезок ОВ — перпендикуляр, проведенный из произвольной точки О прямой а к прямой b (рис. 122, а). Докажем, что расстояние от любой точки М прямой а до прямой b равно длине отрезка ОВ.

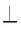
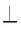
2) Проведем из точки М перпендикуляр MF к прямой b. Так как MF b, а прямые а и b параллельны, то MF а.

3) Прямоугольные треугольники OBF и OMF равны по гипотенузе и острому углу (сторона OF — общая, и равны внутренние накрест лежащие углы 1 и 2 при пересечении параллельных прямых а и b секущей OF). Из равенства треугольников следует, что MF = ОВ. Аналогично доказывается, что каждая точка прямой b находится на том же расстоянии от прямой а.

Определение. Расстоянием между двумя параллельными прямыми называется расстояние от произвольной точки одной из параллельных прямых до другой прямой.

Например, пусть прямая l проходит через вершину С треугольника ABC и параллельна его стороне АВ. Тогда расстояние между прямыми l и АВ равно длине отрезка CF, являющегося высотой треугольника ABC (рис. 122, б).

Правильная треугольная пирамида

Рассмотрим еще одну пространственную фигуру.

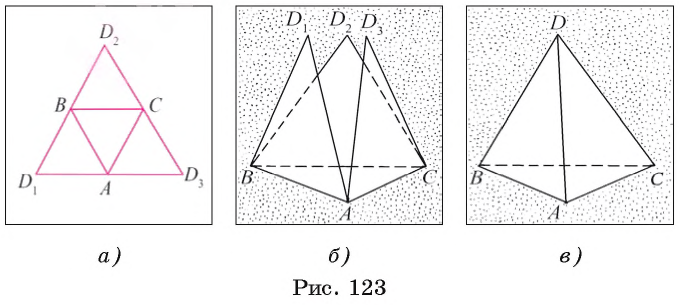
Проведем мысленный эксперимент. Представим, что часть листа бумаги, имеющая форму равностороннего треугольника, разбита на четыре части, каждая из которых имеет форму равностороннего треугольника (рис. 123, а). Такое разбиение осуществляют отрезки АВ, ВС и СА, которые соединяют середины сторон модели равностороннего треугольника.

Перегнем данную модель равностороннего треугольника по отрезкам АВ, ВС, СА и склеим так, чтобы вершины D₁, D₂ и D₃ совпали (рис. 123, б, в).

Фигура, состоящая из части пространства, ограниченной четырьмя равными равносторонними треугольниками DAB, DBC, DAC и ABC, и точек этих треугольников, называется тетраэдром (или правильным тетраэдром), который обозначается DABC (см. рис.123, в). Равносторонние треугольники DAB, DBC, DAC и ABC называются гранями тетраэдра, а их вершины и стороны — вершинами и ребрами тетраэдра.

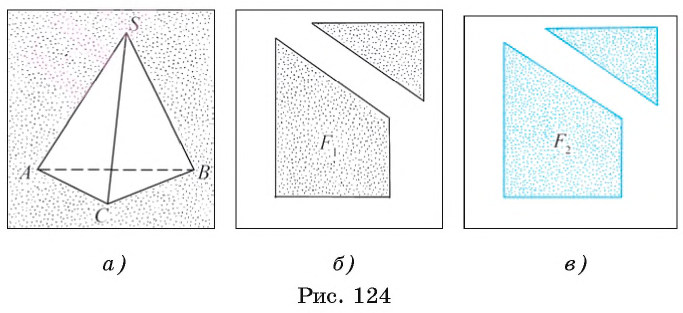
Правильная треугольная пирамида — это многогранник, у которого одна грань ABC — равносторонний треугольник, а остальные три грани — равные равнобедренные треугольники SAB, SBC, SAC, имеющие общую вершину S (рис. 124, а). Равносторонний треугольник ABC называется основанием правильной треугольной пирамиды, а треугольники SAB, SBC, SAC — ее боковыми гранями. Общая вершина S треугольников SAB, SBC, SAC называется вершиной пирамиды, стороны SA, SB, SC — боковыми ребрами правильной треугольной пирамиды, а вершины А, В, С называются вершинами при основании пирамиды.

Треугольная пирамида, основанием которой служит равносторонний треугольник ABC, а вершиной — точка S, обозначается SABC.

Так как равносторонний треугольник является равнобедренным, то понятно, что любой тетраэдр служит примером правильной треугольной пирамиды.

Равенство фигур

Ранее мы изучили понятия равенства отрезков, углов и треугольников. Треугольники называются равными, если они совмещаются при наложении. Аналогично определяется и равенство произвольных геометрических фигур.

Представление о моделях двух равных прямоугольников дают, например, два одинаковых листа писчей бумаги или два листа одной и той же книги. Модели равных фигур более сложной формы получим, если от одинаковых листов бумаги прямоугольной формы отрежем части, имеющие форму равных прямоугольных треугольников, как показано на рисунке 124, б, в.

Легко проверить, что части F₁ и F₂, оставшиеся после отрезания, можно совместить наложением, что служит подтверждением их одинаковой формы и размеров.

Как и в случае треугольников, можно говорить о равенстве двух произвольных фигур в случае их совмещения при наложении.

Две геометрические фигуры называются равными, если их можно совместить наложением.

В общем случае при рассмотрении равных фигур пользуются следующими свойствами равных фигур:

1. любая фигура равна самой себе;
2. если фигура F₁ равна фигуре F₂, то фигура F₂ равна фигуре F₁;
3. если фигура F₁ равна фигуре F₂, а фигура F₂ равна фигуре F₃, то фигура F₁ равна фигуре F₃.

В предыдущих главах были изучены признаки равенства треугольников, расположенных в одной и той же плоскости. Заметим, что эти признаки справедливы и для треугольников, которые лежат в разных плоскостях.

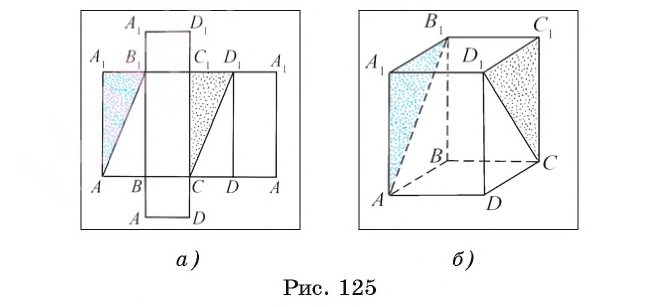
Рассмотрим некоторые примеры. Пусть у нас есть развертка прямоугольного параллелепипеда, основаниями которого служат квадраты (рис. 125, а). На рисунке одинаковыми буквами обозначены точки, которые «склеиваются» в одну вершину параллелепипеда. Нетрудно понять, что отмеченные на развертке прямоугольные треугольники равны по двум катетам, а соответствующие им равные прямоугольные треугольники АА₁В₁ и D₁C₁C лежат в разных гранях прямоугольного параллелепипеда, а значит, — в разных плоскостях (рис. 125, б).

В дальнейшем при решении некоторых задач мы будем пользоваться утверждением о том, что признаки равенства треугольников справедливы и для треугольников, расположенных в разных плоскостях.

Пример №1

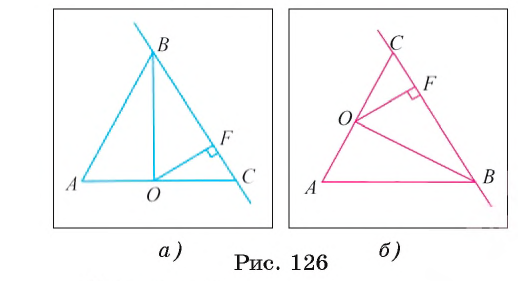
Точка О — середина стороны А С равностороннего треугольника ABC. Вычислите расстояние от точки О до прямой ВС, если ВО = 8 см (рис. 126, а, б).

АВС,

О АС,

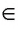
Расстояние от точки О до прямой ВС равно длине перпендикуляра, проведенного из точки О к прямой ВС.

1) Пусть OF — перпендикуляр, проведенный из точки О к прямой ВС, тогда d(O, ВС) равно длине отрезка OF, который является катетом прямоугольного треугольника BFO.

2) Так как треугольник ABC равносторонний, а значит, и равнобедренный (АВ = ВС), то его медиана ВО является биссектрисой. Так как градусная мера каждого угла равностороннего треугольника равна 60°, то OBC = ABC = 30°.

3) В прямоугольном треугольнике BFO ( OFB = 90°) катет OF лежит против угла в 30°, следовательно, OF = В0 = 4 см, т. е. d(O, ВС) = 4 см.

Пример №2

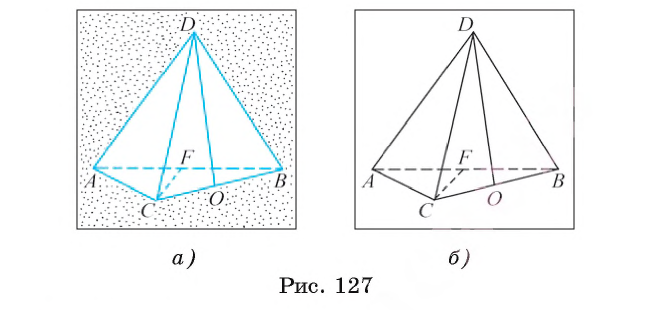
Точки О и F — соответственно середины ребер В С и АВ тетраэдра DABC. Докажите, что DO = CF (рис. 127, а, б).

Для д оказательства равенства отрезков достаточно доказать равенство треугольников, сторонами которых являются эти отрезки. В данном случае можем рассмотреть треугольники AFC и BOD.

1) Так как точки О и F — середины сторон СВ и АВ равносторонних треугольников CBD и АСВ соответственно, то медианы DO и CF этих треугольников являются также и высотами. Следовательно, треугольники BOD и AFC являются прямоугольными.

2) Поскольку треугольники CBD и АСВ — равные и равносторонние, то АС = BD и CAB = DBC = 60°.

3) Таким образом, прямоугольные треугольники BOD и AFC равны по гипотенузе и острому углу (AC = DB, FAC = OBD = 60°). Из равенства этих треугольников следует, что DO = CF, что и требовалось доказать.

• Задачи на построение циркулем и линейкой
• Задачи на построение по геометрии
• Угол — определение, виды, как обозначают с примерами
• Перпендикулярные прямые в геометрии
• Параллельные прямые
• Соотношения между сторонами и углами треугольника
• Неравенство треугольника — определение и вычисление
• Свойства прямоугольного треугольника

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Геометрия 7 класс (Урок№26 - Расстояние от точки до прямой. Расстояние между параллельными прямыми.)Скачать

Расстояние между двумя параллельными прямыми: определение и примеры нахождения

В материале этой статьи разберем вопрос нахождения расстояния между двумя параллельными прямыми, в частности, при помощи метода координат. Разбор типовых примеров поможет закрепить полученные теоретические знания.

Видео:Определение расстояние между параллельными прямыми (Способ замены плоскостей проекции).Скачать

Расстояние между двумя параллельными прямыми: определение

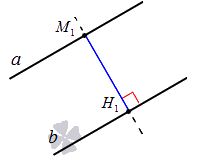
Расстояние между двумя параллельными прямыми – это расстояние от некоторой произвольной точки одной из параллельных прямых до другой прямой.

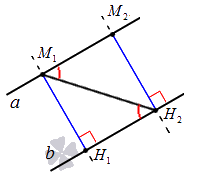
Приведем иллюстрацию для наглядности:

На чертеже изображены две параллельные прямые a и b . Точка М 1 принадлежит прямой a , из нее опущен перпендикуляр на прямую b . Полученный отрезок М 1 Н 1 и есть расстояние между двумя параллельными прямыми a и b .

Указанное определение расстояния между двумя параллельными прямыми справедливо как на плоскости, так и для прямых в трехмерном пространстве. Кроме того, данное определение взаимосвязано со следующей теоремой.

Когда две прямые параллельны, все точки одной из них равноудалены от другой прямой.

Пусть нам заданы две параллельные прямые a и b . Зададим на прямой а точки М 1 и М 2 , опустим из них перпендикуляры на прямую b , обозначив их основания соответственно как Н 1 и Н 2 . М 1 Н 1 – это расстояние между двумя параллельными прямыми по определению, и нам необходимо доказать, что | М 1 Н 1 | = | М 2 Н 2 | .

Пусть будет также существовать некоторая секущая, которая пересекает две заданные параллельные прямые. Условие параллельности прямых, рассмотренное в соответствующей статье, дает нам право утверждать, что в данном случае внутренние накрест лежащие углы, образованные при пересечении секущей заданных прямых, являются равными: ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Прямая М 2 Н 2 перпендикулярна прямой b по построению, и, конечно, перпендикулярна прямой a . Получившиеся треугольники М 1 Н 1 Н 2 и М 2 М 1 Н 2 являются прямоугольными и равными друг другу по гипотенузе и острому углу: М 1 Н 2 – общая гипотенуза, ∠ M 2 M 1 H 2 = ∠ H 1 H 2 M 1 . Опираясь на равенство треугольников, мы можем говорить о равенстве их сторон, т.е.: | М 1 Н 1 | = | М 2 Н 2 | . Теорема доказана.

Отметим, что расстояние между двумя параллельными прямыми – наименьшее из расстояний от точек одной прямой до точек другой.

Видео:Расстояние от точки до прямой. Расстояние между параллельными прямыми, 7 классСкачать

Нахождение расстояния между параллельными прямыми

Мы уже выяснили, что, по сути, чтобы найти расстояние между двумя параллельными прямыми, необходимо определить длину перпендикуляра, опущенного из некой точки одной прямой на другую. Способов, как это сделать, несколько. В каких-то задачах удобно воспользоваться теоремой Пифагора; другие предполагают использование признаков равенства или подобия треугольников и т.п. В случаях, когда прямые заданы в прямоугольной системе координат, возможно вычислить расстояние между двумя параллельными прямыми, используя метод координат. Рассмотрим его подробнее.

Зададим условия. Допустим, зафиксирована прямоугольная система координат, в которой заданы две параллельные прямые a и b . Необходимо определить расстояние между заданными прямыми.

Решение задачи построим на определении расстояния между параллельными прямыми: для нахождения расстояния между двумя заданными параллельными прямыми необходимо:

— найти координаты некоторой точки М 1 , принадлежащей одной из заданных прямых;

— произвести вычисление расстояния от точки М 1 до заданной прямой, которой эта точка не принадлежит.

Опираясь на навыки работы с уравнениями прямой на плоскости или в пространстве, определить координаты точки М 1 просто. При нахождении расстояния от точки М 1 до прямой пригодится материал статьи о нахождении расстояния от точки до прямой.

Вернемся к примеру. Пусть прямая a описывается общим уравнением A x + B y + C 1 = 0 , а прямая b – уравнением A x + B y + C 2 = 0 . Тогда расстояние между двумя заданными параллельными прямыми возможно вычислить, используя формулу:

M 1 H 1 = C 2 — C 1 A 2 + B 2

Выведем эту формулу.

Используем некоторую точку М 1 ( x 1 , y 1 ) , принадлежащую прямой a . В таком случае координаты точки М 1 будут удовлетворять уравнению A x 1 + B y 1 + C 1 = 0 . Таким образом, справедливым является равенство: A x 1 + B y 1 + C 1 = 0 ; из него получим: A x 1 + B y 1 = — C 1 .

Когда С 2 0 , нормальное уравнение прямой b будет иметь вид:

A A 2 + B 2 x + B A 2 + B 2 y + C 2 A 2 + B 2 = 0

При С 2 ≥ 0 нормальное уравнение прямой b будет выглядеть так:

A A 2 + B 2 x + B A 2 + B 2 y — C 2 A 2 + B 2 = 0

И тогда для случаев, когда С 2 0 , применима формула: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2 .

А для С 2 ≥ 0 искомое расстояние определяется по формуле M 1 H 1 = — A A 2 + B 2 x 1 — B A 2 + B 2 y 1 — C 2 A 2 + B 2 = = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2

Таким образом, при любом значении числа С 2 длина отрезка | М 1 Н 1 | (от точки М 1 до прямой b ) вычисляется по формуле: M 1 H 1 = A A 2 + B 2 x 1 + B A 2 + B 2 y 1 + C 2 A 2 + B 2

Выше мы получили: A x 1 + B y 1 = — C 1 , тогда можем преобразовать формулу: M 1 H 1 = — C 1 A 2 + B 2 + C 2 A 2 + B 2 = C 2 — C 1 A 2 + B 2 . Так мы, собственно, получили формулу, указанную в алгоритме метода координат.

Разберем теорию на примерах.

Заданы две параллельные прямые y = 2 3 x — 1 и x = 4 + 3 · λ y = — 5 + 2 · λ . Необходимо определить расстояние между ними.

Решение

Исходные параметрические уравнения дают возможность задать координаты точки, через которую проходит прямая, описываемая параметрическими уравнениями. Таким образом, получаем точку М 1 ( 4 , — 5 ) . Требуемое расстояние – это расстояние между точкой М 1 ( 4 , — 5 ) до прямой y = 2 3 x — 1 , произведем его вычисление.

Заданное уравнение прямой с угловым коэффициентом y = 2 3 x — 1 преобразуем в нормальное уравнение прямой. С этой целью сначала осуществим переход к общему уравнению прямой:

y = 2 3 x — 1 ⇔ 2 3 x — y — 1 = 0 ⇔ 2 x — 3 y — 3 = 0

Вычислим нормирующий множитель: 1 2 2 + ( — 3 ) 2 = 1 13 . Умножим на него обе части последнего уравнения и, наконец, получим возможность записать нормальное уравнение прямой: 1 13 · 2 x — 3 y — 3 = 1 13 · 0 ⇔ 2 13 x — 3 13 y — 3 13 = 0 .

При x = 4 , а y = — 5 вычислим искомое расстояние как модуль значения крайнего равенства:

2 13 · 4 — 3 13 · — 5 — 3 13 = 20 13

Ответ: 20 13 .

В фиксированной прямоугольной системе координат O x y заданы две параллельные прямые, определяемые уравнениями x — 3 = 0 и x + 5 0 = y — 1 1 . Необходимо найти расстояние между заданными параллельными прямыми.

Решение

Условиями задачи определено одно общее уравнение, задаваемое одну из исходных прямых: x-3=0. Преобразуем исходное каноническое уравнение в общее: x + 5 0 = y — 1 1 ⇔ x + 5 = 0 . При переменной x коэффициенты в обоих уравнениях равны (также равны и при y – нулю), а потому имеем возможность применить формулу для нахождения расстояния между параллельными прямыми:

M 1 H 1 = C 2 — C 1 A 2 + B 2 = 5 — ( — 3 ) 1 2 + 0 2 = 8

Ответ: 8 .

Напоследок рассмотрим задачу на нахождение расстояния между двумя параллельными прямыми в трехмерном пространстве.

В прямоугольной системе координат O x y z заданы две параллельные прямые, описываемые каноническими уравнениями прямой в пространстве: x — 3 1 = y — 1 = z + 2 4 и x + 5 1 = y — 1 — 1 = z — 2 4 . Необходимо найти расстояние между этими прямыми.

Решение

Из уравнения x — 3 1 = y — 1 = z + 2 4 легко определются координаты точки, через которую проходит прямая, описываемая этим уравнением: М 1 ( 3 , 0 , — 2 ) . Произведем вычисление расстояния | М 1 Н 1 | от точки М 1 до прямой x + 5 1 = y — 1 — 1 = z — 2 4 .

Прямая x + 5 1 = y — 1 — 1 = z — 2 4 проходит через точку М 2 ( — 5 , 1 , 2 ) . Запишем направляющий вектор прямой x + 5 1 = y — 1 — 1 = z — 2 4 как b → с координатами ( 1 , — 1 , 4 ) . Определим координаты вектора M 2 M → :

M 2 M 1 → = 3 — ( — 5 , 0 — 1 , — 2 — 2 ) ⇔ M 2 M 1 → = 8 , — 1 , — 4

Вычислим векторное произведение векторов :

b → × M 2 M 1 → = i → j → k → 1 — 1 4 8 — 1 — 4 = 8 · i → + 36 · j → + 7 · k → ⇒ b → × M 2 M 1 → = ( 8 , 36 , 7 )

Применим формулу расчета расстояния от точки до прямой в пространстве:

M 1 H 1 = b → × M 2 M 1 → b → = 8 2 + 36 2 + 7 2 1 2 + ( — 1 ) 2 + 4 2 = 1409 3 2

📸 Видео

Расстояние между параллельными прямымиСкачать

Параллельные прямые | Математика | TutorOnlineСкачать

Урок 23. Расстояние между параллельными прямыми (7 класс)Скачать

38. Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

Геометрия. 7 класс. Расстояние от точки до прямой. Расстояние между параллельными прямыми.Скачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать

Геометрия. Свойства параллельных прямых. Расстояние между параллельными прямымиСкачать

Расстояние от точки до прямой. Расстояние между параллельными прямымиСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

7 класс "Расстояние от точки до прямой.Расстояние между параллельными прямыми" учитель Радченко Е.В.Скачать

Расстояние от точки до прямой. Расстояние между параллельными прямыми.Скачать

Расстояние между скрещивающимися прямыми за 1 минуту. #математикапрофиль2023 #егэ2023 #школа #fypСкачать

Расстояние между параллельными и скрещивающимися прямыми | МатематикаСкачать

Видеоурок "Расстояние между прямыми в пространстве"Скачать