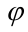Построить линию пересечения плоскостей определить видимость плоскостей с окружностью

Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.

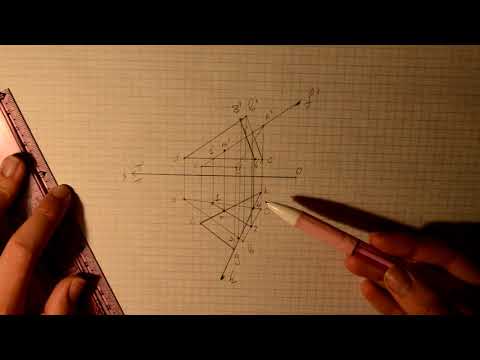
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L₁ и L₂, принадлежащих линии пересечения.

1. Вводим вспомогательную горизонтальную плоскость γ₁. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1»C» и 2»3», совпадают с фронтальным следом пл. γ₁. Он обозначен на рисунке как f_0γ1 и расположен параллельно оси x.
2. Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
3. Находим горизонтальную проекцию точки L₁ на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L₁ лежит на фронтальном следе плоскости γ.
4. Вводим вспомогательную горизонтальную плоскость γ₂. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L₂.
5. Через L₁ и L₂ проводим искомую прямую l.

Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.

Видео:Пересечение двух плоскостей. Плоскости в виде треугольникаСкачать

Пересечение плоскостей, заданных следами

Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П₁ и П₂.

1. Находим точку L’₁, расположенную на пересечении горизонтальных следов h_0α и h_0β. Точка L»₁ лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’₁.
2. Находим точку L»₂ на пересечении фронтальных следов пл. α и β. Точка L’₂ лежит на оси x. Её положение определяется по линии связи, проведенной из L»₂.
3. Проводим прямые l’ и l» через соответствующие проекции точек L₁ и L₂, как это показано на рисунке.

Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.

Видео:Построить линию пересечения треугольников ABC и DEF. Определить видимость. Вариант 2Скачать

Пересечение плоскостей треугольников

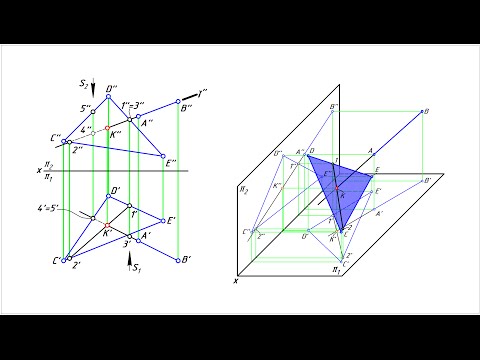
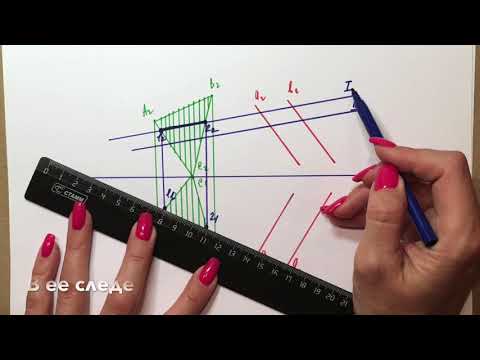
Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

1. Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f_0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3»=A»B»∩f_0σ и 5»=A»С»∩f_0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
2. Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N» расположена на фронтальном следе f_0σ на одной линии связи с N’.

Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f_0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.

Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₂. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π₂. С противоположной стороны от линии N»K» видимость треугольников меняется.

Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₁. Так как (∙)6» находится выше, чем (∙)7», то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π₁. С противоположной стороны от линии N’K’ видимость треугольников меняется.

Видео:Линия пересечения плоскостейСкачать

Построение линии пересечения поверхностей с примерами

Содержание:

Построение линии пересечения поверхностей:

Предложенные задания охватывают задачи не на все методы построения линий пересечения поверхностей, а только наиболее распространенные. Ниже приведены решения типовых задач, когда применены различные способы в зависимости от формы и расположения пересекающихся поверхностей.

Видео:Точка встречи прямой с плоскостьюСкачать

Одна из поверхностей занимает частное (проецирующее) положение

Задание: даны две поверхности:

Решение: поверхность цилиндра перпендикулярна к

Ниже приводится построение горизонтальной проекции только одной точки 1 (рис. 13.1). Из этой точки вниз проводят линию проекционной связи. Одновременно из этой же точки радиусом проводят дугу окружности, на которой лежит эта точка, как принадлежащая тору, и находят проекцию этой окружности на горизонтальной проекции тора — это прямая линия, параллельная оси x. Она проходит через точку (точка пересечения окружности, проходящей через точку 1, с окружностью тора, лежащей на ). Горизонтальная проекция точки 1 находится на пересечении линии проекционной связи, проведенной из точки , с горизонтальной проекцией окружности тора, на которой лежит точка 1. Остальные точки строят аналогично точке 1 (рис. 13.2).

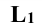
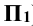
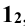
Точки 4 и 9 определяют видимость линии пересечения на горизонтальной проекции, а точки 1 и 2 наиболее удаленные от контура на горизонтальной проекции. Эту задачу можно решать и методом вспомогательных секущих плоскостей, который рассматривается далее.

Видео:Пересечение прямой с плоскостью общего положения. Определение видимости методом конкурирующих точекСкачать

Метод вспомогательных секущих плоскостей

Этот метод применяется для построения линии пересечения двух поверхностей, когда секущие (параллельные) плоскости при пересечении с данными поверхностями образуют простые для построения линии (прямую или окружность).

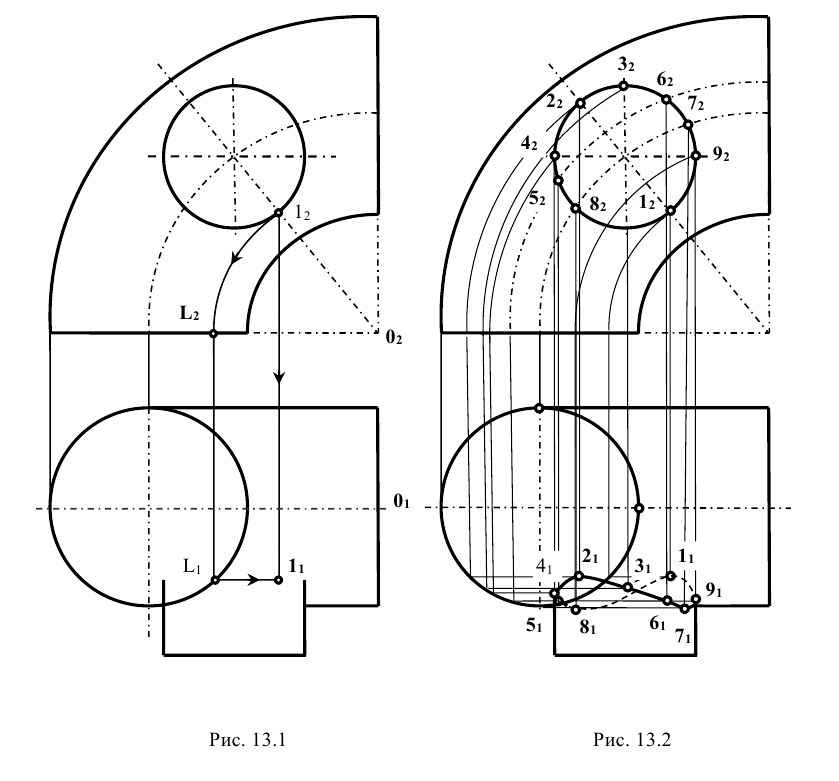
Задание: даны поверхности конуса 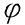и цилиндра Ф (рис. 13.3). Требуется построить линию их пересечения.

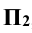
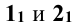
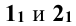
Решение: ось цилиндра перпендикулярна к плоскости , следовательно, поверхность цилиндра — проецирующая. В этом случае задача может быть решена так, как это было разобрано в предыдущем (п. 13.1.1) примере. Для этого определяют характерные -наивысшую и низшую точки линии пересечения 1 и 2, лежащие на пересечении фронтальной проекции цилиндра с очерковой образующей конуса. Их горизонтальные проекции принадлежат горизонтальной проекции очерковой образующей конуса (, совпадают с осевой линией конуса). Точки 3 и 4 определяют видимость линий пересечения на горизонтальной проекции.

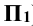
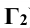
Для определения их горизонтальных проекций через ось цилиндра параллельно проводят вспомогательную секущую плоскость Г (ее фронтальный след ).

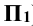
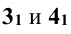
Эта плоскость рассечет цилиндр по очерковым образующим, а конус по окружности радиуса R, которая на будет проецироваться в натуральную величину. Пересечение этой окружности с очерковыми образующими цилиндра есть не что иное, как горизонтальные проекции характерных точек (рис. 13.3).

Построение промежуточных точек аналогично построению точек 3 и 4, только образующие, по которым вспомогательная плоскость будет рассекать цилиндр, не будут очерковыми (рис. 13.4).

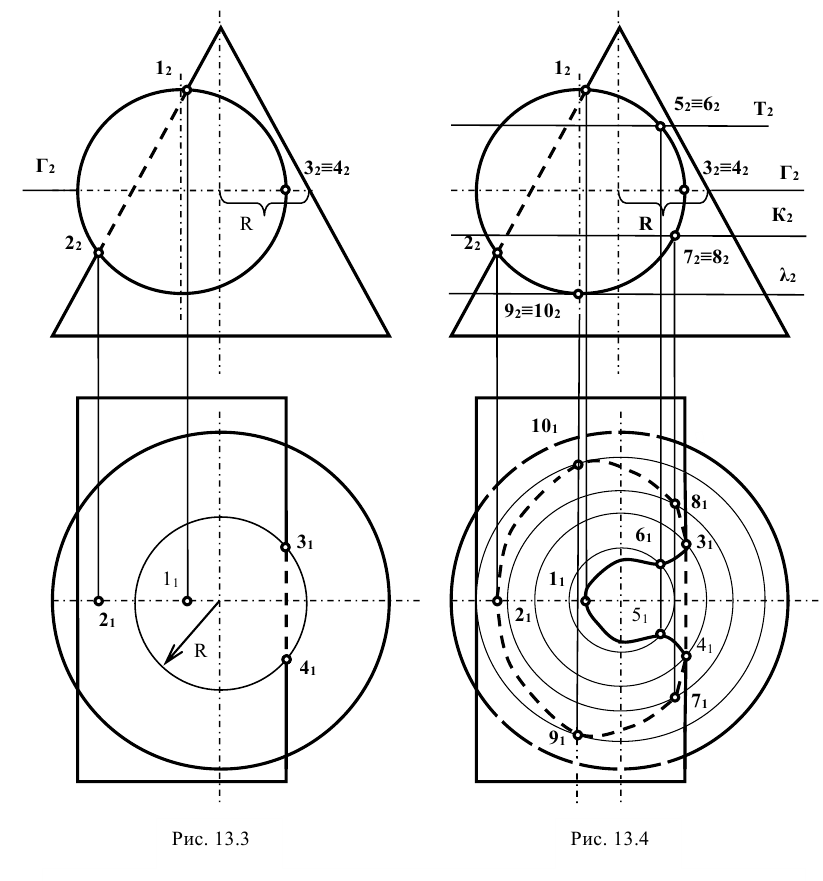
Задание: Даны две поверхности вращения — конус и цилиндр, оси которых пересекаются и находятся в одной плоскости, параллельной 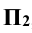(рис. 13.5). Требуется построить линию их пересечения.

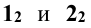
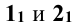
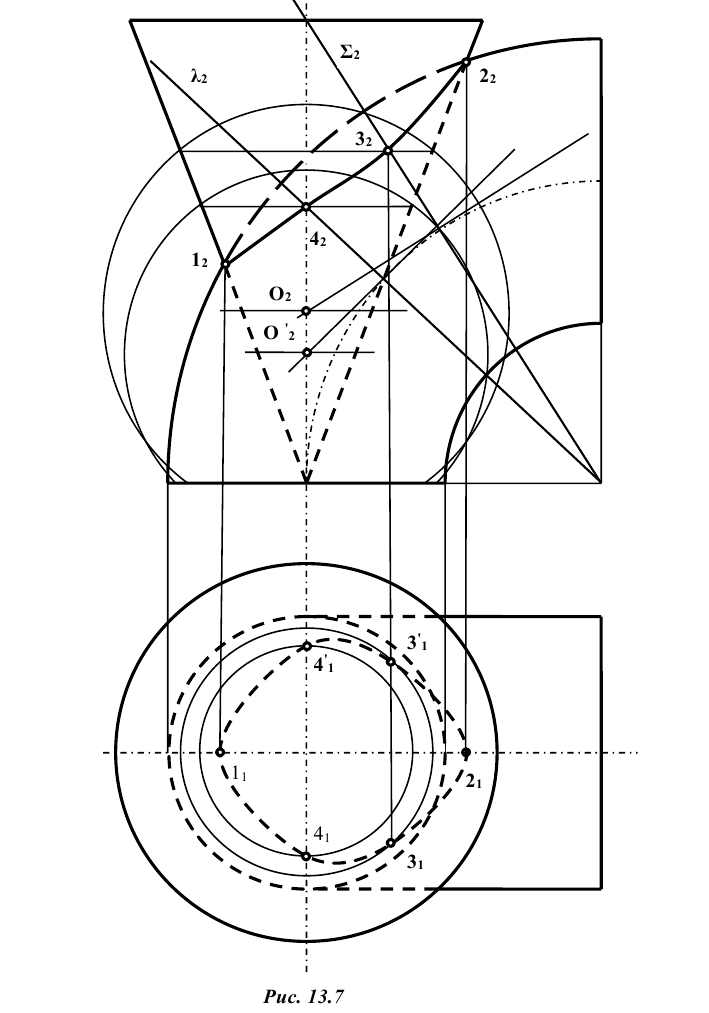
Решение: на фронтальной проекции фиксируют точки пересечения заданных поверхностей вращения — они принадлежат искомой линии пересечения. Горизонтальные проекции этих точек находятся на осевой линии конуса и цилиндра – .

Другие точки линии пересечения можно построить, используя концентрические сферические поверхности. Из точки пересечения осей фронтальных проекций, как из центра, проводятся сферы. Первая — касательная к проекции конуса, а последующие — большим радиусом (рис. 13.6). Каждая сфера пересекает обе поверхности по окружностям, фронтальные проекции которых изображаются отрезками прямых линий. Эти проекции пересекаются в точках, являющихся фронтальными проекциями точек искомой линии пересечения поверхностей.

Горизонтальные проекции этих точек определяются по принадлежности одной из поверхностей. В данном случае удобнее их получать по принадлежности конусу. Например, точки 3 и 4 лежат на той же окружности, по которой вспомогательная сфера пересекает конус. Изменяя радиус вспомогательной секущей сферы, находят ряд точек линии пересечения, соединив которые, получают проекции искомой линии (рис. 13.6). Чтобы определить видимость горизонтальной проекции линии пересечения, на её фронтальной проекции отмечают точки, лежащие на проекции осевой линии цилиндра и принадлежащие линии пересечения.

Затем по линиям проекционной связи переносят их на очерковые образующие горизонтальной проекции цилиндра. Точки, лежащие ниже указанных, будут находиться на невидимой части цилиндра.

Видео:Взаимное пересечение двух плоскостейСкачать

Метод эксцентрических сфер

Метод эксцентрических сфер применяется для построения линии пересечении поверхностей вращения, у которых оси расположены в одной плоскости, являющейся плоскостью симметрии. При этом пересекающиеся поверхности должны иметь семейство круговых сечений.

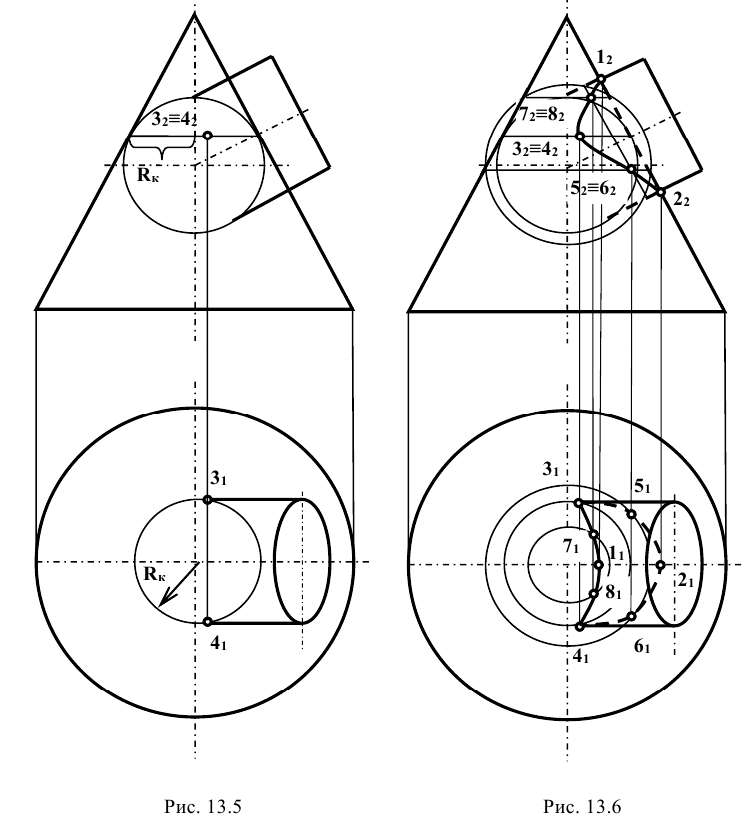
Задание: даны две поверхности вращения — тор и конус, оси которых находятся в одной плоскости, параллельной 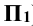(рис. 13.7). Требуется построить линии их пересечения.

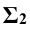
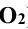
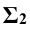
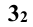
Решение: прежде всего, фиксируют опорные точки пересечения очерковых меридианов 1 и 2. Затем через ось вращения поверхности кольца проводят фронтальный след фронтально проецирующей плоскости Σ. Линия пересечения её с поверхностью тора — окружность. Центр сферы, пересекающей кольцо по окружности, находится на перпендикуляре, восстановленном из центра такой окружности к секущей проецирующей плоскости. Чтобы конус пересекался вспомогательной секущей сферой по окружности, её центр должен находиться на оси конуса. Точка пересечения перпендикуляра к проецирующей плоскости с осью конуса () выбирается центром вспомогательной секущей сферы. Радиус ее равен расстоянию от центра до точки пересечения меридиана тора со следом плоскости . Такая вспомогательная секущая сфера пересекает кольцо и конус вращения по окружностям, фронтальные проекции которых — проекции прямых. Точка пресечения этих отрезков (рис. 13.7) принадлежит искомой линии пересечения поверхностей.

Вспомогательные сферы имеют различные центры на оси конуса вращения; так, при построении проекции — точки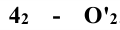. Горизонтальные проекции точек пересечения строят по принадлежности этих точек к одной из поверхностей, используя параллели, например, конуса.

Видео:Нахождение линии пересечения плоскостей путём приглашения плоскостей посредниковСкачать

Пересечение линии с поверхностью

В общем случае для графического определения положения точек пересечения линии с поверхностью необходимо выполнить ряд геометрических построений в следующей последовательности: заключить линию во вспомогательную поверхность; определить линию пересечения этой поверхности с заданной поверхностью; отметить точки пересечения построенной линии с заданной.

Этот алгоритм является универсальным, пригодным для решения любых задач. Ранее (лекция 4, рис. 4.5 и 4.6) он применялся для построения проекций точки пересечения прямой с плоскостью, где в качестве вспомогательной секущей поверхности использовалась плоскость и строилась прямая линии пересечения ее с заданной плоскостью, а искомая проекция точки пересечения определялась как место пересечения этой линии с заданной прямой.

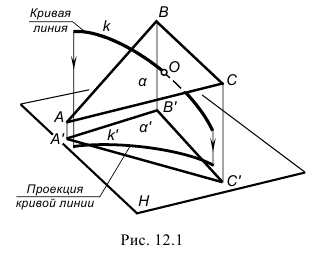
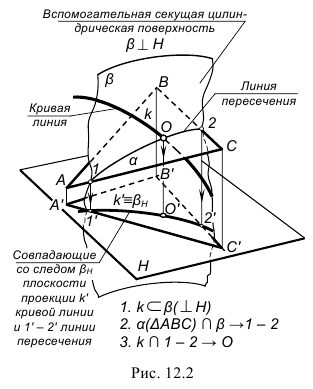
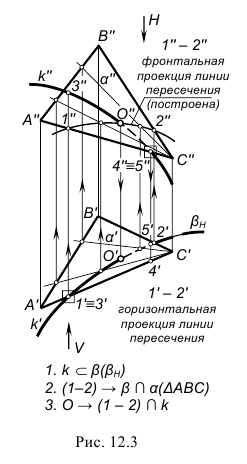
На рис. 12.1–12.3 проиллюстрирован тот же алгоритм применительно к построению точки пересечения кривой линии k с плоскостью α(∆ABC).

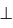
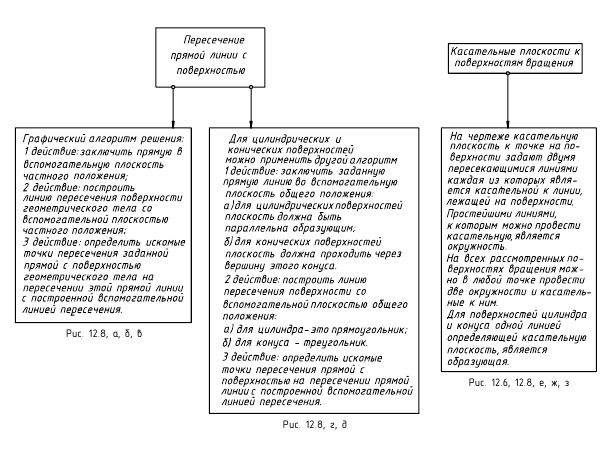
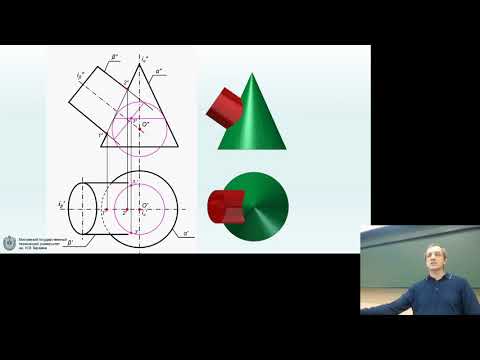
В качестве секущей поверхности в данном случае следует использовать проецирующую цилиндрическую поверхность, в частности, горизонтально-проецирующую β(β_H)H, в которую должна быть заключена кривая k(k»,k’). Для этого на чертеже (рис. 12.3) обозначаем горизонтальный след этой поверхности β_H. Горизонтальная проекция линии ее пересечения с заданной плоскостью α(∆ABC) совпадает с ним, располагаясь между точками 1′-2′. Для построения ее фронтальной проекции воспользуемся произвольными вспомогательными прямыми линиями, принадлежащими плоскости. Вначале задаем их горизонтальные проекции, например, через вершину C. Затем по точкам их пересечения со стороной AB находим фронтальные проекции вспомогательных прямых и определяем на них фронтальные проекции точек пересечения с ними заданной кривой. Проводим через найденные точки плавную кривую линию, являющуюся, таким образом, фронтальной проекцией линии пересечения, и отмечаем на ней место пересечения с фронтальной проекцией заданной кривой k(k»,k’) – точку O». Это и будет фронтальная проекция искомой точки пересечения заданной кривой k(k»,k’) с плоскостью α(∆ABC). Затем, воспользовавшись линией связи, находим горизонтальную проекцию O’ точки пересечения.

Этот алгоритм применен и для построения точек пересечения прямой линии с поверхностями геометрических тел – призмы, пирамиды и самопересекающегося тора (рис. 12.8, а, б, в). Поскольку поверхности этих тел являются замкнутыми, то необходимо найти по две точки пересечения на каждой из них.

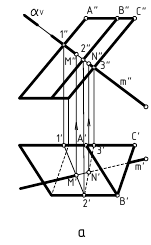
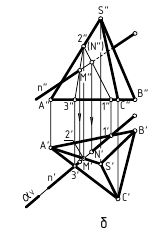
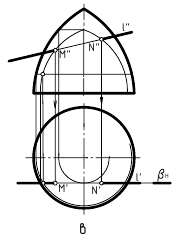
При пересечении с призмой (рис. 12.8, а) в качестве секущей плоскости для заключения в нее заданной прямой m(m»,m’) использовалась фронтально-проецирующая плоскость α_V. При пересечении с пирамидой (рис. 12.8, б) в качестве секущей плоскости для заключения в нее заданной прямой n(n»,n’) использовалась горизонтально-проецирующая плоскость α_H. При пересечении с самопересекающимся тором (рис. 12.8, в) в качестве секущей плоскости для заключения в нее заданной прямой l(l»,l’) использовалась фронтальная плоскость β_H. Далее все действия аналогичны рассмотренным. В каждом случае вначале строилась линия пересечения поверхности плоскостью, исходя из ее проецирующего положения, определялись на ней точки пересечения с заданной прямой, а при окончательном оформлении – видимость на чертеже.

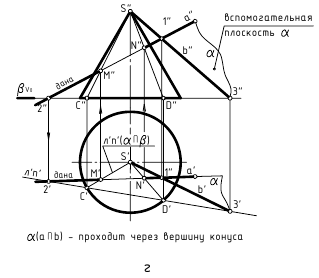
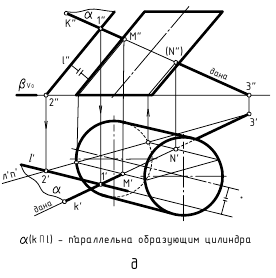
В качестве секущей плоскости при определении точек пересечения прямой с поверхностью могут использоваться также плоскости общего положения, пересекающие поверхность вдоль ее образующих (рис. 12.8, г, д). Так, для построения точек пересечения прямой a(a»,a’) общего положения с поверхностью прямого кругового конуса (рис. 12.8, г) показано использование плоскости общего положения α, проходящей через вершину конуса и заданную прямую. Плоскость задана двумя пересекающимися прямыми. Одна из них – это заданная прямая a(a»,a’), вторая – пересекающаяся с ней произвольная прямая b(b»,b’), проходящая через вершину конуса. Для построения проекций образующих, вдоль которых плоскость пересекает поверхность конуса, найден ее горизонтальный след, затем проекции C’ и D’ точек его пересечения с горизонтальным следом основания конуса и фронтальные проекции C» и D» этих точек. Искомые проекции точек M(M»,M’) и N(N»,N’) пересечения заданной прямой общего положения с поверхностью конуса находятся в местах пересечения с ней построенных образующих.

Аналогичные действия выполнены и для построения проекций M»,M’ и N»,N’ точек пересечения прямой общего положения k(k»,k’) с поверхностью наклонного эллиптического цилиндра (рис. 12.8, д). Для этого использовалось задание плоскости общего положения α(k∩l) также двумя пересекающимися прямыми, одна из которых, как и в предыдущем случае, – это заданная прямая k(k»,k’), а пересекающаяся с ней в произвольной точке 1(1″,1′) вторая прямая линия – это прямая l(l»,l’), параллельная образующим цилиндра. Строился горизонтальный след этой плоскости и по точкам пересечения его с горизонтальным следом заданного цилиндра находились образующие, по которым вспомогательная плоскость общего положения α(k∩l) пересекает цилиндр. В местах пересечения с проекциями этих образующих проекций прямой общего положения k(k»,k’) находятся искомые проекции M»,M’ и N»,N’ точек пересечения заданной прямой с поверхностью цилиндра.

Видео:Определение видимости.Скачать

Касательные плоскости и нормаль к поверхности

Плоскостью, касательной к поверхности в некоторой ее точке, называют плоскость, в которой можно провести две прямые линии, пересекающиеся в точке касания, касательные к двум пересекающимся в этой же точке линиям, принадлежащим поверхности.

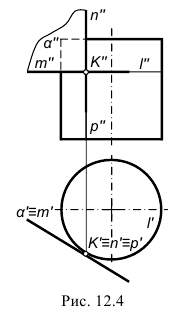
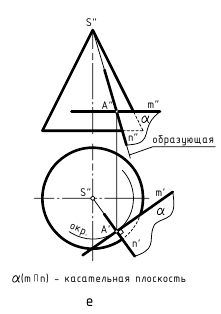
На чертеже касательную плоскость α(α»,α’) однозначно можно задать проекциями двух пересекающихся прямых m(m»,m’) и n(n»,n’). Эти линии строят касательно к проекциям двух пересекающихся в точке касания линий, принадлежащих поверхности. На рис. 12.4 линия m(m»,m’) является касательной к линии окружности l(l»,l’), проходящей через точку касания K(K»,K’) по поверхности цилиндра, а пересекающаяся с ней в этой точке линия n(n»,n’) сливается с линией р(р»,р’) – образующей цилиндра.

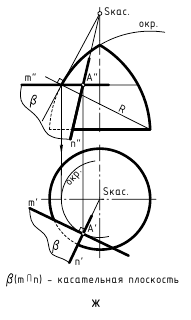
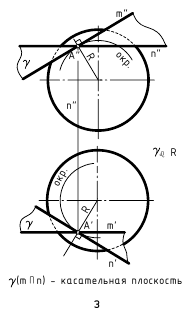
Аналогичные действия (рис. 12.8, е, ж, з) выполнены и при построении касательных плоскостей к поверхностям прямого кругового конуса, самопересекающегося тора и сферы, касающихся этих поверхностей в некоторой точке A(A»,A’). Пересекающиеся прямые m(m»,m’) и n(n»,n’), задающие касательные плоскости α(α»,α’) к ним, являются касательными к окружностям, построенным на этих поверхностях вращения и пересекающимся в точке касания A(A»,A’). Следует отметить одну особенность при построении прямой n(n»,n’), касательной к линии меридионального сечения поверхности самопересекающегося тора (рис. 12.8, ж). Для упрощения построений вначале строят касательную к этой линии, параллельной фронтальной плоскости проекций, определяют на оси вращения тора точку S, через которую проходят касательные ко всем точкам, расположенным на той же параллели поверхности, что и заданная точка касания A(A»,A’), а затем строят необходимую касательную n(n»,n’).

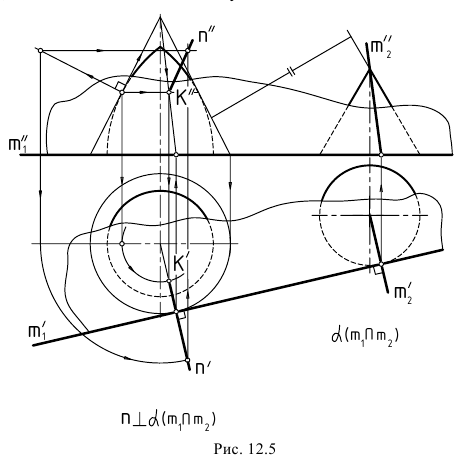
Эти построения использовались также для определения точки касания K(K»,K’) на поверхности самопересекающегося тора в задаче на рис. 12.5, где необходимо было задать общую касательную плоскость к поверхностям самопересекающегося тора и прямого кругового конуса. Ключом к решению задачи явилось заключение самопересекающегося тора в коническую поверхность с тем же углом наклона образующих, что и у заданного конуса (справа). Общая касательная плоскость задана пересекающимися прямыми, из которых m₁(m₁«,m₁‘), являющаяся горизонтальным следом плоскости, построена, как касательная к следам указанных конических поверхностей, а прямая m₂(m₂«,m₂‘), сливается с одной из образующих заданного конуса. Эта образующая является и геометрическим элементом касания построенной плоскости α(m₁∩m₂) с поверхностью заданного конуса. Поверхности самопересекающегося тора эта плоскость касается в точке K(K»,K’), которая найдена благодаря вышерассмотренным построениям и образующей второго конуса, охватывающего тор.

На рассматриваемом чертеже показано также построение нормали n(n»,n’), к поверхности самопересекающегося тора в точке K(K»,K’). Условием для построения нормали является ее перпендикулярность к плоскости, касательной к поверхности в той же точке. Вначале нормаль построена к очерковой образующей тора, затем на ней взята произвольная точка и выполнен ее поворот вокруг оси тора в положение, в котором она окажется расположенной в плоскости, перпендикулярной построенной касательной плоскости (направления указанных перемещений показаны стрелками).

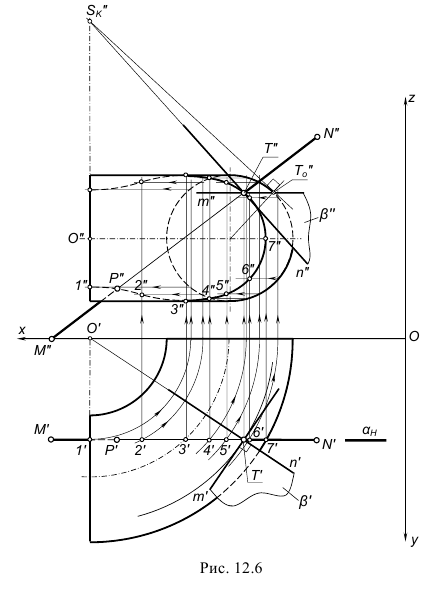
На рис. 12.6 показано построение точек пересечения P(P»,P’) и T(T»,T’) фронтальной прямой MN(M»N»,M’N’) с поверхностью ¼ кольцевого тора и построение касательной плоскости к этой поверхности в одной из построенных точек, например, T(T»,T’).

Точки P(P»,P’) и T(T»,T’) найдены благодаря заключению заданной прямой MN во фронтальную плоскость α(α_H) и построению проекций линии пересечения по точкам 1′, 2′, 3′, … , 7′, крайние из которых 1′ и 7′ взяты в местах пересечения горизонтального очерка плоскостью тора, а остальные – произвольно на горизонтальном следе α_H секущей плоскости. Для дальнейших построений использовались горизонтальные сечения поверхности тора плоскостями.

Для задания касательной плоскости β(m∩n) одна из задающих ее пересекающихся прямых m(m»,m’) построена как касательная к линии кольцевого сечения поверхности тора в точке T(T»,T’), а вторая – как касательная прямая n(n»,n’) к линии окружности осевого сечения поверхности тора. Для более точного построения второй прямой была найдена проекция S_K» точки на оси вращения тора, в которой сходятся все касательные прямые к поверхности тора во всех точках, находящихся на той же параллели, что и точка T(T»,T’).

Структуризация материала двенадцатой лекции в рассмотренном объеме схематически представлена на рис. 12.7 (лист 1). На последующем листе 2 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 12.8).

Пересечение линии с поверхностью:

Касательные плоскости и нормаль к поверхности

Касательная плоскость к кривой поверхности в некоторой точке – это плоскость, в которой лежат все касательные прямые ко всем кривым, которые можно провести на поверхности через ту же точку.

Нормалью к поверхности в данной точке называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

12.1. Пересечение прямой с поверхностью

12.2. Касательные плоскости

• Проецирование прямой
• Взаимное положение плоскостей, прямой линии и плоскости
• Взаимное расположение точки, прямых и плоскостей
• Перпендикулярность геометрических объектов
• Прямая в пространстве и ее изображение на чертеже
• Многогранники
• Поверхности вращения
• Пересечение прямой линии с поверхностью

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Пересечение прямой и плоскостиСкачать

Линия пересечения плоскостей онлайн

С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Начертательная геометрия Лекция №8 ( 2 часть ) Пересечение поверхностейСкачать

Линия пересечения плоскостей − теория, примеры и решения

Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.

Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α₁ и α₂:

Найдем уравнение линии пересеченя плоскостей α₁ и α₂. Для этого рассмотрим следующие случаи:

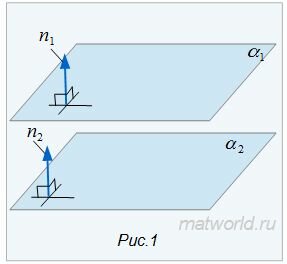Умножив уравнение (2) на λ, получим:

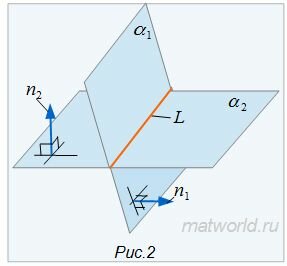Если векторы n₁ и n₂ не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:

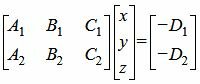(4)

Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.

Так как в системе линейных уравнений (4) векторы n₁=<A₁, B₁, C₁> и n₂=<A₂, B₂, C₂> не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:

,

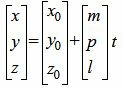(5)

Равенство (5) можно записать в следующем виде:

.

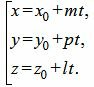(6)

Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α₁ и α₂. Полученное уравнение прямой можно записать в каноническом виде:

.

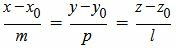Пример 1. Найти линию пересечения плоскостей α₁ и α₂:

Поскольку направляющие векторы n₁ и n₂ неколлинеарны, то плолскости α₁ и α₂ пересекаются.

Для нахождения линии пересечения влоскостей α₁ и α₂ нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:

.

(9)

Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:

.

(10)

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строку 2 со строкой 1, умноженной на −2:

.

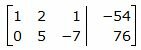Второй этап. Обратный ход Гаусса.

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:

.

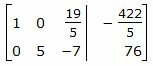Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

.

.

(11)

где t− произвольное действительное число.

Запишем (11) в следующем виде:

.

(12)

Получили уравнение линии пересечения плоскостей α₁ и α₂ в параметрическом виде. Запишем ее в каноническом виде.

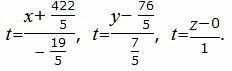(13)

Из равентсв выше получим каноническое уравнение прямой:

Ответ. Уравнение линии пересечения плоскостей α₁ и α₂имеет вид:

Пример 2. Найти линию пересечения плоскостей α₁ и α₂:

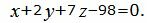(14)

(15)

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/2), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/2:

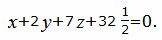(16)

Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α₁ и α₂ не совпадают. Следовательно они параллельны, т.е. не пересекаются.

Пример 3. Найти линию пересечения плоскостей α₁ и α₂:

(17)

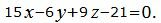(18)

Поскольку направляющие векторы n₁ и n₂ коллинеарны (n₁ можно получить умножением n₂ на число 1/3), то плоскости α₁ и α₂ параллельны или совпадают.

При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α₂ умножив на число 1/3:

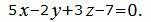(19)

Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α₁ и α₂ совпадают.

🔥 Видео

Пересечение прямой линии с плоскостью Определение видимости прямойСкачать

Построение линии пересечения плоскостейСкачать

Как строить сечения тетраэдра и пирамидыСкачать

Построение линии пересечения двух треугольников.Скачать

Котика ударило током, 10 т. ВольтСкачать

Нахождение пересечения двух треугольниковСкачать

Линия пересечения двух поверхностей конус и цилиндр (Метод секущих плоскостей)Скачать

Начертательная геометрия. 1 урок. Метод конкурирующих точекСкачать

Лекция 12. Пересечение поверхностей метод плоскостейСкачать

Построение линии пересечения двух плоскостейСкачать