Рассчитать длину окружности арки (6 видео)

ПК РАДИУС

Содержание

Гибочный калькулятор
Введите значения H и h в миллиметрах
Формула Пепина для расчёта длины дуги АРКИ
Калькулятор расчета радиуса лучковой арки
Цены на кирпич
Калькулятор расчета радиуса лучковой арки
Пояснения по проведению расчета
🔍 Видео

Видео:+Как найти длину окружностиСкачать

Гибочный калькулятор

Чаще всего стоит задача определения параметров дуги по её габаритным размерам. Для этого мы предлагаем гибочный калькулятор.

Видео:Длина окружности. Математика 6 класс.Скачать

Введите значения H и h в миллиметрах


хорда	H = мм
высота хорды	h = мм
радиус	R = 0 мм
длина дуги	L = 0 мм
угол сегмента	φ = 0 градусов
Очистить	Вычислить	Сохранить расчёт

Не забывайте, что для гибки профилей необходим технологический припуск от 500 до 1000 мм. на заготовку.

Вы можете скачать ПК версию гибочного калькулятора по этой ссылке.

140030, МО, Люберецкий район, пос. Малаховка, Касимовское шоссе, д. 3Г, кор.1.

тел. на время пандемии — 8 (985) 310-57-57 с 9:00 до 18:00 по рабочим дням

Видео:КАК ИЗМЕРИТЬ ДЛИНУ ОКРУЖНОСТИ? · ФОРМУЛА + примеры · Длина окружности как найти? Математика 6 классСкачать

Формула Пепина для расчёта длины дуги АРКИ

Формула Пепина для расчёта длины дуги АРКИ.

На днях исполнится мне 54 года. На очереди 54 статья по счётчику «Прозы». В свёртке число 54 даёт простое число 9 – точно такое же число получается при свёртке моего полного настоящего ФИО. Пришла идея «отметить» такое совпадение чисел интересной статьёй. Решил опубликовать мою формулу для расчета длины дуги арки. (Первую арку я изготовил, как ни странно, тоже 9 лет назад.)
Кому это нужно?
Это нужно таким же, как я людям, которые при изготовлении металлоизделий: арочных козырьков, беседок, теплиц и разного рода крыш — сталкиваются с необходимостью расчетов заготовок для гнутья дуг, скажем из профильной трубы разного размера.
Арки из металлопрофиля изготавливаются прокатыванием металла в трёхвалковых вальцах. За счёт многократного прокатывания «туда-обратно» прямая заготовка металла приобретает форму части дуги окружности. Дуга получается, конечно, неточной геометрической копией части окружности. Но вполне достаточным приближением к окружности. Точность зависит от нескольких факторов: от однородности трубы, от степени износа валов вальцов, от расстояния между валами вальцов и от количества проходов – количества раз прокатывания « туда-обратно». Ну, и конечно от искусства и навыков изготовителя.
Но моя идея состоит в том, что если знать длину заготовки металла для конкретной дуги, то при прокатывании заготовки нужно только замерять расстояние между концами заготовки. И когда при изготовлении дуги расстояние между концами заготовки совпадёт с размером основания дуги (прямой, ограничивающей сегмент дуги снизу), то дуга обретает заданные размеры, она готова.
Но как рассчитать длину дуги, когда обычно для козырька или беседки задаются величина основания сегмента дуги и высоте дуги? Хорошо, если уже есть готовый чертёж, который нарисован архитектором, дизайнером или рекламщиком. Там хотя бы есть радиус дуги. И тогда можно на подходящей поверхности начертить часть окружности с таким радиусом. При изготовлении первых дуг так приходилось делать: чертить дугу на земле или на полу. И замерять длину заготовки для дуги, прикладывая к нарисованной дуге рулетку. Потом отрезать заготовку такой длины и прокатывать до совпадения с размером основания сегмента дуги.
Глядя на то, как красиво вырисовываются дуги в графических редакторах на компьютере, мне всё время думалось, что должна быть такая формула, по которой можно высчитать длину дуги, зная только размеры основания и высоты дуги. Перекопав доступную литературу по математике и по строительству, я не смог найти такую формулу. НО думаю, что, наверное, она где-то есть. Поэтому решил попробовать самому вывести эту формулу. Благо дети учились в старших классах школы и были учебники по геометрии. И… Вот, с помощью учебника геометрии 10 или 11 класса, точно уже не помню, мне удалось вывести такую формулу. Само доказательство, даже уже приготовленное в виде статьи ещё году в 2005-ом, сгинуло вместе со всей информацией, когда «сдох» очередной жёсткий диск компьютера, но сам способ вычисления длины дуги сегмента остался в виде алгоритма записанного в рабочей тетради, благодаря тому, что я этим алгоритмом постоянно пользуюсь.
Вот этот метод вычисления длины дуги по основанию и высоте дуги и свою формулу я предлагаю всем заинтересованным людям.
Посмотрим на рисунок. Допустим нам нужно найти длину верхней дуги изображённой арки. Рисуем на этой арке прямоугольный треугольник. Одним катетом является высота арки – это катет b (катет противолежащий углу альфа). Он же является частью радиуса. Второй катет – a (катет прилежащий к углу альфа), является половиной основания сегмента арки.
Исходя из величин катетов этого треугольника, мы можем найти длину дуги арки (сегмента) по формуле (3) , которую я нескромно назвал формулой Пепина. (3)
Как видим, для получения величины длины дуги нам нужно знать угол альфа. Величину этого угла мы можем найти через отношение известных нам размеров катетов, то есть через тангенс угла альфа. Для этого мы согласно формуле (1) поделим величину катета b на величину катета a.
Сократив (округлив) полученное значения тангенса до тысячной мы по сокращённой таблице тангенсов Брадиса, приведённой на рисунке, находим значение угла альфа. В колонках tg ; приведена только дробная часть тангенса (для простоты отброшено 0 целых). Как показывает мой опыт, что для удовлетворительной точности изготовления дуги достаточно знать величину градуса с десятой частью угла. Но у нас таблица только с целыми значениями градусов. Если привести с десятыми, то величина таблицы увеличиться тоже в 10 раз. Мне показалось, что тогда долго искать придётся. Желающие, конечно, могут взять полную таблицу тангенсов Брадиса и пользоваться ей. Я поступаю, так нахожу десятую часть градуса с помощью прикидки «в уме». Между целыми градусами разница от 18 до 34 тысячных градуса. Разделив эту разницу на 10, я получаю значение тангенса для десятой доли угла альфа. И уже, прикинув, сколько не хватает или лишку до ближайшего целого градуса, я нахожу десятичное значение градуса угла альфа. Кто-то, может быть, построит себе таблицу с точностью до десятой доли градуса.

Далее нам нужно рассчитать величину радиуса дуги R. Для этого выведена формула (2)

Далее, значения угла альфа и радиуса подставляем в формулу Пепина (3) и получаем длину дуги. Потом, режем заготовку металла такой длины и прокатываем до тех пор, пока расстояние между концами заготовке не станет равным величине основания дуги.
Прежде чем рассмотреть конкретный пример, напомню, что если у вас дуга равна точно полуокружности, то вы можете воспользоваться классической формулой длины окружности которая равна Пи R (полуокружность).
Рассмотрим пример. Пусть у нас высота арки 87 сантиметров , а ширина (величина основания сегмента 256 сантиметров ( 2 метра 56 сантиметров)

Шаг 1. Формула (1)
Ищем тангенс угла альфа. Для этого поделим 87 сантиметров на половину основания, то есть на 128 сантиметров. Получаем 0,6796875. Округляя до тысячной – получаем 0, 680. Это значение попадает между 34 и 35 градусами. Между ними разница в 25 «единиц». Значит одной десятой градуса соответствует 2, 5 «единицы». Между значением 34 градуса = 0, 675 и полученными 0, 680 всего пять «единиц». 5 «единиц» поделим на 2, 5 и получаем, что к 34 градусам нужно добавить 2 десятых градуса. Значит, искомая величина угла альфа равна 34, 2 градуса.

Шаг 2. (Формула (2)
Вычисляем значение радиуса. Катет b = 0.87 метра, В квадрате это будет 0,7569. Катет a = 1.28 метра, следовательно, в квадрате это будет =1, 6384. Сумма квадратов катетов = 2,3953. Теперь это число поделим на удвоенный катет b , что соответствует 1.74 метра. Получаем в результате значения радиуса равное 1.3766.. метра. Нас устроит такое значение, и даже значение 1,38 метра.
Шаг 3 Формула (3)
Подставляем полученные значения в формулу Пепина.
Угол 34,2 градуса помножаем на радиус 1.38 метра и помножаем на коэффициент 0.07 (семь сотых) и получаем величину длины дуги = 3, 30372… Для практических целей берём заготовку длиной 3 метра 30 сантиметров.
Практически у каждых вальцов дуга не прокатывает самые концы дуги из-за того, что между валами вальцов есть расстояние. У меня на небольших вальцах это непрокатываемое расстояние всего по семь сантиметров с каждого конца. На качество изделия эти прямые части не влияют. Поэтому я беру заготовки по рассчитанной по формуле (3) величине. Тем, кто хочет иметь более полное соответствие дуги геометрии окружности, или у кого большие не прокатываемые концы, то для этого следует к рассчитанной длине дуги прибавить удвоенное расстояние не прокатываемого конца, и замерять величину основания с учетом (вычетом) этого удлинения заготовки.
Всем успехов в работе и построение арок, которые находят всё большее и большее применение в нашей жизни!
Жжуков Иван. 20 октября 2012 года. г. Орёл.

Дня через два опубликую эту статью на сайте Гайдпарк, там она будет иметь более удобный для чтения вид.

Видео:Как Найти Радиус Сегмента на Потолке. Радиус Окружности По Хорде И Высоте СегментаСкачать

Калькулятор расчета радиуса лучковой арки

Согласитесь, очень элегантно в интерьере или в оформлении территории участка смотрятся арочные конструкции. Их широко применяют при кладке печей и каминов, уличных комплексов барбекю, при оформлении проходов между комнатами, при строительстве заборов, беседок и других сооружений. Но качественно выложить арку – задача весьма непростая, требующая немалой сноровки и обязательной выверки каждого производимого действия.

Калькулятор расчета радиуса лучковой арки

Чтобы арка не получилась непрочной или перекошенной, необходимо строго контролировать ее размерные параметры. Определиться с некоторыми из них – проблем особых нет: например, ширина проема легко промеряется или задается заранее, высоту свода обычно выбирают, исходя из дизайнерской задумки или доступности свободного места. Но как точно определить радиус той дуги, что будет задавать нижний свод арки? Нет никаких проблем, если арка полуциркульная, то есть составляет ровно половину окружности – ее радиус в этом случае равен половине ширины проема. А как быть с лучковой?

Цены на кирпич

Предлагаем не искать геометрические формулы в интернете, а применить размещенный в данной публикации калькулятор расчета радиуса лучковой арки. Несколько пояснений будут даны ниже.

Калькулятор расчета радиуса лучковой арки

Пояснения по проведению расчета

Для возведения арки обычно заранее готовят шаблон – так называемое кружало. Чтобы оно в точности соответствовало необходимой «геометрии», без знания радиуса дуги, образующей свод арки, никак не обойтись. Кроме того, необходимо, чтобы линии швов между кирпичами, создающими арочный свод, сходились точно в одной точке – в центре той окружности, частью которой является дуга. Для этого в этом центре забивают гвоздь, к нему привязывают нитку, и по ней выверяют правильность направления каждого шва кладки. Но чтобы безошибочно наметить этот центр, опять же не обойтись без значения радиуса.

Все швы, между кирпичами, образующими арочный свод, должны «смотреть» в одну центральную точку, и это обязательно при кладке контролируется натянутой из этого центра ниткой

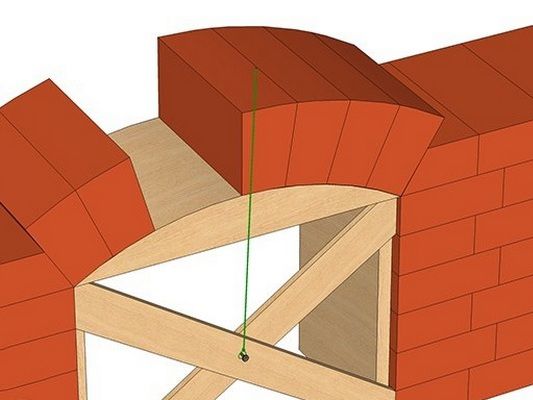
Итак, обычно в распоряжении мастера имеются две «стартовых» величины:

Схема, которая поможет правильно определиться с исходными размерными параметрами арки

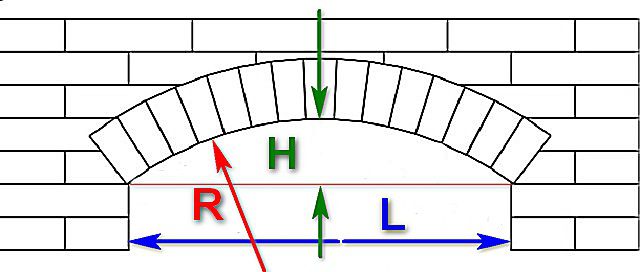
L – так называемая длина арки, то есть расстояние между ее крайними точками по горизонтали. Обычно это будет ширина дверного проема или, например, ширина каминного топочного окна.

Н – высота арки, то есть расстояние по вертикали от горизонтальной линии (хорды), соединяющей ее крайние нижние точки, и самой верхней точкой свода.

Существует геометрическая зависимость, по которой, основываясь на этих двух величинах, можно точно рассчитать и радиус дуги, задающей нижний свод арки (R). Эта формула заложена в предлагаемый калькулятор.

Необходимо всего лишь последовательно указать на слайдерах значения длины и высоты арки – и программа сразу даст ответ с точностью до миллиметра.

Внимание – исходные данные указываются также в миллиметрах.

Сложно ли построить камин для дома самостоятельно?

Безусловно, это задача повышенного уровня сложности, но если есть навыки в выполнении качественной кирпичной кладки, то почему бы не попробовать? Возьмите, например, несложную схему-порядовку, которая приведена в статье нашего портала, посвященной выбору и строительству дровяных каминов для дома .