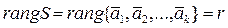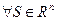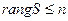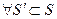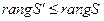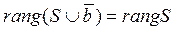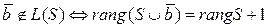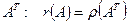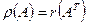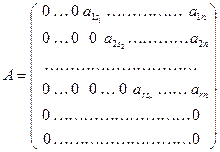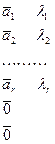Ранг системы векторов свойства ранга

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4

В пространстве R n любая линейно независимая система, имеющая n векторов, является базисом этого пространства.

Пусть`a 1,`a 2 , ¼ ,`a n — линейно независимая система векторов пространства R n, а`e 1,`e 2 , … ,`e n — стандартный базис этого пространства. Тогда`a 1,`a 2 , ¼ ,`a n Î L (`e 1, `e 2 , … ,`e n ) = R n. Согласно теореме о замене можно все векторы`e 1,`e 2 , …,`e n заменить на векторы`a 1,`a 2 , ¼,`a n , так что L (`a 1,`a 2 , ¼ ,`a n ) = L (`e 1,`e 2 , … ,`e n ) = R n. Следовательно, для системы векторов`a 1,`a 2 , ¼ ,`a n оба условия из определения базиса выполняются, и она является базисом пространства R n.

Видео:19. Ранг матрицы. Ранг системы векторовСкачать

6. БАЗИС И РАНГ СИСТЕМЫ ВЕКТОРОВ.

Базисом системы векторов называется ее подсистема (часть системы), которая удовлетворяет двум условиям:

– эта подсистема линейно независима;

– любой вектор исходной системы может быть представлен в виде линейной комбинации векторов этой подсистемы.

1) Базис является максимальной линейно независимой подсистемой векторов данной системы.

2) Любая система векторов, имеющая хотя бы один ненулевой вектор, обладает базисом.

3) Все базисы данной системы векторов имеют одинаковое количество векторов.

Эти свойства предлагается доказать в качестве упражнения.

Рангом системы векторов называется число r, равное количеству векторов в каком – либо базисе этой системы. Иными словами, рангом системы векторов называется максимальное количество линейно независимых векторов данной системы.

`b 1,`b 2 ,…,`b r (b) базисы соответствующих систем, получим

Ранг подсистемы не превышает ранга системы векторов.

2) Если`a 1,`a 2 , ¼ ,`a k Î L, dim L = m, r — ранг системы`a 1,`a 2 , ¼ ,`a k , то r £ m. Доказательство аналогично доказательству свойства 1).

3) Если количество векторов в системе векторов больше ранга этой системы, то данная система векторов является линейно зависимой.

Пусть`a 1,`a 2 , ¼ ,`a r — подсистема, являющаяся базисом данной системы векторов. Поскольку количество векторов в системе векторов больше ранга этой системы, то в данной системе существует хотя бы один вектор, не вошедший в указанный базис. Этот вектор линейно выражается через базис, и, следовательно, исходная система линейно зависима в силу критерия линейной зависимости.

Видео:Ранг матрицыСкачать

7. КООРДИНАТЫ ВЕКТОРА В ДАННОМ БАЗИСЕ.

Рассматривая понятия базисов подпространства, пространства R n, системы векторов, заметим, что во всех случаях базис обладает свойством линейной независимости и способностью представлять в виде линейных комбинаций своих векторов векторы подпространства, пространства R n, системы векторов соответственно. Докажем единственность такого представления.

Любой вектор`x (подпространства, пространства R n, системы векторов) представляется в виде линейной комбинации базисных векторов единственным образом.

Пусть`a 1,`a 2 , ¼ ,`a k — данный базис. Предположим, что существуют два различных представления вектора`x в виде линейной комбинации базисных векторов:

Поскольку`x –`x =`0, то

(l 1 – m 1) `a 1 + (l 2 – m 2 )`a 2 + … + (l k – m k )`a k =`0, откуда, в силу линейной независимости базисных векторов следует, что

l 1 – m 1 = 0, l 2 – m 2 = 0, …, l k – m k = 0 и, следовательно,

l 1 = m 1, l 2 = m 2, … , l k = m k. Таким образом, рассмотренные разложения вектора`x по базису совпадают. Теорема доказана.

Справедливость доказанного утверждения позволяет дать следующее определение.

Координатами вектора`x в данном базисе называются коэффициенты в разложении вектора`x по данному базису.

Заметим, что координаты вектора`x в данном базисе определяются однознач — но, но в разных базисах один и тот же вектор`x имеет разные координаты.

Видео:Ранг матрицыСкачать

§ 2. ОБЫКНОВЕННЫЕ ЖОРДАНОВЫ ИСКЛЮЧЕНИЯ ( ОЖИ )

Видео:Линейная алгебра, 6 урок, Ранг матрицыСкачать

1. ЖОРДАНОВЫ ТАБЛИЦЫ И ИХ ТРАКТОВКА.

Пусть имеется две системы переменных x 1, x 2, … , x n и y 1, y 2 , … , y m , которые связаны между собой соотношениями:

Эти соотношения можно записать в виде таблицы

Видео:Как найти ранг матрицы (пример) - bezbotvyСкачать

86. Ранг системы векторов и ранг матрицы. Основная теорема о двух системах векторов

Теорема 1. Пусть даны две системы векторов A1, A2, . AK, и B1, B2, . BM, которые обладают свойствами:

1) первая система линейно независима;

2) каждый вектор первой системы линейная комбинация векторов второй системы.

Тогда k £ m, т. е. число векторов первой системы не больше числа векторов второй системы.

Доказательство. Доказательство проводим методом математической индукции по числу векторов второй системы, т. е. по M.

Пусть M=1. Докажем, что K=1. Допустим противное, что K>1. Тогда по второму условию каждый вектор системы A1, A2, . AK линейно выражается через вектор B1, т. е. AI = aIBI ; I=1,2. K, где все числа aI ≠ 0 ; I=1,2. K. Действительно, в противно случае какой-нибудь вектор AI = 0 и по свойству система A1, A2, . AK линейно зависим, что противоречит условию. Тогда из первых двух равенств первой системы получаем, что

Отсюда вектора A1, A2 образуют линейно зависимую подсистему системы векторов A1, A2, . AK, что противоречит свойству. Установленное противоречие доказывает справедливость теоремы при M=1.

Предположим, что утверждение теоремы справедливо для любой системы второго вида, содержащей M — 1 вектор, и докажем его для системы содержащей M векторов. По второму условию имеем систему K равенств :

Видео:Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Ранг и базис конечной системы векторов

Определение. Рангом конечной системы векторов S называется максимальное число линейно независимых векторов данной системы.

1) , которая содержит r линейно независимых векторов.

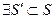
2) Любая 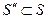, которая содержит больше чем r векторов, является линейно зависимой.

Свойства

Û

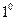
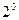
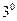
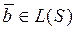
Определение. Элементарными преобразованиями системы векторов называются:

1) умножение какого-либо вектора системы на число, не равное нулю;

2) прибавление к какому-либо вектору системы другого вектора той же системы;

3) перестановка векторов местами;

4) вычеркивание (исключение) из системы вектора, являющегося линейной комбинацией остальных векторов системы;

5) приписывание к системе (ее пополнение) вектора, являющегося линейной комбинацией каких-либо векторов системы.

Определение. Подсистему данной конечной системы S будем называть базисом этой системы, если выполняются следующие условия:

1. — линейно независима

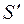
2. Каждый вектор системы S линейно выражается через систему .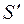

Свойства

Любая конечная система векторов S, содержащая хотя бы один ненулевой вектор, имеет базис.

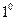
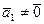
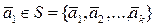
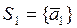
Пусть для определенности вектор . Тогда система —линейно независима.

Рассмотрим 2 возможные ситуации:

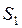
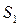
1. Каждый вектор системы S линейно выражается через систему ,следовательно, система -базис.

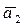
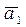
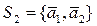
2. Некоторый вектор нельзя линейно выразить через вектор , следовательно — линейно независима.

Для системы 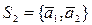рассмотрим 2 возможные ситуации:

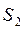
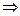
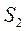
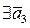
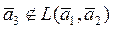
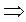
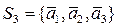
а) Каждый вектор системы S линейно выражается через систему система — базис.

б) , такой что — линейно независима и т.д.

Процесс выбора базиса завершится, так как S конечна. Свойство доказано.

Любые два базиса данной системы S имеют одинаковое число векторов.

Ранг данной системы векторов равен количеству векторов любого базиса данной системы.

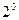
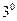
Пусть B – произвольный базис системы S. Тогда .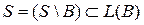

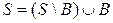
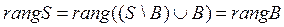
Так как , то по свойству 5) элементарных преобразований системы векторов .

Ранг матрицы

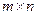
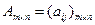
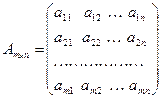
Определение. Напомним, что матрицей размера ( ) называется прямоугольная таблица чисел вида

.

В случае, когда значения m и n совпадают, матрицу будем называть квадратной матрицей порядка n:

.

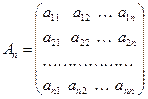
Частным случаем матрицы размера является случай, когда одно из значений m или n равно 1: или , то есть матрица представляет из себя вектор-столбец или вектор-строку соответственно.

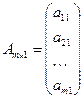
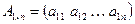
В общем случае каждая строка матрицы представляет собой n-мерный вектор, каждый столбец – m-мерный.

Транспонированной матрицей будем называть матрицу вида:

.

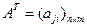
Единичной матрицей будем называть квадратную матрицу вида: , .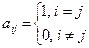

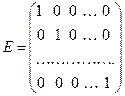
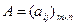
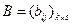
Рассмотрим матрицы и . Матрицы A и B будем называть равными, если они одинакового размера, и равны их соответствующие элементы.

Определение. Элементарными строчечными (столбцовыми) преобразованиями матрицы являются:

1. умножение строки (столбца) на число отличное от нуля;

2. перестановка местами строк (столбцов);

3. прибавление одной (-ого) строки (столбца) к другой (-ому) строке (столбцу);

4. исключение строки (столбца), являющейся (являющегося) линейной комбинацией остальных строк (столбцов) матрицы;

5. включение строки (столбца), являющейся (являющегося) линейной комбинацией остальных строк (столбцов) матрицы.

Замечание. Если матрица A есть расширенная матрица некоторой системы линейных уравнений, то элементарные преобразования ее строк в точности соответствуют элементарным преобразованиям уравнений системы.

Определение. Строчечным (столбцовым) рангом матрицы A будем называть максимальное число линейно независимых вектор-строк (вектор-столбцов) матрицы.

Теорема. При любых элементарных строчечных преобразованиях матрицы строчечный и столбцовый ранги не меняются.

Теорема. Строчечный и столбцовый ранги матрицы равны.

,

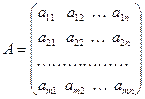
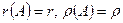
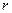
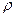
где и — строчечный и столбцовый ранги.

Доказать: .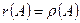

Приведем матрицу A с помощью элементарных строчечных преобразований к ступенчатому виду. Исключая из получившейся матрицы нулевые строки (если такие есть), получаем матрицу В.

.

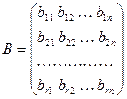
Поскольку столбцы матрицы В являются векторами r-мерного пространства, получаем (с учетом предыдущей теоремы) последовательно:

(1)

(2)

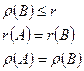
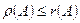
Поскольку полученное неравенство справедливо для произвольной матрицы А, применяя те же рассуждения к А Т , получаем:

(3)

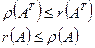
На основе (2) и (3) можно сделать вывод о том, что: .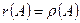

Следствие. .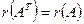

Определение. Ступенчатой матрицей будем называть матрицу, удовлетворяющую следующим условиям:

1. если в i-ой строке матрицы первый ненулевой элемент стоит на k-ом месте, то в (i+1)-ой строке первые k элементов нули;

2. если i-ая строка – нулевая, то (i+1)-ая строка также нулевая.

Замечание. Именно к такому, т.е. ступенчатому, виду мы приводили расширенную матрицу системы линейных уравнений в методе Гаусса.

Теорема. Ранг ступенчатой матрицы равен числу ее ненулевых строк.

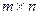
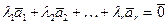
Рассмотрим матрицу A порядка , приведенную к ступенчатому виду:

(*)

💡 Видео

11. Ранг матрицыСкачать

Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

§26 Свойства ранга матрицыСкачать

Примеры Линейная зависимость векторов Базис и ранг системы векторовСкачать

Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

Лекция 11.2. Ранг матрицы. Метод окаймляющих миноровСкачать

Линейная зависимость векторов. РангСкачать

Линейная зависимость и линейная независимость векторов.Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Линейная зависимость векторовСкачать

Система векторов: линейная зависимость и независимость, базис, ранг | 5 | Константин Правдин | ИТМОСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Тимашев Д. А. - Алгебра, Часть 1. Лекции - 3. Системы векторов в векторном пространствеСкачать