Радиусы концентрических окружностей равны 9 и 12 найдите

Вопрос по геометрии:

Радиусы концентрических окружностей равны 9 см и 12 см. Найдите площадь кольца, ограниченного этими окружностями 1)42π см2 2)27π см2 3)63π см2 4)9π см2

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Ответы и объяснения 1

Площадь меньшей окружности = pi*r²=pi*9²=81*pi,
площадь большей=pi*R²=pi*12²=144*pi,
площадь кольца = 144*pi-81*pi=63*pi (см²)

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

• Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
• Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
• Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

• Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
• Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
• Использовать мат — это неуважительно по отношению к пользователям;
• Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Геометрия.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Геометрия — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения.

Видео:Радиус и диаметрСкачать

Радиусы концентрических окружностей равны 9 см и 12 см?

Геометрия | 5 — 9 классы

Радиусы концентрических окружностей равны 9 см и 12 см.

Найдите площадь кольца, ограниченного этими окружностями 1)42π см2 2)27π см2 3)63π см2 4)9π см2.

Площадь меньшей окружности = pi * r² = pi * 9² = 81 * pi,

площадь большей = pi * R² = pi * 12² = 144 * pi,

площадь кольца = 144 * pi — 81 * pi = 63 * pi (см²).

Видео:Найти центр и радиус окружностиСкачать

Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13и12 см?

Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусами 13и12 см.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Найти площадь кругового кольца, ограниченного двумя концентрическими окружностями радиусов 4, 5м и 6, 5?

Найти площадь кругового кольца, ограниченного двумя концентрическими окружностями радиусов 4, 5м и 6, 5.

Видео:Задача 6 №27642 ЕГЭ по математике. Урок 81Скачать

Радиусы двух концентрических окружностей относятся как 3 : 7?

Радиусы двух концентрических окружностей относятся как 3 : 7.

Найдите диаметры этих окружностей, если ширина кольца, образованного ими, равна 24 см.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 41 / √п и 37 / √п?

Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 41 / √п и 37 / √п.

Видео:Геометрия Радиус окружности, описанной около треугольника MKP равен 5 см SinM = 0,7 Найдите сторонуСкачать

Радиусы двух концентрических окружностей, относятся как 3 : 7?

Радиусы двух концентрических окружностей, относятся как 3 : 7.

Найдите радиусы этих окружностей, если ширина кольца, образованного ими, равна 16 см.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать

2)площадь кольца, ограниченного двумя окружностями общим центром, равна 45 п мв квадрате, а радиус меньшей окружности равен 3 м ?

2)площадь кольца, ограниченного двумя окружностями общим центром, равна 45 п мв квадрате, а радиус меньшей окружности равен 3 м .

Найдите радиус большей окружности.

Видео:Длина окружности. Математика 6 класс.Скачать

Площадь кольца ограниченного двумя окружностями с общим центром равна 45п м(квадрат), а радиус меньшей окружности равен 3 м?

Площадь кольца ограниченного двумя окружностями с общим центром равна 45п м(квадрат), а радиус меньшей окружности равен 3 м.

Найдите радиус большей окружности.

Видео:Геометрия 9 класс (Урок№10 - Взаимное расположение двух окружностей.)Скачать

Площадь кольца, ограниченного двумя концентрическими окружностями равна 1200π , а площади этих окружностей относятся как 11 : 12?

Площадь кольца, ограниченного двумя концентрическими окружностями равна 1200π , а площади этих окружностей относятся как 11 : 12.

Найдите радиус БОЛЬШЕЙ из окружностей.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Площадь кругового кольца, заключенного между 2мя окружностями с одним и тем же центром, равна 12см в квадрате?

Площадь кругового кольца, заключенного между 2мя окружностями с одним и тем же центром, равна 12см в квадрате.

Найдите площади этих кругов, ограниченных этими окружностями, если радиус одной из них в 2 раза больше, чем радиус другой.

Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусом 25см и 24см?

Найдите площадь кольца, ограниченного двумя окружностями с общим центром и радиусом 25см и 24см.

Вы находитесь на странице вопроса Радиусы концентрических окружностей равны 9 см и 12 см? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

Предположим, что 0 0 Если брать другой промежуток, то может быть и отрицательное значение. Cos2a = 2cos²a — 1 1 + tg²a = 1 / cos²a 1 / (1 + tg²a) = cos²a 2cos²a = 2 / (1 + tg²a) 2cos²a — 1 = 2 / (1 + tg²a) — 1 cos2a = 2 / (1 ..

1. Спирогира одна из наиболее распространенных водорослей пресных вод всех частей света, встречается также и в солоноватых водах. Спирогира образует большие ватообразные скопления, которые плавают на поверхности воды или стелются по дну и очень част..

Не понял, что именно надо найти, но : #1 угол АВС равен 180° — 67°32, по свойству смежных углов, угол АВС равен 112, 68° #2 угол 4 равен углу , по свойству вертикальных углов, угол 1 равен 180° — 37° = 143° по свойству смежных углов, угол 3 равен 143..

Координаты векторов АВ(6 ; 8) ВА( — 6 ; — 8).

Пусть переменная х — меньший угол, а 4х — больший угол а сумма этих смежных углов 180 тогда имеем уравнение вида : х + 4х = 180 5х = 180 х = 36 = меньший угол = >больший угол = = 4 * 36 = 144 угол, образующийся за счет биссектрис смежных углов = поло..

M = (a + b) / 2 m = (7 + 12) / 2 m = 9. 5 скобки не нужны.

Видео:9 класс, 24 урок, Формулы для вычисления площади правильного многоугольника, его стороныСкачать

Урок геометрии в 9 классе по теме «Длина окружности и площадь круга»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Видео:№567. Найдите образующую усеченного конуса, если радиусы оснований равны 3 см и 6 см, а высота равнаСкачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся

Сертификат и скидка на обучение каждому участнику

Выберите документ из архива для просмотра:

Выбранный для просмотра документ Список класса — шаблон.docx

Зачетная ведомость по теме: «Длина окружности и площадь круга»

1 уровень: 3 ряд

2 уровень: 2 ряд

2 уровень: 1 ряд

Выбранный для просмотра документ задачи.docx

1. Найдите углы правильного двадцатиугольника.

2. Длина окружности, описанного около квадрата, равна 7. Найдите периметр квадрата.

3. Радиусы концентрических окружностей равны 8 см и 9 см. Найдите площадь кольца, ограниченного этими окружностями.

1. Найдите углы правильного пятнадцатиугольника.

2. Длина окружности, описанного около квадрата, равна 9. Найдите площадь квадрата.

3. Радиусы концентрических окружностей равны 6 см и 7 см. Найдите площадь кольца, ограниченного этими окружностями.

1. Найдите углы правильного девятиугольника.

2. Длина окружности, вписанного в квадрат, равна 7. Найдите периметр квадрата.

3. Радиусы концентрических окружностей равны 6 см и 7 см. Найдите площадь кольца, ограниченного этими окружностями.

1. Найдите углы правильного тридцатиугольника.

2. Длина окружности, вписанного в квадрат, равна 9. Найдите площадь квадрата.

3. Радиусы концентрических окружностей равны 9 см и 12 см. Найдите площадь кольца, ограниченного этими окружностями.

1. Найдите сумму углов правильного десятиугольника.

2. Хорда окружности, равная 10 см, стягивает дугу в 90°. Найдите радиус окружности.

3. В окружность радиуса 6 см вписан правильный треугольник. Найдите площадь треугольника.

1. Найдите сумму углов правильного семиугольника.

2. Хорда окружности, равная 8 см, стягивает дугу в 120°. Найдите диаметр окружности.

3. В окружность радиуса 10 см вписан правильный треугольник. Найдите площадь треугольника.

1. Найдите длину окружности, в которую вписан квадрат со стороной 4 см.

2. Площадь круга равна 8 см 2 . Найдите длину окружности, ограничивающей данный круг.

3. В окружность радиуса 12 см вписан правильный треугольник. Найдите площадь треугольника.

1. Найдите площадь правильного шестиугольника, если радиус вписанной окружности равен 3см, сторона 6см.

2. Площадь кругового сектора равна 8 см 2 . Найдите радиус окружности, если центральный угол 45°.

3. Длина дуги окружности равна 3 см. Найдите градусную меру дуги, если радиус окружности 2 см.

1. Найдите площадь кругового сектора, ограниченного дугой в 30° и радиуса 12 см.

2. Найдите длину дуги окружности радиуса 4 см, если ее градусная мера равна 45°.

3. Периметр правильного треугольника, вписанного в окружность, равен 9 см. Найдите радиус окружности.

1. Найдите градусную меру дуги окружности, если площадь кругового сектора равна , а радиус 2.

2. Найдите площадь правильного четырехугольника, если радиус описанной около него окружности равен 2 см.

3. Углы правильного многоугольника равны 150°. Найдите число сторон этого многоугольника .

1. Найдите длину окружности, в которую вписан квадрат со стороной 3 см.

2. Из круга, радиус которого 8 см, вырезан сектор с дугой 30°. Найдите площадь оставшейся части круга.

3. Углы правильного многоугольника равны 156°. Найдите число сторон этого многоугольника .

1. Найдите длину окружности, в которую вписан правильный треугольник со стороной 3 см.

2. Из круга, диаметр которого 8 см, вырезан сектор с дугой 45°. Найдите площадь оставшейся части круга.

3. Найдите площадь кольца, ограниченного двумя концентрическими окружностями радиусов 3 и 4.

Выбранный для просмотра документ урок в 9 классе по геометрии 2016.docx

Муниципальное автономное образовательное учреждение

Полевского городского округа

«Средняя общеобразовательная школа — лицей № 4 «Интеллект»

Урок математики в 9 классе

по теме: «Длина окружности и площадь круга»

Бажова Наталья Михайловна,

высшей квалификационной категории

Полевской, 2016 г.

ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА

Тема урока : Длина окружности и площадь круга

Цель урока : Повторить понятия длины окружности и площади круга, закрепить способы их вычисления (по формулам).

Планируемые образовательные результаты :

– образовательные (формирование познавательных УУД, в том числе специально-предметных действий): научить выделять и формулировать познавательную цель,

систематизировать и обобщить знания и умения использования формул при решении задач;

– воспитательные (формирование личностных и коммуникативных УУД): анализировать, сравнивать и обобщать факты, строить логически обоснованное рассуждение, использовать математическую речь. Самостоятельно организовывать взаимодействие в паре, отстаивать свою точку зрения.

– развивающие (формирование регулятивных УУД): постановка учебных задач, формировать умения обрабатывать информацию и систематизировать ее по указанным основаниям; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Методы и формы обучения : индивидуальная работа

Технология : уровневой дифференциации, критериального оценивания

Образовательные ресурсы :fipi.ru (ФИПИ открытый банк заданий по математике)

Основные термины и понятия : длина окружности, площадь кругового сектора, радиус окружности, диаметр круга, центральный угол, длина дуги, правильный n -угольник, формулы для вычисления элементов правильного n -угольника через радиус вписанной и описанной окружности.

1. Найдите углы правильного двадцатиугольника.

2. Длина окружности, описанного около квадрата, равна 7. Найдите периметр квадрата.

3. Радиусы концентрических окружностей равны 8 см и 9 см. Найдите площадь кольца, ограниченного этими окружностями.

1. Найдите углы правильного пятнадцатиугольника.

2. Длина окружности, описанного около квадрата, равна 9. Найдите площадь квадрата.

3. Радиусы концентрических окружностей равны 6 см и 7 см. Найдите площадь кольца, ограниченного этими окружностями.

1. Найдите углы правильного девятиугольника.

2. Длина окружности, вписанного в квадрат, равна 7. Найдите периметр квадрата.

3. Радиусы концентрических окружностей равны 6 см и 7 см. Найдите площадь кольца, ограниченного этими окружностями.

1. Найдите углы правильного тридцатиугольника.

2. Длина окружности, вписанного в квадрат, равна 9. Найдите площадь квадрата.

3. Радиусы концентрических окружностей равны 9 см и 12 см. Найдите площадь кольца, ограниченного этими окружностями.

1. Найдите сумму углов правильного десятиугольника.

2. Хорда окружности, равная 10 см, стягивает дугу в 90°. Найдите радиус окружности.

3. В окружность радиуса 6 см вписан правильный треугольник. Найдите площадь треугольника.

1. Найдите сумму углов правильного семиугольника.

2. Хорда окружности, равная 8 см, стягивает дугу в 120°. Найдите диаметр окружности.

3. В окружность радиуса 10 см вписан правильный треугольник. Найдите площадь треугольника.

1. Найдите длину окружности, в которую вписан квадрат со стороной 4 см.

2. Площадь круга равна 8 см 2 . Найдите длину окружности, ограничивающей данный круг.

3. В окружность радиуса 12 см вписан правильный треугольник. Найдите площадь треугольника.

1. Найдите площадь правильного шестиугольника, если радиус вписанной окружности равен 3см, сторона 6см.

2. Площадь кругового сектора равна 8 см 2 . Найдите радиус окружности, если центральный угол 45°.

3. Длина дуги окружности равна 3 см. Найдите градусную меру дуги, если радиус окружности 2 см.

1. Найдите площадь кругового сектора, ограниченного дугой в 30° и радиуса 12 см.

2. Найдите длину дуги окружности радиуса 4 см, если ее градусная мера равна 45°.

3. Периметр правильного треугольника, вписанного в окружность, равен 9 см. Найдите радиус окружности.

1. Найдите градусную меру дуги окружности, если площадь кругового сектора равна , а радиус 2.

2. Найдите площадь правильного четырехугольника, если радиус описанной около него окружности равен 2 см.

3. Углы правильного многоугольника равны 150°. Найдите число сторон этого многоугольника .

1. Найдите длину окружности, в которую вписан квадрат со стороной 3 см.

2. Из круга, радиус которого 8 см, вырезан сектор с дугой 30°. Найдите площадь оставшейся части круга.

3. Углы правильного многоугольника равны 156°. Найдите число сторон этого многоугольника .

1. Найдите длину окружности, в которую вписан правильный треугольник со стороной 3 см.

2. Из круга, диаметр которого 8 см, вырезан сектор с дугой 45°. Найдите площадь оставшейся части круга.

3. Найдите площадь кольца, ограниченного двумя концентрическими окружностями радиусов 3 и 4.

Критерии оценки самостоятельных работ учащихся с 1-12 вариант

Критерии оценивания выполнения задания

Ход решения задачи, получен верный ответ

Ход решения верный ,все его шаги присутствуют, но допущена описка или ошибка вычислительного характера

Другие случаи ,не соответствующие указанным критериям

Критерии оценивания выполнения задания

Ход решения задачи, получен верный ответ

Ход решения верный ,все его шаги присутствуют, но допущена описка или ошибка вычислительного характера

Другие случаи ,не соответствующие указанным критериям

Критерии оценивания выполнения задания

Ход решения задачи, получен верный ответ

Ход решения верный ,все его шаги присутствуют, но допущена описка или ошибка вычислительного характера

При правленом ходе решения задача не доведена до конца или ответ недостаточно обоснованный

Другие случаи ,не соответствующие указанным критериям

Критерии оценки самостоятельных работ учащихся с 13-14 варианта

Задание № 1,2 оценивается в 1 балл

Критерии оценивания выполнения задания

Ход решения задачи, получен верный ответ

Ход решения верный ,все его шаги присутствуют, но допущена описка или ошибка вычислительного характера

При правленом ходе решения задача не доведена до конца или ответ недостаточно обоснованный

Другие случаи ,не соответствующие указанным критериям

Нормы выставления оценок по группам

урока в соответствии с требованиями ФГОС (формирование УУД)

Тема урока : Длина окружности и площадь круга

Тип урока : Урок повторения предметных ЗУНов

Дидактическая задача урока :

Цели и задачи урока : выделение универсальных и специальных предметных учебных действий, формируемых в процессе изучения темы;

Планируемые образовательные результаты:

– образовательные (формирование познавательных УУД): научить выделять и формулировать познавательную цель; систематизировать и обобщить знания и умения использования формул при решении задач.

– воспитательные (формирование личностных и коммуникативных УУД): действие смыслообразования (установление связей между целями и мотивами), формирование умений слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, формировать коммуникативную компетенцию учащихся, воспитывать ответственность и аккуратность;

– развивающие (формирование регулятивных УУД): постановка учебных задач, формировать умения обрабатывать информацию и систематизировать ее по указанным основаниям; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.

Методы и формы обучения: индивидуальная работа

Технология: уровневой дифференциации, критериального оценивания

(заинтересованность учебным материалом, нестандартной формой урока, создание ситуации успеха и т.д.)

— ученик осознает, несколько важен для него учебный материал;

— деятельность не мотивирована

Формулировка цели учителем или детьми и способы фиксации цели урока. Приемы обучения, демонстрирующие недостаточность имеющихся знаний, несформированность УУД.

(сформулирована или создана проблемная ситуация, выдвигались гипотезы и др.)

— определяются учителем в готовом виде;

— согласуются в обсуждении с учениками;

— данный этап урока отсутствует

— тема урока: определяются учителем в готовом виде

— цель урока: определяются учителем в готовом виде, учениками выдвигаются гипотезы

— задачи урока: согласуются в обсуждении с учениками

— результат деятельности: согласуются в обсуждении с учениками;

3. Выработка плана (алгоритма) учебной деятельности

— используется предложенный учителем;

— выбирается из нескольких, предложенных учителем

— выбирается из нескольких, предложенных и учителем и учениками

— создается из предложенных учениками

Выбирается алгоритм учебной деятельности из нескольких уровней предложенных заданий учителем.

Формирование УУД в условиях решения практических задач

Овладение = усвоение УУД + применение ЗУНов в условиях решения практических задач

4. Характер учебной деятельности

Безошибочное выполнение упражнений, решение задач отдельными учениками, коллективом класса; безошибочные устные ответы; умение находить и исправлять ошибки.

5. Уровень самостоятельности обучающихся

-самостоятельны в выполнении заданий;

— испытывают серьезные затруднения в самостоятельном выполнении заданий;

— не могут справиться без помощи учителя

Самостоятельное решение задач (выполнение упражнений), выбор сложности заданий учениками. Самостоятельное нахождение и исправление ошибок

6. Методика формирования УУД (роль используемой технологии, методов, приемов, выбранная форма урока, форма учебного взаимодействия и т.п)

— формирование УУД целенаправленно и системно;

— формирование УУД эпизодично, бессистемно;

— формирование УУД не ведется

1.Приемы обучения учащихся работе с источниками информации

2.Формирование УУД целенаправленно и систематично

3.Приемы индивидуальной помощи учащимся со стороны учителя и одноклассников (непосредственные и опосредованные с помощью пособий)

7. Система оценивания достижений обучающихся:

— включение учащихся в обсуждение ответа;

— самооценка учащихся на основе словесной характеристики оценки

— ученики оценивают результат и процесс деятельности;

— самооценка результата и деятельности и д.р

— оценки объявляет учитель, комментируя их;

— оценки объявляет учитель, не комментируя их;

— оценки обсуждаются и определяются с учениками

Обучение способам контроля и самооценки деятельности. Умение учащихся самостоятельно находить и исправлять ошибки, определять степень успешности

Проявляется в устных высказываниях детей и в результатах письменных работ.

8. Результативность урока:

— ученики высказываются по поводу результатов урока;

— оценивают результат и процесс деятельности;

— объективно анализируют результаты урока и определяют значение результатов деятельности;

— самооценка результата и деятельнности

— результаты урока совпадают с целью урока и запланированными результатами

— результаты урока не совпадают с целью урока и запланированными результатами

Подведение итогов совместной и индивидуальной деятельности учеников (новое содержание, изученное на уроке и оценка личного вклада в совместную учебную деятельность), достижение поставленной цели

🎦 Видео

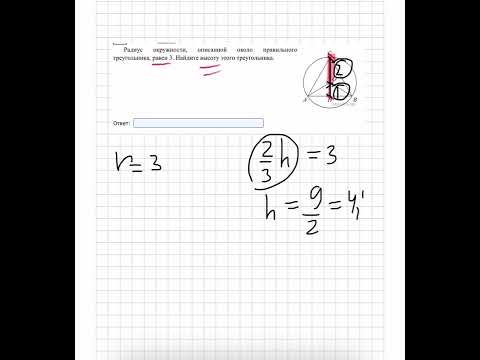
Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту треугольникаСкачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

Задача 6 №27859 ЕГЭ по математике. Урок 104Скачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия 9 класс. Радиус описанной и вписанной окружности треугольника. Формулы радиуса.Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать