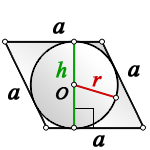
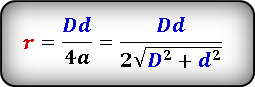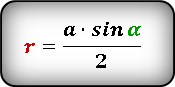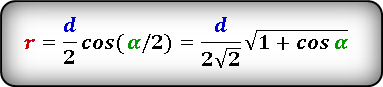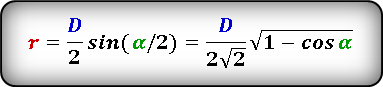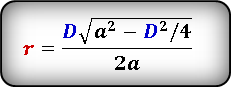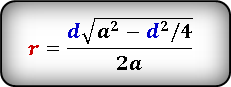С помощю этого онлайн калькулятора ромба можно найти высоту ромба по известным элементам. Для нахождения высоты ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
- 1. Высота ромба через сторону и площадь
- 2. Высота ромба через сторону и угол
- 3. Высота ромба через диагонали
- 4. Высота ромба через угол и противолежащую диагональ
- 5. Высота ромба через угол и диагональ из данного угла
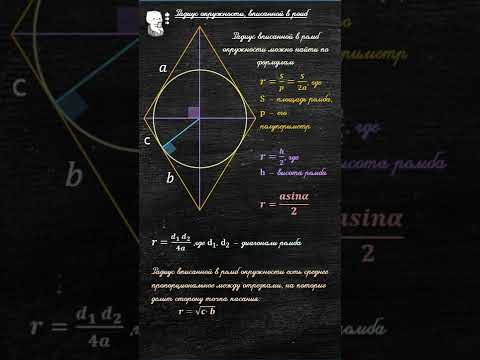
- 6. Высота ромба через радиус вписанной в ромб окружности
- Нахождение радиуса вписанной в ромб окружности
- Формулы вычисления радиуса вписанной в ромб окружности
- Через диагонали и сторону
- Через диагонали
- Через сторону и угол
- Через высоту
- Примеры задач
- Радиус вписанной окружности в ромб
1. Высота ромба через сторону и площадь
Пусть задан ромб (Рис.1).
 |
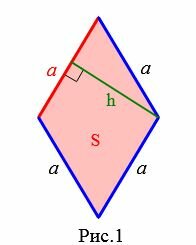Формула площади ромба через сторону и высоту имеет следующий вид:
| (small S=a cdot h.) |
Откуда легко вывести формулу высоты ромба через сторону и площадь:
| (small h=frac.) |
2. Высота ромба через сторону и угол
Рассмотрим ромб со стороной a и углом α между сторонами (Рис.2). Выведем формулу вычисления высоты ромба через сторону и угол.
 |
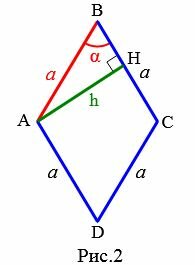Проведем высоту AH. Для прямоугольного треугольника AHB применим теорему синусов:
| (small frac=frac.) | (1) |
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
| (small h=a cdot sin alpha.) | (2) |
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого угла. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: (small angle C=180°-alpha.) Следовательно (small sin angle C=sin(180°-alpha)=sin alpha.) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
3. Высота ромба через диагонали
Выведем формулу вычисления высоты ромба через диагонали. Плошадь ромба через диагонали вычисляется формулой (см. статью Площадь ромба):
| (small S= frac,) | (3) |
а через сторону и высоту, формулой
| (small S= a cdot h.) | (4) |
Из формул (3) и (4) следует:
| (small frac=a cdot h.) | (5) |
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
 |
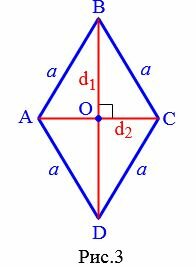Применим к прямоугольному треугольнику AOB теорему Пифагора:
| (small a^2= left( frac right)^2+left( frac right)^2.) | (6) |
| (small a= frac<sqrt> ) | (7) |
Подставим (7) в (5) и найдем h:
| (small frac=frac<sqrt> cdot h,) |
| (small h= frac <sqrt>.) | (8) |
4. Высота ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления высоты ромба.
 |
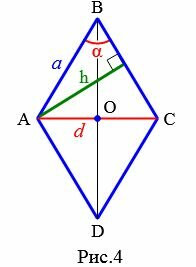Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Применим теорему синусов для прямоугольного треугольника AOB:
| (small frac=frac<large frac><large sin frac>.) |
| (small a=frac<large 2 cdot sin frac>.) | (9) |
С другой стороны (см. параграф 2):
| (small h=a cdot sin alpha.) | (10) |
Подставим (9) в (10):
| (small h=frac<large 2 cdot sin frac>.) | (11) |
Применяя формулу двойного угла для (small sin alpha, ) имеем: (small sin alpha=2 cdot sin frac cdot cos frac . ) Подставляя это равенство в формулу (11), получим формулу высоты ромба через угол и противолежащую диагональ:
| (small h=d cdot cos frac.) | (12) |
5. Высота ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
 |
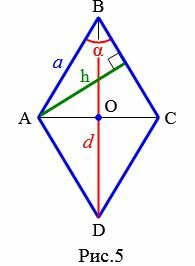Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Для прямоугольного треугольника AOB, имеем:
| (small frac =cos angle ABO.) | (13) |
Учитывая, что ( small BO=frac) и ( small angle ABO=frac), формулу (13) можно записать так:
| (small frac< large frac >= cos frac .) |
| (small a=frac<large 2 cdot cos large frac>.) | (14) |
Подставим (14) в (2):
| (small h= frac<large 2 cdot cos frac> .) |
или, учитывая что (small sin alpha=2 cdot sin frac cdot cos frac , ) получим:
| (small h= d cdot sin frac.) | (15) |
6. Высота ромба через радиус вписанной в ромб окружности
Покажем, что высота ромба через радиус вписанной окружности вычисляется по формуле:
| ( small h=2cdot r.) |
В статье Площадь ромба показали, что площадь ромба через сторону и высоту вычисляется формулой
| (small S= a cdot h.) | (16) |
а площадь ромба через сторону и радиус вписанной окружности − формулой:
Нахождение радиуса вписанной в ромб окружности
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить радиус окружности, вписанной в ромб. Также разберем примеры решения задач для закрепления изложенного материала.
Формулы вычисления радиуса вписанной в ромб окружности
Через диагонали и сторону
Радиус r вписанной в ромб окружности равняется произведению его диагоналей, деленному на сторону, умноженную на 4.
- d1 и d2 – диагонали ромба;
- a – сторона ромба.
Через диагонали
Радиус r вписанной в ромб окружности можно найти, зная только длины его обеих диагоналей:
Эту формулу можно получить, если сторону a в формуле выше выразить через диагонали (согласно одному из свойств ромба):
Через сторону и угол
Радиус окружности r, вписанной в ромб, равняется половине произведения его стороны и синуса любого угла.
Через высоту
Радиус вписанного в ромб круга равняется половине его высоты.
Примеры задач
Задание 1
Известно, что диагонали ромба равны 6 и 8 см. Найдите радиус окружности, вписанной в него.
Решение
Применим соответствующую формулу, подставив в нее известные значения:
Задание 2
Вычислите радиус вписанного в ромб круга, если его сторона равна 11 см, а один из углов – 30°.
Решение
В данном случае мы можем воспользоваться последней из рассмотренных выше формул:
Радиус вписанной окружности в ромб
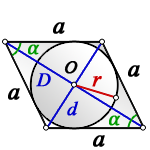
1. Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб через диагонали ( r ) :
Формула радиуса вписанной окружности в ромб через сторону и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и угол ( r ) :
Формула радиуса вписанной окружности в ромб через диагональ и сторону ( r ) :
2. Радиус вписанной окружности ромба, равен половине его высоты
a — сторона ромба
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в ромб ( r ) :