Радиус вписанной окружности в квадрат равен 56 корней из 2 (4 видео)

Радиус вписанной окружности в квадрат равен 56 корней из 2

Вопрос по математике:

Радиус окружности описанной около квадрата равен 56 корней из 2 найдите радиус окружности вписанной в этот квадрат

Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?

Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!

Содержание

Как написать хороший ответ?
Радиус вписанной окружности в квадрат равен 56 корней из 2
Радиусы описанной и вписанной окружностей в квадрат
Окружность вписанная в квадрат
Окружность описанная около квадрата
Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.
💥 Видео

Ответы и объяснения 1

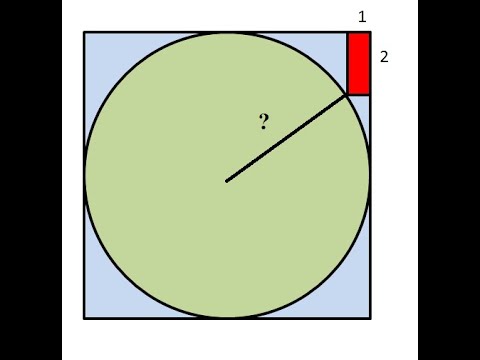
Радуис описанной около квадрата окружности совпадает с половиной диагонали, радиус вписанной — с половиной стороны. Так как диагональ к стороне относится как √2 : 1, то радиус вписанной окружности равен 56√2 : √2 = 56

Знаете ответ? Поделитесь им!

Как написать хороший ответ?

Чтобы добавить хороший ответ необходимо:

Отвечать достоверно на те вопросы, на которые знаете правильный ответ;
Писать подробно, чтобы ответ был исчерпывающий и не побуждал на дополнительные вопросы к нему;
Писать без грамматических, орфографических и пунктуационных ошибок.

Этого делать не стоит:

Копировать ответы со сторонних ресурсов. Хорошо ценятся уникальные и личные объяснения;
Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не знаю» и так далее;
Использовать мат — это неуважительно по отношению к пользователям;
Писать в ВЕРХНЕМ РЕГИСТРЕ.

Есть сомнения?

Не нашли подходящего ответа на вопрос или ответ отсутствует? Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие вопросы в разделе Математика.

Трудности с домашними заданиями? Не стесняйтесь попросить о помощи — смело задавайте вопросы!

Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

Радиус вписанной окружности в квадрат равен 56 корней из 2

Задание 17. Радиус окружности, описанной около квадрата, равен 6√2. Найдите радиус окружности, вписанной в этот квадрат.

Радиус описанной окружности равен половине диагонали квадрата (половина синей линии), то есть, диагональ, равна:

В свою очередь диагональ квадрата – это величина

где a – сторона квадрата. То есть,

Радиус вписанной окружности равен половине стороны квадрата (половина красной линии на рисунке). Получаем:

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Радиусы описанной и вписанной окружностей в квадрат

Видео:Сторона квадрата равна 56. Найдите радиус окружности, вписанной в этот квадрат.Скачать

Окружность вписанная в квадрат

Чтобы формула нахождения радиуса вписанной окружности в квадрат r была правильно рассчитана, необходимо изначально вспомнить какими свойствами обладает данная фигура. У квадрата:

все углы прямые, то есть, равны 90°;
все стороны, как и углы, равны;
диагонали равны, точкой пересечения бьются строго пополам и пересекаются под углом 90°.

При этом вписанная в выпуклый многоугольник окружность обязательно касается всех его сторон. Обозначим квадрат ABCD, точку пресечения его диагоналей O. Как видно на рисунке 1, пересечение линий АС и ВD дают равнобедренный треугольник АОВ, в котором стороны АО=ОВ, углы ОАВ=АВО=45°, а угол АОВ=90°. Тогда радиусом вписанной окружности в квадрат будет не что иное, как высота ОЕ полученного равнобедренного треугольника АОВ.

Если предположить, что сторона квадрата равна у, то формула нахождения радиуса вписанной окружности в квадрат будет выглядеть следующим образом:

Объяснение: в равнобедренном треугольнике АОВ высота ОЕ или радиус r делят основание АВ пополам (свойства), образовывая при этом прямоугольный треугольник с прямым угол ОЕВ. В маленьком треугольнике ЕВО основание ОВ образует со сторонами ОЕ и ЕВ углы по 45°. Значит треугольник ЕВО еще и равнобедренный. Стороны ОЕ и ЕВ равны.

Видео:Задание 16 ОГЭ по математике. Окружность описана около квадратаСкачать

Окружность описанная около квадрата

Вокруг квадрата также можно описать окружность. В этом случае каждая вершина фигуры будет касаться окружности. Следующая формула нахождения радиуса описанной окружности около квадрата будет находиться еще проще. В этом случае R описанной окружности будет равен половине диагонали квадрата. В буквенном виде формула выглядит так (рисунок 2):

Объяснение: после проведения диагоналей ABCD образовались два одинаковых прямоугольных треугольника АВС = CDA. Рассмотрим один из них. В треугольнике CAD:

угол CDA=90°;
стороны AD=CD. Признак равнобедренного треугольника;
угол DAC равен ACD. Они равны по 45°.

Чтобы найти в этом прямоугольном треугольнике гипотенузу АС, необходимо воспользоваться теоремой Пифагора:
, отсюда
Поскольку окружность касается вершин квадрата, а точка пересечения его диагоналей является центром описанной окружности (свойства), то отрезок ОС и будет радиусом окружности. Он является половинкой гипотенузы. Это утверждение вытекает из свойств равнобедренного треугольника или свойств диагоналей квадрата. Потому формула нахождения радиуса описанной окружности около квадрата в нашем случае имеет следующий вид:

Поскольку AD=CD, а свойства квадратного корня позволяют вынести одно из подкоренных выражений, тогда формула приобретает вид:

Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

Нахождения величины радиуса описанной окружности около квадрата при известной величине радиуса вписанной окружности.

треугольник ОСЕ – равнобедренный и прямоугольный;
ОЕ=ЕС=;
ОЕС=90°;
ЕОС=ОСЕ=45°;

Найти: ОС=?
Решение: в данном случае задачу можно решить, воспользовавшись либо теоремой Пифагора, либо формулой для R. Второй случай будет проще, поскольку формула для R выведена из теоремы.