Радиус окружности вписанной в треугольник равен 2 корня из 3

Геометрия | 5 — 9 классы

Радиус окружности, вписанной в равносторонний треугольник, равен 2 корня из 3 .

Найдите длину стороны этого треугольника.

Равносторонний треугольник — это правильный треугольник.

Для правильных многоугольников справедлива формула :

аn = 2R·sin(π / n) = 2r·tg(π / n), где R — радиус описанной окружности, r — радиус вписанной окружности

Для треугольника эти формулы выглядят так : an = 2Rsin60° = R√3

и аn = 2r·tg60° = 2r√3

В нашем случае r = 2√3, тогда а = 2· 2√3·√3 = 12.

R — радиус вписанной окружности.

Oтвет : сторона равностоннего треугольника равна 12 см.

Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Радиус окружности, вписанной в равносторонний треугольник равен 12 найдите высоту этого треугольника?

Радиус окружности, вписанной в равносторонний треугольник равен 12 найдите высоту этого треугольника.

Видео:2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3Скачать

Радиус окружности, вписанной в равносторонний треугольник, равен 12?

Радиус окружности, вписанной в равносторонний треугольник, равен 12.

Найдите высоту этого треугольника.

Видео:2071 радиус окружности вписанной в правильный треугольник равен корень из 3 на 2Скачать

Радиус окружности, вписанной в равносторонний треугольник, равен 14?

Радиус окружности, вписанной в равносторонний треугольник, равен 14.

НАЙТИ высоту этого треугольника.

Видео:Задача 6 №27909 ЕГЭ по математике. Урок 129Скачать

Радиус вписанной в равносторонней треугольник окружности равен 2 см?

Радиус вписанной в равносторонней треугольник окружности равен 2 см.

Найдите периметр треугольника.

Видео:Задача 6 №27910 ЕГЭ по математике. Урок 130Скачать

Найдите радиус окружности, вписанной в равносторонний треугольник со стороной 12 см?

Найдите радиус окружности, вписанной в равносторонний треугольник со стороной 12 см.

Видео:Задача 6 №27921 ЕГЭ по математике. Урок 138Скачать

Радиус окружности, описанной около равностороннего треугольника, равен 10√3?

Радиус окружности, описанной около равностороннего треугольника, равен 10√3.

Найдите длину стороны этого треугольника.

Видео:Радиус окружности, описанной около треугольника АВС, равен 2 корня из 3. Найдите АВ, если...Скачать

Найдите высоту равностороннего треугольника если радиус окружности вписанной в этот треугольник равен 8 см?

Найдите высоту равностороннего треугольника если радиус окружности вписанной в этот треугольник равен 8 см.

Видео:Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Равносторонний треугольник авс вписан в окружность радиуса 6 см ?

Равносторонний треугольник авс вписан в окружность радиуса 6 см .

Найдите его сторону.

Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Радиус окружности, вписанной в равносторонний треугольник, равен 12?

Радиус окружности, вписанной в равносторонний треугольник, равен 12.

Найдите высоту этого треугольника.

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Найдите площадь равностороннего треугольника, вписанного в окружность радиуса 4 корня из 3?

Найдите площадь равностороннего треугольника, вписанного в окружность радиуса 4 корня из 3.

Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Сторона равностороннего треугольника равна 20 корней из 3?

Сторона равностороннего треугольника равна 20 корней из 3.

Найдите радиус окружности, вписанной в этот треугольник.

Если вам необходимо получить ответ на вопрос Радиус окружности, вписанной в равносторонний треугольник, равен 2 корня из 3 ?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Геометрия вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

В прямоугольном ∆ АВС∠С = 90°, высота СК делит гипотенузу на отрезки АВ = 5 см, кВ = 1 см. Определите длину высоты СК. Высотапрямоугольноготреугольника, проведеннаяк гипотенузе, естьсреднеегеометрическое (среднеепропорциональное) между отрезками, н..

Видео:Задание 16 ОГЭ по математике. Две окружности одна описана около квадрата, другая вписана в него.Скачать

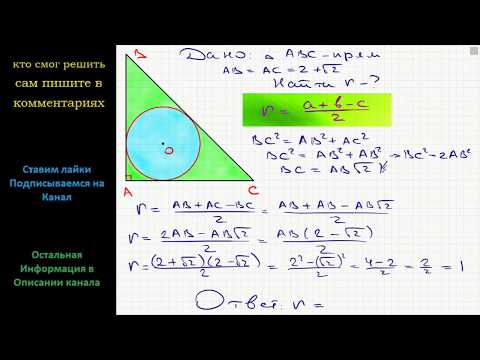
Треугольник с вписанной окружностью 2 корня из 3

Видео:ОГЭ 2020 задание 17Скачать

В прямоугольный треугольник с углом 60˚ вписана окружность, радиус равен 2√3см. Найдите площадь этого треугольника

Видео:Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать

Ваш ответ

Видео:15 задание треугольники огэ по математике / маттаймСкачать

решение вопроса

Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Похожие вопросы

• Все категории
• экономические 43,282
• гуманитарные 33,619
• юридические 17,900
• школьный раздел 606,997
• разное 16,829

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:Задача 6 №27892 ЕГЭ по математике. Урок 126Скачать

В окружности радиуса 2 корень из 3 вписан правильный треугольник?

Геометрия | 5 — 9 классы

В окружности радиуса 2 корень из 3 вписан правильный треугольник.

Найдите радиус окружности, вписанной в данный треугольник.

R = a / √3, r = a√3 / 2 / .

Видим, что радиус вписанной окружности в 2 меньше.

R = 2√3 / 2 = √3 — это ответ.

Первая окружность описана около треугольника, а вторая — вписана в него.

Видео:Задание 16 ОГЭ по математике. Окружность вписана в равносторонний треугольник.Скачать

Прямоугольные треугольник вписан в окружность радиуса 5см?

Прямоугольные треугольник вписан в окружность радиуса 5см.

В треугольник вписана окружность радиуса 1 см.

Найдите площадь треугольника.

Видео:2065 радиус окружности вписанной в правильный треугольник равен 29 Найдите высоту этого треугольникаСкачать

Правильный треугольник вписан в окружность радиуса 5 см?

Правильный треугольник вписан в окружность радиуса 5 см.

Определите радиус окружности, вписанной в этот треуг — к.

Видео:17 задание ОГЭ по математикеСкачать

Прямоугольный треугольник вписан в окружность радиуса 5см в треугольник вписана окружность радиуса 1см найдите площадь треугольника?

Прямоугольный треугольник вписан в окружность радиуса 5см в треугольник вписана окружность радиуса 1см найдите площадь треугольника.

Радиус окружности вписанной в правильный треугольник равен корень из трех деленый на два?

Радиус окружности вписанной в правильный треугольник равен корень из трех деленый на два.

Найдите сторону этого треугольника.

Правильный треугольник вписан в окружность, радиуса 6 см ?

Правильный треугольник вписан в окружность, радиуса 6 см .

Найдите периметр треугольника и радиус вписанной в него окружности.

В правильный треугольник со стороной а вписана окружность, найдите радиус?

В правильный треугольник со стороной а вписана окружность, найдите радиус.

В окружность вписан правильный шестиугольник?

В окружность вписан правильный шестиугольник.

В него вписана окружность, в которую вписан правильный треугольник.

Найдите радиус большей окружности, если сторона треугольника равна 1 см.

В окружность с радиусом R, вписан правильный треугольник?

В окружность с радиусом R, вписан правильный треугольник.

Найдите радиус окружности, вписанной в этот треугольник.

Правильный треугольник со стороной см вписан в окружность?

Правильный треугольник со стороной см вписан в окружность.

Найдите радиус этой окружности.

Правильный треугольник вписан в окружность радиуса 5см?

Правильный треугольник вписан в окружность радиуса 5см.

Определите радиус окружности, вписанной в этот треугольник.

На этой странице находится ответ на вопрос В окружности радиуса 2 корень из 3 вписан правильный треугольник?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.

Разделим диагональ на 2 : 12 / 2 = 6смпо теореме пифагора найдем половину другой диагонали : 10 ^ 2 — 6 ^ 2 = 100 — 36 = 64 корень из 64 = 8вторая диагональ равна 2 * 8 = 16 смплощадь ромба равна половине произведения его диагоналей, следовательно Sa..

1)P∆ACD = AC + CD + AD 24 = 10 + CD + AD CD + AD = 14 2)Pabcd = 2 * (AD + CD) = 2 * 14 = 28 Ответ : 28см.

В прямоугольном треугольнике SHO катет SO лежит напротив угла в 30°, значит SO = SH / 2 = 4 / 2 = 2. ОН² = SH² — SO² = 16 — 4 = 12, OH = 2√3. Точка О — центр квадрата, значит АВ = 2ОН = 4√3. Площадь основания So = AB² = 48. Площадь боковой поверх..

Если все боковые ребра наклонены под одним углом к основанию пирамиды, все боковые ребра равны, а вершина пирамиды проецируется в центр описанной около основания окружности. Центр окружности, описанной около прямоугольного треугольника лежит на сере..

4 см. Получается 4 см. Думаю объяснять не надо.

Y = x³ — 3x² / 3 — x ООФ : x≠3 y = x²(x — 3 / — (x — 3) = — x² , (x≠3) y = — x² , (x≠3) график парабола c вершиной в начале координат , ветвикоторой направлены вниз ; выколотая точка параболы сабсциссой x = 3.

Сторона ромба = √24 ^ 2 + 7 ^ 2 = √576 + 49 = √625 = 25 Ответ : 25.

Вот. Стороны равны Там теорема Пифагора и все рассписано.

X + x + x + 33 = 180 3x = 180 — 33 3x = 147 x = 49 49 и 49 — углы при основании 49 + 33 = 82 — угол при вершине.

Треугольник вписанный в окружность

Определение

Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.

На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.

ВD = FC = AE — диаметры описанной около треугольника окружности.

O — центр вписанной в треугольник окружности.

Формулы

Радиус вписанной окружности в треугольник

r — радиус вписанной окружности.

1. Радиус вписанной окружности в треугольник,
   если известна площадь и все стороны:

Радиус вписанной окружности в треугольник,
если известны площадь и периметр:

Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:

Радиус описанной окружности около треугольника

R — радиус описанной окружности.

1. Радиус описанной окружности около треугольника,
   если известна одна из сторон и синус противолежащего стороне угла:

Радиус описанной окружности около треугольника,
если известны все стороны и площадь:

Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:

Площадь треугольника

S — площадь треугольника.

1. Площадь треугольника вписанного в окружность,
   если известен полупериметр и радиус вписанной окружности:

Площадь треугольника вписанного в окружность,
если известен полупериметр:

Площадь треугольника вписанного в окружность,
если известен высота и основание:

Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:

Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:

[ S = frac ab cdot sin angle C ]

Периметр треугольника

P — периметр треугольника.

1. Периметр треугольника вписанного в окружность,
   если известны все стороны:
   

Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:

Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:

Сторона треугольника

a — сторона треугольника.

1. Сторона треугольника вписанного в окружность,
   если известны две стороны и косинус угла между ними:

Сторона треугольника вписанного в
окружность, если известна сторона и два угла:

Средняя линия треугольника

l — средняя линия треугольника.

1. Средняя линия треугольника вписанного
   в окружность, если известно основание:
   

Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:

Высота треугольника

h — высота треугольника.

1. Высота треугольника вписанного в окружность,
   если известна площадь и основание:

Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:

[ h = b cdot sin alpha ]

Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:

Свойства

• Центр вписанной в треугольник окружности
  находится на пересечении биссектрис.
• В треугольник, вписанный в окружность,
  можно вписать окружность, причем только одну.
• Для треугольника, вписанного в окружность,
  справедлива Теорема Синусов, Теорема Косинусов
  и Теорема Пифагора.
• Центр описанной около треугольника окружности
  находится на пересечении серединных перпендикуляров.
• Все вершины треугольника, вписанного
  в окружность, лежат на окружности.
• Сумма всех углов треугольника — 180 градусов.
• Площадь треугольника вокруг которого описана окружность, и
  треугольника, в который вписана окружность, можно найти по
  формуле Герона.

Доказательство

Около любого треугольника, можно
описать окружность притом только одну.

окружность и треугольник,
которые изображены на рисунке 2.

окружность описана
около треугольника.

1. Проведем серединные
   перпендикуляры — HO, FO, EO.
2. O — точка пересечения серединных
   перпендикуляров равноудалена от
   всех вершин треугольника.
3. Центр окружности — точка пересечения
   серединных перпендикуляров — около
   треугольника описана окружность — O,
   от центра окружности к вершинам можно
   провести равные отрезки — радиусы — OB, OA, OC.

окружность описана около треугольника,
что и требовалось доказать.

Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.

Радиус окружности вписанной в треугольник равен 2 корня из 3

Решение:
S=P*r/2 P=a+a+a=3a r=2√3 S=(a*a*sin60)/2=(a²√3)/4=(3a*2√3)/2 a=12 P=12+12+12=36

Пусть а см — сторона треугольника Площадь треугольника вписанного в окружность: S=P*r/2 Периметр треугольника со стороной а: P=a+a+a=3a r=2√3 Площадь равностороннего треугольника равна: S= (a²√3)/4 приравяв обе формулы получим: P*r/2 = (a²√3)/4 (3a*2√3)/2 = (a²√3)/4 3a√3 = (a²√3)/4 (сократим обе части на a√3) 3 = а/4 a=12 P=12+12+12=36 Ответ. Периметр треугольника = 36 см.