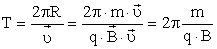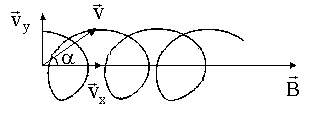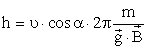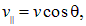Радиус окружности движения частицы в магнитном поле формула (8 видео)

Движение заряженных частиц в однородном магнитном поле

Начнём с простейшего случая — движения заряженной частицы вдоль линий индукции магнитного поля. При таком движении частицы угол а между векторами её скорости v и индукции В равен 0 или л. Поэтому по формуле (5.39) магнитная сила равна нулю, т.е. магнитное поле не действует на частицу. Она будет двигаться по инерции — равномерно и прямолинейно.

Пусть теперь частица, имеющая заряд q, движется перпендикулярно к линиям магнитной индукции (а = 7г/2) . Тогда магнитная сила равна

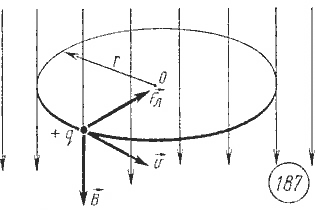
и направлена перпендикулярно векторам v и В (рис. 5.22). Следовательно, частица движется в плоскости, перпендикулярной к вектору магнитной индукции, причём сила F является центростремительной силой F_nc:

где т — масса заряженной частицы, а г — радиус кривизны её траектории.

Приравняв правые части (5.65) и (5.66), найдём радиус кривизны траектории

Так как в однородном поле В = const, а численное значение скорости заряда в магнитном поле не изменяется, то радиус кривизны траектории этого заряда оказывается постоянным. Поэтому заряженная частица будет двигаться по окружности, плоскость которой перпендикулярна к магнитному полю, а радиус прямо пропорционален скорости частицы и обратно пропорционален произведению её удельного заряда — на индукцию В поля.

Направление магнитной силы и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависит от знака заряда q частицы. Если частица движется в плоскости чертежа (рис. 5.23) слева направо, а магнитное поле направлено из-за чертежа перпендикулярно к его плоскости, то при q > 0 частица отклоняется вниз, а при q 2 = const). В этом уравнении — есть нормальное

ускорение а , модуль которого равен —. Модуль силы

в данном случае qvB . Заменив в (5.72) векторы их модулями, получим уравнение

Следовательно, для периода обращения частицы

Т — ^ пГ получается формула v

Таким образом, в релятивистском случае период обращения по мере увеличения скорости уменьшается. При v «с (5.74) переходит в (5.68).

Из предыдущего следует, что траекторию заряженных частиц можно формировать с помощью магнитного поля. Этот способ широко используется во всех современных ускорителях.

Видео:Движение заряженной частицы в магнитном поле | Физика ЕГЭ с Никитой АрхиповымСкачать

Движение заряженной частицы в магнитном поле.

Для вывода общих закономерностей движения заряженной частицы в магнитном поле будем считать магнитное поле однородным, электрические поля на частицу не действуют. При этом учтем очевидное:

а) Если заряженная частица движется в магнитном поле вдоль силовой линии, сила Лоренца, действующая на неё, равна нулю

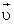
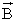
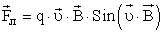
б) Если заряженная частица движется в магнитном поле со скоростью , перпендикулярно к вектору , то сила Лоренца, равная постоянна по модулю и перпендикулярна к траектории частицы.

Согласно второму закону Ньютона, эта сила создаёт центростремительное ускорение. Поэтому частица будет двигаться по окружности, радиус которой определяется из условия:

, , ,

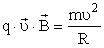
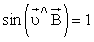
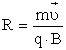
период вращения частицы, т. е. время, затрачиваемое ею на один полный оборот,

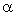
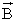
в) Если скорость заряженной частицы направлена под углом к вектору то её движение можно представить в виде двух движений: 1) равномерного прямолинейного движения вдоль поля, 2) равномерного движения по окружности в плоскости перпендикулярной полю (Рис. 23).

В результате этих двух движений возникает движение по винтовой линии, ось которой параллельна вектору 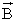. Шаг винтовой линии:

Направление, в котором закручивается частица, зависит от знака её заряда.

Действие магнитного поля на движущиеся заряженные частицы. Действие магнитного поля на проводник с током означает, что магнитное поле действует на движущиеся электрические заряды. Найдем силу, действующую на электрический заряд q при его движении в однородном магнитном поле с индукцией .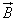
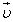
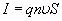
Сила тока I в проводнике связана с концентрацией n свободных заряженных частиц, скоростью их упорядоченного движения и площадью S поперечного сечения проводника следующим выражением:

,(1)

где q — заряд отдельной частицы.

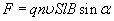
Так как произведение nSl равно числу свободных заряженных частиц в проводнике длиной l

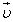
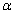
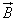
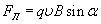
то сила, действующая со стороны магнитного поля на одну заряженную частицу, движущуюся со скоростью под углом к вектору индукции, равна

.(2)

Эту силу называют силой Лоренца.
Направление вектора силы Лоренца 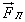определяется правилом левой руки, в нем за направление тока нужно брать направление вектора скорости положительного заряда (рис. 186). Для случая движения отрицательно заряженных частиц четыре пальца следует располагать противоположно направлению вектора скорости.

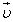
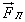
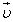
Движение заряженных частиц в магнитном поле. В однородном магнитном поле на заряженную частицу, движущуюся со скоростью перпендикулярно линиям индукции магнитного поля, действует сила , постоянная по модулю и направленная перпендикулярно вектору скорости (рис. 187).

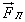
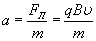
В вакууме под действием силы Лоренца частица приобретает центростремительное ускорение

(3)

и движется по окружности. Радиус r окружности, по которой движется частица, определяется из условия

, .(4)

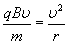
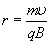
Период обращения частицы в однородном магнитном поле равен

.(5)

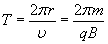
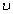
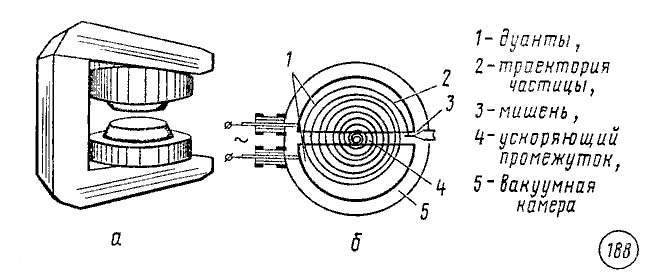
Последнее выражение показывает, что период обращения частицы в однородном магнитном поле при постоянной массе не зависит от скорости и радиуса r траектории ее движения. Этот факт используется, например, в ускорителе заряженных частиц — циклотроне.

Циклотрон. В этом ускорителе заряженные частицы — протоны, ядра атомов гелия — разгоняются переменным электрическим полем постоянной частоты в вакууме в зазоре между двумя металлическими электродами — дуантами. Дуанты находятся между полюсами постоянного электромагнита (рис. 188, а).

Под действием магнитного поля внутри дуантов заряженные частицы движутся по окружности. К моменту времени, когда они совершают половину оборота и подходят к зазору между дуантами, направление вектора напряженности электрического поля между дуантами изменяется на противоположное и частицы вновь испытывают ускорение. Каждую следующую половину оборота частицы пролетают по окружности все большего радиуса (рис. 188, б), но период их обращения остается неизменным. Поэтому для ускорения частиц на дуанты подается переменное напряжение с постоянным периодом.
Ускорение частиц в циклотроне с постоянным периодом возможно лишь до значений скоростей, значительно меньших скорости света. С приближением скорости частицы к скорости света в вакууме, равной c = 300000 км/с, масса частицы возрастает, вследствие чего увеличивается период ее обращения в магнитном поле. Равенство периода обращения частицы и периода изменения электрического поля нарушается, ускорение прекращается.

топлива по сравнению с обычной тепловой электростанцией.

В заключение, по традиции, предлагаем Вашему вниманию шпаргалку по этой теме:

Видео:Урок 276. Сила Лоренца. Движение заряженных частиц в магнитном полеСкачать

5.3. Движение заряда в однородном магнитном поле

Если начальная скорость заряженной частицы v перпендикулярна магнитному полю В, то в этом случае частица под действием силы Лоренца будет двигаться по окружности постоянного радиуса R (рис. 5.13)

Рис. 5.13. Движение отрицательно заряженной частицы в однородном магнитном поле

Сила Лоренца F_L, направленная по радиусу к центру окружности, вызывает радиальное ускорение. По второму закону Ньютона имеем

следовательно, можем записать уравнение

из которого легко получить выражение для угловой скорости частицы

Если q, m и B — постоянные величины, то угловая скорость, а следовательно, и период

тоже являются постоянными величинами, не зависящими от энергии частицы. От скорости движения частицы зависит только радиус орбиты

Сила Лоренца создает только нормальное ускорение и, соответственно, направлена к центру окружности. Следовательно, направление вращения положительно заряженной частицы таково, что вращающийся в том же направлении винт будет двигаться против направления поля. Отрицательно заряженная частица вращается в противоположном направлении (см. рис. 5.14, 5.15).

Рис. 5.14. Движение положительно и отрицательно заряженных частиц в однородном магнитном поле.
Направление магнитного поля указано точками

Если начальная скорость частицы параллельна вектору магнитной индукции, то сила Лоренца равна нулю. Частица будет продолжать двигаться в том же направлении прямолинейно и равномерно.

Наконец, в общем случае можно представить себе, что частица влетает в область однородного магнитного поля со скоростью v, составляющей угол q с направлением магнитного поля. Эту скорость можно разложить на компоненту две составляющих, одна из которых

направлена вдоль поля, а вторая

перпендикулярна полю. Соответственно, движение частицы является суммой двух движений: равномерного вдоль поля со скоростью и вращения по окружности с угловой скоростью . Траектория частицы, таким образом, является спиралью с радиусом R и шагом h (рис. 5.15):

Рис. 5.15. Движение заряженной частицы по спирали в однородном магнитном поле

Пример. В однородном магнитном поле с индукцией 2 Тл движется протон. Траектория его движения представляет собой винтовую линию с радиусом 10 см и шагом 60 см. Определить скорость и кинетическую энергию протона. Какую ускоряющую разность потенциалов U прошел протон перед тем, как влететь в магнитное поле?

Решение. Из уравнений (5.11) находим угол между скоростью протона и полем

Кинетическая энергия протона будет

Мы могли использовать нерелятивистскую формулу для энергии, так как скорость протона много меньше скорости света.

Если протон ускорялся электрическим полем, то при прохождении разности потенциалов U он приобрел энергию eU. Отсюда находим разность потенциалов

Джоуль — слишком большая энергия в мире элементарных частиц. Здесь используют внесистемную единицу — электронвольт (эВ).

Электрон-вольт (эВ) — это внесистемная единица энергии, численно равная энергии, которую приобретает электрон, пройдя ускоряющую разность потенциалов 1 В

Она удобна тем, что любая другая частица с зарядом по модулю равным заряду электрона, ускоренная разностью потенциалов в 3,66 МэВ, как в нашем примере, имеет кинетическую энергию 3,66 МэВ (мегаэлектронвольт).