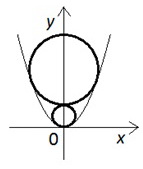Найдите все значения параметра а, при каждом из которых система 
имеет ровно 4 решения.
Первое уравнение задает части двух парабол (см. рисунок):
Второе уравнение задает окружность радиусом 
с центром 
На рисунке видно, что четыре решения системы получаются в двух случаях.
1. Окружность касается каждой из ветвей обеих парабол.
2. Окружность пересекает каждую из ветвей обеих парабол в двух точках, лежащих по разные стороны от оси абсцисс.
Составим уравнение для ординат общих точек окружности и параболы 
Получим: 
откуда
Чтобы окружность касалась парабол, уравнение должно иметь нулевой дискриминант: 
откуда
Во втором случае радиус окружности заключен между числами 3 и 9.
Ответ: 
| Критерии оценивания ответа на задание С5 | Баллы |
|---|---|
| Обоснованно получен верный ответ. | 4 |
| Рассмотрены все возможные случаи. Получен верный ответ, но решение либо содержит пробелы, либо вычислительную ошибку или описку. | 3 |
| Рассмотрены все возможные случаи. Получен ответ, но решение содержит ошибки. | 2 |
| Рассмотрены некоторые случаи. Для рассмотренных случаев получен ответ, возможно неверный из-за ошибок. | 1 |
| Все прочие случаи. | 0 |
| Максимальное количество баллов | 4 |
Аналоги к заданию № 484646: 484647 484648 511316 Все
Видео:ВСЁ ПРО ГРАФИКИ ЕГЭ 2024 (Прямая, Парабола, Окружность, Модуль, Гипербола, Корень, Области, Сдвиги)Скачать
Окружности помещены внутри параболы
Окружности w1, w2, w3, . помещены внутри параболы y = x 2 так, что w1 касается параболы в ее вершине и имеет радиус 0,5, окружность wт + 1 при каждом m касается окружности wm и ветвей параболы. Найти радиус окружности w2009.
Решение:
(№641 Математика 11, Л.А. Латотин, Б.Д. Чеботаревский)
Эту задачу можно решить, используя метод индукции.
Тогда уравнение окружности wт + 1 имеет вид:
Условие касания означает, что уравнение y + (y– (2Sn+ rn+1)) 2 = rn+1 2 имеет единственный корень, тогда его дискриминант:
Индукцией можно убедиться, что rn = n – 1/2.
.
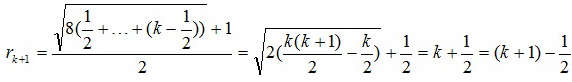
Значит, r2009 = 2009 – 1/2 = 2008,5.
Видео:А вы знали эти свойства параболы?Скачать
Задачи с параметрами. Условия касания.
Темы для повторения:
Графический метод решения задач с параметрами
Друзья, мы продолжаем тему «Задачи с параметрами». Это №18 Профильного ЕГЭ по математике. В этой статье рассказано, как в решении задач с параметрами применяется производная.
Рассмотрим следующую задачу:
При каких значениях параметра a уравнение имеет ровно 2 решения?
Поскольку логарифмы определены для положительных чисел, 
Это значит, что
Сделаем замену 
При 
каждому значению соответствует два значения
В левой части уравнения — линейная функция, в правой — логарифмическая. Это функции разных типов. Пытаться справиться с таким уравнение аналитически — бесполезно. Попробуем графический способ.
Если , то и условие не выполняется. Рассмотрим по отдельности случаи 
и 
Пусть . Нарисуем графики функций и Функция монотонно возрастает при . Обозначим 
Функция монотонно убывает при .
Докажем, что графики функций и имеют единственную точку пересечения при и любом 
Рассмотрим функцию Функция является монотонно возрастающей при 
(как сумма монотонно возрастающих функций и ), следовательно, каждое свое значение, в том числе и значение , она принимает ровно один раз.
Уравнение имеет единственное решение при положительных и Значит, при всех исходное уравнение имеет ровно 2 решения. Теперь случай
Уравнение имеет единственное решение, если прямая касается графика функции Мы помним, как записываются условия касания:
В нашем случае 
Учитывая, что , получим:
Мы получили, что, — точка касания. При этом .
Ответ: 
🔍 Видео
Урок 6. Параметры графический способ. Касание параболы и окружности Экстра ЕГЭСкачать
Парабола и окружностьСкачать
Параметр. Серия 13. Решение задач с окружностями. Касание двух окружностейСкачать
Параметр. Серия 14. Решение задач с окружностями. Касание окружности и гиперболыСкачать
КАК НАЙТИ ВЕРШИНУ ПАРАБОЛЫСкачать
Параметр. Серия 12. Решение задач с окружностями. Касание окружности и прямойСкачать
Всё о квадратичной функции. Парабола | Математика TutorOnlineСкачать
Всё про углы в окружности. Геометрия | МатематикаСкачать
Как расположится окружность если бросить её в параболу?Скачать
Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать
Математика без Ху!ни. Уравнение касательной.Скачать
5-часовой стрим по ПАРАМЕТРАМ. Вся ГРАФИКА для №17 с нуля и до уровня ЕГЭ 2023Скачать
✓ Как найти второй радиус? | Ботай со мной #105 | Борис ТрушинСкачать
✓ Параметры с нуля и до ЕГЭ | Задание 17. Профильный уровень | #ТрушинLive #041 | Борис ТрушинСкачать
10 класс, 43 урок, Уравнение касательной к графику функцииСкачать
Вся ГРАФИКА для параметров за 5 часов | №18 ЕГЭ 2024 по математикеСкачать
Параметры. Касание окружности и прямыхСкачать
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
