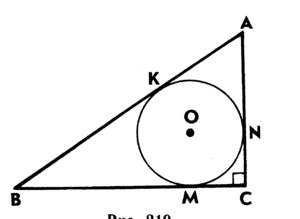
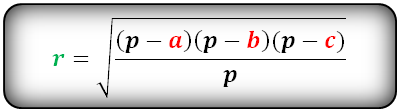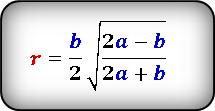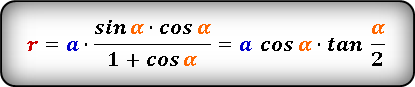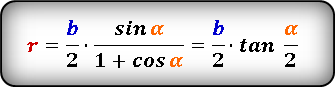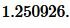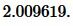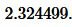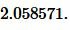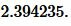- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- Радиус вписанной окружности в равнобедренный треугольник онлайн
- 1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
- 2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
- 3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
- 4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
- 5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
- Радиус окружности через периметр треугольник
- Все формулы для радиуса вписанной окружности
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в равносторонний треугольник
- Радиус вписанной окружности равнобедренный треугольник
- Радиус вписанной окружности в треугольник
- Радиус вписанной окружности в любой треугольник
- Радиус вписанной окружности в правильный треугольник
- Радиус вписанной окружности в равнобедренный треугольник
- Радиус вписанной окружности в прямоугольный треугольник
- Формула радиуса окружности, вписанной в треугольник
- Окружность, вписанная в треугольник
- Вычисление с помощью полупериметра
- Вычисление с учётом площади треугольника
- Расчёт с помощью тригонометрических функций
- Окружность, вписанная в прямоугольный треугольник
- Видео
- Видео
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

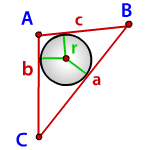
Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Видео:Формулы равностороннего треугольника #shortsСкачать

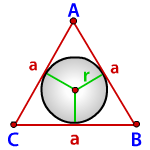
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
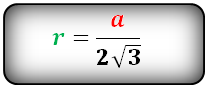
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Видео:Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

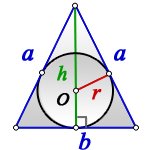
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
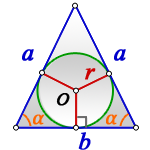
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Видео:Геометрия Найдите радиус окружности описанной около равнобедренного треугольника с основанием 16 смСкачать

Радиус вписанной окружности в равнобедренный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в треугольник окружности, в том числе радиус вписанной в равнобедренный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:Задача 6 №27934 ЕГЭ по математике. Урок 148Скачать

1. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и боковая сторона
Пусть известны известны основание a и боковая сторона b равнобедренного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной окружности через основание и боковую сторону.
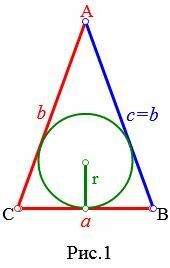 |
Радиус вписанной в треугольник окружности через три стороны a, b, c вычисляется из следующей формулы:
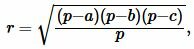 | (1) |
где полупериметр p вычисляется из формулы:
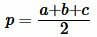 . . | (2) |
Учитывая, что у равнобедренного треугольника боковые стороны равны (( small b=c )), имеем:
| ( small p=frac ) ( small =frac, ) | (3) |
| ( small p-a=frac-a ) ( small =frac, ) | (4) |
| ( small p-b=p-c=frac-b ) ( small =frac. ) | (5) |
Подставляя (3)-(5) в (1), получим формулу вычисления радиуса вписанной в равнобедренный треугольник окружности:
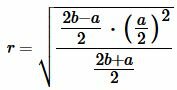 , , |
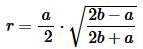 . . | (6) |
Пример 1. Известны основание a=13 и боковая сторона b=7 равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (6). Подставим значения ( small a,; b ) в (6):
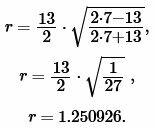 |
Ответ:
Видео:Вариант 55, № 8. Радиус окружности, описанной около равнобедренного треугольникаСкачать

2. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и угол при основании
Пусть известны основание a и прилежащий к ней угол β равнобедренного треугольника (Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
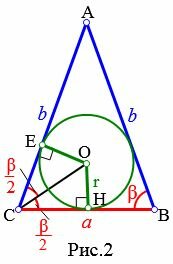 |
Из центра вписанной окружности проведем перпендикуляры OH и OE к сторонам a=BC и b=AC, соответственно (r=OH=OE). Соединим точки C и O. Полученные прямоугольные треугольники OCE и OCH равны по гипотенузе и катету (см. статью Прямоугольный треугольник. Тогда ( small angle OCE=angle OCH=frac. ) Для прямоугольного треугольника OCH можно записать:
| ( small frac=frac<large frac>=mathrmfrac .) |
Откуда получим формулу радиуса вписанной в треугольник окружности:
| ( small r=frac cdot mathrmfrac .) | (8) |
| ( small r=frac cdot frac .) | (9) |
Пример 2. Известны основание ( small a=15 ) и ( small beta=30° ) равнобедренного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанный в треугольник воспользуемся формулой (8) (или (9)). Подставим значения ( small a=15, ; beta=30° ) в (8):
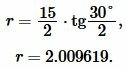 |
Ответ:
Видео:Периметр равнобедренного треугольникаСкачать

3. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и угол при основании
Пусть известны боковая сторона b и угол при основании β равнобедренного треугольника (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
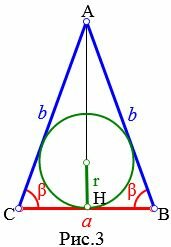 |
Высота равнобедренного треугольника AH делит равнобедренный треугольник ABC на две равные части. Тогда для треугольника AHC справедливо равенство:
| ( small frac=frac<large frac>= cos beta .) |
| ( small a=2b cdot cos beta .) | (10) |
Подставляя (10) в (8), получим формулу вписанной в равнобедренный треугольник окружности:
| ( small r=frac cdot mathrmfrac=frac cdot mathrmfrac ) ( small =b cos beta cdot mathrmfrac ) |
| ( small r=b cdot cos beta cdot mathrmfrac ) | (11) |
Учитывая формулы половинного угла тригонометрических функций, формулу (11) можно записать и так:
| ( small r=b cdot frac ) | (12) |
Пример 3. Известны боковая сторона равнобедренного треугольника: ( small b=9 ) и угол при основании β=35°. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11) (или (12)).
Подставим значения ( small b=9 ,; beta=35° ) в (11):
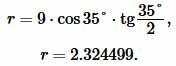 |
Ответ:
Видео:Свойство окружности, описанной около равнобедренного треугольникаСкачать

4. Радиус вписанной в равнобедренный треугольник окружности, если известны боковая сторона и высота
Пусть известны боковая сторона b и высота h равнобедренного треугольника (Рис.4). Найдем формулу радиуса вписанной в треугольник окружности.
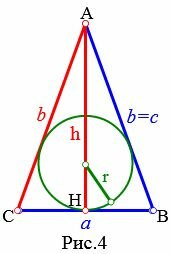 |
Формула радиуса вписанной окружности через площадь и полупериметр имеет следующий вид (см. статью на странице Радиус вписанной в треугольник окружности онлайн) :
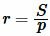 , , | (13) |
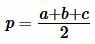 | (14) |
Так как треугольник AHC прямоугольный, то из Теоремы Пифагора имеем:
| ( small left( fracright)^2=b^2-h^2 ) |
| ( small a=2 cdot sqrt ) | (15) |
Площадь равнобедренного треугольника по основанию и высоте вычисляется из формулы:
| ( small S=frac cdot a cdot h. ) | (16) |
Подставим (15) в (16):
| ( small S=h cdot sqrt ) | (17) |
Учитывая, что для равнобедренного треугольника b=c, а также равенство (15), получим:
| ( small p=frac ) ( small =frac ) ( small =frac+b )( small =b+ sqrt ) | (18) |
Подставляя, наконец, (17) и (18) в (13), получим формулу радиуса вписанной в равнобедренный треугольник окружности:
| ( small r=frac ) ( small =frac<large h cdot sqrt><large b+ sqrt> ) | (19) |
Пример 4. Боковая сторона и высота равнобедренного треугольника равны ( small b=7 ,) ( small h=5, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (19). Подставим значения ( small b=7 ,) ( small h=5 ) в (19):
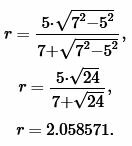 |
Ответ:
Видео:Периметр равнобедренного треугольника равен 250 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

5. Радиус вписанной в равнобедренный треугольник окружности, если известны основание и высота
Пусть известны основание a и высота h равнобедренного треугольника (Рис.5). Найдем формулу радиуса вписанной в равнобедренный треугольник окружности.
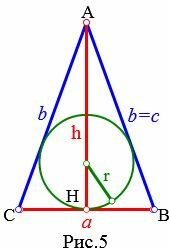 |
Из формулы (15) найдем b:
| ( small b^2-h^2=left( frac right)^2 ) |
| ( small b^2= frac +h^2 ) |
| ( small b= frac cdot sqrt) | (20) |
Подставляя (20) в (19), получим формулу радиуса вписанной окружности в равнобедренный треугольник:
| ( small r=frac<large h cdot sqrt><large b+ sqrt>) ( small =frac<large h cdot sqrt<frac+h^2-h^2>><large frac cdot sqrt+ sqrt<frac+h^2-h^2>>) ( small = large frac< h cdot frac>< frac cdot sqrt+frac >) |
| ( small r=large frac<a+ sqrt>) | (21) |
Пример 5. Основание и высота равнобедренного треугольника равны ( small a=7 ,) ( small h=9, ) соответственно. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в равнобедренный треугольник воспользуемся формулой (21). Подставим значения ( small a=7 ,) ( small h=9 ) в (21):
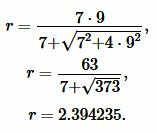 |
Ответ:
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

Радиус окружности через периметр треугольник
Видео:Периметр равнобедренного треугольника равен 240. ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Все формулы для радиуса вписанной окружности
Видео:Геометрия Периметр равнобедренного треугольника APK с основанием AP равен 32. Вписанная вСкачать

Радиус вписанной окружности в треугольник
a , b , c — стороны треугольника
p — полупериметр, p=( a + b + c )/2
Формула радиуса вписанной окружности в треугольник ( r ):
Видео:Равнобедренный треугольник. Свойства равнобедренного треугольника | Математика | TutorOnlineСкачать

Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
r — радиус вписанной окружности
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
Видео:Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать
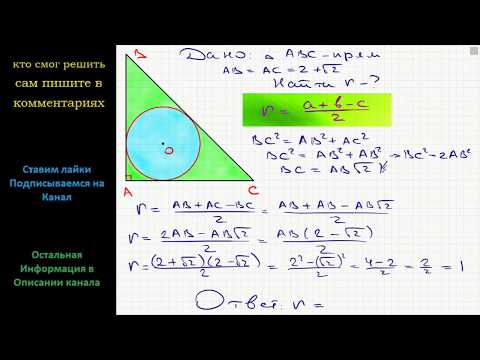
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
α — угол при основании
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
a — равные стороны равнобедренного треугольника
b — сторона ( основание)
h — высота
О — центр вписанной окружности
r — радиус вписанной окружности
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Видео:Высота равностороннего треугольника равна 13√3 ... | ОГЭ 2017 | ЗАДАНИЕ 9 | ШКОЛА ПИФАГОРАСкачать

Радиус вписанной окружности в треугольник
Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.
Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.
Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.
В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех
сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.
Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.
Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.
Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.
Всего различают четыре вида треугольников:
- Разносторонний / любой
- Правильный / равносторонний
- Равнобедренный / равнобочный
- Прямоугольный / прямой
Радиус вписанной окружности в любой треугольник
- Радиус вписанной окружности в любой треугольник через площадь и полупериметр
S — площадь; p — полупериметр;
Радиус вписанной окружности в любой треугольник через все стороны и полупериметр
a, b, c — стороны; p — полупериметр;
Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр
a — основание, сторона на которую падает высота; h — высота; p — полупериметр;
Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в правильный треугольник
- Радиус вписанной окружности в правильный треугольник через сторону
a — сторона;
Радиус вписанной окружности в правильный треугольник через радиус описанной окружности
R — радиус описанной окружности;
Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в равнобедренный треугольник
- Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание
a — боковая сторона; b — основание;
Радиус вписанной окружности в равнобедренный треугольник через высоту и основание
b — основание; h — высота;
Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Радиус вписанной окружности в прямоугольный треугольник
- Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу
a, b — катеты; с — гипотенуза.
Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета
c — гипотенуза; a, b — катеты;
Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности
D — диаметр вписанной окружности;
Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.
Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.
Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.
В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.
Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Формула радиуса окружности, вписанной в треугольник
Если окружность располагается внутри угла и касается его сторон, её называют вписанной в этот угол. Центр такой вписанной окружности располагается на биссектрисе этого угла.
Если же она лежит внутри выпуклого многоугольника и соприкасается со всеми его сторонами, она называется вписанной в выпуклый многоугольник.
Видео:Периметр равнобедренного треугольникаСкачать

Окружность, вписанная в треугольник
Окружность, вписанная в треугольник, соприкасается с каждой стороной этой фигуры лишь в одной точке. В один треугольник возможно вписать лишь одну окружность.
Радиус такой окружности будет зависеть от следующих параметров треугольника:
- Длин сторон треугольника.
- Его площади.
- Его периметра.
- Величины углов треугольника.
Для того чтобы вычислить радиус вписанной окружности в треугольник, не всегда обязательно знать все перечисленные выше параметры, поскольку они взаимосвязаны между собой через тригонометрические функции.
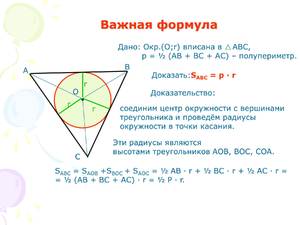
Вычисление с помощью полупериметра
Чтобы рассчитать величину радиуса вписанной окружности в треугольник, необходимо учитывать следующие параметры:
- Если известны длины всех сторон геометрической фигуры (обозначим их буквами a, b и c), то вычислять радиус придётся путём извлечения квадратного корня.
- Приступая к вычислениям, необходимо добавить к исходным данным ещё одну переменную — полупериметр (р). Его можно рассчитать, сложив все длины и полученную сумму разделив на 2. p = (a+b+c)/2. Таким образом можно существенно упростить формулу нахождения радиуса.
- В целом формула должна включать в себя знак радикала, под который помещается дробь, знаменателем этой дроби будет величина полупериметра р.
- Числителем данной дроби будет представлять собой произведение разностей (p-a)*(p-b)*(p-c)
- Таким образом, полный вид формулы будет представлен следующим образом: r = √(p-a)*(p-b)*(p-c)/p).
Вычисление с учётом площади треугольника
Если нам известна площадь треугольника и длины всех его сторон, это позволит найти радиус интересующей нас окружности, не прибегая к извлечению корней.
- Для начала нужно удвоить величину площади.
- Результат делится на сумму длин всех сторон. Тогда формула будет выглядеть следующим образом: r = 2*S/(a+b+c).
- Если воспользоваться величиной полупериметра, можно получить совсем простую формулу: r = S/p.
Расчёт с помощью тригонометрических функций
Если в условии задачи присутствует длина одной из сторон, величина противоположного угла и периметр, можно воспользоваться тригонометрической функцией — тангенсом. В этом случае формула расчёта будет иметь следующий вид:
r = (P /2- a)* tg (α/2), где r — искомый радиус, Р — периметр, а — значение длины одной из сторон, α — величина противоположного стороне, а угла.
Радиус окружности, которую необходимо будет вписывать в правильный треугольник, можно найти по формуле r = a*√3/6.
Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

Окружность, вписанная в прямоугольный треугольник
В прямоугольный треугольник можно вписать только одну окружность. Центр такой окружности одновременно служит точкой пересечения всех биссектрис. Эта геометрическая фигура имеет некоторые отличительные черты, которые необходимо учесть, вычисляя радиус вписанной окружности.
- Для начала необходимо выстроить прямоугольный треугольник с заданными параметрами. Построить такую фигуру можно по размеру её одной стороны и величинам двух углов или же по двум сторонам и углу между этими сторонами. Все эти параметры должны быть указаны в условии задачи. Треугольник обозначается как АВС, причём С — это вершина прямого угла. Катеты при этом обозначаются переменными, а и b, а гипотенуза — переменной с.
- Для построения классической формулы и вычисления радиуса окружности необходимо найти размеры всех сторон описанной в условии задачи фигуры и по ним вычислить полупериметр. Если в условиях даются размеры двух катетов, по ним можно вычислить величину гипотенузы, исходя из теоремы Пифагора.
- Если в условии дан размер одного катета и одного угла, необходимо понять, прилежащий этот угол или противолежащий. В первом случае гипотенуза находится с помощью теоремы синусов: с=a/sinСАВ, во втором случае применяют теорему косинусов с=a/cosCBA.
- Когда все расчёты выполнены и величины всех сторон известны, находят полупериметр по формуле, описанной выше.
- Зная величину полупериметра, можно найти радиус. Формула представляет собой дробь. Её числителем является произведение разностей полупериметра и каждой из сторон, а знаменателем —величина полупериметра.
Следует заметить, что числитель данной формулы является показателем площади. В этом случае формула нахождения радиуса гораздо упрощается — достаточно разделить площадь на полупериметр.
Определить площадь геометрической фигуры можно и в том случае, если известны оба катета. По сумме квадратов этих катетов находится гипотенуза, далее вычисляется полупериметр. Вычислить площадь можно, умножив друг на друга величины катетов и разделив полученное на 2.
Если в условиях даны длины и катетов и гипотенузы, определить радиус можно по очень простой формуле: для этого складываются длины катетов, из полученного числа вычитается длина гипотенузы. Результат необходимо разделить пополам.
Видео:Вписанная и описанная около равнобедренного треугольника, окружностьСкачать

Видео
Из этого видео вы узнаете, как находить радиус вписанной в треугольник окружности.
💡 Видео
№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать