Радикальная ось трех окружностей

Страницы работы

Фрагмент текста работы

Когда окружности пересекаются, то радикальная ось сливается с их общей хордой. Решая задачу № 71, можно убедиться, что радикальные оси трех окружностей встречаются в одной точке. Эта точка называется радикальным центром этих трех окружностей. Попьзуясь этим, легко определить радикальную ось двух окружностей. Именно, надо провести третью произвольную окружность, встречающую две данные окружности, и продолжить до встречи хорды пересечения; если сделать такое же построение в другой раз, то получим две точки, принадлежащие радикальной оси.

Радикальная ось имеет следующие замечательные свойства:

L Радикальная ось двух окружностей есть геометрическое место центров окружностей, встречающих данные окружности под прямым углом.

Пусть окружность О_л встречает данные окружности О, и О_а в точках А и В иод прямым углом. Тогда касательные 0$А и 0_%В раины, как радиусы, и потому точка 0_Л принадлежит радикальной оси окружностей О, и 0._г

IV. Радикальная ось двух окружностей расположена ближе к центру меньшей окружности.

1. Прямая, параллельная радикальной оси двух окружностей и проходящая в таком расстоянии от одного центра, в каком радикальная ось находится от другого центра, есть геометрическое место центров окружностей, пересекающих две данные окружности пополам.

Пусть окружность 0₃ встречает окружность О, по диаметру AB = 2R_> и другую данную окружность 0₃ по диаметру CD = 2R₂. Тогда 0₃0₃ а = /?_я й —/?₉» и 0_X0*=R₃ 2 —откуда 0₂0* — 0,0₃ а = = R* — /?_а*, между тем как всякая точка X радикальной оси окружностей О, и О.» должна удовлетворять равенству — O_sA’ 2 — — Rf 1 — Отсюда видно, чго точка 0₃ принадлежит прямой, проведенной перпендикулярно к 0,0₂ на таком расстоянии от 0_]( на каком радикальная ось проходит от

Самый легкий способ построения этого геометрического места основан на отыскании радикального центра данных и третьей произвольной окружности, встречающей две первые окружности.

XIV. Геометрическое место центров окружностей, имеющих данный радиус и пересекающих данную окружность под определенным углом, есть окружность, концентрическая данной окружности.

Если две окружности данных радиусов пересекаются иод данным углом, то хорда пересечения будет иметь определенную длину, и обратно. Поэтому, эту теорему можно выразить в такой форме:

Геометрическое место центров окружностей, имеющих данный радиус tf и пересекающих данную окружность по хорде данной длины а, есть концентрическая окружность. Построение этой окружности показано в № 72, П.

Примеры употребления метода геометрических мест:

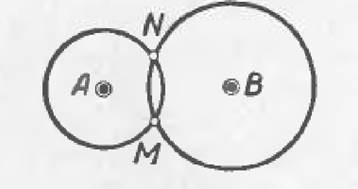
V. Найти точку, отстоящую от данной точки А на расстоянии, равном а, и от данной точки В на расстоянии> равном Ь.

Так как искомая точка отстоит or А (черт. 25) на расстоянии, равном а, то она лежит где-то на окружности, описанной из центра А радиусом, равным а

, так как н то же время расстояние искомой точки от точки В равно Ь, то она лежит на окружности, описанной из центра В радиусом, равным h. Искомая точка должна лежать и па той, и на другой окружности, след., она лежит в точке их пересечения. Значит, чтобы решить задачу, надо радиусами а а Ь описать окружности из центров А и В искомых точек вообще получим дне, М и N. Условие пересечения или касания окружностей будет условием возможности задачи: оно будет а + Ь-^АВ и Ь — а^АВ.

VII. 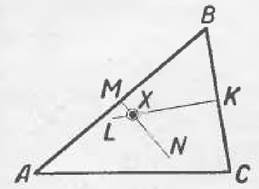Найти точку, равноотстоящую от всех трех вершин данного Д ABC (черт. 26),

Искомая точка отстоит от точек В и С па равном расстоянии, поэтому она есть одна нз точек перпендикуляра KL, восставленного из середины ВС. Подобным образом искомая точка есть одна из точек перпендикуляра MN, восставленного из середины АВ. Искомая точка лежит и на перпендикуляре AIN, и на перпендикуляре KL, значит, в их пересечении.

Поэтому, чтобы найти точку Л, на середин АВ и ВС восставляем перпендикуляры; в пересечение их будет искомая единственная точка. Доказательство предоставляем учащимся.

VIII. Найти тонну, находящуюся на расстоянии а от прямой А В и на расстоянии Ь от прямой CD (черт. 27).

Вели искомая точка находится на расстоянии а от АВ, то она лежит

Видео:Степень точки и радикальные оси | Олимпиадная математикаСкачать

Радикальная ось двух окружностей

Разделы: Математика

• углубить знания по темам «окружность» и «дополнительные построения», расширение математических познаний;
• совершенствовать навыки доказательств теорем;
• изучить метод решения геометрических задач с помощью свойств радикальной оси двух окружностей.

• развивать учебно-познавательную деятельность обучающихся;
• развивать логическое мышление и умения применять знания в нестандартных ситуациях.

3. Воспитательная: воспитывать аккуратность, культуру математической речи.

Оборудование: мел, доска, проектор.

Тип урока: изучение нового и первичное закрепления новых знаний.

1. Организационный момент – 2 мин.
2. Вступительное слово учителя – 1 мин.
3. Актуализация опорных знаний – 1 мин.
4. Формирование нового – 30 мин.
5. Первичное закрепление – 10 мин.
6. Рефлексия – 1 мин.

1. Организационный момент. Приветствие.

2. Вступительное слово.

Если отслеживать историю достижений учащихся на математических соревнованиях, то можно не раз заметить такую картину: до 9 класса ученик очень успешно выступает на различных олимпиадах, однако почему то в 10 классе его результаты сильно понижаются. Трудно полностью объяснить причину подобного, однако, несомненно, что это отчасти связано с существенным различием в уровне задач 9 и 10 классов. Непосвященному это трудно заметить. Например, остановимся геометрических задачах, связанных с окружностью. В большинстве случаев такие задачи можно решить методами 9 классов, однако, такое решение будет слишком громоздким и отнимет много времени на оформление, что в виду ограниченности времени на олимпиадах далеко не всегда осуществимо. Поэтому изучение методов 10 класса для решения задач является жизненной необходимостью для успешного участия на олимпиадах, хотя в истории бывали и исключения, когда некоторые умудрялись решить сложную задачу 10 класса методами 9 класса.

3. Актуализация опорных знаний.

Традиционно на олимпиадах есть хотя бы одна геометрическая задача, а среди таких задач наибольшую трудность вызывают задачи связанные с окружностями. Несмотря на то, что не существует общего метода решения всех геометрических задач, связанных с окружностью, для решения достаточно большого класса таких задач оказываются полезным свойства радикальной оси, поляр, полюсов и некоторых элементов проективной геометрии. Сегодня мы начнем изучение некоторых первичных свойств радикальной оси, однако даже эти свойства могут быть полезны для решения сложных геометрических задач, которые встречаются на международных олимпиадах. Также мы разберем решения нескольких задач российских геометрических олимпиад, заслуженно признанных одними из самых сложных по геометрии.

4. Формирование нового.

Определение 1 (см. [1], стр. 122). Пусть дана окружность ω с центром в точке О и радиусом R. Степенью точки М относительно окружности ω называется число ОМ 2 – R 2 .

Определение 2 (см. [1], стр. 122). Пусть даны две окружности ω₁ и ω₂. Радикальной осью двух окружностей называется множество всех точек плоскости, каждая из которых имеет равные степени относительно этих окружностей.

Теорема 1. Пусть даны две окружности ω₁ и ω₂, центры которых различны. Тогда для этих окружностей радикальная ось существует и является прямой линией.

1. Если две окружности ω₁ и ω₂ пересекаются в двух различных точках, то радикальная осью этих окружностей является прямая проходящая через точки их пересечения.
2. Если две окружности ω₁ и ω₂ касаются внешним или внутренним образом, то их радикальная ось совпадает с общей касательной в точке касания окружностей.
3. Если две окружности ω₁ и ω₂ лежат одна вне другой, не касаясь, то радикальная ось содержит середины общих касательных этих окружностей.

Доказательство. Вне зависимости от того как пересекаются окружности согласно теореме о том, что разность квадратов наклонных, проведенных из одной точки, равна разности квадратов из проекций на прямую, геометрическим местом точек, имеющих одинаковые степени относительно двух заданных окружностей, является прямая, перпендикулярная линии центров окружностей. Для того, чтобы однозначно знать положение прямой достаточно знать две ее точки.

I	I I	I I I

В первом случае, когда окружности пересекаются в двух точках, эти точки будут иметь равные степени относительно них, равные нулю, поэтому радикальной осью для таких окружностей будет прямая, проходящая через точки пересечения окружностей.

Во втором случае, когда окружность каются внешним или внутренним образом, также общая точка окружностей будет иметь одинаковые степени относительно них, значит, в этом случае радикальной осью будет прямая, проходящая через точку касания окружностей и перпендикулярная их линии центром.

В третьем случае, радикальная ось будет проходить через середины отрезков общих касательных, поскольку степенью точки этих точки является квадрат отрезка касательной, проведенной из точки к окружности.

Замечание 1. Теорема 1 применима и в случае, если радиус одной из окружностей равен нулю.

Пример 1 (см. [2], стр. 64, задача №3.65). На окружности S с диаметром AB взята точка C, из точки C опущен перпендикуляр CH на прямую AB. Докажите, что общая хорда окружности S и окружности S₁ с центром C и радиусом CH делит отрезок CH пополам.

Решение (см. [2], стр. 76). Пусть M – середина отрезка CH. Докажем, что точка M лежит на радикальной оси окружностей S и S₁, т.е. её степени относительно этих окружностей равны. Пусть радиусы окружностей S и S₁ равны 2R и 2r.

Тогда степень точки M относительно окружности S₁ равна CM 2 – 4r 2 = -3r 2 , а её степень относительно S равна OM 2 – 4R 2 , где O – середина отрезка AB. Ясно, что OH 2 = 4R 2 – 4r 2 , поэтому OM 2 = 4R 2 – 4r 2 + r 2 = 4R 2 – 3r 2 . Следовательно, OM 2 – 4R 2 = -3r 2 . Таким образом, точка М лежит на ED, следовательно, ED делит CH пополам.

Теорема 2 (см. [1], стр.125). Если центры трех окружностей неколлинеарные, то три радикальные оси этих окружностей, взятых попарно, имеют общую точку.

Доказательство. Пусть даны три окружности Ω₁, Ω₂, Ω₃, центры которых неколлинеарные.

Поскольку центры трех окружностей неколлинеарные, то прямые перпендикулярные O₁O₂ и O₁O₃ пересекаются, значит, не параллельны и радикальные оси к Ω₁ и Ω₂, а также к Ω₁ и Ω₃ пересекаются в некоторой точке, которую обозначим буквой Е. Отсюда, степени точки Е относительно Ω₁ и Ω₂ равны, и относительно Ω₁ и Ω₃ тоже равны. Следовательно, точки Е имеет одинаковые степени относительно Ω₂ и Ω₃, а это означает, что она лежит на радикальной оси к окружностям Ω₂ и Ω₃, т.е. все три радикальные оси пересекаются в одной точке. Что и требовалось доказать.

Пример 2 (Турнир городов, весенний тур, базовый вариант, 10-11 класс, 2012 г.). Четырехугольник ABCD без параллельных сторон вписан в окружность. Для каждой пары касающихся окружностей, одна из которых имеет хорду AB, а другая – хорду CD, отметим их точку касания X. Докажите, что все такие точки X лежат на одной окружности.

Решение (см. [3]). обозначим через Ω₁ и Ω₂ касающиеся окружности, содержащие соответственно хорды AB и СD, а через Ω – описанную окружность четырехугольника ABCD. Пусть O – точка пересечения прямых AB и СD.

Тогда согласно теореме 1 прямая AB – радикальная ось окружностей Ω₁ и Ω, CD – радикальная ось окружностей Ω₂ и Ω, а общая касательная окружностей Ω₁ и Ω₂ – их радикальная ось. Согласно теореме 2 эти три радикальные оси пересекаются в одной точке, которую обозначим буквой O.

При этом квадрат длина касательной OX равна степени точки O относительно Ω₁, то есть OA× OB, значит, что точка X лежит на окружности с центром О и радиусом .

Пример 3 (Московская устная олимпиада по геометрии, 8-9 класс, 2005). Дан шестиугольник ABCDEF, в котором AB = BC, CD = DE, EF = FA, а углы A и C – прямые. Докажите, что прямые FD и BE перпендикулярны.

Решение №1 (см. [3]). Поскольку по теореме Пифагора

BD 2 + EF 2 = BC 2 + CD 2 + EF 2 = AB 2 + DE 2 + AF 2 = BF 2 + DE 2 , то согласно критерию перпендикулярности диагоналей выпуклого четырехугольника FD и BE перпендикулярны.

Решение №2 (см. [3]). Рассмотрим окружности с центрами D и F и радиусами DC и EF соответственно. Тогда BA = BC – касательные к этим окружностям, а точка E принадлежит обеим окружностям, поэтому BE – их радикальная ось, и следовательно, она перпендикулярна линии центров FD.

5. Первичное закрепление.

(Всероссийская олимпиада по математике, 10 класс, 2011 г.) Периметр треугольника ABC равен 4. На лучах AB и AC отмечены точки X и Y так, что AX = AY = 1. Отрезки BC и XY пересекаются в точке M. Докажите, что периметр одного из треугольников ABM и ACM равен 2.

(Московская устная олимпиада по геометрии, 10-11 класс, 2011 г.) Дана неравнобокая трапеция ABCD (AB ǁ CD). Произвольная окружность, проходящая через точки A и B, пересекает боковые стороны трапеции в точках P и Q, а диагонали – в точках M и N. Докажите, что прямые PQ, MN и CD пересекаются в одной точке.

(Всероссийская олимпиада по математике, 11 класс, 2005 г.) Пусть AA₁ и BB₁ – высоты остроугольного неравнобедренного треугольника ABC. Известно, что отрезок A₁B₁ пересекает среднюю линию, параллельную AB, в точке C’. Докажите, что отрезок CC’ перпендикулярен прямой, проходящей через точку пересечения высот и центр описанной окружности треугольника ABC.

— Что особенно сегодня вам запомнилось?

— Полезно ли для решения некоторых геометрических задач знать свойства радикальной оси двух окружностей?

Видео:Степень точки. Радикальная ось. Радикальный центр.Скачать

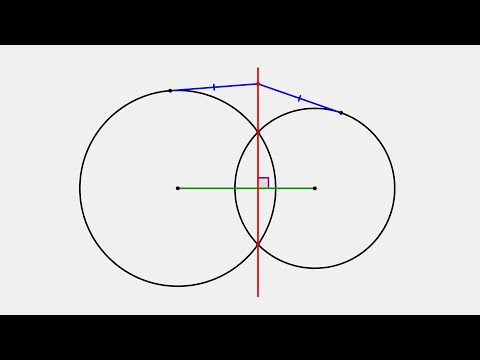
Радикальная ось.

Определение. Радикальная ось двух не концентрических окружностей — геометрическое место точек, имеющих равные степени относительно этих окружностей.

Теорема. Если две окружности не концентрические, то их радикальная ось существует и является прямой, перпендикулярной линии, проходящей через центры этих окружностей.

Утверждение 1. Если степени точки относительно двух окружностей равны, то равны отрезки касательных, проведенные из нее к этим окружностям.

Утверждение 2. Если к двум окружностям проведены две внешние и две внутренние касательные, то середины отрезков, соединяющих точки касания, лежат на одной прямой.

Утверждение 3. Общая касательная двух окружностей делится их радикальной осью пополам.

Утверждение 4. Радикальная ось двух пересекающихся окружностей проходит через точки их пересечения.

Утверждение 5. Радикальная ось двух касающихся окружностей есть их общая касательная, проведённая в точке касания.

Утверждение 6. Радикальная ось двух непересекающихся окружностей не пересекает ни одну из них.

Теорема. Три прямые, являющиеся радикальными осями пар трех не концентрических окружностей пересекаются в одной точке или параллельны или совпадают. Если центры окружностей лежат на одной прямой, то их радикальные оси перпендикулярны этой прямой, то есть параллельны или совпадают. Если центры окружностей не лежат на одной прямой, то их радикальные оси пересекаются в одной точке.

Определение. Для трех окружностей, центры которых не лежат на одной прямой, точка, для которой ее степени относительно всех трех окружностей равны, называется радикальным центром трех окружностей.

📹 Видео

Радикальные оси для ЕГЭ профиль. Геометрические конструкции, убивающие №16Скачать

Касание окружностей, радикальная ось, лемма Архимеда. (Геометрические конструкции)Скачать

Степень точки, радикальная ось. Планиметрия из ВСОШ и Высшей пробы. Чтобы решать планиметрию нужно..Скачать

М630. Радикальная ось окружности и точкиСкачать

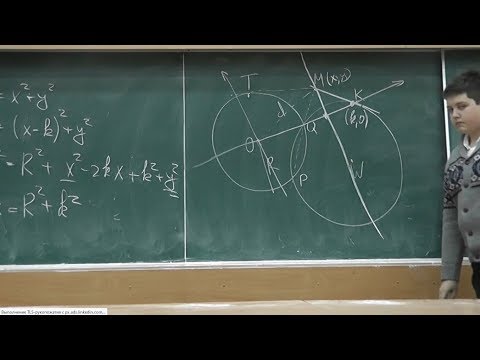
Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 3Скачать

Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 1Скачать

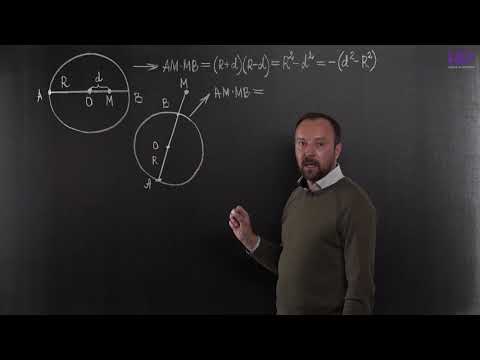
Математика. ПЕРЕЧНЕВЫЕ ОЛИМПИАДЫ. Степень точки. Радикальные осиСкачать

Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 2Скачать

Трапеция и три радикальные оси | Готовимся ко ВсероссуСкачать

Радикальная ось. IntroСкачать

Геометрия, 10 класс | Степень точки относительно окружности. Радикальная ось. Часть 4Скачать

#1 Степень точки и радикальные оси - секретный приём из геометрии!Скачать

Радианная Мера Угла - Как Переводить Градусы в Радианы // Урок Алгебры 10 классСкачать

10 класс, 11 урок, Числовая окружностьСкачать

Тригонометрическая окружность. Как выучить?Скачать

04 71196 Степень точкиСкачать

ЕГЭ Задание 16 Комбинация трёх окружностейСкачать