Прямые аб и сд параллельные аб перпендикулярна

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Ваш ответ

Видео:Перпендикулярные прямые. 6 класс.Скачать

Похожие вопросы

• Все категории
• экономические 43,277
• гуманитарные 33,618
• юридические 17,900
• школьный раздел 606,658
• разное 16,822

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.

Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.

Видео:№44. Прямые ОВ и CD параллельные, а ОА и CD — скрещивающиеся прямые.Скачать

Урок геометрии по теме «Перпендикулярность прямой и плоскости». 10-й класс

Разделы: Математика

Класс: 10

Цели:

1. закрепить вопросы теории по теме «Перпендикулярность прямой и плоскости»;
2. вырабатывать навыки применения теоретических знаний к решению типовых задач на перпендикулярность прямой и плоскости.

План:

1. Теоретический опрос.
   1. Доказательство изученных теорем у доски.
   2. Фронтальный опрос.
   3. Презентации учащихся по данной теме.
2. Решение задач.
   1. Решение устных задач по готовым чертежам.
   2. Решение письменных задач (по группам).
   3. Самостоятельная работа с индивидуальным заданием.
3. Итог урока. Задание на дом.

Ход урока

I. Теоретический опрос (4 ученика у доски)

1) доказать лемму о 2-ух параллельных прямых, одна из которых перпендикулярна к третьей;
2) доказать теорему о 2-ух параллельных прямых, одна из которых перпендикулярна к плоскости;
3) доказать обратную теорему о параллельности 2-ух прямых, перпендикулярных к плоскости;
4) доказать признак перпендикулярности прямой и плоскости.

Пока ученики готовятся у доски к ответу, с классом проводится фронтальный опрос.
(С помощью мультимедиапроектора на экране появляются вопросы (Приложение 1), и ученики отвечают на них)

1. Закончить предложение:

а) две прямые в пространстве называются перпендикулярными, если… (угол между ними равен 90°)
б) прямая называется перпендикулярной к плоскости, если… (она перпендикулярна к любой прямой, лежащей в этой плоскости)
в) если две прямые перпендикулярны к плоскости, то они… (параллельны)
г) если плоскость перпендикулярна к одной из двух параллельных прямых, то она… (перпендикулярна и к другой прямой)
д) если две плоскости перпендикулярны к одной прямой, то они… (параллельны)

2. Дан параллелепипед

б) Определите взаимное расположение:
1) прямой CC₁ и плоскости (DСВ) (ответ: они перпендикулярны)
2) прямой D₁C₁ и плоскости (DCB) (ответ: они параллельны)

Далее выслушиваются ответы учеников у доски с дополнениями и исправлениями по необходимости. Затем рассматриваются презентации по данной теме, подготовленные рядом учеников в качестве зачётных работ (Приложение 2, Приложение 3, Приложение 4).
(Накануне изучения каждой темы учащимся предлагается такой вариант зачёта)

II. Решение задач.

1. Решение задач по готовым чертежам (Устно)

№1

Дано: ∆ ABC — прямоугольный; AM ⊥ AC; M ∉ (ABC)
Доказать: AC ⊥ (AMB)
Доказательство: Т.к. AC ⊥ AB и AC ⊥ AM, а AM ⋂ AB, т.е. АМ и АВ лежат в плоскости (АМВ), то AC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

№2

Дано: ВМDC — прямоугольник, M ∉ (ABC), MB ⊥ AB
Доказать: CD ⊥ (ABC)
Доказательство: MB ⊥ BC, т.к. ВМDC – прямоугольник, MB ⊥ AB по условию, BC ⋂ AB, т.е. ВС и АВ лежат в плоскости (АВС) ⇒ MB ⊥ (ABC) по признаку перпендикулярности прямой и плоскости. СD ∥ МВ по свойству сторон прямоугольника ⇒ CD ⊥ (ABC) по теореме о двух параллельных прямых, одна из которых перпендикулярна к плоскости (то и другая прямая перпендикулярна к этой плоскости).
Ч.т.д.

№3

Дано: АВСD – прямоугольник, M ∉ (ABC), MB ⊥ BC
Доказать: AD ⊥ AM
Доказательство:
1) ∠ABC = 90°, т.к. АВСD – прямоугольник ⇒ BC ⊥ AB, BS ⊥ MB по условию, MB ⋂ AB = B, т.е. МВ и АВ лежат в плоскости (АМВ) ⇒ BC ⊥ (AMB) по признаку перпендикулярности прямой и плоскости.
2) BC ∥ AD (по свойству сторон прямоугольника) ⇒ AD ⊥ (AMB) по теореме о двух параллельных прямых, одна из которых перпендикулярна плоскости (то и другая прямая перпендикулярна к этой плоскости).
3) Т.к. AD ⊥ (AMB) ⇒ AD ⊥ AM по определению прямой, перпендикулярной плоскости.
Ч.т.д.

№4

Дано: АВСD – параллелограмм, M ∉ (ABC), МВ = МD, МА = МС
Доказать: MO ⊥ (ABC)
Доказательство:
1) Т.к. О – точка пересечения диагоналей параллелограмма, то АО = СО и ВО = DO. ∆ BMD — равнобедренный, т. к. ВМ = МD по условию, значит МО — медиана и высота, т.е. MO ⊥ BD.
2) Аналогично доказывается в ∆ AMC: MO ⊥ AC.
3) Итак, MO ⊥ BD и MO ⊥ AC. а ВD и АС – пересекающиеся прямые, лежащие в плоскости (АВС) ⇒ MO ⊥ (ABC) по признаку перпендикулярности прямой и плоскости.
Ч.т.д.

(Устные ответы к каждой задаче требуется обосновывать, проговаривая всякий раз формулировки применяемых теорем)

2. Решение письменных задач

Класс делится на три группы (например, по рядам), и каждой группе даётся задача с последующей проверкой решения у доски.

№1.2 (№125 учебника)

Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P₁ и Q₁. Найдите P₁Q₁, если PQ = 15 cм; PP₁ = 21,5 cм; QQ₁ = 33,5 cм.
Решение:

1) PP₁ ⊥ α и QQ₁ ⊥ α по условию ⇒ PP₁ ∥ QQ₁ (обосновать);
2) PP₁ и QQ₁ определяют некоторую плоскость β, α ⋂ β = P₁Q₁;
3) PP₁Q₁Q — трапеция с основаниями PP₁ и QQ₁, проведём PK ∥ P₁Q₁;
4) QK = 33,5 — 21,5 = 12 (см)

P1Q1 = PK =

= 9 см.

№2.2

1) ∆ ABD: ∠BAD = 90°; АD = BC = 8 см;

ВD =

см;

2) ∆ DD₁B: ∠D₁DB = 90°;

DD1 =

= 12 см;

3) SBB1D1D = BD ∙ DD1 =

см 2 .

Ответ:

см 2 .

№3.2

Отрезок МН пересекает плоскость α в точке К. Из концов отрезка проведены прямые МЕ и НР, перпендикулярные к плоскости α. НР = 4 см; МЕ = 12 см; НК = 5 см. Найдите отрезок РЕ.
Решение:

1) Т.к. прямые МЕ и НР перпендикулярны к плоскости α, то МЕ ∥ НР (обосновать) и через них проходит некоторая плоскость β. α ⋂ β = EP;
2)МЕ ⊥ EP; НР ⊥ EP(обосновать), т.е. ∠MEK = ∠HPK = 90°;

3) ∆ HPK: KP =

= 3 см;

4) ∠EMK = ∠PHK (накрест лежащие для параллельных прямых МЕ и НР и секущей МН),

тогда ∆ MEK ∆ HPK по двум углам и

; т.е.

⇒ EK =

= 9 см,

РЕ = РК + КЕ, РЕ = 3 + 9 = 12 см.

Ответ: РЕ = 12 см.

3. Самостоятельная работа (направлена на проверку усвоения материала по данной теме)

1) AA₁ ⊥ AB, AA₁ ⊥ AD, а AB ⋂ AD = A ⇒ AA₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. AA₁ ∥ BB₁, то BB₁ ⊥ (ABC) ⇒ BB₁ ⊥ BD;
2) ∆ ABD: ∠BAD = 90°. По теореме Пифагора:

BD =

= 20 см;

3) ∆ B₁BD – прямоугольный. По теореме Пифагора:

B1B =

= 15 см.

1) BB₁ ⊥ AB, BB₁ ⊥ BC, а AB ⋂ BC = B ⇒ BB₁ ⋂ (ABC) (по признаку перпендикулярности прямой и плоскости), а т.к. BB₁ ∥ AA₁, то AA₁ ⊥ (ABC) ⇒ AA₁ ⊥ AC;
2) Используя свойство диагоналей ромба, имеем в ∆ AOB: ∠AOB = 90°, BO = ½ BD = 8 см. По теореме Пифагора:

AO =

= 6 см,

AO = ½ AC ⇒ AC = 12 см;
3) ∆ A₁AC – прямоугольный. По теореме Пифагора:

AA1 =

= 5 см.

Индивидуальное задание для более сильных учеников. (Вариант III)

1) Т.к. CD ⊥ (FDC) ⇒ CD ⊥ AC и CD ⊥ BC, т.е. ∆ ADC, ∆ BDC – прямоугольные;
2) ∆ ADC = ∆ BDC (по двум катетам) ⇒ AD = BD, т.е. ∆ ADB – равнобедренный и DM – медиана, а значит и высота; 3) DC ⊥ MC ⇒ MCD – прямоугольный,

тогда MC =

= 9;

4) ∆ ABC – равносторонний, поэтому СМ – медиана и высота, т.е. ∆ MCB – прямоугольный, ∠B = 60°,

sin ∠B =

, тогда

,

а АВ = ВС (по условию).
5) S_{∆ ADB} = ½ DM ∙ AB;

S∆ ADB = ½ ∙ 15 ∙

.

Ответ:

III. Подводятся итоги урока. Задание на дом: повторить теоретический материал по изученной теме, глава II, №130, №131.

Для подготовки к уроку использовались материалы учебника «Геометрия – 10-11» авторов Л.С. Атанасяна, В.Ф. Бутузова и др., методические рекомендации к учебнику «Изучение геометрии в 10-11 классах» авторов С.М. Саакяна, В.Ф. Бутузова, «Поурочные разработки по геометрии» автора В.А. Яровенко.

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Прямые AB и CD параллельны, а прямые EF и AB перпендикулярны?

Математика | 1 — 4 классы

Прямые AB и CD параллельны, а прямые EF и AB перпендикулярны.

Укажите верное утверждение.

1)прямые AB и CD не пересекаются

2)прямые AB и CD пересекаются

1)они не пересекаются.

Только а, так как параллельные прямые никогда не пересекаются.

Видео:№215. Параллельные прямые АВ и CD лежат в разных гранях двугранного угла, равного 60°. Точки А и DСкачать

Выберете неверное утверждение?

Выберете неверное утверждение.

А)если при пересечении двух прямых секущей сумма внутренних односторонних углов равна 180 * , то эти прямые параллельны.

Б)Если две прямые перпендикулярны третьей прямой, то они не параллельны между собой.

В)В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданную прямой.

Г)Если некая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую параллельную прямую.

Видео:Параллельные прямые. 6 класс.Скачать

14. Отметьте верные утверждения?

14. Отметьте верные утверждения.

A) Если прямая перпендикулярна к одной из двух прямых, то она перпендикулярна и к другой.

B) Через точку, не лежащую на данной прямой, проходит несколько прямых, параллельных данной.

C) Если две прямые параллельны третьей прямой, то они параллельны.

D) все утверждения верны.

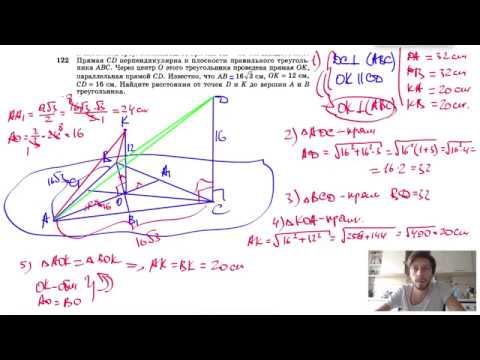
Видео:№122. Прямая CD перпендикулярна к плоскости правильного треугольника ABC. Через центр О этогоСкачать

Какие прямые называются пересекающимися, параллельными, перпендикулярными?

Какие прямые называются пересекающимися, параллельными, перпендикулярными?

Видео:№198. Прямые а и b перпендикулярны к прямой р, прямая с пересекает прямую а. ПересекаетСкачать

Верно ли утверждение : если две прямые не имеют общих точек, то они параллельны?

Верно ли утверждение : если две прямые не имеют общих точек, то они параллельны?

Видео:10 класс, 16 урок, Параллельные прямые, перпендикулярные к плоскостиСкачать

Верно ли утверждение : если две прямые параллельны не которой плоскости, то они параллельны друг другу?

Верно ли утверждение : если две прямые параллельны не которой плоскости, то они параллельны друг другу?

Видео:10 класс, 15 урок, Перпендикулярные прямые в пространствеСкачать

Помогите пж?

Указать следствия аксиомы параллельных прямых :

а) Если отрезок или луч пересекает одну из параллельных прямых, то он пересекает и другую.

Б) Если две прямые параллельны третьей прямой, то они параллельны друг другу.

В) Если прямая пересекает одну из параллельных прямых, то она пересекает и другую.

Г) Если три прямые параллельны, то любые две из них параллельны друг другу.

Д)если две прямые не параллельны третьей прямой, то они не парральны между собой.

Е) если прямая пересекает одну из параллельных прямых, то она не может не пересекать другую.

Ж) если две прямые параллельны третьей прямой, то они не могут быть не параллельны между собой.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Прямые а и в параллельны?

Прямые а и в параллельны.

Прямая с пересекает прямую а .

Пересекает ли прямая с прямую в ?

Если пересекает, то почему?

Видео:7 класс, 30 урок, Углы с соответственно параллельными или перпендикулярными сторонамиСкачать

Какое из утверждений неверно?

Какое из утверждений неверно?

А)На плоскости две прямые, перпендикулярные третьей прямой, параллельны.

Б)Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.

В)На плоскости две прямые, перпендикулярные третьей прямой, пересекаются.

Г)На плоскости две прямые, параллельные третьей прямой, параллельны.

Видео:Параллельные прямые (задачи).Скачать

Любые две прямые на плоскости пересекаются?

Любые две прямые на плоскости пересекаются.

Это верное утверждение?

Видео:10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Плачу 31 балл?

Ответьте, верны ли утверждения :

Две прямые параллельный одной и той же прямой не пересекаются

У любого четырехугольника есть перпендикулярные стороны

Параллельные прямые не имеют ни одной общей точки

Если прямая параллельна одной из двух перпендикулярных прямых, то она параллельна и второй

Через каждую точку плоскости можно провести одну прямую, перпендикулярную данной прямой.

На странице вопроса Прямые AB и CD параллельны, а прямые EF и AB перпендикулярны? из категории Математика вы найдете ответ для уровня учащихся 1 — 4 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

1)x ^ 2 — 2x = 10x — 36 x ^ 2 — 12x + 36 = 0 D = b ^ 2 — 4ac = 144 — 144 = 0 x = — b / 2a = — ( — 12) / 2 = 6 Ответ : 6 2)4y / y — 4 — — 4y(находим наименьший общий знаминатель y — 4 и умножаем 4у на у — 4) = (4y ^ 2 — 4y ^ — 16y) / y — 4 = — 16y / y..

(4. 2 / х) / 1. 2 = 3 4. 2 / х = 3 * 1, 2 4, 2 / х = 3, 6 х = 4. 2 / 3, 6 х = 1 1 / 6 Ответ : .

На таблицу умножения просто посмотри.

1) звенья равны ( если честно, то по твоей фотке непонятно , т. К. она выполнена наискосок) 2) с помощью линейки с помощью циркуля : прикоажываешь одну ножку циркуля в началу отрезка, другую — к его концу . И сравниваешь можно опустить перпендикуля..

160 + 60% = 256(км) — весь путь.

160 оставшийся путь равен 40 % 160 — 40% х — 100% х = 160 * 100 / 40 х = 400.

С четными — 20, 22, 24, 26, 28, 40, 42, 44, 46, 48, 60, 62, 64, 66, 68, 80, 82, 84, 86, 88. 20 чиселс нечетными — 11, 13, 15, 17, 19, 31, 33, 35, 37, 39, 51, 53, 55, 57, 59, 71, 73, 75, 77, 79, 91, 93, 95, 97, 99. 25 чисел.

📺 Видео

Перпендикулярные прямыеСкачать

Наклонная, проекция, перпендикуляр. 7 класс.Скачать

SOS-ГЕОМЕТРИЯ! Отрезки и углы, смежные и вертикальные углы | Математика TutorOnlineСкачать

Параллельные и перпендикулярные прямые.Скачать

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

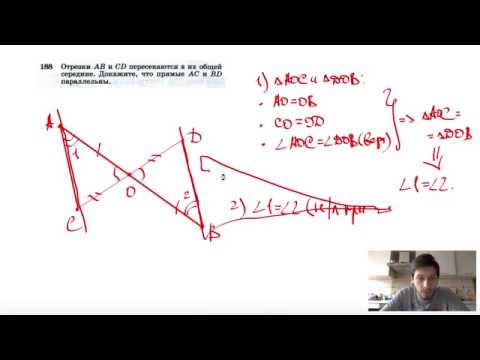
№188. Отрезки АВ и CD пересекаются в их общей середине. Докажите, что прямые АССкачать