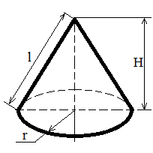
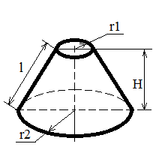
Прямой круговой конус пересечен плоскостью параллельной основанию на расстоянии 3 см от вершины (7 видео)

Конус пересечена плоскостью, параллельной базе, на расстоянии 3 см от вершины.

Конус пересечена плоскостью, параллельной базе, на расстоянии 3 см от верхушки. Отыскать площю основания конуса, если площадь сечения 16П см, а вышина конуса 9 см.

Полина Мяч
Геометрия 2019-06-04 19:53:15 0 1

Осмотрим осевое сечение конуса.Верхний треугольник сходственен большому с коэффициентом к=9:3=3.Плоскость сечения (круг) сходственна плоскости основания с к=3. Площади сходственных фигур относятся как квадрат коэффициента подобия, т.е. 9. Площадь основания одинакова 16П*9=144П.

Содержание

Круглые тела. КОНУС
Просмотр содержимого документа «Круглые тела. КОНУС»
Решение задач на нахождение объема конуса — Объем наклонной призмы, пирамиды и конуса — ОБЪЕМЫ ТЕЛ
🌟 Видео

Видео:Усеченный конус. 11 класс.Скачать

Круглые тела. КОНУС

Практическая работа по теме: «КОНУС» (решение задач)

Просмотр содержимого документа
«Круглые тела. КОНУС»

Инструкционная карта № 30

Тақырыбы/ Тема: Решение задач по теме: «Конус».

1. Проверить теоретическую часть знаний учащихся по определению понятия конуса, видов конусов, свойства конуса, определение площади поверхности конуса.

2. Воспитание познавательной самостоятельности: развитие умения самостоятельно планировать, выполнять анализ, оценивать результаты.

3. Создать условие для развития коммутативно-творческих умений: не шаблонно подходить решению разнообразных задач.

S_бок = π r l, где l – образующая конуса
S_кон = π r (r+l);
V = 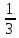π r 2 H

Связь между r, l , H: r 2 = l 2 — H 2

S_бок = π l (r₁ + r₂);
V = 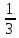π H (r₁ 2 + r₂ 2 + r₁ r₂)

Площади оснований усеченного конуса 4 дм 2 и 16 дм 2 . Через середину высоты проведена плоскость, параллельная основаниям. Найдите площадь сечения.

Дано: усеченный конус

S_сеч=R 2 =O₂A₂ 2 S_o=R 2 R 2 =16/ R=4/

S_o1=r 2 r 2 =4/ r=2/

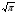
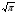
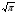
Рассм. О₁А₁АО-трапеция, О₂А₂-средняя линия трапеции, О₂А₂=1/2(О₁А₁+ОА)=1/2(4/+2/)=1/2*6/=3/

S_сеч=*9/=9( дм 2 ).

Конус пересечен плоскостью, параллельной основанию, на расстоянии d от вершины. Найдите площадь сечения, если радиус основания конуса R, а высота Н.

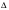
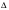
Рассм.SOA и SO₁A₁

1) S-общий;

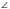
2) A₁=A; SOA подобен SO₁A₁

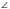
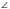
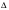
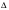
= = O₁A₁= =r Sсеч= =

3. Образующая конуса равна 6 м, | L=6 =60 0 S_осн=R 2

а угол между нею и плоскостью | R=Lcos60 0 =6*0,5=3

основания равен 60 0 . Найдите | S_осн=3 2 =9 (см 2 )

площадь основания конуса. |

4. Длина образующей конуса равна 2 см, а угол при вершине осевого сечения конуса равен 120 0 . Найдите площадь основания конуса.

В=120 0 ,L=2 см

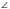
S_осн=R 2 =AC 2 L=AB=2 рассм. АВО, О=90 0

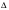
АС=R=Lsin60 0 =2 * /2=3 S_осн=3 2 =9 (см 2 ) Ответ: 9 (см 2 )

5. Радиус сектора равен 3 м, его угол 120 0 . Сектор свернут в коническую поверхность. Найдите радиус основания конуса.

S_бок=S_сеч S_сеч= * = *120 0 =3 R_сек=L_к

S_бок=3=R_кL=R_к*3 R_к=1(м) Ответ: 1 м.

Образующая конуса равна 6 м, а угол между нею и плоскостью основания равен 60 0 . Найдите площадь основания конуса.

Найдите площадь сечения конуса плоскостью, параллельной основанию и проходящей через середину высоты, если радиус основания равен 10 см.

Радиусы оснований усеченного конуса 3 дм и 7 дм, образующая 5 дм. Найдите площадь осевого сечения.

Образующая конуса 5 см, радиус основания 4 см. Определите площадь поверхности конуса.

Высота конуса 20 см, радиус основания 15 см. Определите площадь боковой поверхности конуса.

Образующая конуса 5 см и наклонена к плоскости основания под углом 30 0 . Определите высоту конуса.

Радиусы оснований усеченного конуса R и r, образующая наклонена под углом 45 0 . Найдите площадь поверхности усеченного конуса.

Осевым сечением конуса является треугольник с высотой 16 см и боковой стороной 20 см. Найдите площадь основания конуса.

Длина радиуса основания конуса 3 м, высота 4 м. Определите образующую конуса.

Высота конуса 20 см, а радиус его основания 25 см. Найдите площадь сечения конуса плоскостью параллельной основанию, и отстоящей от вершины конуса на расстояние 4 см.

Образующая конуса наклонена к плоскости основания под углом 60 0 . Найдите полную поверхность конуса при = .

Площадь оснований усеченного конуса 4 м 2 и 16 м 2 . Через середину высоты проведена плоскость параллельно основанию. Найдите площадь сечения.

Образующая конуса наклонена к плоскости основания под углом 45 0 . Радиус основания конуса равен 13 см. Найдите высоту конуса.

В усеченном конусе высота 63 дм, образующая 65 дм и боковая поверхность 26 м 2 . Определить радиусы оснований.

Площадь боковой поверхности конуса равна 11, а длина образующей . Найдите площадь основания конуса.

Угол при основании осевого сечения конуса 60 0 , высота конуса 3. Найдите боковую поверхность конуса.

Какая фигура получится при вращении прямоугольного треугольника вокруг одного из его катетов?

Назовите сечения конуса плоскостью.

Какие виды усеченного конуса вы знаете?

Можно ли вращением произвольного треугольника вокруг одной из его сторон получить конус?

Объясните, что такое усеченный конус?

Какой конус называется правильным?

Что такое радиус конуса, высота конуса, ось конуса, осевое сечение конуса?

Выведите формулу для вычисления площади поверхности конуса.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Решение задач на нахождение объема конуса — Объем наклонной призмы, пирамиды и конуса — ОБЪЕМЫ ТЕЛ

— закрепить знания и умения по теме «Объем конуса»;

— совершенствовать навыки решения задач.

I. Организационный момент

Сообщить тему урока, сформулировать цели урока.

II. Актуализация знаний учащихся

1. Проверка домашнего задания: у доски — № 708, дополнительная задача, вывод формулы Vk и Vус.к.; с места — № 701, 704.

2. Решение задач по готовым чертежам.

3. Решение задач у доски и в рабочих тетрадях.

III. Самостоятельная работа с последующей самопроверкой

IV. Подведение итогов

1. Записать домашнее задание.

П. 70, № 702, 705, 703.

Домашняя контрольная работа (см. приложение)

Дети получают ксерокопии домашних контрольных задач.

1. Проверка домашнего задания.

Задача № 701. Пусть h, r и V соответственно высота, радиус основания и объем конуса. Найдите: а) V, если h = 3 см, r = 1,5 см; б) h, если r = 4 см, V = 48π см3; в) r, если h = m, V = p.

a) (Ответ: V = 2,25π см3.)

б) из формулы (Ответ: h = 9 см.)

в) из формулы (Ответ: )

Задача № 708. Радиусы оснований усеченного конуса равны 3 м и 6 м, а образующая равна 5 м. Найдите объем конуса.

Дано: усеченный конус, r = О1С = 3 м, ОВ = R = 6 м, СB = 5 м (рис. 1).

Решение: Проведем СС1 ⊥ АВ, O1С = OС1 = 3 м, C1B = 6 — 3 = 3 (м). Из ΔСВС1 (∠C1 = 90°) по теореме Пифагора отсюда

Задача № 704. Дано: конус, h = SO = AB = H (рис. 2).

Решение: (Ответ: )

Дополнительная задача: Равносторонний треугольник вращается вокруг своей стороны а. Найдите объем полученного тела вращения.

Дано: ΔАВС, АВ = ВС = АС = а, АС — ось вращения (рис. 3).

Найти: объем тела вращения.

Решение: Объем тела вращения равен сумме объемов двух равных конусов. (из ΔAOB (∠O = 90°) по теореме Пифагора (Ответ: )

Заслушать учащихся, выводивших формулы для Vк и Vус.к..

2. Решение задач по готовым чертежам.

№ 1. Установите соответствие фигур и формул для нахождения объема (рис. 4 а), б), в)).

№ 2. Образующая конуса равна 60 см, высота 30 см. Найдите Vк (рис. 4).

Решение: Из ΔАOР (∠O = 90°): Так как РО = 1/2АР, то (Ответ: V = 27000π см3.)

№ 3. Образующая конуса, равна 12 см, наклонена к плоскости основания под углом 30° (рис. 5).

Найдите объем конуса.

Решение: Из ΔАSO (∠O = 90°): (Ответ: V= 216π см3.)

№ 4. Радиус оснований усеченного конуса 6 см и 10 см. Образующая наклонена к плоскости большего основания под углом 60°.

Дано: α = 60°, R = 10 см, r = 6 см (рис. 6).

Решение: (Ответ: )

№ 5. Образующая конуса 8 см, а угол при вершине осевого сечения 60°.

Найдите объем конуса.

Решение: (рис. 7):

(Ответ: )

№ 6. Найдите объем усеченного конуса, если его осевое сечение трапеция с основаниями 8 см, 6 см и высотой 3 см (рис. 8).

Решение: (Ответ: V = 37π см3.)

3. Решение задач у доски и в рабочих тетрадях.

№ 1. Доказать, что если прямой круговой конус пересечь плоскостью, параллельной основанию, то площади сечения и основания будут относиться как квадраты их расстояний от вершины.

Дано: конус, S — площадь основания, S1 — площадь сечения (рис. 9).

Доказать:

Решение: Сечением прямого кругового конуса плоскостью, параллельной основанию, является круг. Осевым сечением конуса является равнобедренный треугольник.

Из подобия ΔASB и ΔA1S1B1 (рис. 10) находим следовательно,

Что и требовалось доказать.

(Ответ: задача доказана.)

№ 2. Разность между образующей конуса и его высотой равна d, а угол между ними равен α. Найдите объем конуса.

Дано: конус, SO — высота, SB — образующая. SB — SO = d, ∠BSO = α (рис. 11).

Решение: Из ΔSOB (∠O = 90°): По условию SB — SO = d. Имеем Итак,

(Ответ: )

№ 3. Усеченный конус, у которого R1 = 22 см, R2 = 4 см, требуется превратить в равновеликий цилиндр такой же высоты. Чему равен радиус основания этого цилиндра?

Дано: цилиндр, усеченный конус, R1 = 22 см, R2 = 4 см, Vц. = Vк.

Найти: R (радиус цилиндра).

Решение: Н — общая высота тел, R — радиус цилиндра. Vц. = Vк., (Ответ: R = 14 см.)

Самостоятельная работа (см. приложение)

Ответы к задачам самостоятельной работы:

Вариант I. V = 24π см3. V = 9π м3

Вариатн II.

Решение самостоятельной работ.

№ 1. Из ΔCBD (∠D = 90°); Из ΔSCB: Из ΔSOB (∠O = 90°): (Ответ: V = 24π см3.)

№ 2. Дано: конус, ΔАРВ — осевое сечение, АР = РВ, ∠P = 90°. SΔAPB = 9 м2 (рис. 14).

Решение: Н = РО, R = АО, l — образующая конуса, ∠A + ∠B = 90°, ∠A = ∠B = 45°. Из ΔАРО (∠O = 90°): ∠APO = ∠PAO = 45°, значит, AO = PO = R = H. По теореме Пифагора (Ответ: V = 9π м3..

№ 1. Дано: усеченный конус, ВВ1 = 6 см, ∠BAB1 = 30°, ∠AB1B = 90° (рис. 15).

Решение: АВ = 12 см, R = ОВ = 6 см, ∠ABB1 = 60°. Проведем В1В2 ⊥ АВ. Из ΔBB1B2 (∠B2 = 90°): ∠B1 = 30°, значит, ВВ2 = 3 см, тогда, (Ответ: )

Решение домашней работы

№ 702. Дано: конус, РО = 5 см, РО1 = 2 см, V1 = 24 см3 (рис. 16).

Решение: Н = РО — высота конуса, V1 – объем меньшего конуса, АО = R, A1O1 = R. ΔРО1А1

ΔРОA, тогда,

(Ответ: V = 375 см3.)

№ 705. Дано: конус, ΔASB — осевое сечение, SΔASB = 60 см2, SB = SA = 13 см (рис. 17).

Решение: Из ΔSOB (∠O = 90°): Из (1) и (2):

тогда При R = 5, H = 12, тогда (Ответ: 240π см3 или 100π см3.)

№ 703. Дано: конус, Sосн. = Q, Sбок. = Р (рис. 18).

Решение: где R — радиус основания, H — высота. l — образующая,

(Ответ: )

Решение домашней контрольной работ.

№ 1. Дано: ΔАВС, АС = ВС = a, ∠C = α. l || СВ, l — ось вращения (рис. 19).

Найти: объем полученного тела вращения.

Решение: Проведем CL || l и ВK ⊥ l, тогда Vтела = Vu – V1 — V2, где Vu – объем цилиндра, полученного вращением прямоугольника KBCL, V1 и V2 — объемы конусов, образующихся вращением ΔАКВ и ΔALC. так как LC = КВ, a BC = AK + AL, то ВС = а, Из ΔALC (∠L = 90°) : LC = asinα, поэтому (Ответ: )

№ 2. Дано: конус, АР = √6 см, ∠PAB = 45° (рис. 20).

Решение: R = AO, H = РО. Из ΔAОР ((∠O = 90°): ∠APO = 45°, значит, AO = PO = R=H. По теореме Пифагора 2R2 = 6, R2 = 3, R = H = √3. (Ответ: V = π√3 см3.)

№ 3. Дано: цилиндр, конус, ОВ = O1В1 = 2,5 м, SO1 = 4 м, ОО1 = 2,2 м, ρ = 0,03 г/см3 (рис. 21).

Решение: где

(Ответ: 1,6 т — масса стога сена.)

№ 4. Дано: конус, R — радиус основания, усеченный конус, R — радиус основания (рис. 22).

Найти:

Решение: ΔSA1O1

ΔSAO, значит, отсюда

(Ответ: )

№ 5. Дано: два конуса, O1 = О — центры оснований, ∠ASO = ∠A1S1O1 = α, ОА = R. Sбок.внут.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.