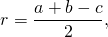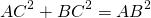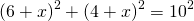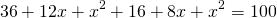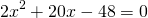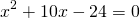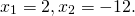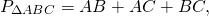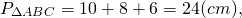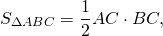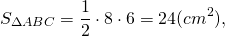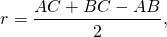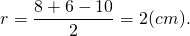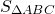задача №693
к главе «Глава VIII. Окружность. §4. Вписанная и описанная окружности».
Выделите её мышкой и нажмите CTRL + ENTER
Большое спасибо всем, кто помогает делать сайт лучше! =)
Нажмите на значок глаза возле рекламного блока, и блоки станут менее заметны. Работает до перезагрузки страницы.
Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать
Узнать ещё
Знание — сила. Познавательная информация
Видео:№ 693 - Геометрия 7-9 класс АтанасянСкачать

Окружность, вписанная в прямоугольный треугольник
Если в задаче дана окружность, вписанная в прямоугольный треугольник, то ее решение может быть связано со свойством отрезков касательных, проведенных из одной точки, и теоремой Пифагора.
Кроме того, следует учесть, что радиус вписанной в прямоугольный треугольник окружности вычисляется по формуле
где a и b — длины катетов, c — гипотенузы.
Рассмотрим две задачи на вписанную в прямоугольный треугольник окружность.
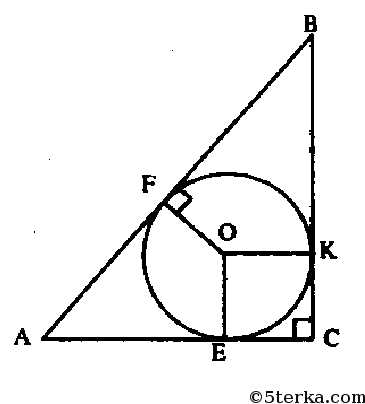
Точка касания окружности, вписанной в прямоугольный треугольник, делит гипотенузу на отрезки 4 см и 6 см. Найти периметр и площадь треугольника и радиус окружности.

окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) По свойству отрезков касательных, проведенных из одной точки,

2) AB=AM+BM=6+4=10 см,
3) По теореме Пифагора:
Второй корень не подходит по смыслу задачи. Значит, CK+CF=2 см, AC=8 см, BC=6 см.
Ответ: 24 см, 24 см², 2 см.
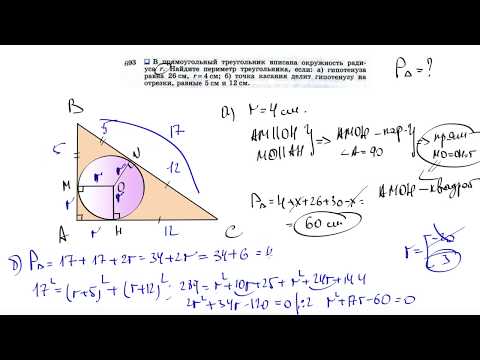
Найти площадь прямоугольного треугольника, гипотенуза которого равна 26 см, а радиус вписанной окружности — 4 см.

окружность (O, r) — вписанная,
K, M, F — точки касания со сторонами AC, AB, BC,
1) Проведем отрезки OK и OF.
(как радиусы, проведенные в точки касания).
Четырехугольник OKCF — прямоугольник (так как у него все углы — прямые).
А так как OK=OF (как радиусы), то OKCF — квадрат.
2) По свойству касательных, проведенных из одной точки,
3) AC=AK+KC=(x+4) см, BC=BF+CF=26-x+4=(30-x) см.
Видео:Задача 6 №27624 ЕГЭ по математике. Урок 71Скачать

В прямоугольный треугольник с гипотенузой, равной 26, вписана окружность радиуса 4. Найдите периметр треугольника.
Расстояние от вершины прямого угла данного треугольника до точки касания вписанной окружности с катетом треугольника равно радиусу вписанной окружности (r = 4).
С другой стороны, это расстояние равно p — c, где p — полупериметр треугольника, а c — гипотенуза (c = 26). Следовательно, r = p — c, или 4 = p — 26. Поэтому p = 30, а периметр треугольника равен 60.

Ответ
📺 Видео
РАДИУС вписанной окружности #математика #огэ #огэматематика #данирСкачать

Окружность вписанная в треугольник и описанная около треугольника.Скачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

ЕГЭ Математика Задание 6#27935Скачать

Формулы для радиуса окружности #shortsСкачать

Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать
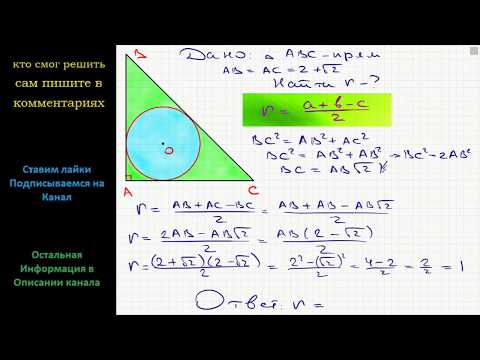
Вписанный в окружность прямоугольный треугольник.Скачать

15 задание треугольники огэ по математике / маттаймСкачать

Равносторонний треугольник в окружностиСкачать

Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

Окружность вписана в равносторонний треугольник, найти радиусСкачать

№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

Окружность вписана в равнобедренный треугольник. Найти её радиус.Скачать

Найдите гипотенузуСкачать

ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК И ОКРУЖНОСТЬСкачать

🔴 Радиус вписанной в прямоугольный треугольник ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать