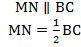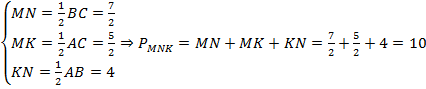Прямая проходящая через середину стороны треугольника параллельная основанию

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Видео:Средняя линия. Теорема о средней линии треугольникаСкачать

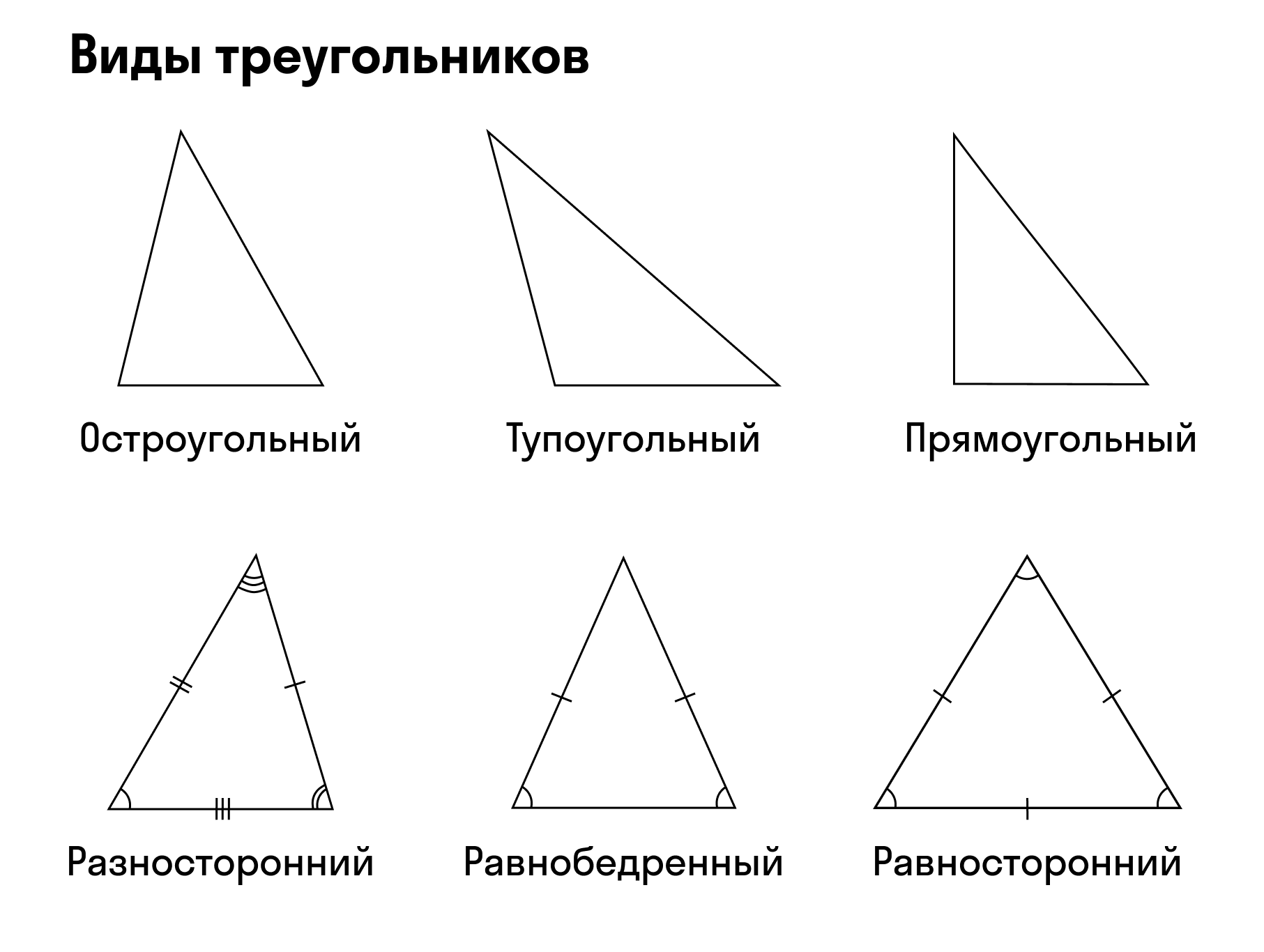
Понятие треугольника

Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, которые не лежат на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.

• Прямоугольный. Один угол прямой, то есть равен 90 градусам, два других меньше 90 градусов.
• Остроугольный. Градусная мера всех углов больше 0, но меньше 90 градусов.
• Тупоугольный. Один угол тупой, два других — острые.

Треугольник считают равнобедренным, если две его стороны равны. Эти стороны называют боковыми сторонами, а третью — основанием.

Треугольник, у которого все стороны равны, называется равносторонним или правильным.

Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, которая лежит напротив прямого угла — гипотенуза, а две другие стороны — катеты.

Правильный (равносторонний или равноугольный) треугольник — это правильный многоугольник, в котором все стороны равны между собой, все углы также равны и составляют 60°. В равностороннем треугольнике высота является и биссектрисой, и медианой.

Свойства треугольников:

• В треугольнике против большего угла лежит большая сторона — и наоборот.
• Сумма углов треугольника равна 180 градусов.
• Все углы равностороннего треугольника равны 60 градусам.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Видео:№204 Концы отрезка АВ лежат на параллельных прямых а и b. Прямая, проходящая через середину ОСкачать

Понятие средней линии треугольника

Определение средней линии треугольника подходит для любого вида этой фигуры.

​Средняя линия треугольника — отрезок, который соединяет середины двух сторон. В любом треугольнике можно провести три средних линии.

​Основанием считается сторона, которой параллельна средняя линия.

Как найти среднюю линию треугольника — расскажем дальше, а для начала еще немного разберемся со всеми определениями.

Видео:№241. Прямая, параллельная основанию равнобедренного треугольника ABC, пересекает боковые стороны АВСкачать

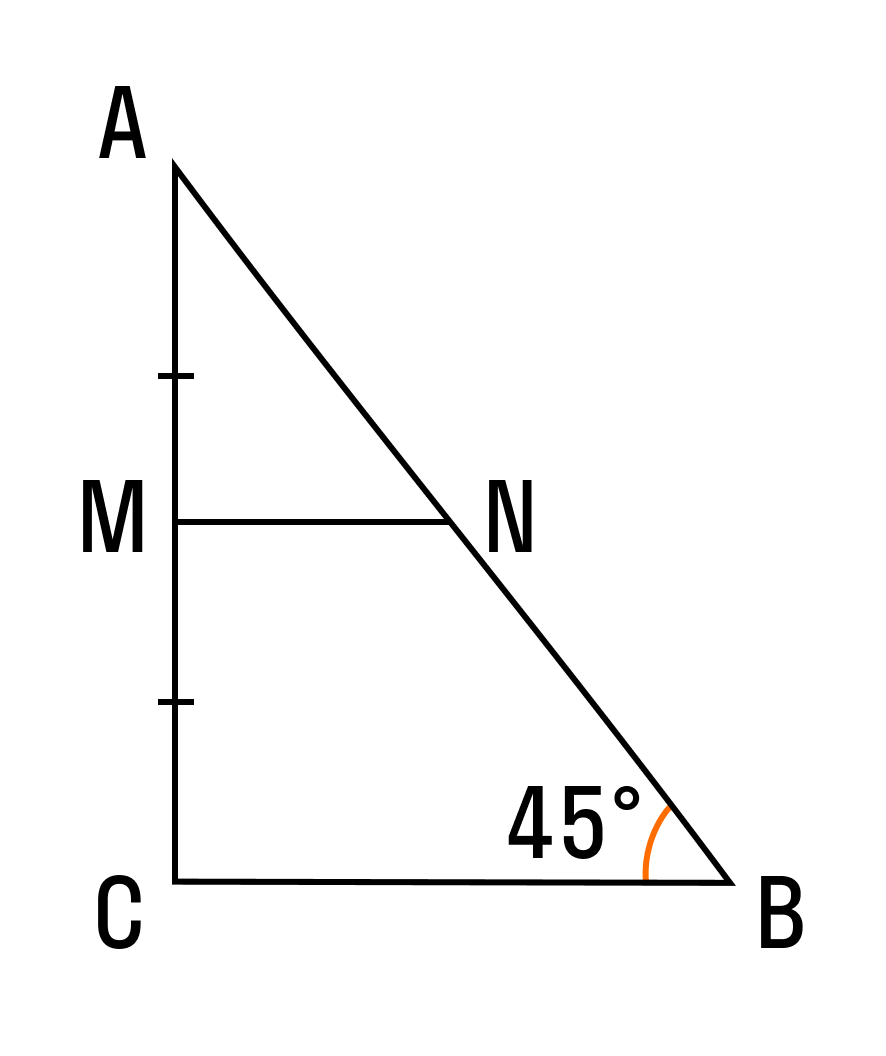
Понятие средней линии прямоугольного треугольника

Математики говорят: в любом треугольнике можно провести три средних линии. В прямоугольном треугольнике этот отрезок будет равен половине основания — это и есть формула средней линии прямоугольного треугольника.

Прямой угол помогает нам применить другие признаки равенства и подобия. Для углов в прямоугольном треугольнике можно использовать геометрические тождества без дополнительных построений, а любую из сторон можно найти по теореме Пифагора.

В прямоугольном треугольнике две средние линии перпендикулярны катетам, а третья равна медиане, проведенной к гипотенузе. Средние линии острого и разностороннего треугольника не обладают подобными свойствами.

Видео:№204. Прямая ОМ перпендикулярна к плоскости правильного треугольника ABC и проходит через центр ОСкачать

Свойства средней линии треугольника

Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

Свойства:

1. Средняя линия равна половине длины основания и параллельна ему.
2. Средняя линия отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Теорема о средней линии треугольника

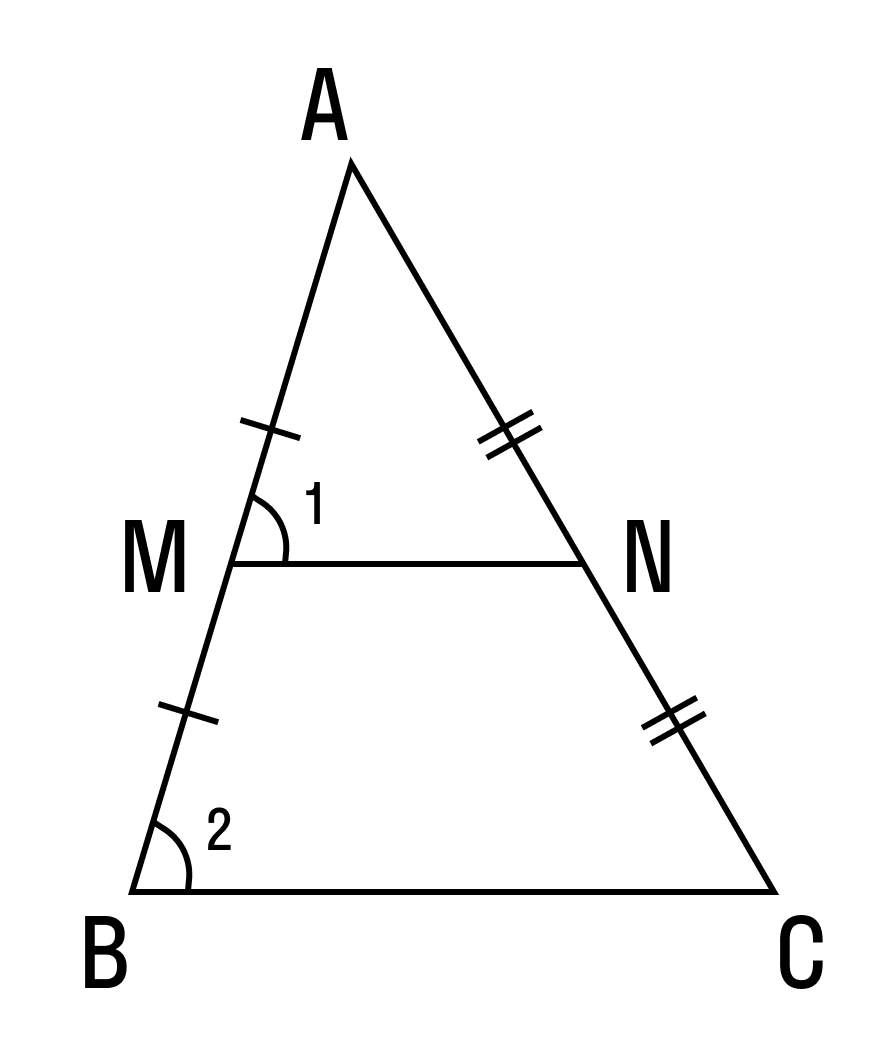
Теорема о средней линии треугольника звучит так:

Средняя линия треугольника параллельна основанию и равна его половине. А так выглядит формула нахождения средней линии треугольника:

Докажем теорему:

По условию нам дано, что MA = MB, NA = NC

Рассмотрим два образовавшихся треугольника ΔAMN и ΔABC.

(по второму признаку подобия треугольников).

△ABC, то Следовательно, ВС = 2МN. Значит, доказано, что средняя линия равна половине основания.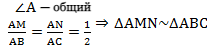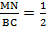

△ABC, то ∠1 = ∠2 . Так как ∠1 и ∠2 — соответственные углы, то по признаку параллельности прямых MN || BC.

Параллельность средней линии и соответствующего ей основания доказана.

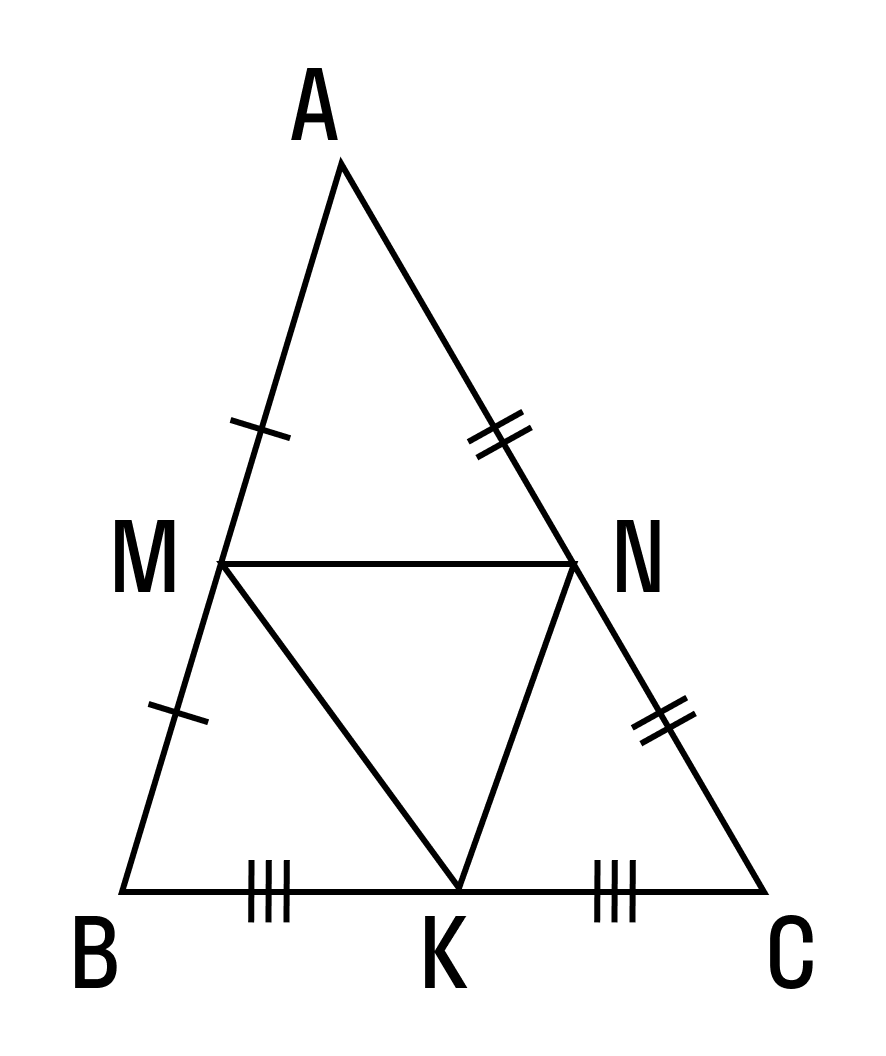
Пример 1. В треугольнике ΔABC AB = 8, BC = 7, CA = 5, точки M, K, N — середины сторон AB, BC, CA соответственно. Найти периметр ΔMNK.

Соединим середины сторон треугольника ΔABC и получим его средние линии, которые образуют треугольник ΔMNK. Найдем их длины по теореме о средней линии:

Ответ: периметр треугольника ΔMNK равен 10.

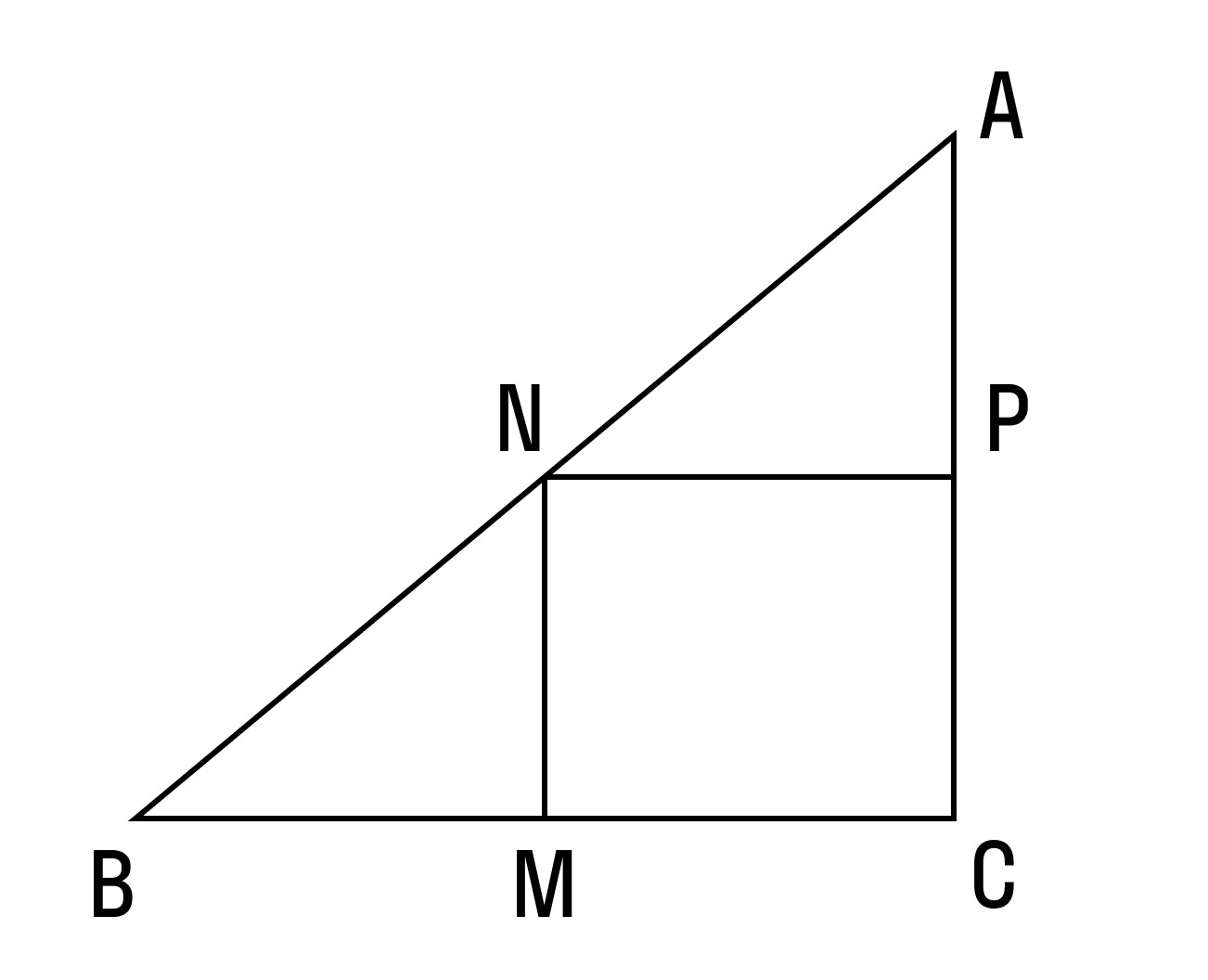
Пример 2. В прямоугольном треугольнике АВС есть две средние линии: MN и NP, равные 3 и 4 соответственно. Найти площадь большого прямоугольного треугольника.

Площадь треугольника равна половине произведения основания на высоту. Так как треугольник прямоугольный, то его площадь найдем как половину произведения катетов:

Так как MN — средняя линия, то по теореме о средней линии она равна половине катета AC:

Значит, AC = 2MN = 2 × 3 = 6.

Так как NP — средняя линия, то по теореме о средней линии она равна половине катета BC:

Значит, BC = 2NP = 2 × 4 = 8.

Тогда найдем площадь большого треугольника, используя формулу, указанную выше:

S = ½ × 6 × 8 = ½ × 48 = 24.

Ответ: площадь большого прямоугольного треугольника равна 24.

Видео:Средняя линия треугольника и трапеции. 8 класс.Скачать

Прямая проходящая через середину стороны треугольника параллельная основанию

Напомним свойства трапеции, которые часто используются при решении задач. Некоторые из этих свойств были доказаны в заданиях для 9-го класса, другие попробуйте доказать самостоятельно. Приведённые рисунки напоминают ход доказательства.

$$ 4.^$$. Диагонали трапеции разбивают её на четыре треугольника с общей вершиной (рис. 20). Площади треугольников, прилежащих к боковым сторонам, равны, а треугольники прилежащие к основаниям — подобны.

$$ 4.^$$. В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжении боковых сторон, лежат на одной прямой (на рис. 21 точки `M`, `N`, `O` и `K`).

$$ 4.^$$. В равнобокой трапеции углы при основании равны (рис. 22).

$$ 4.^$$. В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции (рис. 23).

$$ 4.^$$. В равнобокой трапеции диагонали равны (рис. 24).

$$ 4.^$$. В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой – их полусумме

(рис. 25, основания равны `a` и `b`, `a>b`).

$$ 4.^$$. Во всякой трапеции середины боковых сторон и середины диагоналей лежат на одной прямой (рис. 26).

$$ 4.^$$. Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований (рис. 27).

$$ 4.^$$.В равнобокой трапеции `d^2=c^2+ab`, где `d` — диагональ, `c` — боковая сторона, `a` и `b` основания.

Во всякой трапеции сумма квадратов диагоналей равна сумме квадратов боковых сторон и удвоенного произведения оснований, т. е. `d_1^2+d_2^2=c_1^2+c_2^2+2*ab`.

$$ 4.^$$. Во всякой трапеции с основаниями `a` и `b` отрезок с концами на боковых сторонах, проходящий через точку пересечения диагоналей параллельно основаниям, равен `(2ab)/(a+b)` (на рис. 28 отрезок `MN`).

$$ 4.^$$. Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.

Докажем, например, утверждение $$ 4.^$$ .

Применяем теорему косинусов (см. рис. 29а и б):

`ul(DeltaACD):` `d_1^2=a^2+c_2^2-2a*c_2*cos varphi`,

`ul(DeltaBCD):` `d_2^2=b^2+c_2^2+2b*c_2*cos varphi` (т. к. `cos(180^@-varphi)=-cos varphi`).

Проводим `CK«||«BA` (рис. 29в), рассматриваем треугольник `ul(KCD):` `c_1^2=c_2^2+(a-b)^2-2c_2*(a-b)*cos varphi`. Используя последнее равенство, заменяем выражение в скобках в (2), получаем:

В случае равнобокой трапеции `d_1=d_2`, `c_1=c_2=c`, поэтому получаем

Отрезок, соединяющий середины оснований трапеции, равен `5`, одна из диагоналей равна `6`. Найти площадь трапеции, если её диагонали перпендикулярны.

`AC=6`, `BM=MC`, `AN=ND`, `MN=5` (рис. 30а). Во всякой трапеции середины оснований и точка пересечения диагоналей лежат на од-ной прямой (свойство $$ 4.^$$). Треугольник `BOC` прямоугольный (по условию `AC_|_BD`), `OM` — его медиана, проведённая из вершины прямого угла, она равна половине гипотенузы: `OM=1/2BC`. Аналогично устанавливается `ON=1/2AD`, поэтому `MN=1/2(BC+AD)`. Через точку `D` проведём прямую, параллельную диагонали `AC`, пусть `K` — её точка пересечения с прямой `BC` (рис. 30б).

По построению `ACKD` — параллелограмм, `DK=AC`, `CK=AD` и `/_BDK=90^@`

(т. к. угол `BDK` — это угол между диагоналями трапеции).

Прямоугольный треугольник `ul(BDK)` с гипотенузой `BK=BC+AD=2MN=10` и катетом `DK=6` имеет площадь `S=1/2DK*BD=1/2DKsqrt(BK^2-DK^2)=24`. Но площадь треугольника `BDK` равна площади трапеции, т. к. если `DP_|_BK`, то

Диагонали трапеции, пересекаясь, разбивают её на четыре треугольника с общей вершиной. Найти площадь трапеции, если площади треугольников, прилежащих к основаниям, равны `S_1` и `S_2`.

Пусть `BC=a`, `AD=b`, и пусть `h` — высота трапеции (рис. 31). По свойству $$ 4.^$$ `S_(ABO)=S_(CDO)`, обозначим эту площадь `S_0` (действительно, `S_(ABD)=S_(ACD)`, т. к. у них общие основания и равные высоты, т. е. `S_(AOB)+S_(AOD)=S_(COD)+S_(AOD)`, откуда следует `S_(AOB)=S_(COD)`). Так как `S_(ABC)=S_0 + S_1=1/2ah` и `S_(ACD)=S_0+S_2=1/2bh`, то `(S_0+S_1)/(S_0 + S_2)=a/b`.

Далее, треугольники `BOC` и `DOA` подобны, площади подобных треугольников относятся как квадраты соответствующих сторон, значит, `(S_1)/(S_2)=(a/b)^2`. Таким образом, `(S_0+S_1)/(S_0+S_2)=sqrt((S_1)/(S_2))`.Отсюда находим `S_0=sqrt(S_1S_2)`, и поэтому площадь трапеции будет равна

Основания равнобокой трапеции равны `8` и `10`, высота трапеции равна `3` (рис. 32).

Найти радиус окружности, описанной около этой трапеции.

Трапеция равнобокая, по свойству $$ 4.^$$ около этой трапеции можно описать окружность. Пусть `BK_|_AD`, по свойству $$ 4.^$$

Из прямоугольного треугольника `ABK` находим `AB=sqrt(1+9)=sqrt(10)` и `sinA=(BK)/(AB)=3/(sqrt10)`. Окружность, описанная около трапеции `ABCD`, описана и около треугольника `ABD`, значит (формула (1), § 1), `R=(BD)/(2sinA)`. Отрезок `BD` находим из прямоугольного треугольника `KDB:` `BD=sqrt(BK^2+KD^2)=3sqrt(10)` (или по формуле `d^2=c^2+ab`), тогда

$$ 4.^$$. Площадь трапеции равна площади треугольника, две стороны которого равны диагоналям трапеции, а третья равна сумме оснований.

$$ 4.^$$. Если `S_1` и `S_2` — площади треугольников, прилежащих к основаниям, то площади треугольников, прилежащих к боковым сторонам равны `sqrt(S_1S_2)`, а площадь всей трапеции равна `(sqrt(S_1) +sqrt(S_2))^2`.

$$ 4.^$$. Радиус окружности, описанной около трапеции, находится по формуле `R+a/(2sin alpha)`, где `a` — какая-то сторона (или диагональ трапеции), `alpha` — смотрящий на неё вписанный угол.

Видео:Разбор Задачи №16 из работы Статград от 16 февраля 2022Скачать

Одна из сторон треугольника лежит в плоскости a?

Геометрия | 10 — 11 классы

Одна из сторон треугольника лежит в плоскости a.

Докажите, что прямая, проходящая через середины двух других сторон треугольника, параллельна плоскости a.

Дано : треугольник АВС, плоскость а, прямая с, пересекающая АВ и ВС в точках М и К.

АС принадлежит а.

Доказать : с параллельна а.

Если МА = МВ, КВ = КС, тогда МК — средняя линия и МК параллельна АС.

АС принадлежит а, следовательно с параллельна а(по теореме : Если прямая вне плоскости параллельна какой — нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости).

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Точка e не лежит в плоскости параллелограмма abcd?

Точка e не лежит в плоскости параллелограмма abcd.

Докажите, что прямая, проходящая через середины отрезков ea и eb, параллельна стороне cd.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Через сторону АС треугольника АВС проведена плоскость альфа?

Через сторону АС треугольника АВС проведена плоскость альфа.

В не принадлежит альфа.

Докажите, что прямая, проходящая через середины сторон АВ и ВС , параллельна плоскости альфа.

Видео:ОГЭ по математике, задание 26, тренировочный вариант 1Скачать

Через середины 2 медиан треугольника проведена плоскость, не совпадающая с плоскостью треугольника?

Через середины 2 медиан треугольника проведена плоскость, не совпадающая с плоскостью треугольника.

Докажите, что проведённая плоскость параллельна одной из сторон треугольника.

Видео:Уравнения стороны треугольника и медианыСкачать

Середины сторон CA и BA треугольника BCA лежат на плоскости а (альфа), а сторона BC не лежит в этой плоскости?

Середины сторон CA и BA треугольника BCA лежат на плоскости а (альфа), а сторона BC не лежит в этой плоскости.

Докажите, что прямая BC и плоскость а(альфа) параллельны.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Через сторону AC треугольника ABC проведена плоскость α?

Через сторону AC треугольника ABC проведена плоскость α.

Докажите, что прямая, проходящая через середины AB и BC, параллельна плоскости α.

Видео:№31. Плоскость α параллельна стороне ВС треугольника ABC и проходит черезСкачать

Две стороны треугольника параллельны плоскости а?

Две стороны треугольника параллельны плоскости а.

Докажите, что и третья сторона параллельна плоскости а.

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Одна из сторон треугольника лежит в плоскости альфа доказать что прямая проходящая через середину двух других сторон треугольника паралельна?

Одна из сторон треугольника лежит в плоскости альфа доказать что прямая проходящая через середину двух других сторон треугольника паралельна.

Видео:Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

1. Середины сторон CD и BD треугольника BCD лежат в плоскости , а сторона ВС не лежит в этой плоскости : Докажите, что прямая ВС и плоскость параллельны?

1. Середины сторон CD и BD треугольника BCD лежат в плоскости , а сторона ВС не лежит в этой плоскости : Докажите, что прямая ВС и плоскость параллельны.

2. Точки А, В, С и D не лежат в одной плоскости.

Докажите, что любые три из них не лежат на одной прямой.

3. Прямая ^ КМ параллельна стороне ВС параллелограмма ABCD и не лежит в плоскости AВС.

Выясните взаимное расположение прямых КМ и AВ и найдите угол между ними, если AВС = 110°.

Видео:Биссектриса трапеции проходит через середину боковой стороны (Задача №324603)Скачать

Через сторону АС треугольника АВС проведена плоскость альфа?

Через сторону АС треугольника АВС проведена плоскость альфа.

В не принадлежит альфа.

Докажите, что прямая, проходящая через середины сторон АВ и ВС , параллельна плоскости альфа.

Видео:№160. Прямая а проходит через середину отрезка АВ и перпендикулярна к нему. Докажите, что: а) каждаяСкачать

Плоскость проходит через середины сторон треугольника и не совпадает с плоскостью этого треугольника?

Плоскость проходит через середины сторон треугольника и не совпадает с плоскостью этого треугольника.

Докажите, что данная плоскость параллельна третьей стороне треугольника + рисунок .

Заранее большое спасибо )).

На странице вопроса Одна из сторон треугольника лежит в плоскости a? из категории Геометрия вы найдете ответ для уровня учащихся 10 — 11 классов. Если полученный ответ не устраивает и нужно расшить круг поиска, используйте удобную поисковую систему сайта. Можно также ознакомиться с похожими вопросами и ответами других пользователей в этой же категории или создать новый вопрос. Возможно, вам будет полезной информация, оставленная пользователями в комментариях, где можно обсудить тему с помощью обратной связи.

💥 Видео

В каком отношении делит сторону BC треугольника ABC прямая, проходящая через A?Скачать

ОГЭ Задание 25 Средняя линия прямоугольного треугольникаСкачать

Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать