 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- Окружность. Относительное взаимоположение окружностей.
- Окружность и круг — определение и вычисление с примерами решения
- Определение окружности и круга
- Определение окружности и ее элементов
- Что такое окружность и круг
- Пример №3
- Окружность и треугольник
- Описанная окружность
- Вписанная окружность
- Пример №4
- Пример №5
- Геометрические построения
- Пример №6
- Пример №7
- Пример №8
- Пример №9
- Пример №10
- Пример №11
- Пример №12
- Пример №13
- Задачи на построение
- Пример №14
- Пример №15
- Пример №16
- Пример №17
- Свойство диаметра, перпендикулярного хорде
- Касательная к окружности
- Признак касательной
- Свойство отрезков касательных
- Касание двух окружностей
- Задачи на построение
- Основные задачи на построение
- Решение задач на построение
- Пример №18
- Геометрическое место точек
- Основные теоремы о ГМТ
- Метод геометрических мест
- Пример №19
- Описанная и вписанная окружности треугольника
- Окружность, вписанная в треугольник
- Пример №20
- Задачи, которые невозможно решить с помощью циркуля и линейки
- Циркуль или линейка
- Об аксиомах геометрии
- Метод вспомогательного треугольника
- Пример №21
- Пример №22
- Пример №23
- Реальная геометрия
- Справочный материал по окружности и кругу
- Что называют окружностью
- Окружность, вписанная в треугольник
- Окружность, описанная около треугольника
- Геометрическое место точек в окружности и круге
- Некоторые свойства окружности. Касательная к окружности
- 💥 Видео
Видео:№204 Концы отрезка АВ лежат на параллельных прямых а и b. Прямая, проходящая через середину ОСкачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Круг |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Радиус |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Хорда |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Диаметр |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Касательная |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Секущая |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:Разбор Задачи №16 из работы Статград от 22 апреля 2020Скачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Пересекающиеся хорды |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Касательные, проведённые к окружности из одной точки |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Секущие, проведённые из одной точки вне круга |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Пересекающиеся хорды | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
| Касательные, проведённые к окружности из одной точки | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
| Касательная и секущая, проведённые к окружности из одной точки | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
| Секущие, проведённые из одной точки вне круга | ||||||||||||||||||||||||||||||||||||||||
 | ||||||||||||||||||||||||||||||||||||||||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Доказательства теорем о длинах хорд, касательных и секущих
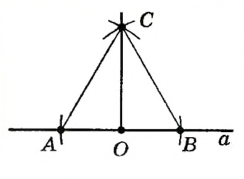
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Видео:№200. Докажите, что любая точка прямой, которая проходит через центр окружности, описанной около мноСкачать
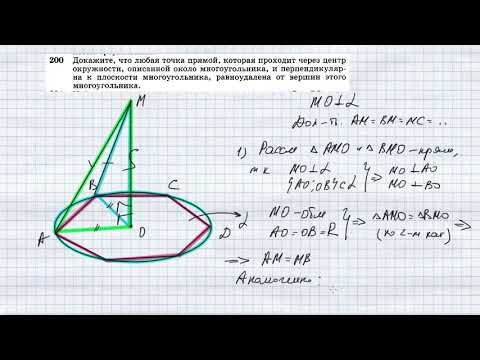
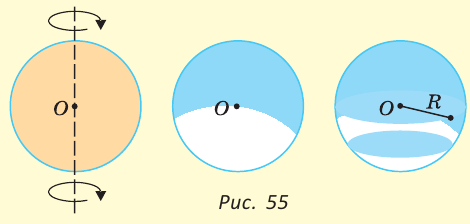
Окружность. Относительное взаимоположение окружностей.
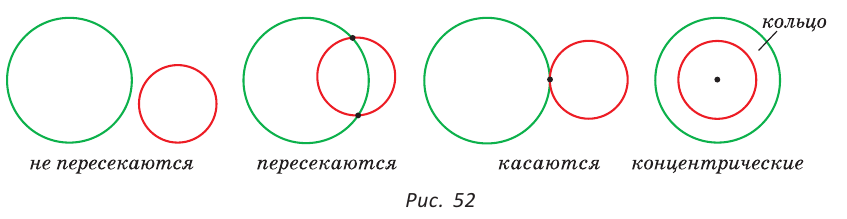
Если две окружности имеют только одну общую точку, то говорят, что они касаются.
Если же две окружности имеют две общие точки, то говорят, что они пересекаются.
Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.
Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1).
Теорема.
Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.
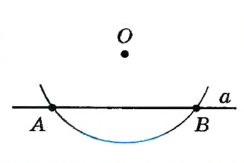
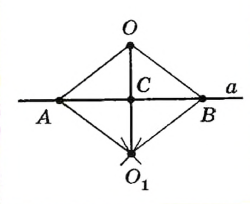
Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1.
Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются.
Следствие.
Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.
Теоремы.
1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.
2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.
Признаки различных случаев относительного положения окружностей.
Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d.
Эти окружности могут находиться в следующих 5-ти относительных положениях:
1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 .
2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1.
3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон.
4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1.
5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,
d R + R1, то окружности расположены одна вне другой, не касаясь.
2. Если d = R + R1, то окружности касаются извне.
3. Если d R — R1, то окружности пересекаются.
4. Если d = R — R1, то окружности касаются изнутри.
5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.
Видео:№968. Напишите уравнение окружности с центром в точке А(0; 6), проходящей через точку В (-3; 2).Скачать

Окружность и круг — определение и вычисление с примерами решения
Содержание:
Пусть в природе не существовало бы ни одного круга или треугольника, и все-таки истины, доказанные Евклидом, навсегда сохранили бы свою достоверность и очевидность.
Раньше вы знакомились с основными геометрическими фигурами, устанавливали особенности этих фигур и их взаимное расположение. Но на практике довольно часто приходится решать «обратную» задачу — по определенным особенностям находить фигуру, имеющую их. Именно таково содержание задач на построение, которые будут рассматриваться в этом разделе.
Еще в работах древнегреческих математиков описаны задачи на построение и методы их решения.
Многие из этих задач составляют классику евклидовой геометрии. Кроме практической ценности, такие задачи представляют значительный исследовательский интерес, поскольку в ходе их решения определяются новые особенности построенных фигур.
Окружность и круг:
Определение. Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от данной точки, которая называется центром окружности.
Радиусом окружности называется отрезок, соединяющий центр окружности с любой точкой на окружности (или длина этого отрезка).
Хордой окружности называется отрезок, соединяющий две точки окружности.
Диаметром окружности называется хорда, проходящая через центр окружности.
Дугой окружности называется часть окружности, ограниченная двумя точками.
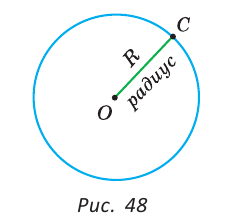
На рисунке 48 точка О — центр, отрезок ОС — радиус окружности. Радиус обозначают буквой R (или
На рисунке 49 изображены: хорда ЕН, дуга КМ (обозначается: 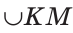
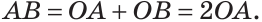
Любые две точки окружности разбивают ее на две дуги, которые дополняют друг друга до окружности. Эти дуги так и называются — дополнительными. Чтобы различать такие дуги, их иногда обозначают тремя буквами. На рисунке 49 дуги АКМ и АНМ — дополнительные.
Определение. Кругом называется часть плоскости, ограниченная окружностью.
Точки окружности также принадлежат кругу (рис. 50). Поэтому центр, радиус, хорда и диаметр у круга те же, что и у его окружности.
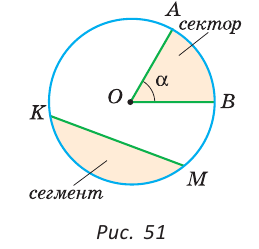
Часть круга, заключенная между двумя радиусами, называется сектором. Часть круга, заключенная между дугой окружности и хордой, соединяющей концы дуги, называется сегментом (рис. 51). Два радиуса разбивают круг на два сектора, хорда разбивает круг на два сегмента.
Полуокружностью называется дуга окружности, концы которой являются концами диаметра. Полукругом называется часть круга, ограниченная полуокружностью и диаметром, соединяющим концы полуокружности. На рисунке 49 дуга АКВ — полуокружность, сегмент АКВ — полукруг.
Угол, вершина которого находится в центре окружности, называется центральным углом. На рисунке 51 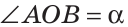
Окружности (круги) равны, если равны их радиусы.
Две окружности могут не иметь общих точек, могут пересекаться в двух точках или касаться друг друга в одной точке. Окружности разного радиуса с общим центром называются концентрическими. Часть плоскости между двумя концентрическими окружностями называется кольцом (рис. 52).
Видео:Окружность. 7 класс.Скачать

Определение окружности и круга
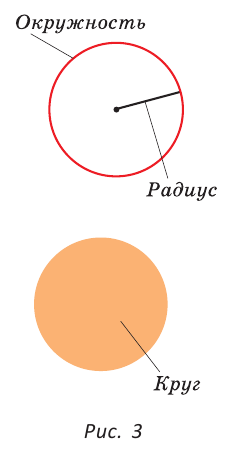
Окружность — это замкнутая линия на плоскости, все точки которой находятся на одинаковом расстоянии от одной точки — центра окружности.
Круг — это внутренняя часть плоскости, ограниченная окружностью.
Размеры окружности и круга определяются их радиусом — отрезком, который соединяет центр с точкой на окружности (рис. 3).
В математике «окружность» и «круг» — два различных, хотя и связанных между собой, понятия. Окружность, например, является моделью обруча, а круг — моделью крышки люка.
Определение окружности и ее элементов
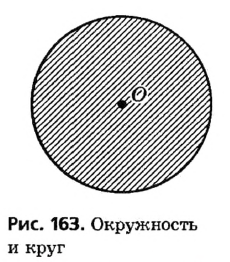
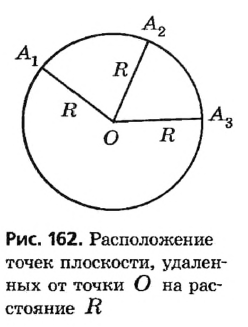
Пусть на плоскости отмечена точка О. Очевидно, что от точки О можно отложить бесконечное множество отрезков длиной R (рис. 162). Концы всех таких отрезков на плоскости образуют окружность — фигуру, уже известную из курса математики. Определение Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, удаленных от данной точки (центра окружности) на одинаковое расстояние. Иначе говорят, что все точки окружности равноудалены от ее центра. Определение Кругом называется часть плоскости, ограниченная окружностью и содержащая ее центр. Иначе говоря, круг состоит из всех точек плоскости, удаленных от данной точки (центра круга) на расстояние, не превышающее заданного. На рисунке 163 заштрихованная часть плоскости — круг, ограниченный окружностью с тем же центром. Центр окружности и круга является точкой круга, но не является точкой окружности.
Определение Радиусом окружности (круга) называется расстояние от центра окружности до любой ее точки. Радиусом также называется любой отрезок, соединяющий точку окружности с ее центром. На рисунке 162 
Радиус — от латинского «радиус» — луч, спица
Хорда — от греческого «хорда» — струна, тетива
Диаметр — от греческого «диа» — насквозь и «метрео» — измеряющий насквозь; другое значение этого слова — поперечник
Радиусом также называется любой отрезок, соединяющий точку окружности с ее центром. На рисунке 162 
Определение:
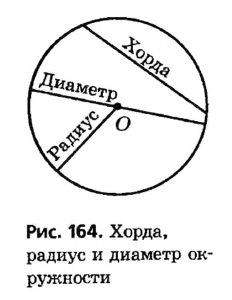
Хордой называется отрезок, соединяющий две точки окружности.
Диаметром называется хорда, проходящая через центр окружности.
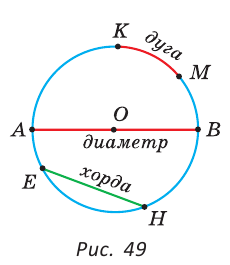
На рисунке 164 изображены две хорды окружности, одна из которых является ее диаметром. Обычно диаметр обозначают буквой d. Очевидно, что диаметр вдвое больше радиуса, то есть d = 2R.
Построение окружности выполняют с помощью циркуля.
Видео:Окружность данного радиуса, проходящей через две заданные точкиСкачать
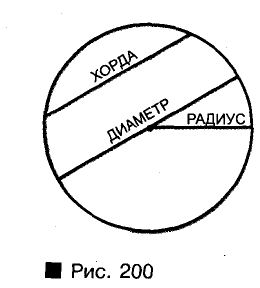
Что такое окружность и круг
Окружность — это фигура, состоящая из всех точек плоскости, равноудален ных от данной точки. Эту точку называют центром окружности.
Отрезок, соединяющий любую точку окружности с ее центром, называют ради усом. Отрезок, соединяющий две против вольные точки окружности, — хорда окружности. Хорда, проходящая через центр окружности, — диаметр (рис. 200). Каждый диаметр окружности состоит’ из двух радиусов, поэтому его длина вдвое больше длины радиуса. Длина хорды, не проходящей через центр окружности, меньше длины диаметра, (Почему?)
Окружность на бумаге описывают МА и MB — перпендикуляры на ОА и ОВ (см. рис. 216), то 
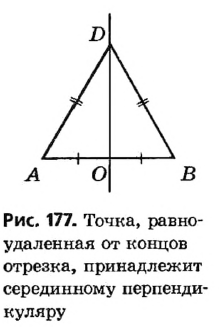
Геометрическим местом точек угла, равноудаленных от его сторон, является биссектриса этого угла.
Здесь имеются в виду углы меньше развернутого.
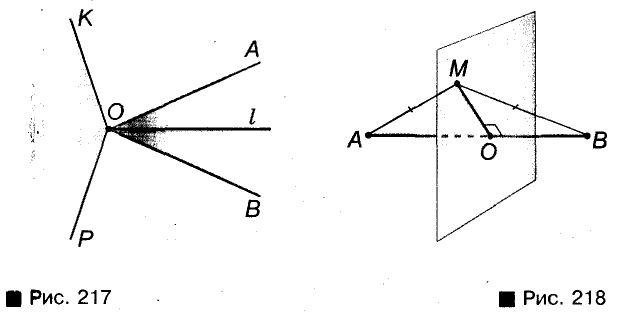
Верно ли, что геометрическим местом точек, равноудален-ных от сторон угла, является биссектриса этого угла? Нет. Когда в планиметрии говорят о геометрическом месте точек, не уточняя, о каких именно точках идет речь, то имеют в виду точки плоскости, которой принадлежит данная фигура. При таком условии геометрическим местом точек, равноудаленных от ф сторон угла, является объединение биссектрисы I данного угле g и всех точек некоего другого угла, показанного на рисунке 217,
Ведь каждая точка угла КОР также равноудалена от сторон донного угла АО В (речь идет об углах меньше развернутого).
Когда мы говорим, что геометрическим местом точек, равноудаленных от концов отрезка, является серединный перпендикуляр этого отрезка, то мы имеем в виду, что речь идет о геометрическом месте точек плоскости, на которой лежит отрезок.
А геометрическим местом точек пространства, равноудаленных от концов отрезка, является некая плоскость (мал. 218).
Подумайте, как расположена эта плоскость относительно денного отрезка.
Геометрические места точек пространства изучают в старших классах.
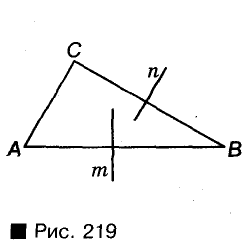
Пример №3
Докажите, что серединные перпендикуляры двух сторон треугольника пересекаются.
Решение:
Пусть n и m— серединные перпендикуляры сторон ВС и АВ треугольника (рис. 219). Докажем, что они не могут быть параллельны. Доказывать будем от противного. Допустим, что n || m. Тогда прямая, перпендикулярная к п, должна быть перпендикулярной и к m, то есть 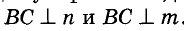
Окружность и треугольник
Окружность и треугольник могут не иметь общих точек или иметь 1, 2, 3, 4, 5, 6 общих точек (соответствующие рисунки выполните самостоятельно). Заслуживаем внимания случаи, когда окружность проходит через все три вершины треугольника или когда она касается всех и сторон треугольника. Рассмотрим такие случаи подробнее.
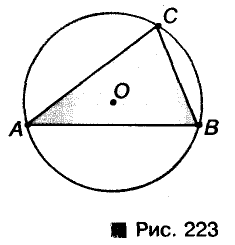
Описанная окружность
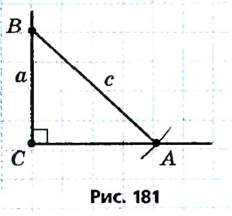
Окружность называется описанной около треугольника, если она проходит через все вершины треугольника (рис. 223).
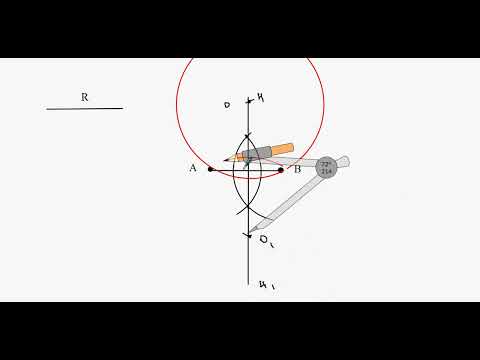
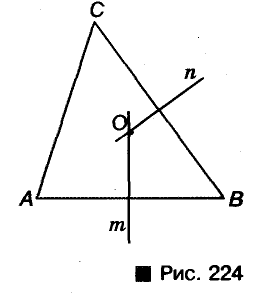
Теорема: Около каждого треугольника можно описать только одну окружность. Ее центром является точка пересечения серединных перпендикуляров двух сторон треугольника.
Пусть ABC — произвольный треугольник (рис. 224). Найдем точку, равноудаленную от вершин А, В и С.’ Метрическое место точек, равноудаленных от А и В, — серединный перпендикуляр m отрезка АВ; геометрическое место точек, равноудаленна от В и С, — серединный перпендикуляр n отрезка ВС. Эти два серединных перпендикуляра не могут быть параллельными, они пересекаются в точке О. А она равноудалена от Н и С. Следовательно, ОА = ОВ = ОС, поэтому О — центр окружности, описанной около ABC.
Для каждого отрезка АВ существует серединный перпендикуляр, и только один, а для ВС — серединный перпендикуляр и только один. И точка их пересечения существует всегда, только одна. Таким образом, около каждого треугольника можно описать одну окружность, и только одну.
- Серединные перпендикуляры всех трех сторон произвольного треугольника проходят через одну и ту же точку.
- Через любые три точки, не лежащие на одной прямой, можно провести окружность, и только одну.
Из доказанной теоремы следует cnocof построения окружности, описанной около треугольника. Чтобы описать около треугольника ABC окружность, достаточно:
- построить серединные перпендикуляры двух сторон данного треугольника;
- определить точку О, в которой эти серединные перпендикуляры пересекаются;
- ) из центра О провести окружность радиуса ОА.
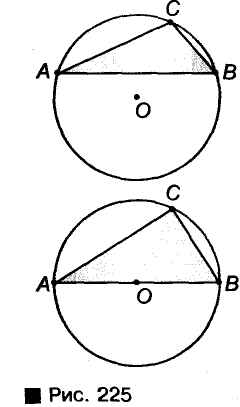
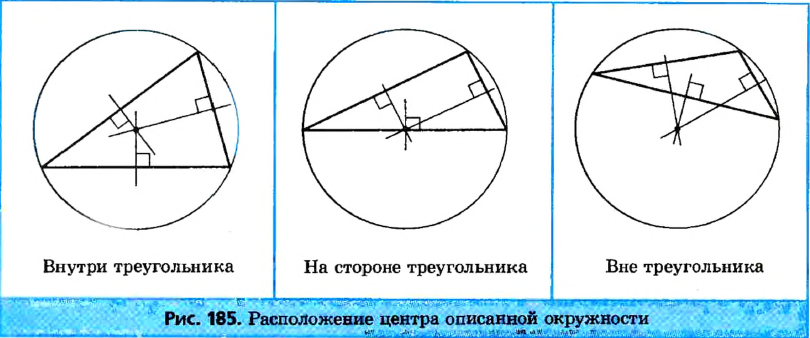
Центр окружности, описанной около треугольника, может лежать во внутренней или внешней области данного треугольника либо на его сторон (рис. 225).
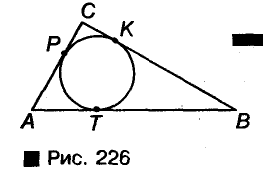
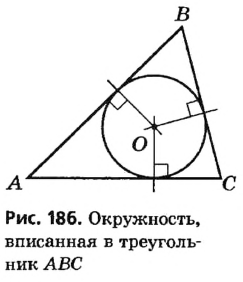
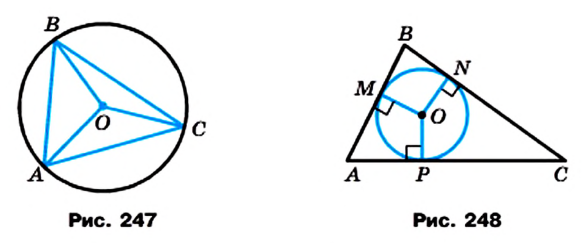
Вписанная окружность
Окружность называется вписанной в треугольник если она касается всех сторон треугольника (рис. 226). Центр окружности, вписанной в треугольник, лежим’ и внутренней области этого треугольник.
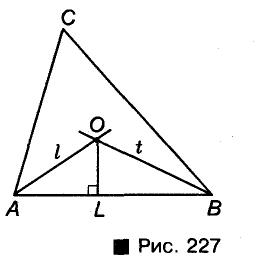
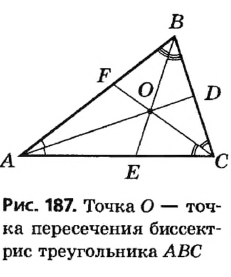
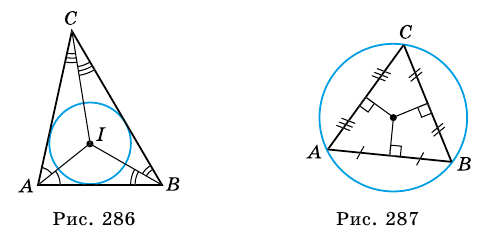
Теорема: В каждый треугольник можно вписан только одну окружность. Ее центром является точка пересечения двух биссектрис треугольника.
Доказательство:
Пусть ABC — произвольный треугольник. Определим точи О, равноудаленную от всех его сторон (рис. 227). Геометрическое место точек, лежащих внутри угла А и равноудаленных второй АВ и АС, — биссектриса l угла А. Гtjметрическое место точек, равноудаленных от сторон АВ и ВС и лежащих внутри угла В, — биссектриса t угла B. Эти две биссектрисы обязательно Пересекаются (докажите это!). Точка U, в которой пересекаются биссектрисы l и t, равноудалена от всех трех сторон данного треугольника. Следовательно, точка О — центр окружности, Вписанной в треугольник АВС.
В каждом треугольнике все три биссектрисы пересекаются в одной точке.
Из доказанной теоремы следует способ построения окружности, вписанной в треугольник. Чтобы вписать в данный треугольник окружность, достаточно:
- провести две его биссектрисы;
- из точки их пересечения О опустить перпендикуляр OL на произвольную сторону треугольника;
- из центра О радиуса OL описать окружность. Она касается каждой стороны треугольника, следовательно, является вписанной в данный треугольник.
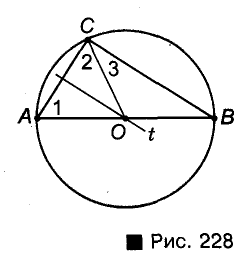
Теорема: Центром окружности, описанной около прямоугольного треугольника, является середина его гипотенузы.
Пусть ABC — произвольный треугольник с прямым углом С, t— серединный перпендикуляр катета АС, пересекающий гипотенузу АВ в точке О (рис. 228).
Поскольку точка О лежит на серединном перпендикуляре отрезка АС, то 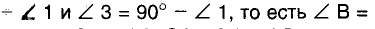
точка О—середина гипотенузы АВ, равноудаленная от всех вершин треугольника. Таким образом, окружность с центром О и радиусом ОА проходит через все вершины данного треугольника.
Диаметр окружности, описанной около прямоугольного треугольника, равен его гипотенузе.
Теорема: Из любой точки окружности ее Диаметр, не выходящий из этой точки, виден под прямым углом.
Доказательство:
Пусть АВ — произвольный диаметр окружности с центром О, а С— произвольная точка окружности, отличная от А и В (рис. 229). Покажем, что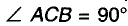
Геометрическим местом точек плоскости, из которых отрезок АВ виден под прямым углом, является окружность диаметра АВ. На самом деле этому ГМТ точки А и В не принадлежат. Подробнее об этом вы узнаете в старших классах.
Пример №4
Найдите радиус окружности, описанной около прямоугольного треугольника с гипотенузой 6 см.
Решение:
Диаметр окружности, описанной около прямоугольного треугольника, является его гипотенузой. Радиус вдвое меньше: 3 см.
Пример №5
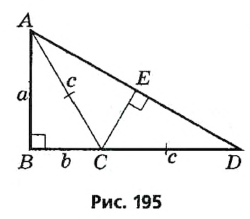
Докажите, что диаметр окружности, вписанной в прямоугольный треугольник с катетами а и Ь и гипотенузой с, равен a + b — c.
Решение:
Пусть в 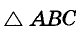
Геометрические построения
Пользуясь линейкой’ и циркулем, моле но выполнить много геометрических построений, то есть начертить геометрические фигуры. Рассмотрим сначала, как выполняются самые простые геометрические построения.
Пример №6
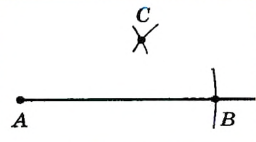
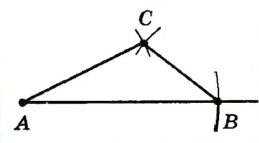
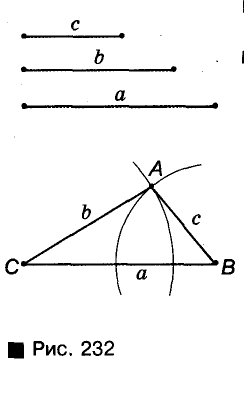
Постройте треугольник по данным сторонам.
Решение:
Пусть даны три отрезки а, b и с (рис. 232). Нужно построить, треугольник, стороны которого были бы равны этим отрезкам. С помощью линейки проводим произвольную прямую, обозначаем на ней произвольную точку В и циркулем откладываем на этой прямой отрезок ВС = а. Раствором циркуля, равным с описываем дугу окружности с центром В. С той же стороны от прямой СВ описываем дугу окружности радиуса b с центром С. Точку пересечения А этих дуг соединяем отрезками с С и В. Треугольник ABC — именно тот, который требовалось построить, так как его стороны ВС, АС и АВ равны данным отрезкам.
Если построенные дуги не пересекаются, требуемый треугольник построить невозможно. Это бывшие в том случае, когда один из данных отрезков больше суммы двух других или равен их сумме.
Пример №7
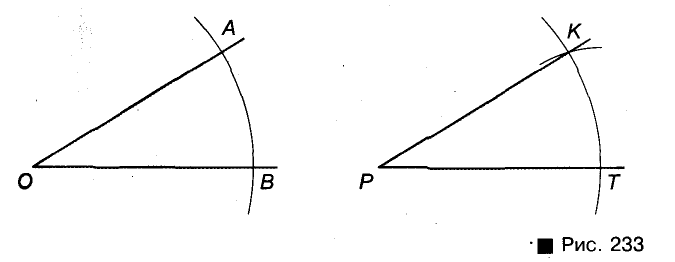
Постройте угол, равный данному углу.
Решение:
Пусть дан угол АОВ и требуется построить угол КРТ, равный 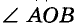
который требовалось построить. Ведь треугольники КРТ и АОВ равны (по трем сторонам), поэтому
Пример №8
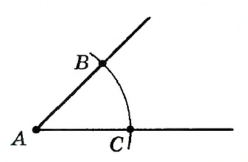
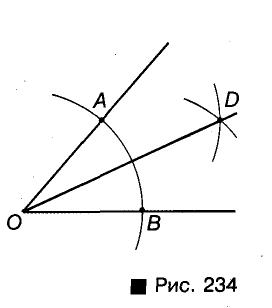
Постройте биссектрису данного угла.
Решение:
Пусть АОВ — данный угол (рис. 234). Произвольным раствором циркуля опишем дугу с центром О. Пусть А и В — точки пересечения этой дуги с лучами О А и ОВ. Из центров А и В опишем дуги такими же радиусами. Если D — точка пересечения этих дуг, то луч OD — биссектриса угла АОВ.
Действительно, 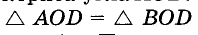
Пример №9
Разделите данный отрезок пополам.
Решение:
Пусть АВ — данный отрезок (рис. 235). Из точек А и В радиусом АВ описываем дуги. Они пересекутся в неких точках С и D.
Прямая CD точкой М разделит данный отрезок пополам.
Действительно, по трем сторонам 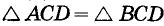
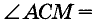
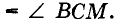
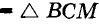
Пример №10
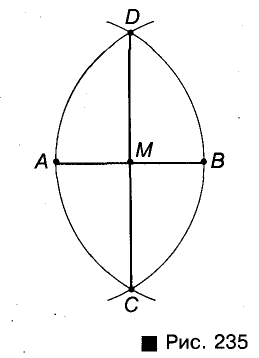
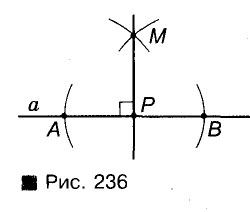
Через данную точку Р проведите прямую, перпендикулярную и данной прямой а.
Решение:
В зависимости от того, лежит или не лежит точка Р на прямой а, задачу можно решить, как показа но на рисунках 236 и 237. Опишите и аргументируйте эти построения самостоятельно.
Пример №11
Через точку Р, не лежащую на прямой АВ, проведите прямую, параллельную прямой АВ.
Решение:
Через точку Р и про из вольную точку А прямой АВ проводим прямую АТ (рис. 238). Строим угол ТРМ, равный углу РАВ, так, что бы эти углы стали соответственны ми при прямых РК, АВ и секущей АР. Построенная таким образом пря мая РК удовлетворяет задачу: она проходит через данную точку Р и параллельна прямой АВ, поскольку
Геометрическими построениями часто приходилось заниматься многим людям. Еще в доисторические времена мастера, изготавливающие колеса к колесницам, умели делить окружность на несколько равных частей. В наше время выполнять такие построения приходится специалистам, проектирующим или изготавливающим шестеренки, дисковые пилы (рис. 239), турбины и различные роторные механизмы. Как бы вы разделили окружность, например, на 5, 6 или 7 равных частей?
Основные чертежные инструменты — линейка и циркуль — были известны еще несколько тысячелетий назад.
Слово линейка происходит от слова линия, которое на латинском языке сначала означало «льняная нитка», «черта, проведенная ниткой, бечевкой» (производное от лат. Плит — лен). Слово циркуль тоже латинского происхождения, первоначально слово циркулюс означало «окружность, круг», а потом стало означать инструмент, с помощью которого проводят окружности.
В Древней Греции линейку и циркуль признавали единственными приборами геометрических построений. Задачу на построение считали решенной, если все построения в ней выполнялись только с помощью линейки и циркуля. Сейчас специалисты при выполнении построений пользуются угольником, транспортиром, рейсмусом, рейсшиной и другими чертежными приспособлениями.
Пример №12
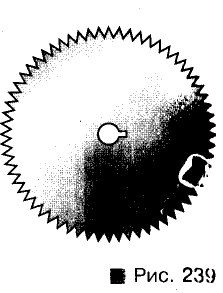
Разделите данную дугу окружности на две равные части.
Решение:
Пусть дана дуга АВ окружности с центром О (рис. 240). Представим угол АОВ и проведем его биссектрису ОК. Треугольники АОК и КОВ равны, поэтому и дуги АК и КВ равны.
Пример №13
Постройте угол вдвое больше данною.
Решение:
Пусть АОВ — данный угол (рис. 241) Опишем дугу окружности с центром О Если она пересечет стороны данного угла в точках А и В, из В как из центра сделаем засечку ВС = ВА и проведем луч ОС. Угол АОС вдвое больше
Задачи на построение
С геометрическими построениями имеют дело различные специалисты. Геометрические построении выполняют чертежники, архитекторы, конструкторы, топографы, геодезисты, штурманы. Разные геометрические фигуры строят также: слесарь — на жести, столяр — на доске, портной— на ткани, садовник — на земле.
В задаче на построение требуется построить геометрическую фигуру, которая должна удовлетворять определенные условия. В геометрии построения выполняют чаще всего с помощь к линейки и циркуля. Условимся: если в задаче не сказано, какими инструментами следует выполнить построение, то имеются в виду только линейка (без делений) и циркуль.
Более сложные задачи на построение часто решают методом геометрических мест. Пусть, например, в задаче требуете!’ найти точку X, удовлетворяющую два условия. Если первое условие удовлетворяют точки фигуры К, а второе — точки фигуры Р, то X должна принадлежать каждой из этих фигур. Тс есть X — точка пересечения фигур К и Р.
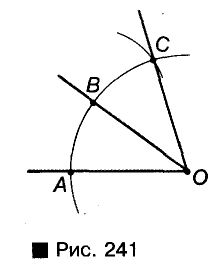
Пример №14
Постройте прямоугольный треугольник по да» ному катету а и гипотенузе с (рис. 243).
Решение:
Строим прямой угол АСВ, на его стороне откладываем отрезок СВ = а. Точки С и В — две вершины треугольника, который требуется построить. Третья верши» должна лежать, во-первых, на луче СА, во-вторых, на pfti стоянии с от В, то есть на окружности радиуса с с центр В. Если эту окружность пересекает луч СА в точке А, 1 треугольник ABC — именно тот, который требовалось не строить. Ведь его угол С прямой, ВС = а, ВА = с.
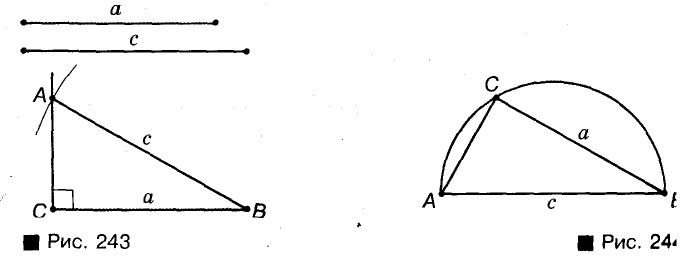
Второй способ (рис. 244). Откладываем отрезок АВ = с и проводим окружность диаметра АВ — ГМТ, из которых АВ виден под прямым углом. Дальше строим полуокружность радиуса а с центром В — ГМТ, удаленных от В на расстояние а и лежащих по одну сторону от прямой АВ. Если два ГМТ пересекаются в точке С, то треугольник ABC — именно тот, который требовалось построить.
Составные части решения задачи на построение — анализ, построение, доказательство и исследование. В анализе ищут способ решения задачи, в построении выполняется само построение, в доказательстве обосновывается правильность выполненного построения, в исследовании выясняется, сколько решений имеет задача.
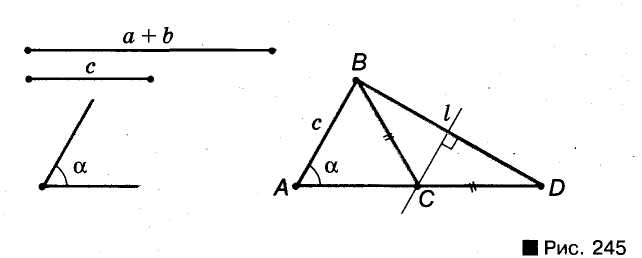
Пример №15
Постройте треугольник по данной стороне, прилежащему к ней углу и сумме двух других сторон (рис. 245).
Решение:
Анализ. Допустим, что требуемый треугольник ABC построен. Его сторона с и угол А = а — даны. Дан также отрезок, равный сумме сторон а и b. По данным отрезкам с и а + b и углу А между ними можно построить A ABD. Вершиной С искомого треугольника будет такая точка отрезка AD, для которой CD = СВ. Следовательно, точка С должна лежать и на серединном перпендикуляре отрезка BD.
Построение. По двум данным отрезкам и углу между ними строим 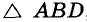
Доказательство:
В треугольнике 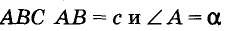
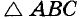
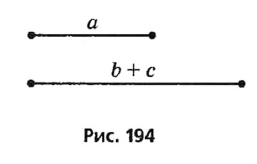
Исследование. Задача имеет решение только при условии, что а + b > с.
Если задача несложная и способ ее решения известен, анализ можно не описывать. А в решении не обязательно выделять анализ, построение, доказательство и исследование.
В математике чаще всего имеют дело с задачами: на вычисление, на доказательство, на построение, на преобразование и на исследование. Геометрическими задачами на построение активно интересовались античные геометры. Допуская лишь классические построения (выполняемые только линейкой и циркулем), они исследовали, какие из построений можно вы-полнить, а какие невозможно. В частности, выясняли:
- можно ли любой угол разделить на три равные части;
- можно ли построить квадрат, площадь которого была бы равна площади данного круга;
- можно ли построить ребро такого куба, объем которого был бы в 2 раза больше объема данного куба.
Много столетий выдающиеся геометры пытались решить эти задачи и не смогли. Эти три классические задачи древности получили специальные названия:
- трисекция угла,
- 2квадратура круга,
- удвоение куба.
Последнюю задачу называют еще делосской задачей, связывая ее с древнегреческой легендой. согласно которой оракул бога Аполлона согласился спасти жителей острова Делос от чумы, если кубический жертовник в делосском храме заменят на жертовник такой же формы, но вдвое большего объема. Только почти через 2000 лет ученые убедились, что ни одну из этих трех задач с помощью лишь линейки и циркуля решить невозможно.
В настоящее время специалисты, которым приходится выполнять геометрические построения, пользуются не только линейкой и циркулем. С точки зрения классических методов такие построения приближенные. Но для практических нужд точности, которую обеспечивают приближенные методы, вполне достаточно
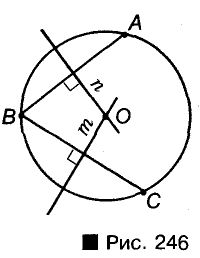
Пример №16
Найдите центр данной окружности.
Решение:
Обозначим на данной окружности три производные точки А, В и С (рис. 246).
Представим хорды АВ, ВС и проведем их серединные перпендикуляры n и m. Точка О, в которой пересекаются прямые n и m., — центр данной окружности. Ведь ОА = ОВ = ОС.
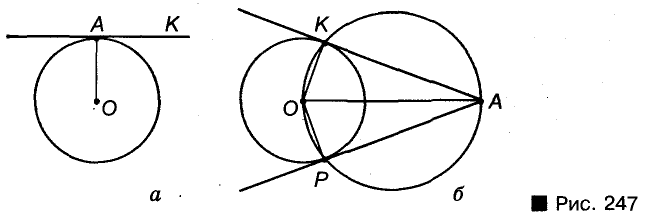
Пример №17
Через данную точку проведите касательную к данной окружности.
Решение:
Если данная точка А лежит на окружности центра О (рис. 247, а), проводим луч ОА, потом — прямую АК, перпендикулярную к ОА. Прямая АК — касательная, которую и требовалось построить.
Если точка А лежит вне данной окружности центра О (рис. 247, б), то на диаметре ОА описываем окружность. Она пересечется с данной окружностью в двух точках К и Р. Прямые АК и АР — искомые касательные, поскольку 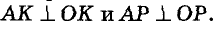
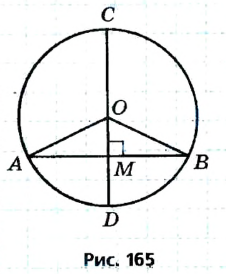
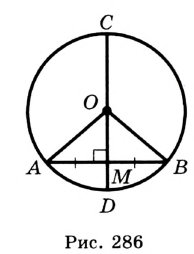
Свойство диаметра, перпендикулярного хорде
Диаметр, перпендикулярный хорде, проходит через ее середину. Докажите.
Решение
Пусть СО — диаметр окружности с центром О, АВ — хорда этой окружности, 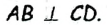
В случае, когда хорда АВ сама является диаметром, точка М совпадает с центром О и утверждение задачи очевидно. Пусть хорда АВ не является диаметром (рис. 165). Проведем радиусы OA и ОВ. Тогда в равнобедренном треугольнике АОВ высота ОМ является медианой. Итак, AM = ВМ, что и требовалось доказать.
Докажите самостоятельно еще одно утверждение (опорное): диаметр окружности, проведенной через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
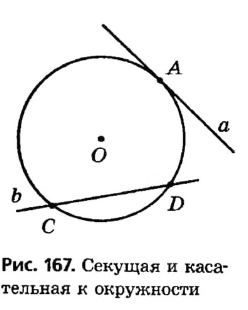
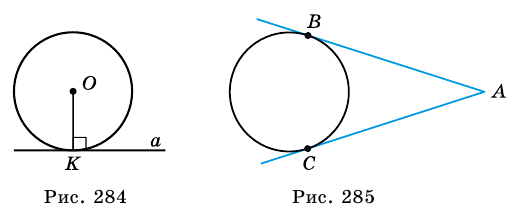
Касательная к окружности
Определение и свойство касательной
Любая прямая, проходящая через точки окружности, называется секущей; ее отрезок, лежащий внутри окружности, является хордой. На рисунке 167 хорда CD — отрезок секущей b . Рассмотрим теперь прямую, имеющую с окружностью только одну общую точку.
Определение:
Касательной к окружности называется прямая, имеющая с окружностью единственную общую точку. Общая точка касательной и окружности называется точкой касания.
На рисунке 167 прямая а является касательной к окружности с центром О. Иначе говоря, прямая а касается окружности с центром О в точке А .
Определим взаимное расположение касательной и радиуса окружности, проведенного в точку касания.
Теорема (свойство касательной)
Касательная к окружности перпендикулярна радиусу, проведенному в точку касания.
Доказательство:
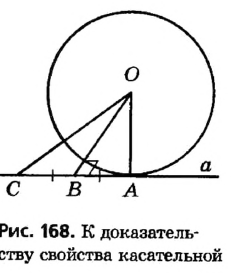
Пусть прямая а касается окружности с центром О в точке А (рис. 168). Докажем, что 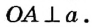
Пусть отрезок OA не является перпендикуляром к прямой а. Тогда, по теореме о существовании и единственности перпендикуляра к прямой, из точки О можно провести перпендикуляр ОB к прямой а . На луче АВ от точки В отложим отрезок ВС, равный АВ , и соединим точки О и С . Поскольку по построению отрезок ОВ — медиана и высота треугольника АОС, то этот треугольник равнобедренный с основанием АС, то есть OA = ОС . Таким образом, расстояние между точками О и С равно радиусу окружности, и, по определению радиуса, точка С должна лежать на данной окружности. Но это противоречит определению касательной, поскольку А — единственная общая точка окружности с прямой а. Из этого противоречия следует, что наше предположение неверно, то есть OA 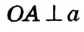
Признак касательной
Докажем теорему, обратную предыдущей.
Теорема: (признак касательной)
Если прямая проходит через точку окружности перпендикулярно радиусу, проведенному в эту точку, то она является касательной к окружности.
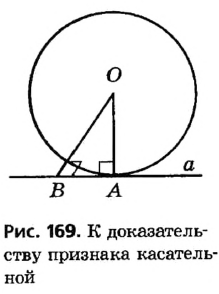
Доказательство:
Пусть прямая а проходит через точку А, лежащую на окружности с центром О, причем 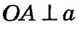
Пусть прямая а имеет с окружностью общую точку В , отличную от А (рис. 169). Тогда из определения окружности ОА = ОВ как радиусы, то есть треугольник АОВ равнобедренный с основанием АВ. По свойству углов равнобедренного треугольника 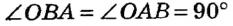
Следовательно, точка А — единственная общая точка окружности и прямой а, значит, прямая а — касательная к окружности.
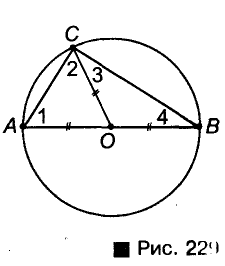
Свойство отрезков касательных
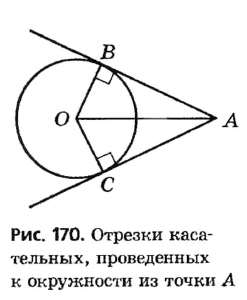
Пусть даны окружность с центром О и точка А, не принадлежащая кругу, ограниченному данной окружностью (рис. 170).
Через точку А можно провести две касательные к данной окружности. Отрезки, соединяющие данную точку А с точками касания, называют отрезками касательных, проведенных из точки А к данной окружности. На рисунке 170 АВ и АС — отрезки касательных, проведенных к окружности из точки А .
Опорная задача
Отрезки касательных, проведенных из данной точки к окружности, равны. Докажите.
Решение
Пусть АВ и АС — отрезки касательных, проведенных к окружности с центром О из точки А (рис. 170). Рассмотрим треугольники АОВ и АОС. По свойству касательной 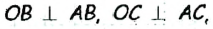
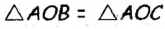
Касание двух окружностей
Определение:
Две окружности, имеющие общую точку, касаются в этой точке, если они имеют в ней общую касательную.
Общая точка двух окружностей в таком случае называется точкой касания окружностей.
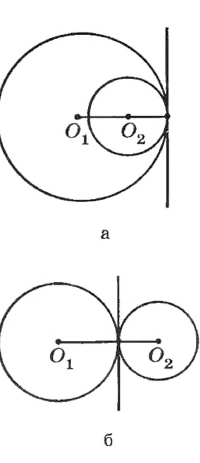
Различают два вида касания окружностей: внутреннее и внешнее.
Касание окружностей называется внутренним, если центры окружностей лежат по одну сторону от общей касательной, проведенной через точку касания (рис. 171, а);
Касание окружностей называется внешним, если центры окружностей лежат по разные стороны от общей касательной, проведенной через точку касания (рис. 171, б).
Рис. 171 Касание двух окружностей. 1. внутреннее; 2. внешнее.
По свойству касательной радиусы данных окружностей, проведенные в точку касания, перпендикулярны общей касательной. Из теоремы о существовании и единственности прямой, перпендикулярной данной, следует, что центры касающихся окружностей и точка касания окружнос тей лежат на одной прямой.
Касающиеся окружности имеют единствен ную общую точку — точку касания.
Если данные окружности имеют радиусы R и r (R > r), то расстояние между центрами окружностей равно R-r в случае внутреннего касания и R+r в случае внешнего касания.
Задачи на построение
Что такое задачи на построение?
Задачи на построение представляют собой отдельный класс геометрических задач, решение которых подчиняется определенным правилам. Цель решения этих задач — построение геометрических фигур с заданными свойствами с помощью чертежных инструментов. Если в условии задачи нет специальных примечаний, то имеются в виду построения с помощью циркуля и линейки. С помощью линейки можно провести:
- произвольную прямую;
- прямую, проходящую через данную точку;
- прямую, проходящую через две данные точки.
Заметим, что никаких других построений линейкой выполнять нельзя. В частности, с помощью линейки нельзя откладывать отрезки заданной длины.
Циркуль — от латинского «циркулус» — окружность, круг.
С помощью циркуля можно:
- провести окружность (часть окружности) произвольного или заданного радиуса с произвольным или заданным центром;
- отложить от начала данного луча отрезок заданной длины.
Кроме того, можно отмечать на плоскости точки и находить точки пересечения прямых и окружностей.
Все перечисленные операции называют элементарными построениями, а решить задачу на построение — это значит найти последовательность элементарных построений, после выполнения которых искомая фигура считается построенной, и доказать, что именно эта фигура удовлетворяет условию задачи.
Итак, решение задач на построение заключается не столько в самом построении фигуры, сколько в нахождении способа построения и доказательстве того, что полученная фигура искомая.
Основные задачи на построение
Если каждый шаг построений описывать полностью, решение некоторых задач может оказаться довольно громоздким. С целью упрощения работы выделяют несколько важнейших задач, которые считаются основными и не детализируются каждый раз при решении более сложных задач.
| Построение треугольника с данными сторонами | |||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||
| Построение биссектрисы угла | |
 | Пусть дан неразвернутый угол с вершиной А . Построим его биссектрису. |
 | С помощью циркуля построим окружность произвольного радиуса с центром А . Пусть В к С — точки пересечения этой окружности со сторонами данного угла. |
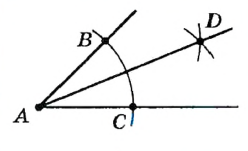 | Построим окружности того же радиуса с центрами В и С . Пусть D — точка пересечения этих окружностей. |
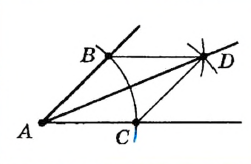 | Проведем луч AD. По построению 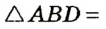 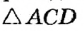 (по третьему признаку). Отсюда (по третьему признаку). Отсюда  , то есть AD — биссектриса данного угла А . , то есть AD — биссектриса данного угла А . |
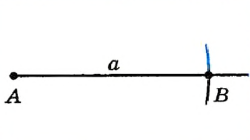
| Построение перпендикулярной прямой | |
 | Пусть даны прямая а и точка О . Построим прямую, проходящую через точку О и перпендикулярную прямой а . Рассмотрим два случая |
| Точка O лежит на прямой а | |
 | |
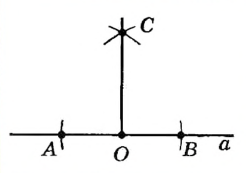 | Построим окружности радиуса АВ с центрами А и В. Пусть С — одна из точек их пересечения. Проведем прямую через точки С и О. |
 | По построению отрезок СО — медиана равностороннего треугольника ABC , которая является также его высотой. Итак,  , то есть прямая СО — искомая. , то есть прямая СО — искомая. |
| Точка O не лежит на прямой а | |
 | Построим окружность с центром О , которая пересекает прямую O, в точках А и В . |
 | Построими окружности того же радиуса с центрами A и В . Пусть Ol — точка пересечения этих окружностей, причем точки О и Ol лежат по разные стороны от прямой а . |
 | Проведем прямую 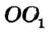 . Пусть С — точка пересечения прямых . Пусть С — точка пересечения прямых 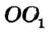 и а . По построению и а . По построению 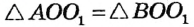 (по третьему признаку). Отсюда (по третьему признаку). Отсюда 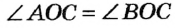 . Тогда ОС — биссектриса равнобедренного треугольника АОВ , проведенная к основанию. Она также является медианой и высотой треугольника. Следовательно, . Тогда ОС — биссектриса равнобедренного треугольника АОВ , проведенная к основанию. Она также является медианой и высотой треугольника. Следовательно, 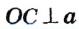 а , то есть прямая а , то есть прямая  — искомая. — искомая. |
Отметим, что построенная прямая 
Пользуясь описанными построениями, несложно решить задачи на построение середины данного отрезка и на построение прямой, параллельной данной.
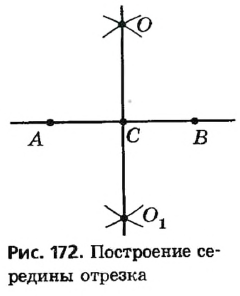
Для построения середины отрезка АВ достаточно провести две окружности радиуса АВ с центрами в точках А к В (рис. 172). Обозначив точки пересечения этих окружностей через 
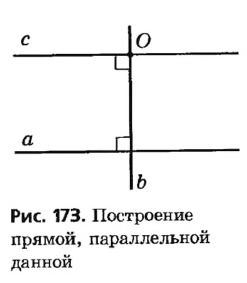
Для построения прямой, проходящей через данную точку О параллельно данной прямой а, достаточно провести через точку О прямую b , перпендикулярную а, и прямую с, перпендикулярную b (рис. 173). Тогда а || с по теореме о двух прямых, перпендикулярных третьей.
Таким образом, основными задачами на построение будем считать следующие:
- построение треугольника с данными сторонами;
- построение угла, равного данному неразвернутому углу;
- построение биссектрисы данного неразвернутого угла;
- построение прямой, проходящей через данную точку перпендикулярно данной прямой;
- построение серединного перпендикуляра к данному отрезку;
- построение середины данного отрезка;
- построение прямой, проходящей через данную точку параллельно данной прямой.
Если эти задачи применяются как вспомогательные при решение более сложных задач, соответствующие построения можно подробно не описывать.
Решение задач на построение
Решение задач на построение состоит из четырех основных этапов: анализ, построение, доказательство, исследование.
| Общая схема решения задач на построение | ||
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Описанные и вписанные окружности
- Плоские и пространственные фигуры
- Взаимное расположение точек и прямых
- Сравнение и измерение отрезков и углов
- Решение треугольников
- Треугольники и окружность
- Площадь треугольника
- Соотношения между сторонами и углами произвольного треугольника
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
💥 Видео
Найти центр кругаСкачать

Геометрия 8 класс (Урок№25 - Взаимное расположение прямой и окружности.)Скачать

Длина окружности. Площадь круга. 6 класс.Скачать

Части круга и окружности #егэпрофиль #егэ #профиль #умскул #профильнаяматематикаСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Найти центр и радиус окружностиСкачать

№160. Прямая а проходит через середину отрезка АВ и перпендикулярна к нему. Докажите, что: а) каждаяСкачать

№203. Через центр О окружности, вписанной в треугольник ABC, проведена прямая ОK, перпендикулярнаяСкачать

Теорема о числе точек пересечения двух окружностейСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

































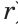
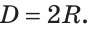



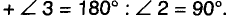
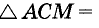
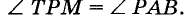
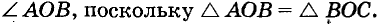
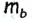 — две стороны и медиана треугольника ABC, который необходимо построить (рис. 174).
— две стороны и медиана треугольника ABC, который необходимо построить (рис. 174).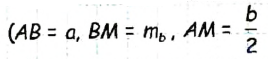 по условию задачи). Таким образом, мы можем построить треугольник АВМ и найти вершины А и В искомого треугольника. Чтобы найти вершину С, достаточно отложить на луче AM отрез ок МС длиной
по условию задачи). Таким образом, мы можем построить треугольник АВМ и найти вершины А и В искомого треугольника. Чтобы найти вершину С, достаточно отложить на луче AM отрез ок МС длиной 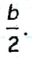
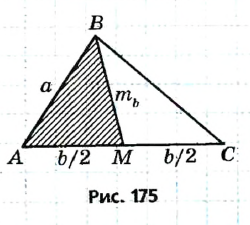
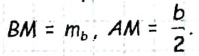
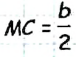 .
. — медиана (по построению). Следовательно, треугольник ABC искомый.
— медиана (по построению). Следовательно, треугольник ABC искомый. — удовлетворяют неравенству треугольника.
— удовлетворяют неравенству треугольника.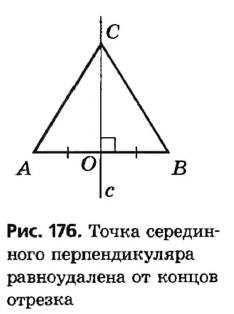
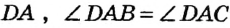 по условию. Тогда
по условию. Тогда 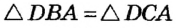 по гипотенузе и острому углу. Отсюда DB = DC , то есть точка D равноудалена от сторон данного угла.
по гипотенузе и острому углу. Отсюда DB = DC , то есть точка D равноудалена от сторон данного угла.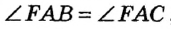 , то есть луч AF — биссектриса угла А.
, то есть луч AF — биссектриса угла А.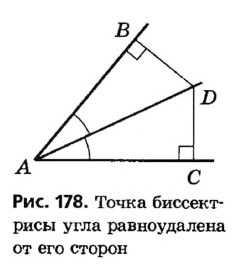
 и
и  . Если геометрическим местом точек, удовлетворяющих условию
. Если геометрическим местом точек, удовлетворяющих условию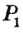 , является фигура
, является фигура 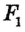 , а геометрическим местом точек, удовлетворяющих условию
, а геометрическим местом точек, удовлетворяющих условию 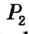 — фигура
— фигура 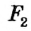 то искомая точка будет общей для фигур
то искомая точка будет общей для фигур  с.
с.
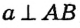 , то
, то 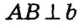 по следствию из теоремы о свойствах углов при параллельных прямых. Но
по следствию из теоремы о свойствах углов при параллельных прямых. Но 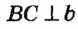 по построению, отсюда
по построению, отсюда 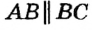 что невозможно по условию. Следовательно, прямые а и b пересекаются в некоторой точке О.
что невозможно по условию. Следовательно, прямые а и b пересекаются в некоторой точке О.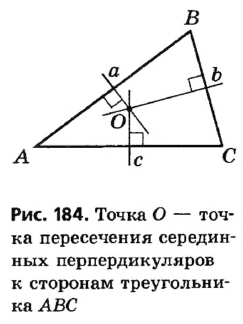
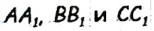 являются также медианами и высотами (рис. 188). Это означает, что. прямые
являются также медианами и высотами (рис. 188). Это означает, что. прямые  — серединные перпендикуляры к сторонам треугольника ABC. Поскольку все они пересекаются в одной точке, то эта точка — центр описанной и вписанной окружностей треугольника ABC.
— серединные перпендикуляры к сторонам треугольника ABC. Поскольку все они пересекаются в одной точке, то эта точка — центр описанной и вписанной окружностей треугольника ABC.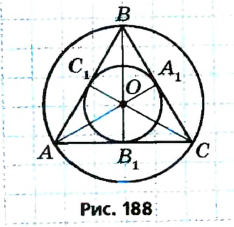
 по построению. В треугольнике
по построению. В треугольнике  — высота и медиана (по построению). Значит, треугольник АСD равнобедренный с основанием AD), откуда СА=СD=с. По построению
— высота и медиана (по построению). Значит, треугольник АСD равнобедренный с основанием AD), откуда СА=СD=с. По построению  , следовательно,
, следовательно, 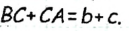 Таким образом, треугольник ABC искомый.
Таким образом, треугольник ABC искомый.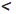 c+b
c+b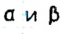 — углы, на которые медиана делит угол треугольника (рис. 196).
— углы, на которые медиана делит угол треугольника (рис. 196).
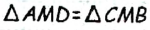 (АМ=СМ по определению медианы, ВМ =DМ по построению,
(АМ=СМ по определению медианы, ВМ =DМ по построению, 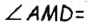
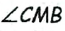 как вертикальные). Тогда
как вертикальные). Тогда 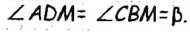
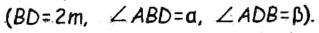 Построив этот треугольник, получим вершины А и В скомого треугольника. Для построения вершины С достаточно удвоить в треугольнике АВD медиану AM.
Построив этот треугольник, получим вершины А и В скомого треугольника. Для построения вершины С достаточно удвоить в треугольнике АВD медиану AM.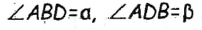 . Треугольник АВй вспомогательный.
. Треугольник АВй вспомогательный.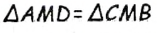 по первому признаку равенства треугольников
по первому признаку равенства треугольников 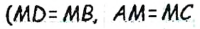 по построению,
по построению, 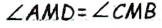 как вертикальные). Тогда
как вертикальные). Тогда 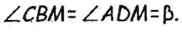 Также по построению
Также по построению 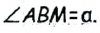 В треугольнике
В треугольнике 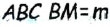 — медиана, поскольку по построению
— медиана, поскольку по построению 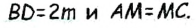 Таким образом, треугольник ABC — искомый.
Таким образом, треугольник ABC — искомый.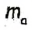 — проведенная к ней медиана,
— проведенная к ней медиана, 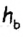 — высота треугольника, проведенная к другой стороне (рис. 198). Построим этот треугольник.
— высота треугольника, проведенная к другой стороне (рис. 198). Построим этот треугольник.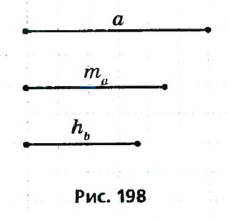
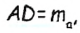 то точка А должна лежать на расстоянии
то точка А должна лежать на расстоянии 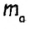 от точки D. Это означает, что A — точка пересечения прямой СH и окружности радиуса
от точки D. Это означает, что A — точка пересечения прямой СH и окружности радиуса 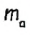 с центром D.
с центром D.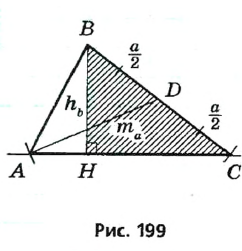
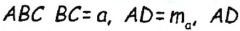 — медиана,
— медиана, 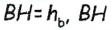 — высота (по построению). Следовательно, треугольник ABC — искомый.
— высота (по построению). Следовательно, треугольник ABC — искомый.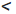 a. В зависимости от длины медианы
a. В зависимости от длины медианы 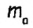 задача имеет одно или два решения, или не имеет ни одного.
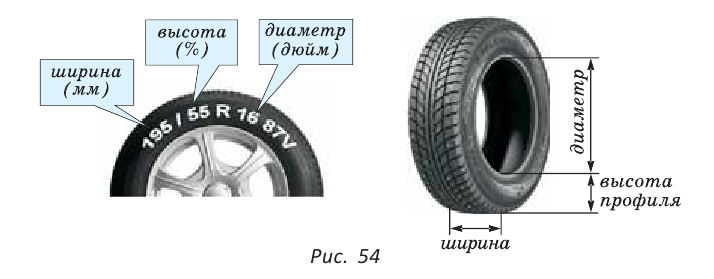
задача имеет одно или два решения, или не имеет ни одного.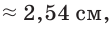 то для нашей шины получим
то для нашей шины получим 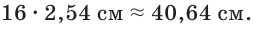

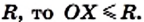
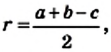 где r — радиус вписанной окружности, а и b — катеты, с — гипотенуза.
где r — радиус вписанной окружности, а и b — катеты, с — гипотенуза.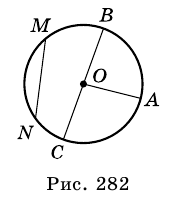
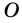 — центр окружности,
— центр окружности, 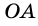 — радиус окружности.
— радиус окружности.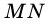 — хорда,
— хорда, 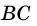 — диаметр. Часть плоскости, ограниченную окружностью, вместе с самой окружностью называют кругом (рис. 283).
— диаметр. Часть плоскости, ограниченную окружностью, вместе с самой окружностью называют кругом (рис. 283).
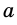 — касательная к окружности, точка
— касательная к окружности, точка  — точка касания.
— точка касания.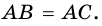

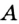 и
и  . Для всех точек зададим свойство: одновременно принадлежать лучам
. Для всех точек зададим свойство: одновременно принадлежать лучам  и
и 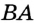 . Ясно, что указанным свойством обладают все точки отрезка
. Ясно, что указанным свойством обладают все точки отрезка 
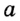 и
и 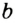 . Для всех точек зададим свойство: принадлежать прямой
. Для всех точек зададим свойство: принадлежать прямой 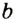 и находиться на расстоянии 1 см от прямой
и находиться на расстоянии 1 см от прямой  и
и  (рис. 274) удовлетворяют этим условиям. Также понятно, что никакая другая точка, отличная от
(рис. 274) удовлетворяют этим условиям. Также понятно, что никакая другая точка, отличная от  , этим свойством не обладает. Следовательно, искомое ГМТ — это фигура, состоящая из двух точек
, этим свойством не обладает. Следовательно, искомое ГМТ — это фигура, состоящая из двух точек 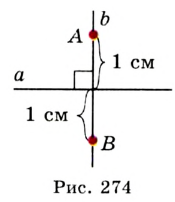
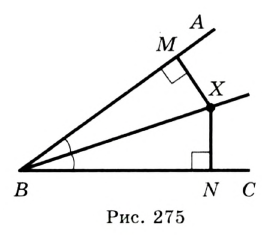
 не совпадает с вершиной угла
не совпадает с вершиной угла  и принадлежит его биссектрисе (рис. 275). Опустим перпендикуляры
и принадлежит его биссектрисе (рис. 275). Опустим перпендикуляры  и
и 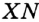 соответственно на стороны
соответственно на стороны 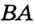 и
и 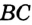 . Надо доказать, что
. Надо доказать, что 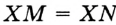 .
.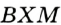 и
и 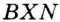 гипотенуза
гипотенуза 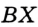 — общая,
— общая, 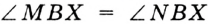 , так как
, так как 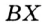 — биссектриса угла
— биссектриса угла 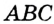 . Следовательно,
. Следовательно, 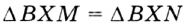 по гипотенузе и острому углу. Отсюда
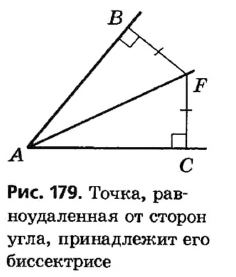
по гипотенузе и острому углу. Отсюда  . Обратная теорема. Если точка, принадлежащая углу, равноудалена от его сторон, то она лежит на биссектрисе этого угла.
. Обратная теорема. Если точка, принадлежащая углу, равноудалена от его сторон, то она лежит на биссектрисе этого угла.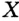 , принадлежащая углу
, принадлежащая углу 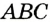 , не совпадает с его вершиной и равноудалена от его сторон. Опустим перпендикуляры
, не совпадает с его вершиной и равноудалена от его сторон. Опустим перпендикуляры 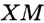 и
и 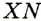 соответственно на стороны
соответственно на стороны 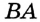 и
и 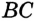 . Надо доказать, что
. Надо доказать, что  (рис. 275).
(рис. 275).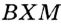 и
и 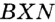 гипотенуза
гипотенуза 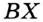 — общая,
— общая, 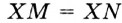 по условию. Следовательно,
по условию. Следовательно, 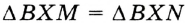 по гипотенузе и катету. Отсюда
по гипотенузе и катету. Отсюда 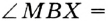
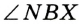 .
.
 или
или  принадлежит продолжению стороны угла (рис. 276). Исследовать эту ситуацию вы можете на занятии математического кружка. Также отметим, что теорема остается справедливой и для развернутого угла.
принадлежит продолжению стороны угла (рис. 276). Исследовать эту ситуацию вы можете на занятии математического кружка. Также отметим, что теорема остается справедливой и для развернутого угла.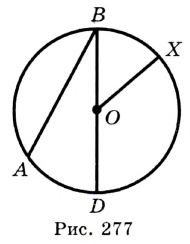
 — центр окружности.
— центр окружности. — радиус. Из определения следует, что все радиусы одной окружности равны.
— радиус. Из определения следует, что все радиусы одной окружности равны. — хорда. Хорду, проходящую через центр окружности, называют диаметром. На рисунке 277 отрезок
— хорда. Хорду, проходящую через центр окружности, называют диаметром. На рисунке 277 отрезок 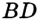 — диаметр окружности. Очевидно, что
— диаметр окружности. Очевидно, что 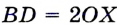 , т. е. диаметр окружности в два раза больше ее радиуса.
, т. е. диаметр окружности в два раза больше ее радиуса.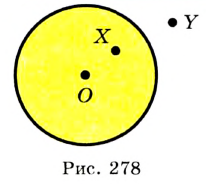
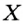 — произвольная точка круга с центром
— произвольная точка круга с центром 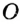 радиуса
радиуса 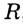 , то
, то 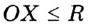 (рис. 278). Если
(рис. 278). Если 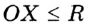 , то говорят, что точка
, то говорят, что точка  кругу не принадлежит (рис. 278). Также говорят, что точка
кругу не принадлежит (рис. 278). Также говорят, что точка  лежит вне окружности, ограничивающей круг. Из определения круга следует, что окружность, ограничивающая круг, ему принадлежит.
лежит вне окружности, ограничивающей круг. Из определения круга следует, что окружность, ограничивающая круг, ему принадлежит.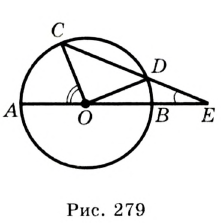
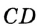 окружности с центром
окружности с центром 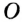 за точку
за точку 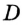 отметили точку
отметили точку 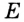 такую, что отрезок
такую, что отрезок 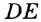 равен радиусу окружности (рис. 279). Прямая
равен радиусу окружности (рис. 279). Прямая 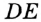 пересекает данную окружность в точках
пересекает данную окружность в точках  и
и  . Докажите, что
. Докажите, что 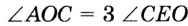 .
.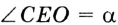 . Так как
. Так как 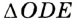 — равнобедренный, то
— равнобедренный, то 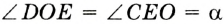 .
. 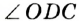 — внешний угол треугольника
— внешний угол треугольника 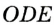 ,
, 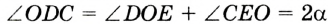 . Так как
. Так как  — равнобедренный, то имеем:
— равнобедренный, то имеем: 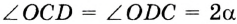 .
. 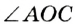 — внешний угол треугольника
— внешний угол треугольника 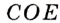 . Тогда
. Тогда 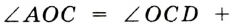
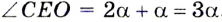 , то есть
, то есть 
 .
.
 ,
, 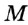 — точка пересечения диаметра
— точка пересечения диаметра 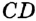 и хорды
и хорды 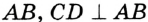 . Надо доказать, что
. Надо доказать, что 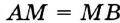 . Проведем радиусы
. Проведем радиусы 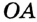 и
и 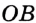 . В равнобедренном треугольнике
. В равнобедренном треугольнике 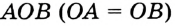 отрезок
отрезок  — высота, а значит, и медиана, т. е.
— высота, а значит, и медиана, т. е.  .
.
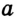 — касательная,
— касательная,  — точка касания.
— точка касания.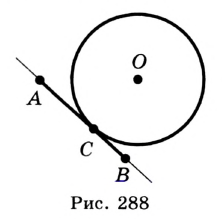
 , который касается окружности в точке
, который касается окружности в точке  .
.
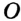 ,
, 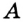 — точка касания прямой
— точка касания прямой 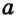 и окружности. Надо доказать, что
и окружности. Надо доказать, что 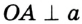 .
.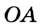 — наклонная к прямой
— наклонная к прямой 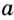 . Тогда из точки
. Тогда из точки 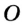 опустим перпендикуляр
опустим перпендикуляр 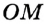 на прямую
на прямую 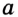 (рис. 289). Поскольку точка
(рис. 289). Поскольку точка 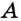 — единственная общая точка прямой а и круга с центром
— единственная общая точка прямой а и круга с центром 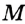 не принадлежит этому кругу. Отсюда
не принадлежит этому кругу. Отсюда 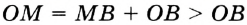
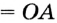 . Получили противоречие: перпендикуляр
. Получили противоречие: перпендикуляр 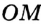 больше наклонной
больше наклонной 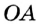 . Следовательно,
. Следовательно, 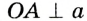 .
.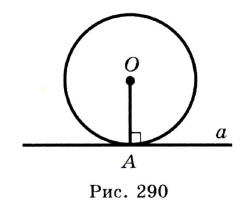
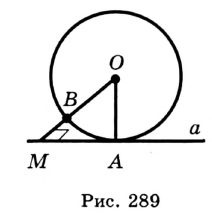
 , отрезок
, отрезок  — ее радиус, точка
— ее радиус, точка  принадлежит прямой
принадлежит прямой 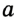 ,
, 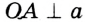 . Докажем, что прямая
. Докажем, что прямая 
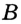 с окружностью (рис. 291). Тогда
с окружностью (рис. 291). Тогда 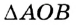 — равнобедренный (
— равнобедренный ( 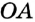 и
и 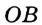 равны как радиусы). Отсюда получаем противоречие: в треугольнике
равны как радиусы). Отсюда получаем противоречие: в треугольнике 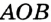 есть два прямых угла. Следовательно, прямая
есть два прямых угла. Следовательно, прямая 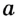 является касательной к окружности. Следствие. Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.
является касательной к окружности. Следствие. Если расстояние от центра окружности до некоторой прямой равно радиусу окружности, то эта прямая является касательной к данной окружности.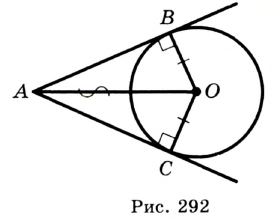
 . Прямые
. Прямые  и
и 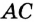 — касательные,
— касательные,  и
и  — точки касания. Надо доказать, что
— точки касания. Надо доказать, что 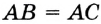 . Проведем радиусы
. Проведем радиусы 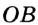 и
и 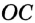 в точки касания. По свойству касательной
в точки касания. По свойству касательной 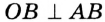 и
и 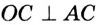 . В прямоугольных треугольниках
. В прямоугольных треугольниках 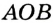 и
и 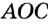 катеты
катеты 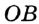 и
и 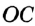 равны как радиусы одной окружности,
равны как радиусы одной окружности, 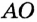 — общая гипотенуза. Следовательно,
— общая гипотенуза. Следовательно, 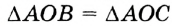 по гипотенузе и катету. Отсюда
по гипотенузе и катету. Отсюда 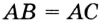 .
.