- Призма
- Формулы вычисления объема и площади поверхности призмы:
- В основании лежит треугольник.
- В основании лежит четырехугольник
- 1. Прямоугольник
- 2. Ромб
- 3. Трапеция
- Рассмотрим площади правильных многоугольников:
- Подобие треугольников
- Прямоугольный треугольник и его свойства:
- Теорема Пифагора
- Теорема синусов
- Теорема косинусов
- Прямая призма прямоугольный треугольник
- Что это — прямая призма? Свойства и формулы. Пример задачи
- Призма и ее виды
- Что это — призма прямая?
- Объем прямой призмы
- Площадь боковой поверхности
- Задача с треугольной призмой
- 📹 Видео
Видео:№234. Основанием прямой призмы является прямоугольный треугольник. Через середину гипотенузыСкачать

Призма
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.
Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
$P_$ — периметр основания;
$S_$ — площадь основания;
$S_$ — площадь боковой поверхности;
$S_$ — площадь полной поверхности;
$h$ — высота призмы.
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/$, где $h_a$ — высота, проведенная к стороне $а$
- $S=/$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√
$, где $р$ — это полупериметр $p=/$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S=/$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S=/$, где $а$ и $b$ — катеты прямоугольного треугольника.
В основании лежит четырехугольник
1. Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб
$S=/$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция
$S=/$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
1. Для равностороннего треугольника $S=/$, где $а$ — длина стороны.
$S=a^2$, где $а$ — сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
Цилиндр — это та же призма, в основании которой лежит круг.
Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.
Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $/$ | $/$ | $/$ |
| $cosα$ | $/$ | $/$ | $/$ |
| $tgα$ | $/$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $/$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Видео:🔴 В основании прямой призмы лежит прямоугольный ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Прямая призма прямоугольный треугольник
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 7, боковое ребро равно 4. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 6, боковое ребро равно 6. Найдите объем призмы.
Объем прямой призмы равен где S — площадь основания, а h — ее боковое ребро. Тогда:
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 6, боковое ребро равно 6. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 4. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 4, боковое ребро равно 6. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 6, боковое ребро равно 5. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 8, боковое ребро равно 5. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 8, боковое ребро равно 6. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 7 и 8, боковое ребро равно 5. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 5, боковое ребро равно 6. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 5, боковое ребро равно 6. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 7, боковое ребро равно 6. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5, боковое ребро равно 4. Найдите объем призмы.
Это задание ещё не решено, приводим решение прототипа.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Объем прямой призмы равен где S – площадь основания, а h – боковое ребро. Тогда объем равен
Видео:№233. Основанием прямой призмы АВСA1B1C1 является прямоугольный треугольник ABCСкачать

Что это — прямая призма? Свойства и формулы. Пример задачи
Изучением характеристик трехмерных геометрических фигур занимается стереометрия. Одна из известных объемных фигур, которая появляется в задачах по геометрии, — это прямая призма. Рассмотрим в данной статье, что она собой представляет, а также подробно охарактеризуем призму с треугольным основанием.
Видео:🔴 В основании прямой призмы лежит ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 16 | ШКОЛА ПИФАГОРАСкачать

Призма и ее виды
Под призмой подразумевают такую фигуру, которая образуется в результате параллельного переноса многоугольника в пространстве. В результате этой геометрической операции образуется фигура, состоящая из нескольких параллелограммов и двух одинаковых параллельных друг другу многоугольников. Параллелограммы являются боковыми сторонами призмы, а многоугольники — это ее основания.

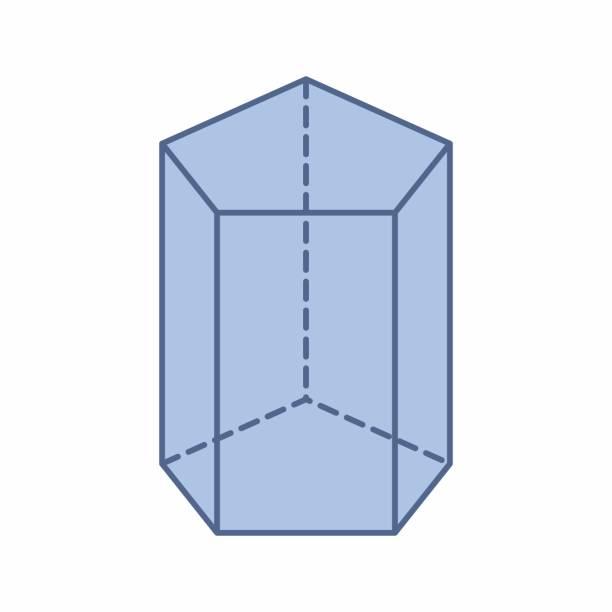
Любая призма имеет n+2 стороны, 3*n ребер и 2*n вершин, где n — число углов или сторон многоугольного основания. На изображении показана пятиугольная призма, которая состоит из 7 сторон, 10 вершин и 15 ребер.
Рассматриваемый класс фигур представлен призмами нескольких видов. Перечислим их кратко:
- вогнутые и выпуклые;
- наклонные и прямые;
- неправильные и правильные.
Каждая фигура относится к одному из перечисленных трех видов классификации. Во время решения геометрических задач проще всего выполнять расчеты для правильных и прямых призм. Последние подробнее рассмотрим в следующих пунктах статьи.
Видео:В основании прямой призмы лежит прямоугольный треугольник с катетами 5 и 6. Боковые ребра призмы...Скачать

Что это — призма прямая?
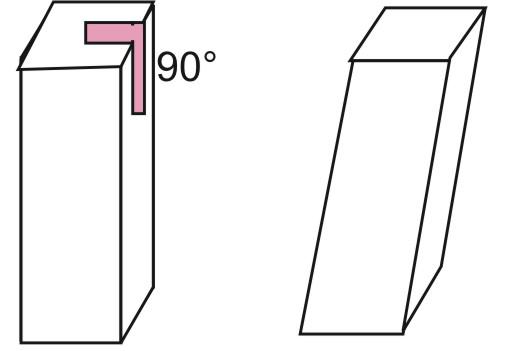
Прямой называется вогнутая или выпуклая, правильная или неправильная призма, у которой все боковые стороны представлены четырехугольниками с углами 90°. Если хотя бы один из четырехугольников боковых сторон не будет прямоугольником или квадратом, то призма называется наклонной. Можно также дать другое определение: прямая призма — это такая фигура данного класса, у которой любое боковое ребро равно высоте. Под высотой h призмы полагают дистанцию между ее основаниями.
Оба приведенных определения того, что это — прямая призма, являются равноправными и самодостаточными. Из них следует, что все двугранные углы между любым из оснований и каждой боковой стороной равны 90°.
Выше было сказано, что с прямыми фигурами удобно работать при решении задач. Это связано с тем, что высота совпадает с длиной бокового ребра. Последний факт облегчает процесс вычисления объема фигуры и площади ее боковой поверхности.
Видео:Основанием прямой треугольной призмы служит прямоугольный треугольник 8 ЗАДАНИЕ ЕГЭ МАТЕМАТИКА ПРОФИСкачать

Объем прямой призмы
Объем — свойственная любой пространственной фигуре величина, которая численно отражает часть пространства, заключенного между поверхностями рассматриваемого объекта. Объем призмы может быть рассчитан по следующей общей формуле:
То есть произведение высоты на площадь основания даст искомое значение V. Поскольку у прямой призмы основания равны, то для определения площади So можно брать любое из них.
Преимущество использования приведенной выше формулы именно для прямой призмы в сравнении с другими ее видами заключается в том, что высоту фигуры найти очень просто, так как она совпадает с длиной бокового ребра.
Видео:№235. Основанием прямой призмы является прямоугольный треугольник с острым углом φ. ЧерезСкачать
Площадь боковой поверхности
Удобно рассчитывать не только объем для прямой фигуры рассматриваемого класса, но также ее боковую поверхность. Действительно, любая ее боковая сторона — это либо прямоугольник, либо квадрат. Как вычислить площадь этих плоских фигур, знает каждый школьник, для этого необходимо умножить смежные стороны друг на друга.
Предположим, что в основании призмы лежит произвольный n-угольник, стороны которого равны ai. Индекс i пробегает значения от 1 до n. Площадь одного прямоугольника вычисляется так:
Площадь поверхности боковой Sb нетрудно вычислить, если сложить все площади Si прямоугольников. В таком случае получаем конечную формулу для Sb прямой призмы:
Sb = h*∑i=1n(ai) = h*Po.
Таким образом, чтобы определить площадь боковой поверхности для прямой призмы, необходимо умножить ее высоту на периметр одного основания.
Видео:№230. Основание прямой призмы — треугольник со сторонами 5 см и 3 см и углом, равным 120Скачать

Задача с треугольной призмой
Предположим, что задана прямая призма. Основание — прямоугольный треугольник. Катеты этого треугольника равны 12 см и 8 см. Необходимо рассчитать объем фигуры и ее полную площадь, если высота призмы составляет 15 см.
Для начала вычислим объем прямой призмы. Треугольник (прямоугольный), находящийся в ее основаниях, имеет площадь:
So = a1*a2/2 = 12*8/2 = 48 см2.
Как можно догадаться, a1 и a2 в этом равенстве являются катетами. Зная площадь основания и высоту (см. условие задачи), можно воспользоваться формулой для V:
V = So*h = 48*15 = 720 см3.
Полная площадь фигуры образована двумя частями: площадями оснований и боковой поверхностью. Площади двух оснований равны:
S2o = 2*So = 48*2 = 96 см2.
Для вычисления площади боковой поверхности необходимо знать периметр прямоугольного треугольника. Вычислим по теореме Пифагора его гипотенузу a3, имеем:
a3 = √(a12 + a22) = √(122 + 82) = 14,42 см.
Тогда периметр треугольника основания прямой призмы составит:
P = a1 + a2 + a3 = 12 + 8 + 14,42 = 34,42 см.
Применяя формулу для Sb, которая была записана в предыдущем пункте, получаем:
Sb = h*P = 15*34,42 = 516,3 см.
Сложив площади S2o и Sb, мы получим полную площадь поверхности изучаемой геометрической фигуры:
S = S2o + Sb = 96 + 516,3 = 612,3 см2.
Треугольная призма, которую изготавливают из специальных видов стекла, применяется в оптике при изучении спектров излучающих свет объектов. Такие призмы способны разлагать свет на составляющие частоты благодаря явлению дисперсии.
📹 Видео
Найдите объем треугольной призмыСкачать

Геометрия Основание прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12Скачать

Геометрия Основание прямой призмы – прямоугольный треугольник с катетами 15 см и 20 смСкачать

Геометрия Основанием прямой призмы ABCA1B1C1 является прямоугольный треугольник ABC, угол C = 90Скачать

Геометрия В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребраСкачать

Геометрия В основании прямой призмы лежит прямоугольный треугольник с острым углом 30Скачать

Стереометрия 5 | mathus.ru | высота призмы с прямоугольным треугольником в основанииСкачать

10 класс, 30 урок, ПризмаСкачать

11 класс, 31 урок, Объем прямой призмыСкачать

Геометрия Основание прямой призмы служит прямоугольный треугольник с острым углом 15. НаибольшаяСкачать

ПРЯМАЯ ПРИЗМА. ЕГЭ. ЗАДАНИЕ 5. СТЕРЕОМЕТРИЯСкачать

Г: Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 9 и 40 боковоеСкачать