Прямая имеет одну общую точку с окружностью если

Определение 1. Прямая, которая имеет с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

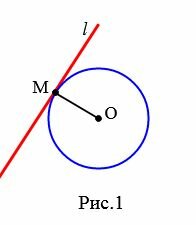
На рисунке 1 прямая l является касательной к окружности с центром O, а точка M является точкой касания прямой и окружности.

Свойство касательной

Теорема 1 (Теорема о свойстве касательной). Касательная к окружности перпендикулярна к радиусу, проведенному из центра окружности к точке касания прямой и окружности.

Доказательство. Пусть l касательная к окружности с центром O и M − точка касания прямой и окружности (Рис.1). Докажем, что ( small l ⊥ OM .)

Предположим, что радиус OM является наклонной к прямой l. Поскольку перпендикуляр, проведенной из точки O к прямой l меньше наклонной OM, от центра окружности до прямой l меньше радиуса окружности. Тогда прямая l и окружность имеют две общие точки (см. статью Взаимное расположение прямой и окружности). Но касательная не может иметь с окружностью две общие точки. Получили противоречие. Следовательно прямая l пенрпендикулярна к радиусу OM.

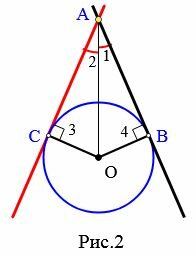
Рассмотрим две касательные к окружности с центром O, которые проходят через точку A и касаются окружности в точках B и C (Рис.2). Отрезки AB и AC называются отрезками касательных, проведенных из точки A.

Теорема 2. Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через данную точку и центр окружности.

Доказательство. Рассмотрим рисунок 2. По теореме 1 касательные AC и AB перпендикулярны радиусам OC и OB, соответственно. Тогда углы 3 и 4 прямые, а треугольники ACO и ABO, прямоугольные. Эти треугольники равны по катету (OC=OB) и гипотенузе (сторона AO− общая) (подробнее см. в статье Прямоугольный треугольник. Онлайн калькулятор). Тогда AB=AC и ( small angle 1=angle 2 .) Что и требовалось доказать.

Теорема, обратная теореме о свойстве касательной

Теорема 3. Если прямая проходит через конец радиуса, лежащей на окружности и перпенжикулярна к этому радиусу, то эта прямая является касательной.

Доказательство. По условию теоремы данный радиус является перпендикуляром от центра окружности к данной прямой. То есть расстояние от центра окружности до прямой равно радиусу окружности, и, следовательно, прямая и окружность имеют только одну общую точку (теорема 2 статьи Взаимное расположение прямой и окружности). Но это означает, что данная прямая является касательной к окружности (Определение 1).

Построение касательной к окружности

Задача 1. Через точку M окружности с центром O провести касательную этой окружности (Рис.3).

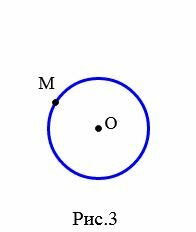Решение. Проведем прямую p через точки O и M. На прямой p из точки M отложим отрезок MN равной OM. Построим две окружности с центрами O и N и одинаковыми радиусами ON. Через точки пересечения этих окружностей проведем прямую l. Полученная прямая является касательным к окружности с центром O и радиусом OM.

Задача 2. Через точку A не принадлежащая к окружности с центром O провести касательную этой окружности (Рис.5).

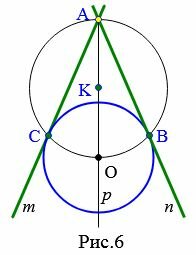Решение. Проведем прямую p через точки O и A (Рис.6). Найдем среднюю точку отрезка OA и обозначим буквой K. Постоим окружность с центром K радиусом KO=KA. Найдем точки пересечения этой окружности с окружностью с центром O. Получим точки B и C. Через точки A и C проведем прямую m. Через точки A и B проведем прямую n. Прямые m и n являются касательными к окружности с центром O.

Окружность. Касательная к окружности.

Прямая (MN), имеющая с окружностью только одну общую точку (A), называется касательной к окружности.

Общая точка называется в этом случае точкой касания.

Возможность существования касательной, и притом проведенной через любую точку окружности, как точку касания, доказывается следующей теоремой.

Теорема.

Если прямая перпендикулярна к радиусу в его конце, лежащем на окружности, то эта прямая — касательная.

Пусть O — центр некоторого круга и OA какой-нибудь его радиус. Через его конец A проведем MN ⊥ OA.Требуется доказать, что прямая MN — касательная, т.е. что эта прямая имеет с окружностью только одну общую точку A.

Допустим противное: пусть MN имеет с окружностью еще другую общую точку, например B. Тогда прямая OB была бы радиусом и, следовательно, равнялась бы OA.

Но этого быть не может, так как, если OA — перпендикуляр, то OB должна быть наклонной к MN, а наклонная больше перпендикуляра.

Обратная теорема.

Если прямая касательная к окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.

Следствие.

Через всякую данную на окружности точку можно провести касательную к этой окружности и притом только одну, так как через эту точку можно провести перпендикуляр, и притом только один, к радиусу, проведенному в нее.

Теорема.

Касательная параллельная хорде, делит в точке касания дугу, стягиваемую хордой, пополам.

Пусть прямая AB касается окружности в точке M и параллельна хорде СD. Требуется доказать, что ∪CM= ∪MD.

Проведя через точку касания диаметр ME, получаем: EM ⊥ AB и следовательно, EM ⊥ СD. Поэтому СM=MD.

Через данную точку провести касательную к данной окружности.

Если данная точка находится на окружности, то проводят через нее радиус и через конец радиуса перпендикулярную прямую. Эта прямая будет искомой касательной.

Рассмотрим тот случай, когда точка дана вне круга.

Пусть требуется провести к окружности с центром O касательную через точку A. Для этого из точки A, как из центра, описываем дугу радиусом AO, а из точки O, как центра, пересекаем эту дугу в точках B и С раствором циркуля, равным диаметру данного круга.

Проведя затем хорды OB и OС, соединим точку A с точками D и E, в которых эти хорды пересекаются с данной окружностью. Прямые AD и AE — касательные к окружности O. Действительно, из построения видно, что треугольники AOB и AOС равнобедренные (AO = AB =AС) с основаниями OB и OС, равными диаметру круга O.

Так как OD и OE — радиусы, то D — середина OB, а E — середина OС, значит AD и AE — медианы, проведенные к основаниям равнобедренных треугольников, и потому перпендикулярны к этим основаниям. Если же прямые DA и EA перпендикулярны к радиусам OD и OE, то они — касательные.

Следствие.

Две касательные, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей эту точку с центром.

Так AD=AE и ∠OAD = ∠OAE потому, что прямоугольные треугольники AOD и AOE, имеющие общую гипотенузу AO и равные катеты OD и OE (как радиусы), равны. Заметим, что здесь под словом “касательная” подразумевается собственно “отрезок касательной” от данной точки до точки касания.

Отрезки и прямые, связанные с окружностью. Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Свойства хорд и дуг окружности

Теоремы о длинах хорд, касательных и секущих

Доказательства теорем о длинах хорд, касательных и секущих

Теорема о бабочке

Отрезки и прямые, связанные с окружностью

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках

Фигура	Рисунок	Определение и свойства
Окружность
Круг
Радиус
Хорда
Диаметр
Касательная
Секущая

Окружность

Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Круг

Конечная часть плоскости, ограниченная окружностью

Радиус

Отрезок, соединяющий центр окружности с любой точкой окружности

Хорда

Отрезок, соединяющий две любые точки окружности

Диаметр

Хорда, проходящая через центр окружности.

Диаметр является самой длинной хордой окружности

Касательная

Прямая, имеющая с окружностью только одну общую точку.

Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Секущая

Прямая, пересекающая окружность в двух точках

Свойства хорд и дуг окружности

Фигура	Рисунок	Свойство
Диаметр, перпендикулярный к хорде		Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.
Диаметр, проходящий через середину хорды		Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.
Равные хорды		Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.
Хорды, равноудалённые от центра окружности		Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.
Две хорды разной длины		Большая из двух хорд расположена ближе к центру окружности.
Равные дуги		У равных дуг равны и хорды.
Параллельные хорды		Дуги, заключённые между параллельными хордами, равны.

Диаметр, перпендикулярный к хорде

Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Равные хорды

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Хорды, равноудалённые от центра окружности

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Две хорды разной длины

Большая из двух хорд расположена ближе к центру окружности.

Равные дуги

У равных дуг равны и хорды.

Параллельные хорды

Дуги, заключённые между параллельными хордами, равны.

Теоремы о длинах хорд, касательных и секущих

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Фигура	Рисунок	Теорема
Пересекающиеся хорды
Касательные, проведённые к окружности из одной точки
Касательная и секущая, проведённые к окружности из одной точки
Секущие, проведённые из одной точки вне круга

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Пересекающиеся хорды

Касательные, проведённые к окружности из одной точки

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Пересекающиеся хорды

Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Касательные, проведённые к окружности из одной точки

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.

Касательная и секущая, проведённые к окружности из одной точки

Секущие, проведённые из одной точки вне круга

Доказательства теорем о длинах хорд, касательных и секущих

Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).

Тогда справедливо равенство

Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).

Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство

Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство

откуда и вытекает требуемое утверждение.

Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).

Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство

Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).

Точка B – точка касания. В силу теоремы 2 справедливы равенства

откуда и вытекает требуемое утверждение.

Теорема о бабочке

Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.

Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:

Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим

Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим

Воспользовавшись теоремой 1, получим

Воспользовавшись равенствами (1) и (2), получим

Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство

откуда вытекает равенство

что и завершает доказательство теоремы о бабочке.

📸 Видео