На сторонах прямоугольного треугольника ABC, как на диаметрах, построены полуокружности w, w1 и w2. (рис.).
а) Докажите, что площадь треугольника ABC равна сумме площадей двух луночек, ограниченных полуокружностями w и w1 и полуокружностями w и w2.
б) Пусть прямая l касается w1 в точке M, а w2 в точке P. Найдите длину отрезка MP, если известно, что сумма площадей двух луночек равна 49.
а) Пусть AC = b, BC = a, AB = c. И пусть площадь луночки, ограниченной катетом b и дугой окружности ω будет равна D1, а площадь луночки ограниченной катетом a и дугой окружности ω будет равна D2. Тогда площадь треугольника ABC (обозначим SΔ) будет выражена так:
Найдем площадь S1 луночки, которая ограничена полуокружностями ω и ω1.
Аналогично найдем площадь S2 луночки, ограниченной полуокружностями ω и ω2, 
По теореме Пифагора: 
значит, 
(**)
Правые части равенств (*) и (**) совпадают, следовательно, обязаны совпасть и левые части, т. е. 
что и требовалось доказать.
Итак, MP 2 = 49, MP = 7.
Приведём другое решение:
а) Пусть AC = b, BC = a, AB = c. И пусть площадь луночки, ограниченной катетом b и полуокружностью ω, равна D1, катетом a и полуокружностью ω равна D2. Тогда
Правые части равенств (*) и (**) совпадают, следовательно, обязаны совпасть и левые части, т. е. 
что и требовалось доказать.
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Имеется верное доказательство утверждения пункта а и обоснованно получен верный ответ в пункте б. | 3 |
| Получен обоснованный ответ в пункте б. Имеется верное доказательство утверждения пункта а и при обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. | 2 |
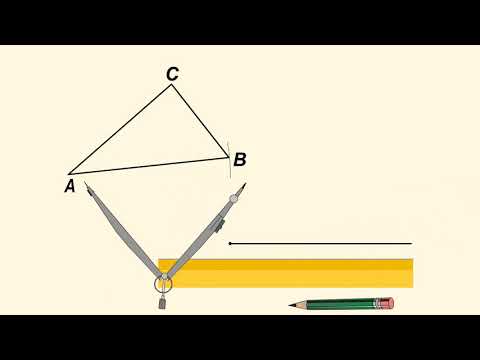
| Имеется верное доказательство утверждения пункта а. При обоснованном решении пункта б получен неверный ответ из-за арифметической ошибки. Содержание Видео:На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC Точка M — сереСкачать  На двух сторонах треугольника построили окружности§ 23. Метод геометрических мест точек в задачах на построение Известно, что если смешать синий и жёлтый цвета, то получим зелёный. Пусть на плоскости надо найти точки, обладающие какими-то двумя свойствами одновременно. Если синим цветом покрасить точки, обладающие первым свойством, а жёлтым — обладающие вторым свойством, то понятно, что зелёные точки будут обладать сразу двумя свойствами. В этом и состоит идея метода ГМТ, которую проиллюстрируем следующими задачами. Задача 1. Постройте треугольник по трём данным его сторонам.
Решение. Пусть даны три отрезка, длины которых равны a , b , c (рис. 327). Надо построить треугольник ABC , в котором AB = c , AC = b , BC = a . Проведём произвольную прямую. С помощью циркуля отложим на ней отрезок CB , равный a (рис. 328). Понятно, что задача свелась к построению третьей вершины треугольника, точки A . Воспользуемся тем, что точка A обладает сразу двумя свойствами:
1) принадлежит геометрическому месту точек, удалённых от точки B на расстояние c , т. е. окружности с центром в точке B радиуса с (см. рис. 328); 2) принадлежит геометрическому месту точек, равноудалённых от точки C на расстояние b , т. е. окружности с центром в точке С радиуса b (см. рис. 328). В качестве точки A можно выбрать любую из двух образовавшихся зелёных точек. Полученный треугольник ABC является искомым, так как в нём AB = c , AC = b , BC = a . Из описанного построения следует, что если каждый из трёх данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.
Задача 2. Постройте фигуру, все точки которой принадлежат данному углу, равноудалены от его сторон и находятся на заданном расстоянии a от его вершины. Решение. Искомые точки принадлежат сразу двум геометрическим местам точек: биссектрисе данного угла и окружности с центром в его вершине и радиусом, равным a . Построим биссектрису угла и указанную окружность (рис. 329). Их пересечением является искомая точка X . Задача 3. Постройте центр окружности радиуса R , проходящей через данную точку M и касающуюся данной прямой a . Решение. Поскольку окружность касается прямой a , то её центр находится на расстоянии R от этой прямой. Геометрическим местом точек, удалённых от данной прямой на данное расстояние, являются две параллельные прямые (см. упражнение 498). Следовательно, центр окружности находится на прямой b или на прямой с (рис. 330).
Геометрическое место точек, являющихся центрами окружностей радиуса R , проходящих через точку M , — это окружность данного радиуса с центром в точке M . Поэтому в качестве центра искомой окружности можно выбрать любую из точек пересечения окружности с одной из прямых b или с (рис. 331). Построение для случая, когда данная точка принадлежит данной прямой, рассмотрите самостоятельно. Задача 4. Постройте треугольник по стороне, медиане, проведённой к этой стороне, и радиусу описанной окружности.
Решение. Построим окружность данного радиуса и проведём хорду AB , равную стороне искомого треугольника. Тогда концы хорды являются двумя вершинами искомого треугольника. Понятно, что третья вершина принадлежит одновременно построенной окружности и окружности с центром в точке O , являющейся серединой хорды AB , и радиусом, равным данной медиане. Каждый из треугольников ABС 1 и ABС 2 (рис. 332) является искомым. Поскольку эти треугольники равны, то задача имеет единственное решение.
622. Даны прямая m и точки A и B вне её (рис. 333). Постройте на прямой m точку, равноудалённую от точек A и B . 623. Точки A и B принадлежат прямой m . Постройте точку, удалённую от прямой m на расстояние a и равноудалённую от точек A и B . Сколько решений имеет задача? 624. Точки B и C принадлежат разным сторонам угла A , причём АВ ≠ АС . Постройте точку M , принадлежащую углу, равноудалённую от его сторон и такую, что MB = MC . 625. Точки B и C принадлежат разным сторонам угла A . Постройте точку D , принадлежащую углу, равноудалённую от его сторон и такую, что DC = BC . Сколько решений может иметь задача? 626. Постройте равнобедренный треугольник по основанию и боковой стороне. 627. Для данной окружности постройте точку, являющуюся её центром. 628. Постройте окружность данного радиуса, проходящую через данную точку, центр которой принадлежит данной прямой. 629. Постройте окружность данного радиуса, проходящую через две данные точки. 630. Найдите все точки, принадлежащие данной окружности и равноудалённые от концов данного отрезка. Сколько решений может иметь задача? 631. Даны две пересекающиеся прямые m и n и отрезок AB . Постройте на прямой m точку, удалённую от прямой n на расстояние AB . Сколько решений имеет задача? 632. В треугольнике ABC известно, что ∠ C = 90°. На катете AC постройте точку D , удалённую от прямой AB на расстояние CD . 633. Постройте равнобедренный треугольник по основанию и радиусу описанной окружности. Сколько решений может иметь задача? 634. Постройте треугольник по двум сторонам и медиане, проведённой к одной из данных сторон. 635. Постройте равнобедренный треугольник по боковой стороне и медиане, проведённой к боковой стороне. 636. На данной окружности постройте точку, находящуюся на данном расстоянии от данной прямой. Сколько решений может иметь задача? 637. На данной окружности постройте точку, равноудалённую от двух данных пересекающихся прямых. Сколько решений может иметь задача? 638. Между двумя параллельными прямыми дана точка. Постройте окружность, проходящую через эту точку и касающуюся данных прямых. Сколько решений имеет задача? 639. Постройте окружность, проходящую через данную точку A и касающуюся данной прямой m в данной точке B . 640. Даны две параллельные прямые и секущая. Постройте окружность, касающуюся этих трёх прямых. 641. Постройте треугольник по двум сторонам и радиусу описанной окружности. Сколько решений может иметь задача? 642. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и радиусу описанной окружности. Сколько решений может иметь задача? 643. Постройте равносторонний треугольник по радиусу описанной окружности. 644. Три прямые попарно пересекаются и не проходят через одну точку. Постройте точку, равноудалённую от всех трёх прямых. Сколько решений имеет задача? 645. Постройте прямоугольный треугольник по катету и сумме гипотенузы и другого катета. 646. Постройте прямоугольный треугольник по гипотенузе и сумме катетов. 647. Постройте прямоугольный треугольник по гипотенузе и разности катетов. 648. Постройте прямоугольный треугольник по катету и разности гипотенузы и другого катета. 649. Постройте равнобедренный треугольник по основанию и разности боковой стороны и высоты, опущенной на основание. 650. Постройте треугольник по стороне, прилежащему к ней углу и сумме двух других сторон. 651. Постройте треугольник по стороне, прилежащему к ней углу и разности двух других сторон. 652. Постройте треугольник по стороне, противолежащему ей углу и разности двух других сторон. 653. Постройте треугольник по стороне, противолежащему ей углу и сумме двух других сторон. 654. Постройте треугольник по стороне, разности углов, прилежащих к этой стороне, и сумме двух других сторон. 655. Постройте треугольник по периметру и двум углам. 656. Постройте остроугольный треугольник по периметру, одному из углов и высоте, проведённой из вершины другого угла. 657. Постройте треугольник по высоте и медиане, проведённым из одной вершины, и радиусу описанной окружности. 658. Постройте треугольник по двум сторонам и медиане, проведённой к третьей стороне. 659. Постройте треугольник по стороне, высоте, проведённой к этой стороне, и медиане, проведённой к одной из двух других сторон. Упражнения для повторения
660. На рисунке 334 ∠ A = 46°, ∠ ACB = 68°, ∠ DEC = 120°. Найдите углы треугольников EFC и DBE . 661. Через середину O стороны MK треугольника MKN провели прямую, перпендикулярную стороне MK и пересекающую сторону MN в точке C . Известно, что MC = KN , ∠ N = 50°. Найдите угол MCO . 662. В треугольнике ABC из вершины прямого угла C провели высоту CH и биссектрису CM . Длина отрезка HM в 2 раза меньше длины отрезка CM . Найдите острые углы треугольника ABC . 663. На рисунке 335 BD = DC , DN ⊥ BC , ∠ BDM = ∠ MDA . Найдите сумму углов MBN и BMD . Наблюдайте, рисуйте, конструируйте, фантазируйте 664. Разрежьте фигуру, изображённую на рисунке 336, на три части, не являющиеся квадратами, так, чтобы из этих частей можно было сложить квадрат.
Когда сделаны уроки Из истории геометрических построений Умение достигать результат, используя минимальные средства, всегда считалось признаком высокого мастерства. Видимо, поэтому в Древней Греции в значительной степени было развито искусство выполнять геометрические построения с помощью только двух инструментов: дощечки с ровным краем (линейки) и двух заострённых палочек, связанных на одном конце (циркуля). Такое ограничение в выборе инструментов историки связывают с древнегреческой традицией, считавшей прямую и окружность самыми гармоничными фигурами. Так, в своей книге «Начала» великий учёный Евклид описывал построения геометрических фигур, при которых использовались лишь циркуль и линейка. Существует много задач на построение. С некоторыми из них вы уже успели познакомиться. Однако есть три задачи на построение, которые сыграли в развитии математики особую роль. Эти задачи стали знаменитыми. Задача о квадратуре круга. Построить квадрат, площадь которого равна площади данного круга. Задача о трисекции угла (от латинских tria — «три» и section — «разрезание») . Разделить угол на три равные части. Задача об удвоении куба. Построить куб, объём которого в 2 раза больше объёма данного куба. Эти задачи занимали умы людей на протяжении тысячелетий. Их пытались решить и такие выдающиеся учёные древности, как Гиппократ Хиосский, Евдокс Книдский, Евклид, Эратосфен, Аполлоний Пергский, Герон, Папп, Платон, Архимед, и гении Нового времени Рене Декарт, Франсуа Виет, Исаак Ньютон. И лишь в середине XIX века была доказана их неразрешимость, т. е. невозможность выполнить указанные построения с использованием лишь циркуля и линейки. Этот результат был получен средствами не геометрии, а алгебры, благодаря переводу этих задач на язык уравнений. Когда вы решали задачи на построение, особенно те, которые отмечены знаком В ХХ веке была обнаружена книга датского учёного Георга Мора (1640–1697), в которой он также описал построения одним циркулем. Поэтому сформулированную выше теорему называют теоремой Мора — Маскерони. Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать  Геометрические методы решения задач на построениеОбращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах. Видео:Строим вписанную в данный треугольник окружность (Задача 2).Скачать  «Снятие эмоционального напряжения |
, вы, по-видимому, испытали сложности, связанные с ограниченностью набора инструментов. Поэтому предложение ещё больше сузить возможности применяемых приборов может показаться вам по меньшей мере неожиданным. Однако ещё в Х веке персидский математик Мохаммед Абу-ль-Вефа описал решение целого ряда задач на построение с помощью линейки и циркуля, раствор которого нельзя было менять. Совсем удивительной является теорема, опубликованная в 1797 году итальянским математиком Лоренцо Маскерони (1750–1800): всякое построение, выполнимое циркулем и линейкой, можно проделать одним циркулем. При этом Маскерони обусловливал следующее: поскольку одним циркулем провести прямую нельзя, то прямая считается построенной, если построены какие-нибудь две её точки.
