Взаимное расположение прямой и окружности Выясним, сколько общих точек могут иметь прямая и окружность в зависимости от их взаимного расположения. Ясно, что если прямая проходит через центр окружности, то она пересекает окружность в двух концах диаметра, лежащего на. этой примой.
Пусть прямая р не проходит через центр О окружности радиуса r. Проведем перпендикуляр ОН к прямой р и обозначим буквой d длину этого перпендикуляра, т. е, расстояние от центра данной окружности до прямой (рис. 1). Исследуем взаимное расположение прямой и окружности в зависимости от соотношения между d и r. Возможны три случая.
1) d ОН= r (наклонная ОМ больше перпендикуляра ОН), и, следовательно , точка М не лежит на окружности. Итак, если расстояние от центра окружности до прямой равно радиусу то прямая и окружность имеют только одну общую точку.
3) d>r В этом случае -ОН> r поэтому .для любой точки М прямой р 0М
Мы доказали, что прямая и окружность могут иметь одну или две общие точки и могут не иметь ни одной общей точки. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. На рисунке 2 прямая р — касательная к окружности с центром О, А— точка касания.
Докажем теорему о свойстве касательной.
Теорема. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
Доказательство. Пусть р— касательная к окружности с центром О. А — точка касания (см. рис. 2). Докажем. что касательная р перпендикулярна к радиусу ОА.
Предположим, что это не так. Тогда радиус: ОА является наклонной к прямой р. Так как перпендикуляр, проведенный из точки О к прямой р, меньше наклонной ОА, то расстояния от центра О окружности до прямой р меньше радиуса. Следовательно, прямая р и окружность имеют две общие точки. Но это противоречит условию; прямая р — касательная. Таким образом, прямая р перпендикулярна к радиусу ОА. Теорема доказала.
Рассмотрим две касательные к окружности с центром О, проходящие через точку А и касающиеся окружности в точках В и С (рис. 3). Отрезки АВ и АС назовем отрезками касательных, проведенными из точки А. Они обладают следующим свойством, вытекающим из доказанной теоремы:
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Для доказательства этого утверждения обратимся к рисунку 3. По теореме о свойство касательной углы 1 и 2 прямые, поэтому треугольники АВО и АСО прямоугольные. Они равны, так как имеют общую гипотенузу ОА и равные катеты ОВ и ОС. Следовательно, АВ=АС и 

Теорема. Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Доказательство. Из условия теоремы следует, что данный радиус является перпендикуляром, проведенным из центра окружности к данной прямой. Поэтому расстояние от центра окружности до прямой равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку. Но это и означает, что данная прямая является касательной к окружности, Теорема доказана.
На этой теореме основано решение задач на построение касательной.
Прямая и окружность могут, очевидно, находиться только в следующих трех относительных положениях:
1) Расстояние (ОС) центра от прямой (АВ) (т. е, длина перпендикуляра ОС, опущенного из центра на прямую) больше радиуса окружности (рис. 1). Тогда точка С прямой удалена от центра больше, чем радиус, и потому лежит вне круга. Так как все остальные точки прямой удалены от О еще более, чем точка С (наклонные длиннее перпендикуляра), то они все лежат вне круга, значит, тогда прямая не имеет никаких точек, общих с окружностью.
2) Расстояние (ОС) центра от прямой меньше радиуса. В этом случае (рис.2) точка С лежит внутри круга и тогда, очевидно, прямая пересекается с окружностью.
3> Расстояние (ОС) центра от прямой равно радиусу. Тогда точна С (рис. 3) принадлежит и прямой, и окружности, все же остальные точки прямой, будучи удалены от О более, чем точка С, лежат вне круга. Значит, в этом случае Прямая и окружность имеют только одну общую точку, именно ту, которая служит основанием перпендикуляра, опущенного из центра на прямую.
Такая прямая, которая с окружностью имеет только одну общую точку, называется касательной к окружности; общая точка называется точкой касания.
Относительно касательной мы докажем следующие две теоремы (прямую и обратную) (рис. 4):
1) если прямая (MN) перпендикулярна к радиусу (ОА) в конце его (А), лежащем на окружности, то она касается окружности, и обратно (рис. 4);
2) если прямая касается окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.
1) Точка А, как конец радиуса, лежащий на окружности, принадлежит этой окружности; в то же время она принадлежит и прямой MN, Значит, эта точка есть общая у окружности и прямой. Все же остальные точки прямой MN, как В, С и другие, отстоят от центра О дальше, чем на радиус (так как отрезки ОВ, ОС, . как наклонные, больше перпендикуляра ОА), и потому они лежат вне окружности. Таким образом, у прямой MN есть только одна точка (А), общая с окружностью, и, значит, прямая MN есть касательная.
2) Если МN касается окружности в точке А, то все остальные точки этой прямой должны лежать вне окружности; вследствие этого отрезки ОВ, ОС, . больше радиуса ОА (точка О есть центр окружности). Значит, этот радиус есть наименьший из отрезков, соединяющих точку О с любой точкой прямой MN, и потому ОА | MN.
Теорема. Если касательная параллельна хорде, то точка касания делит дугу, стягиваемую хордой, пополам.
Пусть прямая АВ касается окружности в точке М (рис. 5) и параллельна хорде CD; требуется доказать, что 
Проведя через точку касания диаметр МЕ, будем иметь: 
Зависимость между дугами, хордами и расстояниями хорд от центра.
Теоремы. В одном круге или в равных кругах:
1) если дуги, равны, то стягивающие их хорды равны и одинаково удалены от центра;
2) если две дуги, меньшие полуокружности, не равны, то большая из них стягивается большей хордой и из обеих хорд большая расположена ближе к центру.
1) Пусть дуга АВ равна дуге CD (рис. 1), требуется доказать, что хорды АВ и CD равны, а также равны и перпендикуляры ОЕ и OF, опущенные из центра на хорды.
Повернем сектор OAJB вокруг центра О в направлении, указанном стрелкой на столько, чтобы радиус ОБ совпал с ОС. Тогда дуга ВА. пойдет по дуге CD и вследствие их равенства эти дуги совместятся. Значит, хорда AS совместится с хордой CD и перпендикуляр ОЕ совпадет с OF (из одной точки можно опустить на прямую только один перпендикуляр), т. е. AB=CD и OE=OF.
2) Пусть дуга АВ (рис. 2) меньше дуги CD, и притом обе дуги меньше полуокружности; требуется доказать, что хорда АВ меньше хорды CD, а перпендикуляр ОЕ больше перпендикуляра OF. Отложим на дуге CD дугу СК, равную АВ, и проведем вспомогательную хорду СК, которая, по доказанному, равна хорде АВ и одинаково с ней удалена от центра. У треугольников COD и СОК две стороны одного равны двум сторонам другого (как радиусы), а углы, заключенные между этими сторонами, не равны; в этом случае, как мы знаем, против большего из углов, т. е. lCOD, должна лежать большая сторона, значит, CD>CK, и потому CD>AB.
Для доказательства того, что OE>OF, проведем OLXCK и примем во внимание, что, по доказанному, OE=OL; следовательно, нам достаточно сравнить OF с OL. В прямоугольном треугольнике 0FM (покрытом на рисунке штрихами) гипотенуза ОМ больше катета OF; но OL>OM; значит, и подавно OL>OF. и потому OE>OF.
Теорема, доказанная нами для одного круга, остается верной и для равных кругов, потому что такие круги один от другого отличаются только положением.
Обратные теоремы. Так как в предыдущем параграфе рассмотрены всевозможные взаимно исключающие случаи относительно сравнительной величины двух дуг одного радиуса, причем получились взаимно исключающие выводы относительно сравнительной величины хорд и расстояний их от центра, то обратные предложения должны быть верны, в. именно:
В одном круге или е равных кругах:
1) равные хорды одинакова удалены от центра и стягивают равные дуги;
2) хорды, одинаково удаленные от центра, равны и стягивают равные дуги;
3) из двух неравных хорд большая ближе к центру и стягивает большую дугу;
4) из двух хорд, неодинаково удаленных от центра, которая ближе к центру, больше и стягивает большую дугу.
Эти предложения легко доказываются от противного. Например, для доказательства первого из них рассуждаем так: если бы данные хорды стягивали неравные дуги, то, согласно прямой теореме, они были бы не равны, что противоречит условию; значит, равные хорды должны стягивать равные дуги; а если дуги равны, то, согласно прямой теореме, стягивающие их хорды одинаково удалены от центра.
Теорема. Диаметр есть наибольшая из хорд.
Если соединим с центром О концы какой-нибудь хорды, не проходящей через центр, например хорды АВ (рис. 3) то получим треугольник АОВ, в котором одна сторона есть эта хорда, а две другие — радиусы, Но в треугольнике каждая сторона менее суммы двух других сторон; следовательно, хорда АВ менее суммы двух радиусов; тогда как всякий диаметр CD равен сумме двух радиусов. Значит, диаметр больше всякой хорды, не проходящей через центр. Но так как диаметр есть тоже хорда, то можно сказать, что диаметр есть наибольшая из хорд.
Как уже было сказано, отрезки касательных, проведенных к окружности из одной точки, имеют одинаковую длину. Эту длину называют касательным расстоянием от точки до окружности.
Без теоремы о касательных не обходиться решение не одной задачи о вписанных окружностях, иными словами, об окружностях, касающихся сторон многоугольника.
Касательные расстояния в треугольнике.
Найдем длины отрезков, на которые стороны треугольника АВС разбиваются точками касания с вписанной в него окружностью (рис. 1,а), например касательное расстояние tа от точки А до окружности. Сложим стороны b и c, а затем из суммы вычтем сторону а. Учитывая равенство касательных, проведенных из одной вершины, получим 2tа. Итак,
где p=(a+b+c)/2 – полупериметр данного треугольника. Длина отрезков сторон, прилегающим к вершинам В и С, равны соответственно p-b и p-c.
Аналогично, для вневписанной окружности треугольника, касающейся (снаружи) стороны а (рис. 1,б), касательные расстояния от В и С равны соответственно p-c и p-b, а от вершины А — просто p.
Заметим, что эти формулы можно использовать и «в обратную сторону».
Пусть в угол ВАС вписана окружность, причем касательное расстояние от вершины угла до окружности равно p или p-a, где p – полупериметр треугольника АВС, а а=ВС. Тогда окружность касается прямой ВС (соответственно снаружи или внутри треугольника).
В самом деле, пусть, например, касательное расстояние равно p-a. Тогда наши окружности касаются сторон угла в тех же самых точках, что и вписанная окружность треугольника АВС, а значит, совпадает с ней. Следовательно, она касается прямой ВС.
Описанный четырехугольник. Из теоремы о равенстве касательных сразу получается (рис. 2,а), что
если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны:
Отметим, что описанный четырехугольник обязательно выпуклый. Верно и обратное:
Если четырехугольник выпуклый и суммы его противоположных сторон равны, то в него можно вписать окружность.
Докажем это для четырехугольника, отличного от параллелограмма. Пусть какие-то две противоположные стороны четырехугольника, например AB и DC, при продолжении пересекутся в точке Е (рис. 2,б). Впишем окружность в треугольник ADE. Ее касательное расстояние te до точки E выражается формулой
Но по условию суммы противоположных сторон четырехугольника равны, а значит, AD+BC=AB+CD, или AD=AB+CD-BC. Подставив это значение в выражение для te, получим
а это – полупериметр треугольника BCE. Из доказанного выше условия касания следует, что наша окружность касается BC.
Две касательные, проведённые к окружности из точки вне её, равны и образуют равные углы с прямой, соединяющей эту точку с центром, что следует из равенства прямоугольных треугольников АОВ и АОВ1
- По условию задачи окружность и прямая ab имеют
- Окружность. Относительное взаимоположение окружностей.
- Отрезки и прямые, связанные с окружностью. Теорема о бабочке
- Отрезки и прямые, связанные с окружностью
- Свойства хорд и дуг окружности
- Теоремы о длинах хорд, касательных и секущих
- Доказательства теорем о длинах хорд, касательных и секущих
- Теорема о бабочке
- Презентация по геометрии «Решение задач повышенного уровня сложности по теме «Окружность» на ГИА»
- Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
- Описание презентации по отдельным слайдам:
- Прямая и окружность не имеют общих точек в задании
- 📹 Видео
Видео:Геометрия Окружности с центрами в точках O1 и O2 не имеют общих точек. Внутренняя общая касательнаяСкачать
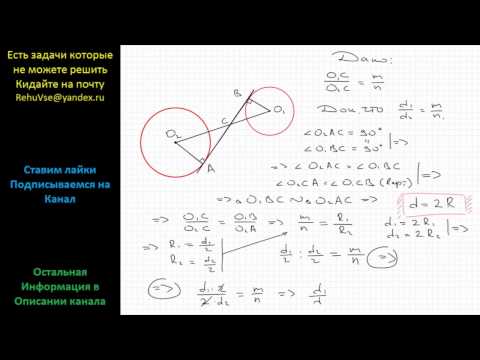
По условию задачи окружность и прямая ab имеют
Видео:Пойми Этот Урок Геометрии и получай 5-ки — Касательная и ОкружностьСкачать

Окружность. Относительное взаимоположение окружностей.
Если две окружности имеют только одну общую точку, то говорят, что они касаются.
Если же две окружности имеют две общие точки, то говорят, что они пересекаются.
Трех общих точек две не сливающиеся окружности иметь не могут, потому, что в противном случае через три точки можно было бы провести две различные окружности, что невозможно.
Будем называть линией центров прямую, проходящую через центры двух окружностей (например, прямую OO1).
Теорема.
Если две окружности имеют общую точку по одну сторону от линии центров, то они имеют общую точку и по другую сторону от этой линии, т.е. такие окружности пересекаются.
Пусть окружности O и O1 имеют общую точку A, лежащую вне линии центров OO1. Требуется доказать, что эти окружности имеют еще общую точку по другую сторону от прямой OO1.
Опустим из A на прямую OO1 перпендикуляр AB и продолжим его на расстояние BA1, равное AB. Докажем теперь, что точка A1 принадлежит обеим окружностям. Из построения видно, что точки O и O1 лежат на перпендикуляре, проведенном к отрезку AA1 через его середину. Из этого следует, что точка O одинаково удалена от A и A1. То же можно сказать и о точке O1. Значит обе окружности, при продолжении их, пройдут через A1.Таким образом, окружности имеют две общие точки : A (по условию) и A1 (по доказанному). Следовательно, они пересекаются.
Следствие.
Общая хорда (AA1) двух пересекающихся окружностей перпендикулярна к линии центров и делится ею пополам.
Теоремы.
1. Если две окружности имеют общую точку на линии их центров или на ее продолжении, то они касаются.
2. Обратно: если две окружности касаются, то общая их точка лежит на линии центров или на ее продолжении.
Признаки различных случаев относительного положения окружностей.
Пусть имеем две окружности с центрами O и O1, радиусами R и R1 и расстоянием между центрами d.
Эти окружности могут находиться в следующих 5-ти относительных положениях:
1. Окружности лежат одна вне другой, не касаясь. В этом случае, очевидно, d > R + R1 .
2. Окружности имеют внешнее касание. Тогда d = R + R1, так как точка касания лежит на линии центров O O1.
3. Окружности пересекаются. Тогда d R + R1, потому что в треугольнике OAO1 сторона OO1 меньше суммы, но больше разности двух других сторон.
4. Окружности имеют внутреннее касание. В этом случае в d = R — R1, потому что точка касания лежит на продолжении линии OO1.
5. Одна окружность лежит внутри другой, не касаясь. Тогда, очевидно,
d R + R1, то окружности расположены одна вне другой, не касаясь.
2. Если d = R + R1, то окружности касаются извне.
3. Если d R — R1, то окружности пересекаются.
4. Если d = R — R1, то окружности касаются изнутри.
5. Если d R Е R1. Значит, все эти случаи исключаются. Остается один возможный, именно тот, который требовалось доказать. Таким образом, перечисленные признаки различных случаев относительно положения двух окружностей не только необходимы, но и достаточны.
Видео:Прямая и окружность. Математика. 6 класс.Скачать

Отрезки и прямые, связанные с окружностью. Теорема о бабочке
 Отрезки и прямые, связанные с окружностью Отрезки и прямые, связанные с окружностью |
 Свойства хорд и дуг окружности Свойства хорд и дуг окружности |
 Теоремы о длинах хорд, касательных и секущих Теоремы о длинах хорд, касательных и секущих |
 Доказательства теорем о длинах хорд, касательных и секущих Доказательства теорем о длинах хорд, касательных и секущих |
 Теорема о бабочке Теорема о бабочке |
Видео:Взаимное расположение окружностей. Окружности не имеют общих точек.Скачать

Отрезки и прямые, связанные с окружностью
| Фигура | Рисунок | Определение и свойства |
| Окружность |  |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
| Окружность |
 |
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности

Конечная часть плоскости, ограниченная окружностью

Отрезок, соединяющий центр окружности с любой точкой окружности

Отрезок, соединяющий две любые точки окружности

Хорда, проходящая через центр окружности.
Диаметр является самой длинной хордой окружности

Прямая, имеющая с окружностью только одну общую точку.
Касательная перпендикулярна к радиусу окружности, проведённому в точку касания

Прямая, пересекающая окружность в двух точках
Видео:ОГЭ за одну минуту | ОГЭ, математика, задание 16 (окружность и касательная)Скачать

Свойства хорд и дуг окружности
| Фигура | Рисунок | Свойство |
| Диаметр, перпендикулярный к хорде |  | Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам. |
| Диаметр, проходящий через середину хорды | Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам. | |
| Равные хорды |  | Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности. |
| Хорды, равноудалённые от центра окружности | Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны. | |
| Две хорды разной длины |  | Большая из двух хорд расположена ближе к центру окружности. |
| Равные дуги |  | У равных дуг равны и хорды. |
| Параллельные хорды |  | Дуги, заключённые между параллельными хордами, равны. |
| Диаметр, перпендикулярный к хорде |
 |
Диаметр, перпендикулярный к хорде, делит эту хорду и стягиваемые ею две дуги пополам.

Диаметр, проходящий через середину хорды, перпендикулярен к этой хорде и делит стягиваемые ею две дуги пополам.

Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

Если хорды равноудалены (находятся на одном и том же расстоянии) от центра окружности, то они равны.

Большая из двух хорд расположена ближе к центру окружности.

У равных дуг равны и хорды.

Дуги, заключённые между параллельными хордами, равны.
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Теоремы о длинах хорд, касательных и секущих
| Фигура | Рисунок | Теорема |
| Пересекающиеся хорды |  |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:

Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.


| Пересекающиеся хорды | ||
 | ||
| Касательные, проведённые к окружности из одной точки | ||
 | ||
| Касательная и секущая, проведённые к окружности из одной точки | ||
 | ||
| Секущие, проведённые из одной точки вне круга | ||
 | ||
| Пересекающиеся хорды |
 |
Произведения длин отрезков, на которые разбита каждая из хорд, равны:
Если к окружности из одной точки проведены две касательных, то длины отрезков касательных от этой точки до точек касания с окружностью равны.
Видео:70. Взаимное расположение прямой и окружностиСкачать

Доказательства теорем о длинах хорд, касательных и секущих
Теорема 1 . Предположим, что хорды окружности AB и CD пересекаются в точке E (рис.1).
Тогда справедливо равенство
Доказательство . Заметим, что углы BCD и BAD равны как вписанные углы, опирающиеся на одну и ту же дугу. Углы BEC и AED равны как вертикальные. Поэтому треугольники BEC и AED подобны. Следовательно, справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 2 . Предположим, что из точки A , лежащей вне круга, к окружности проведены касательная AB и секущая AD (рис.2).
Точка B – точка касания с окружностью, точка C – вторая точка пересечения прямой AD с окружностью. Тогда справедливо равенство
Доказательство . Заметим, что угол ABC образован касательной AB и хордой BC , проходящей через точку касания B . Поэтому величина угла ABC равна половине угловой величины дуги BC . Поскольку угол BDC является вписанным углом, то величина угла BDC также равна половине угловой величины дуги BC . Следовательно, треугольники ABC и ABD подобны (угол A является общим, углы ABC и BDA равны). Поэтому справедливо равенство
откуда и вытекает требуемое утверждение.
Теорема 3 . Предположим, что из точки A , лежащей вне круга, к окружности проведены секущие AD и AF (рис.3).
Точки C и E – вторые точки пересечения секущих с окружностью. Тогда справедливо равенство
Доказательство . Проведём из точки A касательную AB к окружности (рис. 4).
Точка B – точка касания. В силу теоремы 2 справедливы равенства
откуда и вытекает требуемое утверждение.
Видео:Окружность и прямая: варианты взаимного расположенияСкачать

Теорема о бабочке
Теорема о бабочке . Через середину G хорды EF некоторой окружности проведены две произвольные хорды AB и CD этой окружности. Точки K и L – точки пересечения хорд AC и BD с хордой EF соответственно (рис.5). Тогда отрезки GK и GL равны.
Доказательство . Существует много доказательств этой теоремы. Изложим доказательство, основанное на теореме синусов, которое, на наш взгляд, является наиболее наглядным. Для этого заметим сначала, что вписанные углы A и D равны, поскольку опираются на одну и ту же дугу. По той же причине равны и вписанные углы C и B . Теперь введём следующие обозначения:
Воспользовавшись теоремой синусов, применённой к треугольнику CKG , получим
Воспользовавшись теоремой синусов, применённой к треугольнику AKG , получим
Воспользовавшись теоремой 1, получим
Воспользовавшись равенствами (1) и (2), получим
Проводя совершенно аналогичные рассуждения для треугольников BGL и DGL , получим равенство
откуда вытекает равенство
что и завершает доказательство теоремы о бабочке.
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Презентация по геометрии «Решение задач повышенного уровня сложности по теме «Окружность» на ГИА»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Видео:При каких значениях m прямая y = m не имеет с графиком ни одной общей точки.Скачать

Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Решение задач повышенного уровня сложности по теме «Окружность» на ГИА. Учитель математики МБОУ «Гимназия №2» Г. Курчатова Курской области Татаринова Людмила Николаевна.
Цель занятий: Совершенствование умения решать геометрические задачи. Подготовка к ГИА. Развитие интереса к изучению геометрии. Умение решать задачи… Искусство решать задачи… От чего оно зависит? Каждый из вас изучал много определений, аксиом, теорем о свойствах и признаках различных геометрических фигур. Так какие из них нужно отыскать в памяти при решении конкретной задачи? Какие действия следует выполнить, чтобы задача была решена? Сложность геометрических задач в том и состоит, что нет четких алгоритмов их решения. Кроме того, многие задачи могут быть решены разными способами.
Если вы хотите научиться решать геометрические задачи, то прежде всего необходимо систематизировать и обобщить знания по этому предмету. И только после большого количества самостоятельно решенных задач можно говорить о начале приобретения собственного опыта и формировании геометрической интуиции.
Необходимо научиться именно решать задачи, а не запоминать их решение. Известны такие высказывания : «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!» Д. Пойа. «Недостаточно лишь понять задачу, необходимо желание решить её. Без сильного желания решить трудную задачу невозможно, но при наличии такового возможно. Где есть желание, найдётся путь!» Д. Пойа
В известной книге Дьёрдь По́йа «Как решать задачу» автор предлагает следующий план решения задач: Нужно ясно понять задачу. Что дано? Что неизвестно? В чем состоит условие? Сделайте чертеж. Введите необходимые обозначения. Составьте план решения. Подумайте все ли данные вами использованы? Приняты ли во внимание все существенные понятия, содержащиеся в задаче? Осуществите план решения, контролируя каждый шаг, обосновывая каждый шаг, ссылаясь на известные определения, аксиомы, теоремы. Взгляд назад. Нужно изучить найденное решение.
Можно дополнительно дать еще такие советы. 1).Пусть при решении задачи вы пришли к необходимости нахождения длины отрезка. Следует подумать о том, чем может быть этот отрезок в других фигурах: медианой, биссектрисой, высотой, хордой, радиусом и так далее. 2).Если при решении задачи вы используете треугольник, то следует попытаться выяснить, не является ли он прямоугольным, равнобедренным или равносторонним.
На сегодняшнем занятии мы будем решать задачи типа №26 ГИА, взятые из банка задач ГИА на сайте ФИПИ или в диагностических работах системы «СтатГрад». Четких алгоритмов решения этих задач нет, но в некоторых задачах рассматривается повторяющаяся конфигурация. В процессе решения мы заодно будем повторять школьный курс планиметрии. Прочитав текст задачи, мы проанализируем ее и вспомним встретившиеся в условии понятия, свойства и признаки, которые будут использованы при решении данной задачи, а затем приступим к решению. Очень полезно составлять план решения. Следует проследить за цепочкой рассуждений, которая может привести к успеху.
Итак, наша первая задача: № 1. Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC. Прежде, чем приступать к решению задачи, вспомним определения, свойства и признаки, которые нам понадобятся.
Обзор теоретического материала по тексту задачи: 1) Медиана треугольника – отрезок, соединяющий вершину треугольника и середину противолежащей стороны. 2) Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
3) Вписанный угол, опирающийся на диаметр – прямой. 4) Если в треугольнике медиана совпадает с высотой, то этот треугольник является равнобедренным, а медиана проведена к основанию.
Определение: Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Если все вершины треугольника лежат на окружности, то окружность называется описанной около треугольника. Исходя из данных определений получаем, что все вершины вписанного треугольника равноудалены от центра окружности.
№ 1. Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC. Анализ условия. Зададим себе вопросы: 1.Сколько окружностей в условии задачи? Нужно ли изображать вторую окружность? 2.Где находится центр искомой окружности? 3. Как можно использовать данную медиану и середину стороны ВС? Нужны ли дополнительные построения? Известно, что центр окружности, описанной около треугольника есть точка пересечения серединных перпендикуляров к сторонам треугольника. Значит эти перпендикуляры проходят через точки М и К. Нужно ли их строить? Центр искомой окружности должен быть равноудален от вершин А, В, С. Есть ли на нашем чертеже такая точка? А В О М К С
№ 1. Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC. А В О М К С
Итак, взгляд назад. Повторим этапы решения задачи №1. 1) Угол ВКМ – прямой. 2)∆ ВМС равнобедренный. 3) МС = МВ = МА . М – центр окружности, АС = 6 диаметр. А В С М К
№ 2. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей. Обзор теоретического материала, необходимого при решении этой задачи. Проанализируем условие задачи и вспомним необходимые для ее решения свойства и признаки. Внешнее касание окружностей. 1. Точки А, В, С лежат на одной прямой. 2. АС = R + r. А В С R r
Теорема, обратная теореме Пифагора: Если в треугольнике квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный. Прямой угол лежит против большей стороны. а b с А В С
Вписанная в произвольный треугольник окружность a b c
№ 2. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей. Анализируем условие. А В С М К Р 10 2 2 3 3 10
№ 2. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей. Решение: Т.к. окружности касаются внешним образом, то АВ = АМ + МВ = 10 + 2 = 12 Аналогично ВС = 2+3=5, АС=10+3=13. А В С М К Р 10 2 2 3 3 10
Итак, повторим план решения задачи: А В С с b a
№ 3. Окружность радиуса 4 касается внешним образом второй окружности в точке М. Общая касательная к этим окружностям, проходящая через точку М, пересекается с некоторой другой их общей касательной в точке N . Найдите радиус второй окружности, если MN = 6 . В Е М N O A 6
№ 3. Окружность радиуса 4 касается внешним образом второй окружности в точке М. Общая касательная к этим окружностям, проходящая через точку М, пересекается с некоторой другой их общей касательной в точке N . Найдите радиус второй окружности, если MN = 6 . Обзор теоретического материала. Внешнее касание: 1.Три общие касательные: MN, AB, m. 2. Радиусы , проведенные в точку касания перпендикулярны касательной. 3. MN перпендикулярна ОЕ. 4. Изображая касательные, не забывайте Отмечать прямые углы и равные отрезки. 5. AN = NB = NM по свойству отрезков касательных. А В N M O E m
Биссектрисы смежных углов образуют прямой угол. 1 2 3 4
Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла. АО – биссектриса угла ВАС. АВ и АС касательные к окружности. Отрезки касательных из одной точки К одной окружности равны. АВ = АС. О В А С
Высота, прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между отрезками, на которые эта высота делит гипотенузу. h b a
№ 3. Окружность радиуса 4 касается внешним образом второй окружности в точке М. Общая касательная к этим окружностям, проходящая через точку М, пересекается с некоторой другой их общей касательной в точке N . Найдите радиус второй окружности, если MN = 6 . В Е М N O A 4 6
Высота, прямоугольного треугольника, проведенная к гипотенузе, есть среднее пропорциональное между отрезками, на которые эта высота делит гипотенузу. N О М Е 6 4 х
№ 3. Окружность радиуса 4 касается внешним образом второй окружности в точке М. Общая касательная к этим окружностям, проходящая через точку М, пересекается с некоторой другой их общей касательной в точке N . Найдите радиус второй окружности, если MN = 6 . В Е М N O A
Видео:Геометрия. 7 класс. Взаимное расположение прямой и окружности /13.04.2021/Скачать

Прямая и окружность не имеют общих точек в задании
Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.» — неверно, вписанные углы, опирающиеся на одну и ту же хорду окружности, равны, если их вершины лежат по одну сторону от хорды.
2) «Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.» — неверно, окружности имеют две общие точки.
3) «Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.» — верно, если расстояние от центра окружности до прямой меньше радиуса, то прямая и окружность имеют две общие точки.
4) «Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.» — верно, вписанный угол измеряется половиной дуги,на которую он опирается.
📹 Видео
ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Геометрия. ОГЭ по математике. Задание 16Скачать

Углы в окружности. 16 задание ОГЭ математика 2023 | Молодой РепетиторСкачать

Геометрия. ОГЭ по математике. Задание 16Скачать

9 класс, 8 урок, Взаимное расположение двух окружностейСкачать

8 класс, 31 урок, Взаимное расположение прямой и окружностиСкачать

№631. Пусть d — расстояние от центра окружности радиуса r до прямой р. Каково взаимное расположениеСкачать

ОГЭ по математике. Задание 16Скачать
















































